1P 2020 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (22 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 4: | Linje 4: | ||
[https://matematikk.net/matteprat/download/file.php?id=3096 løsning laget av Sander Syvertsen] | [https://matematikk.net/matteprat/download/file.php?id=3096 løsning laget av Sander Syvertsen] | ||
[https://matematikk.net/matteprat/download/file.php?id=3280 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | |||
[https://youtu.be/jWWDYvi58iw Videoløsning del 1 laget av Lektor Lainz] | |||
[https://youtu.be/tz5Hkvr9Y18 Videoløsning del 2 laget av Lektor Lainz] | |||
==DEL EN== | ==DEL EN== | ||
| Linje 182: | Linje 188: | ||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
Endeflaten er en halvsirkel med radius 7,5 cm og et rektangel med dimensjoner 18 cm x 15 cm. Arealet av en endeflate blir da: | |||
$A = b \cdot h + \frac 12 \pi \cdot r^2 = 15 cm \cdot 18 cm + \frac 12 \cdot \pi \cdot (7,5 cm) ^2 = 270 cm^2 + 88,4 cm^2 = 358,4 cm^2$ | |||
Vi multipliserer arealet av endestykket med lengden av postkassa, 40 cm, for å finne volumet: | |||
$V = A \cdot l = 358,4 cm^2 \cdot 40 cm =14336 cm^3 = 14,3 dm ^3 = 14,3 $ liter. | |||
===b)=== | |||
Vi fant den ene endeflaten i a. Det er en til, pluss bund, pluss langsider og tak. | |||
Endestykke x 2: $358,4 cm^2 \cdot 2 = 716,8 cm^2$ | |||
Bunn: $15 cm \cdot 40 cm = 600cm^2$ | |||
Langsider: $ 40 cm \cdot 18 cm \cdot 2 = 1440 cm^2 $ | |||
Arealet av taket er lengden av halvsirkelen multiplisert med lengden av postkassa: $7,5 \pi \cdot 40= 942,5$ | |||
Summen av disse flatene er overflatearealet av postkassa. Da har vi ikke tatt med det røde flagget som viser om det er post eller ikke. | |||
$O= 716,8cm^2 + 600cm^2 + 1440 cm^2 + 942,4cm^2 = 3699 cm^2 \approx 0,37 m^2$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
Ordinær lønn: $162 \cdot 130kr = 21060 kr$ | |||
40% overtid: $1,4 \cdot 14 \cdot 130kr = 2548kr$ | |||
100% overtid: $2 \cdot 7 \cdot 130kr = 1820 kr$ | |||
Brutto månedslønn blir summen av disse: 21 060 kr + 2 548 kr + 1 820 kr = 25 428 kr. | |||
===b)=== | |||
Feriepengegrunnlag = x : | |||
$x \cdot 0,12 = 8139 kr \\ x = \frac{8139 kr}{0,12} = 67 825kr $ | |||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 214: | Linje 263: | ||
Hun har nok maling til å male $5 m^2$. Arealet av figurene blir: | Hun har nok maling til å male $5 m^2$. Arealet av figurene blir: | ||
$16A = 16 \cdot ( \frac{4\pi - 3 \sqrt3}{6} 0,5^2 = 4,91$ | $16A = 16 \cdot ( \frac{4\pi - 3 \sqrt3}{6} )0,5^2 = 4,91$ | ||
Ja, hun har nok maling, dersom hun ikke søler mye. | Ja, hun har nok maling, dersom hun ikke søler mye. | ||
==Oppgave 8== | ==Oppgave 8== | ||
===a)=== | |||
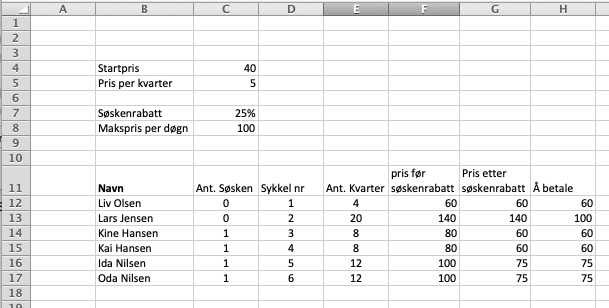
[[File: 1p-v2020-2-8ab.png ]] | |||
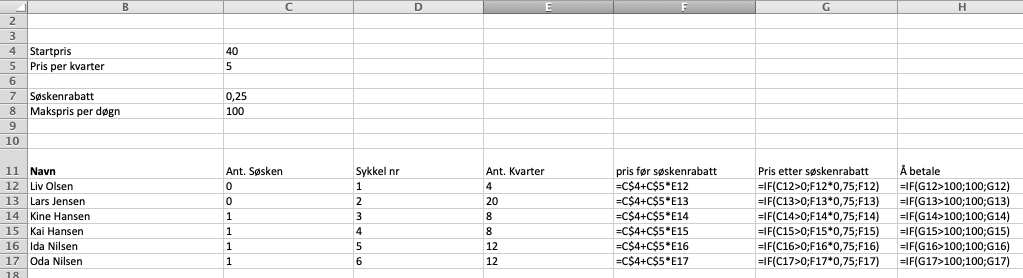
[[File: 1p-v2020-2-8abb.png ]] | |||
Tips: Se på formelen i F12. Ved å bruke <span>$</span> tegnet i cellereferansen låser man C4 og C5 slik at man kan kopiere hele kolonne F, fra F12 - F17. Dersom du skulle skrive alt ville det trolig ta 2-3 minutter. Å skrive C<span>$</span>4 og C<span>$</span>5 tar under ett sekund! Tid å spare her. | |||
===b)=== | |||
Fra figuren i a ser man at de må betale to ganger 75 kr, 150 kroner tilsammen. | |||
Siste sideversjon per 18. nov. 2020 kl. 22:47
Diskusjon av denne oppgaven på matteprat
løsning laget av Sander Syvertsen
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsning del 1 laget av Lektor Lainz
Videoløsning del 2 laget av Lektor Lainz
DEL EN
Oppgave 1
Det minste kvadratet må ha sider lik AC = 9 dm. Da blir arealet av kvadratet utspent av hypotenusen, det største, lik:
$(BC)^2 = 81dm^2 + (12dm)^2 = 81dm^2 + 144dm^2 =225dm^2$
Oppgave 2
Varene koster 230 kr. Vi vet at mva er 15% av det varene koster uten mva. Dersom vi tenker at prisen uten mva er 100%, betaler vi 230kr som er 115%. Vi bruker vekstfaktor og finner prisen uten mva:
$230 kr : 1,15 = 23000kr : 115 =200 $
Altså betaler vi 30 kr i mva.
Oppgave 3
Målestokk er modell delt på virkelighet. Vi må huske samme benevning på begge.
$\frac{5 cm}{2,5 km} = \frac{5cm}{250000cm} = \frac{1}{50000}$, eller 1 : 50 000 som man vanligvis skriver. Det betyr at 1 cm på kartet er 500 meter i virkeligheten.
Oppgave 4
Vinkel A og D er rette. Vinkel B er felles i begge trekantene, derfor er de formlike. Forholdet mellom lengdene i trekantene er $\frac{DE}{AC} = 0,6$. Lengden av DB blir da
$DB= 0,6AB =0,6 \cdot 15cm = 9 cm$
Oppgave 5
"Blandingen" består av 7 deler i forholdet 3 : 4. En "del" er da 4 kuler. Det betyr at $4 \cdot 3 = 12$ er røde og at 16 er hvite.
Oppgave 6
a)
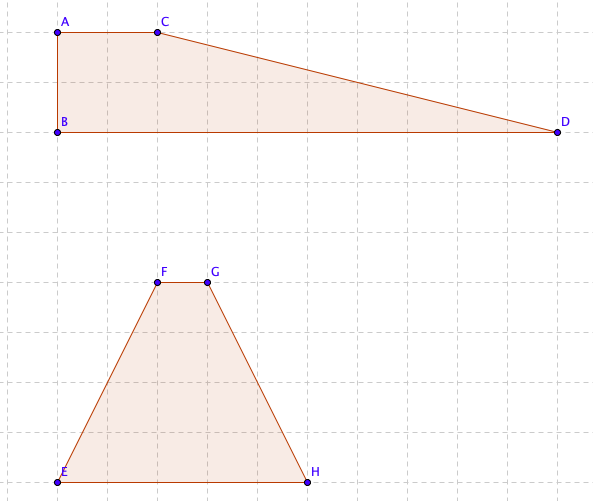
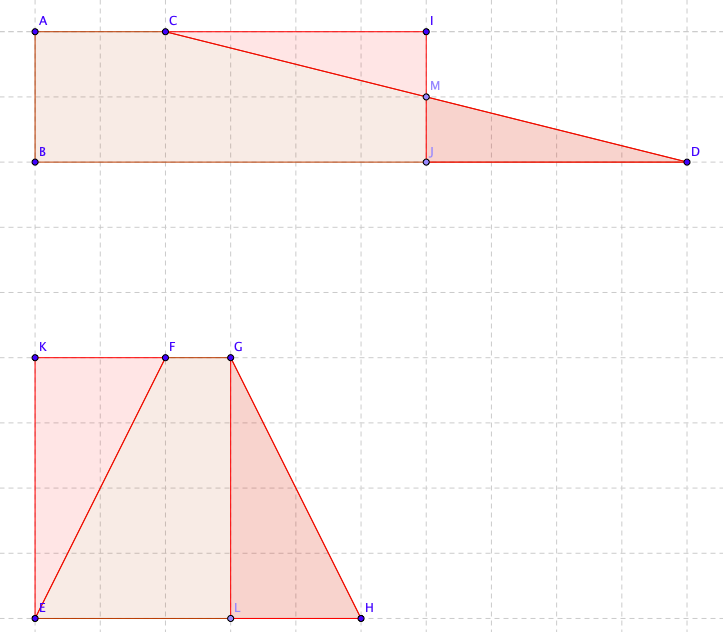
Arealet av et trapes er gjennomsnittet av de parallelle sidene, ganget med avstanden mellom dem. Hvorfor det er slik er vist grafisk her:
Man lager rektangler av trapesene.
Arealet av det første blir $A1 = \frac {BD + AC}{2} \cdot h$
der h er avstanden mellom de parallelle linjene. Vi får da
$A1 = \frac {10 + 2}{2} \cdot 2 = 12$
Og tilsvarende på det andre:
$A2 = \frac{1+5}{2} \cdot 4 = 12$
b)
Fra formelen i a ser man at når lengden av sidene øker må avstanden mellom de parallelle linjene bli mindre, dersom arealet skal være konstant.
$A = \frac{s\cdot h}{2} \\ 12=\frac{s\cdot h}{2} \\ s \cdot h = 24$
Vi ser at s ganger h er konstant, og de er dermed omvendt proporsjonale størrelser.
Vi kan skrive forholdet mellom s og h som $s = \frac{24}{h}$
eller $h= \frac{24}{s}$, når arealet av trapeset er 12.
Oppgave 7
Det er 10 mulige tall på hver sifferplass, altså er sannsynligheten 1/10 for et spesielt tall. Vi bruker multiplikasjonsprinsippet og får:
$P(2 4 \quad eller \quad 42) = P( 2 4 ) + P ( 4 2) = \frac{1}{10} \cdot \frac{1}{10} + \frac{1}{10} \cdot \frac{1}{10} = \frac {2}{100} = \frac{1}{50}$
Oppgave 8
Reallønn = REA
Nominell lønn =NOM
Vi har at:
$\frac{REA}{100} = \frac{NOM}{KPI} \\ \frac{1000000}{100} = \frac{NOM}{105,5} \\ NOM = \frac{1000000 \cdot 105,5}{100} = 1055000$
Oppgave 9
Lengden av sidene i kvadratet er lik diameter som er 2r, 14dm. Kvadratdelen av vinduet består av tre sider blir da 42 dm.
Omkretsen av en sirkel er $O= 2 \pi r$ Vi skal bare ha en halvsirkel : $ \pi \cdot r = \frac{22}{7} \cdot 7 dm = 22 dm$.
Summen av disse lengdene blir 64 dm, som er den omtrentlige omkretsen av vinduet.
Oppgave 10
a)
Se figur over. Du må bruke linjal og tegne for hånd.
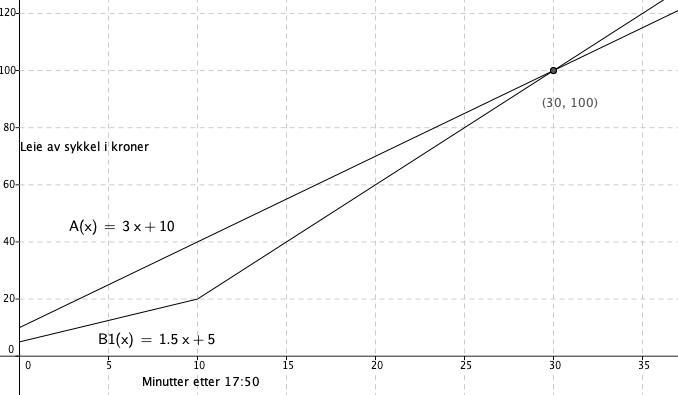
b)
Fra figuren ser man at tilbudene er økonomisk like etter 30 minutter. Da er prisen for begge 100 kroner. Dersom hun leier sykkel lengre enn en halv time er tilbud A rimeligst.
DEL TO
Oppgave 1
a)
b)
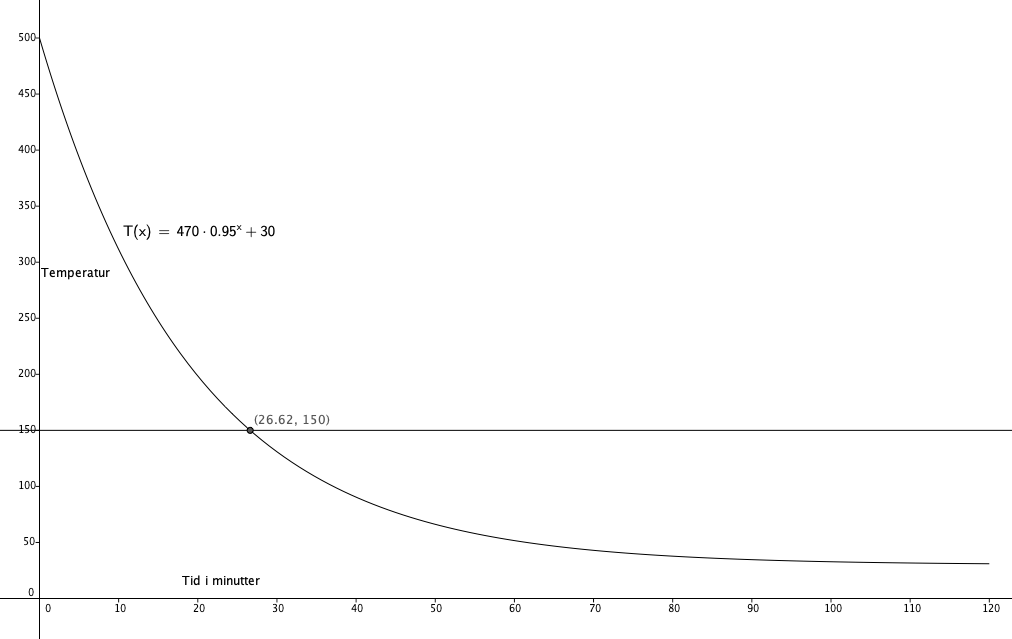
Det var 500 grader.
c)
Fra grafen ser man at man har ca 26,5 minutter til bearbeiding.
Oppgave 2
a)
Maskin A produserer 200 låser, og maskin B 100 låser. 5% av 200 er 10, og 2% av 100 er 2. Vi får følgende tabell:
| A | B | Sum | |
| FEIL | $ 10$ | $ 2$ | 12 |
| IKKE FEIL | $190$ | $98$ | 288 |
| Sum | 200 | 100 | 300 |
b)
Det er 12 låser med feil, av 300:
$\frac{12}{300} \cdot 100$% = 4%
Det er 4% sannsynlig at man trekker en med feil.
c)
Av 12 låser med feil er 10 produsert på maskin A:
$\frac{10}{12} \cdot 100$% =83,3%
Oppgave 3
Man må finne ut hvor mange minutter det er i et år:
$60 \cdot 24 \cdot 365 = 525600$
Vi deler så antall tonn på antall minutter:
8 000 000 tonn : 525 600 minutter = 15,2 tonn / minutt.
Oppgave 4
a)
Endeflaten er en halvsirkel med radius 7,5 cm og et rektangel med dimensjoner 18 cm x 15 cm. Arealet av en endeflate blir da:
$A = b \cdot h + \frac 12 \pi \cdot r^2 = 15 cm \cdot 18 cm + \frac 12 \cdot \pi \cdot (7,5 cm) ^2 = 270 cm^2 + 88,4 cm^2 = 358,4 cm^2$
Vi multipliserer arealet av endestykket med lengden av postkassa, 40 cm, for å finne volumet:
$V = A \cdot l = 358,4 cm^2 \cdot 40 cm =14336 cm^3 = 14,3 dm ^3 = 14,3 $ liter.
b)
Vi fant den ene endeflaten i a. Det er en til, pluss bund, pluss langsider og tak.
Endestykke x 2: $358,4 cm^2 \cdot 2 = 716,8 cm^2$
Bunn: $15 cm \cdot 40 cm = 600cm^2$
Langsider: $ 40 cm \cdot 18 cm \cdot 2 = 1440 cm^2 $
Arealet av taket er lengden av halvsirkelen multiplisert med lengden av postkassa: $7,5 \pi \cdot 40= 942,5$
Summen av disse flatene er overflatearealet av postkassa. Da har vi ikke tatt med det røde flagget som viser om det er post eller ikke.
$O= 716,8cm^2 + 600cm^2 + 1440 cm^2 + 942,4cm^2 = 3699 cm^2 \approx 0,37 m^2$
Oppgave 5
a)
Ordinær lønn: $162 \cdot 130kr = 21060 kr$
40% overtid: $1,4 \cdot 14 \cdot 130kr = 2548kr$
100% overtid: $2 \cdot 7 \cdot 130kr = 1820 kr$
Brutto månedslønn blir summen av disse: 21 060 kr + 2 548 kr + 1 820 kr = 25 428 kr.
b)
Feriepengegrunnlag = x :
$x \cdot 0,12 = 8139 kr \\ x = \frac{8139 kr}{0,12} = 67 825kr $
Oppgave 6
a)
Når noe vokser med en fast prosent hver tidsperiode har man eksponentiell vekst. Vekstfaktoren er 1,035. Startverdien er 810 000 kr. og tidsperiodene er 10:
Om 10 år$ = 810000 \cdot 1,035^{10}$ kr = 1 142 585 kr på konto.
b)
For 5 år siden var det x kroner på konto. I dag er det 810 000 kroner. Renten er den samme og tiden er 5 år. Vi setter opp likningen:
$ x \cdot 1,035^5 = 810000kr \\ x = 1,035^{-5} \cdot 810000 kr = 681998,27 kr$
Oppgave 7
a)
Avstanden mellom D, B og C er alle en radius. Det samme med A, B og D. Årsaken til det er at punktene ligger enten på sikelpereferier (A og C) eller i sentrum og på sirkelfereferier (B og D). Begge sirkler har radus r, altså er avstanden mellom alle punktene r.
b)
Trekantene ABD og BCD er likesidede og vinklene er 60 grader. Vinkel A og vinkel C er da 60 grader, mens vinkel D og vinkel B er 120 grader.
c)
Hun har nok maling til å male $5 m^2$. Arealet av figurene blir:
$16A = 16 \cdot ( \frac{4\pi - 3 \sqrt3}{6} )0,5^2 = 4,91$
Ja, hun har nok maling, dersom hun ikke søler mye.
Oppgave 8
a)
Tips: Se på formelen i F12. Ved å bruke $ tegnet i cellereferansen låser man C4 og C5 slik at man kan kopiere hele kolonne F, fra F12 - F17. Dersom du skulle skrive alt ville det trolig ta 2-3 minutter. Å skrive C$4 og C$5 tar under ett sekund! Tid å spare her.
b)
Fra figuren i a ser man at de må betale to ganger 75 kr, 150 kroner tilsammen.