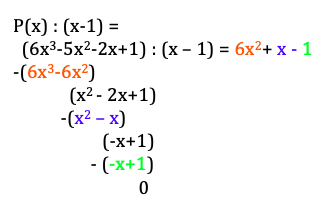R1 2020 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| (118 mellomliggende versjoner av 6 brukere er ikke vist) | |||
| Linje 4: | Linje 4: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=51506&start=45#p238234 Løsningsforslag til del 1 av Kristian Saug] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=51506&start=45#p238234 Løsningsforslag til del 1 av Kristian Saug] | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=51506&start=45#p238262 Løsningsforslag del 2 av Kristian Saug] | |||
[https://udl.no/p/r1-matematikk/r1-eksamen-var-2020 Video-løsninger av UDL.no] | |||
[https://matematikk.net/matteprat/download/file.php?id=3119 Løsningsforslag av Svein Arneson] | |||
[https://matematikk.net/matteprat/download/file.php?id=4014 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | |||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHWcQGvwbL3hrC7W4DCMx1i4 Videoløsninger til del 1 laget av Lektor Håkon Raustøl] | |||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHVthlz3_Jv43ChBpZzzkD8l Videoløsninger til del 2 laget av Lektor Håkon Raustøl] | |||
[https://youtu.be/9LfU3Msvhu0 Løsningsforslag del 1 video av Lektor Lainz] | |||
[https://youtu.be/6mojzWU2tZ4 Løsningsforslag del 2 video av Lektor Lainz] | |||
==Oppgave 1== | |||
===a)=== | |||
$f(x)=x^6 + 3x^5 + ln(x) \\ f'(x)= 6x^5+15x^4 + \frac{1}{x}$ | |||
===b)=== | |||
$g(x)=2x^2 \cdot e^{2x-1}\\ g'(x) = 4x \cdot e^{2x-1} + 2x^2 \cdot 2 \cdot e^{2x-1} = (1+x)4x \cdot e^{2x-1}$ | |||
===c)=== | |||
$h(x) = \frac{4x-1}{x+2} \\ h'(x) = \frac{4(x+2) - (4x-1)}{(x+2)^2} = \frac{9}{(x+2)^2}$ | |||
==Oppgave 2== | |||
===a)=== | |||
$ln(x^2) + ln(x) = 12 \\ 2 ln(x) + ln(x) = 12 \\ 3 ln(x) = 12 \\ e^{ln(x)} = e^4 \\ x = e^4 $ | |||
===b)=== | |||
$e^{2x}-e^x =6 \\(e^x)^2 - e^x - 6 =0 \\ u = e^x \\ u^2-u-6=0 \\ u = 3 \vee u = -2 \\ e^x = 3 \vee e^x = -2 \\ x = ln(3)$ | |||
$e^x =-2$ har ingen løsning. | |||
==Oppgave 3== | |||
$\vec{u} \cdot \vec{v } =-2$ og $|\vec u | = 3$ og $ |\vec v | = 2$ | |||
$\vec a = 2 \vec u + 3 \vec v$ og $ \vec b = t \cdot \vec u + 5 \vec v$ | |||
===a)=== | |||
Dersom to vektorer er parallelle: | |||
$ k \vec{a} = \vec{b} \\ k(2 \vec u + 3 \vec v) = t \cdot \vec u + 5 \vec v \\ 2k \vec u = t \cdot u \wedge 3k \cdot \vec v = 5 \vec v \\ t = 2k \wedge k = \frac 53 \\ t = \frac{10}{3}$ | |||
===b)=== | |||
Når to vektorer står normalt på hverandre er skalarproduktet null: | |||
$ (2 \vec{ u} + 3 \vec {v})(t \cdot \vec u + 5 \vec v )= 0 \\ 2 \cdot t \cdot \vec {u^2} + 10 \cdot \vec{ u} \cdot \vec v + 3 \cdot t \cdot \vec u \cdot \vec v + 15 \vec{ v^2}$ | |||
Fra oppgaveteksten vet vi at: $\vec{u^2} = | \vec {u} | \cdot |\vec {u} | =9 \\ \vec{v^2} = | \vec{v} | \cdot | \vec{v} | = 4 \\ \vec{u} \cdot \vec{v} = -2$ | |||
Setter inn og får: | |||
$2 \cdot t \cdot 9 +10 \cdot (-2) + 3 \cdot t \cdot(-2) + 15 \cdot 4 =0 \\ 12t = -40 \\ t = - \frac{10}{3}$ | |||
==Oppgave 4== | |||
===a)=== | |||
Dersom polynomet går opp i (x-1) må P(1) være lik null: | |||
$P(1) = 6 \cdot 1^3-5 \cdot 1^2-2 \cdot 1 +1 = 6-5 -2+1=0$, altså går divisjonen P(x) : (x-1) opp. | |||
===b)=== | |||
[[File: r1-v2020-1-4b.png ]] | |||
Faktoriserer så $6x^2+x-1$: | |||
$x= \frac{-1 \pm \sqrt{1-4 \cdot 6 \cdot (-1)}}{12} =\frac{-1 \pm 5}{12} \\ x = - \frac 12 \vee x= \frac 13 $ | |||
$6x^2+ x -1 = 6(x + \frac 12)(x - \frac 13) = (2x+1)(3x-1)$ | |||
Altså kan man skrive: | |||
$P(x)= (x-1)(2x+1)(3x-1)$ | |||
===c)=== | |||
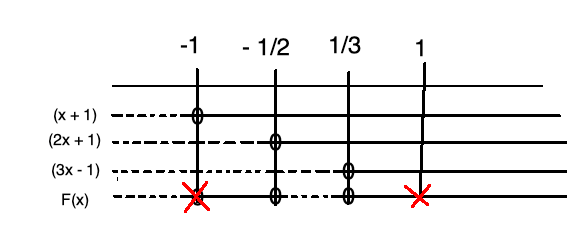
$F(x) = \frac{P(x)}{(x^2-1)} = \frac{(2x+1)(3x-1)}{(x+1)}$ | |||
Nå må vi huske at nevneren fører til at F(x) ikke er definert for x = -1 eller for x = 1. | |||
Setter inn i et fortegnsskjema, for å drøfte fortegnet til F(x): | |||
[[File: r1-v2020-2-1-4c2.png ]] | |||
Vi får tre områder der F er større eller lik null: | |||
$x \in < -1, - \frac 12] \cup [ \frac 13 , 1> \cup < 1, \rightarrow>$ | |||
===d)=== | |||
$P(x)= (x-1)(2x+1)(3x-1)$ og $F(x)= \frac{P(x)}{x^2-1} = \frac{(x-1)(2x+1)(3x-1)}{(x+1)(x-1)} = \frac{(2x+1)(3x-1)}{(x+1)}$ | |||
$\lim\limits_{x \to 1} F(x) = \frac{(2 \cdot 1+1)(3 \cdot 1-1)}{(1+1)} = \frac 62 =3$ | |||
$\lim\limits_{x \to -1} F(x) = \frac{(2 \cdot -1+1)(3 \cdot -1-1)}{(-1+1)} = $ | |||
Når x går mot -1 går telleren mot 4 og nevneren mot 0. Grensen eksisterer ikke. | |||
==Oppgave 5== | |||
===a)=== | |||
Vi velger 3 av 8 bøker. Rekkefølgen vi trekker i har ikke betydning. Hvor mange kombinasjoner finnes? : | |||
$3C8 = \frac{8!}{5! \cdot 3!} = \frac {8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} = 8 \cdot 7 = 56$ | |||
Det er mulig å velge 56 kombinasjoner av bøker. | |||
===b)=== | |||
Dette er en hypergeometrisk situasjon. Vi trekker 4 og 3 skal være riktige: | |||
$\frac{\binom{3}{3} \binom{5}{1}}{ \binom{8}{4}} = \frac{1 \cdot 5 }{70} = \frac {1}{14} $ | |||
===c)=== | |||
Det "motsatte" av minst to er null og en; dersom drikke får minst to, får du enten null eller en. | |||
Vi finner P (minst to bøker) = 1 - ( P( null bøker) + P( en bok) ) | |||
På matematikkspråk er dette sannsynligheten av komplementære hendelser, og ikke "motsatte" som vi skrev over. | |||
$P(x=0) = \frac{\binom{3}{0} \binom{5}{4}}{ \binom{8}{4}} = \frac{1 \cdot 5 }{70} = \frac {1}{14} $ | |||
$P(x=1) = \frac{\binom{3}{1} \binom{5}{3}}{ \binom{8}{4}} = \frac{1 \cdot 5 }{70} = \frac {3}{7} $ | |||
Vi får da P( minst to riktige bøker) = $1- \frac {1}{14} - \frac 37 = 0,5$ , altså 50 % sjanse for minst to riktige. | |||
Vi kunne også ha regnet ut sannsynligheten for to riktige og lagt det til sannsynligheten for tre, som vi regnet ut i b, kanskje litt tidsbesparende. | |||
==Oppgave 6== | |||
===a)=== | |||
AB har lengden 6 og DC har lengden 2x. Høyden er f(x): | |||
$F(x) = \frac{6+2x}{2} \cdot (9-x^2) = -x^3 - 3x^2 +9x+ 27$ | |||
===b)=== | |||
$F'(x) = -3x^2-6x+9$ | |||
$F'(x) = 0 $ gir x= -3 eller x = 1. | |||
Av uttrykket for den deriverte ser man at den deriverte går fra positv til negativ i nullpunktet x = 1 ( parabelen vender sin hule side ned.) | |||
$F(1)= -1-3 + 9 + 27 = 32$ | |||
Størst areal er 32, når x = 1. | |||
==Oppgave 7== | |||
Vinkel D er 65 grader, da er vinkel w = 130 grader. (periferi / sentral vinkel) Av samme grunn er u = 65 grader. I trekanten BCE er vinkelen i E (180-35-65) grader = 80 grader. Det gjør at vinkel v = 100 grader. | |||
==Oppgave 8== | |||
===a)=== | |||
Linjen l har parameterfremstilling: | |||
$ l: \left\{ \begin{array}{rcl} x=t \\ y=2t+1 \end{array}\right. $ | |||
For en vilkårlig t verdi er D (t, 2t + 1) | |||
$\vec{AD} = [ t - (-1), (2t+1) - 1 ] = [ t+1 , 2t]$, som skulle vises. | |||
===b)=== | |||
$\vec{AD} = [t+1, 2t ]$ og $\vec {CD} = [t-7, 2t - 4]$ | |||
Lengden av AD og CD vektor skal være like. | |||
$|\vec{AD}|^2 = |\vec{CD}|^2 \\ (t+1)^2+ 4t^2 = (t-7)^2 + (2t-4)^2 \\ t^2+2t+1+4t^2 = t^2-14t+49+4t^2-16t+16 \\32t =64 \\ t=2 $ | |||
Som innsatt gir D (2, 5) | |||
Koordinatene til punkt B: | |||
$\vec{OB} = \vec{OA} + \vec{AB} = \vec{OA} - \vec {CD} = [-1, 1] - [-5, 0] = [4, 1]$ | |||
Punktet B har koordinatene (4, 1). | |||
==DEL TO== | |||
==Oppgave 1== | |||
===a)=== | |||
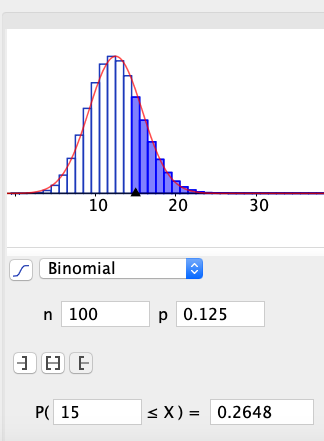
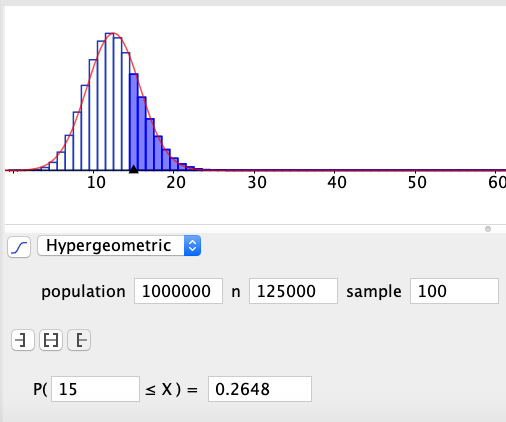
Situasjonen er i utgangspunktet hypergeometrisk. | |||
For å kunne regne binomisk: | |||
Tellingen av en bil skal ikke påvirke den neste. Dersom hun teller bilene i en "elbil kortesje" blir det feil. Hun må anta at populasjonen av biler er stor i forhold til de 100 hun teller, slik at det ikke endrer sannsynligheten (man kan tenke at å telle en bil er det samme som å trekke ut, uten tilbakelegging. Dersom populasjonen er stor i forhold til utvalget vil ikke sannsynligheten påvirkes i nevneverdig grad.) | |||
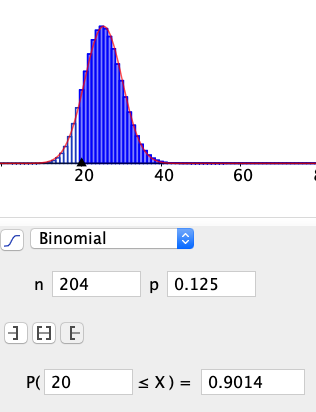
===b)=== | |||
[[ File:r1-v2020-2-1b1.png]] | |||
[[ File:r1-v2020-2-1b2.png]] | |||
===c)=== | |||
[[ File:r1-v2020-2-1c.png]] | |||
==Oppgave 2== | |||
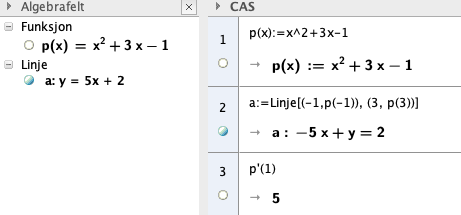
===a)=== | |||
[[ File:r1-v2020-2-2a.png]] | |||
Begge linjene har stigningstall 5, altså er de parallelle. | |||
===b)=== | |||
[[File: r1-v2020-2-2b.png ]] | |||
Som skulle vises. | |||
==Oppgave 3== | |||
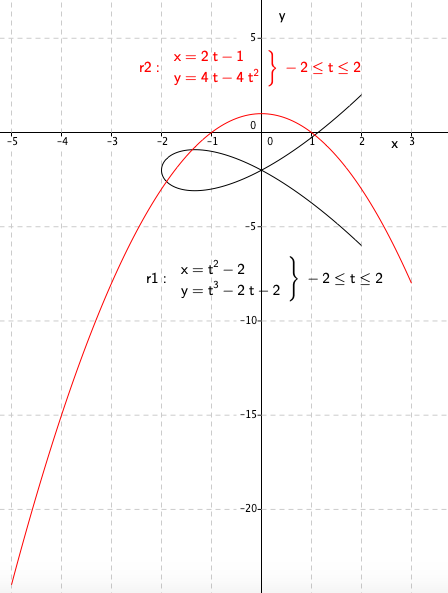
===a)=== | |||
[[File: r1-v2020-2-3a.png ]] | |||
===b)=== | |||
Vi finner fartsvektorene ved å derivere posisjonsvektorene: | |||
$\vec{v_1 (t)} = (\vec{r_1(t)})' = [2t,3t^2-2 ] \\ \vec{v_2 (t)} = (\vec{r_2(t)})' = [2,4-8t ]$ | |||
Banefarten til partikkel 1 blir da: $ | \vec{v_1(-1) }| = \sqrt{4 +1} = \sqrt 5$ | |||
Banefart partikkel 2: $ | \vec{v_2(-1) }| = \sqrt{4 +144} = \sqrt{148} = 2 \sqrt{37}$ | |||
Banefarten er henholdsvis ca. 2,2 m/s og ca. 12,2 m/s når t = - 1. | |||
===c)=== | |||
Dersom begge partiklene skal ha samme fartsrettning må forholdet mellom fartskomponentene i x retning og y- retning være den samme: | |||
[[File: R1-v2020-2-3c.png ]] | |||
Fartsretningen er den samme ved t = - 0,28 sek og ved t = 0,65 sek. | |||
===d)=== | |||
[[File: R1-v2020-2-3d1.png ]] | |||
[[File: R1-v2020-2-3d2.png ]] | |||
==Oppgave 4== | |||
===a)=== | |||
Trekanten ABC er formlik med ADC og med BCD, fordi alle tre har en vinkel på 90 grader, og en annen vinkel felles. Alle vinklene ti trekantene er derved like. | |||
Trekantene AEB, CBF og ACG er speilinger av de før nevnte, altså har de samme form - formlike. Når man speiler endres ikke vinkler i trekantene, eller lengder, man kan tenke seg at man forandrer betraktningspunjtet, altså fra hvor man ser objektet. | |||
===b)=== | |||
Siden de omtalte trekantene er formlike vil forholdet mellom samsvarende sider være konstant, k. | |||
===c)=== | |||
Dersom vi bretter inn "flikene" F, G og E i trekanten ABC, ser vi at trekantene BCF og ACG akkurat dekker trekanten ABC, arealene er like store. Det samme gjør trekanten ABE. | |||
Da får man: | |||
$A_{\triangle BCF} + A_{\triangle ACG} = A_{\triangle ABE} \\ $ | |||
Siste sideversjon per 29. mar. 2022 kl. 13:35
Diskusjon av denne oppgaven på matteprat
Løsningsforslag til del 1 av Kristian Saug
Løsningsforslag del 2 av Kristian Saug
Løsningsforslag av Svein Arneson
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsninger til del 1 laget av Lektor Håkon Raustøl
Videoløsninger til del 2 laget av Lektor Håkon Raustøl
Løsningsforslag del 1 video av Lektor Lainz
Løsningsforslag del 2 video av Lektor Lainz
Oppgave 1
a)
$f(x)=x^6 + 3x^5 + ln(x) \\ f'(x)= 6x^5+15x^4 + \frac{1}{x}$
b)
$g(x)=2x^2 \cdot e^{2x-1}\\ g'(x) = 4x \cdot e^{2x-1} + 2x^2 \cdot 2 \cdot e^{2x-1} = (1+x)4x \cdot e^{2x-1}$
c)
$h(x) = \frac{4x-1}{x+2} \\ h'(x) = \frac{4(x+2) - (4x-1)}{(x+2)^2} = \frac{9}{(x+2)^2}$
Oppgave 2
a)
$ln(x^2) + ln(x) = 12 \\ 2 ln(x) + ln(x) = 12 \\ 3 ln(x) = 12 \\ e^{ln(x)} = e^4 \\ x = e^4 $
b)
$e^{2x}-e^x =6 \\(e^x)^2 - e^x - 6 =0 \\ u = e^x \\ u^2-u-6=0 \\ u = 3 \vee u = -2 \\ e^x = 3 \vee e^x = -2 \\ x = ln(3)$
$e^x =-2$ har ingen løsning.
Oppgave 3
$\vec{u} \cdot \vec{v } =-2$ og $|\vec u | = 3$ og $ |\vec v | = 2$
$\vec a = 2 \vec u + 3 \vec v$ og $ \vec b = t \cdot \vec u + 5 \vec v$
a)
Dersom to vektorer er parallelle:
$ k \vec{a} = \vec{b} \\ k(2 \vec u + 3 \vec v) = t \cdot \vec u + 5 \vec v \\ 2k \vec u = t \cdot u \wedge 3k \cdot \vec v = 5 \vec v \\ t = 2k \wedge k = \frac 53 \\ t = \frac{10}{3}$
b)
Når to vektorer står normalt på hverandre er skalarproduktet null:
$ (2 \vec{ u} + 3 \vec {v})(t \cdot \vec u + 5 \vec v )= 0 \\ 2 \cdot t \cdot \vec {u^2} + 10 \cdot \vec{ u} \cdot \vec v + 3 \cdot t \cdot \vec u \cdot \vec v + 15 \vec{ v^2}$
Fra oppgaveteksten vet vi at: $\vec{u^2} = | \vec {u} | \cdot |\vec {u} | =9 \\ \vec{v^2} = | \vec{v} | \cdot | \vec{v} | = 4 \\ \vec{u} \cdot \vec{v} = -2$
Setter inn og får:
$2 \cdot t \cdot 9 +10 \cdot (-2) + 3 \cdot t \cdot(-2) + 15 \cdot 4 =0 \\ 12t = -40 \\ t = - \frac{10}{3}$
Oppgave 4
a)
Dersom polynomet går opp i (x-1) må P(1) være lik null:
$P(1) = 6 \cdot 1^3-5 \cdot 1^2-2 \cdot 1 +1 = 6-5 -2+1=0$, altså går divisjonen P(x) : (x-1) opp.
b)
Faktoriserer så $6x^2+x-1$:
$x= \frac{-1 \pm \sqrt{1-4 \cdot 6 \cdot (-1)}}{12} =\frac{-1 \pm 5}{12} \\ x = - \frac 12 \vee x= \frac 13 $
$6x^2+ x -1 = 6(x + \frac 12)(x - \frac 13) = (2x+1)(3x-1)$
Altså kan man skrive:
$P(x)= (x-1)(2x+1)(3x-1)$
c)
$F(x) = \frac{P(x)}{(x^2-1)} = \frac{(2x+1)(3x-1)}{(x+1)}$
Nå må vi huske at nevneren fører til at F(x) ikke er definert for x = -1 eller for x = 1.
Setter inn i et fortegnsskjema, for å drøfte fortegnet til F(x):
Vi får tre områder der F er større eller lik null:
$x \in < -1, - \frac 12] \cup [ \frac 13 , 1> \cup < 1, \rightarrow>$
d)
$P(x)= (x-1)(2x+1)(3x-1)$ og $F(x)= \frac{P(x)}{x^2-1} = \frac{(x-1)(2x+1)(3x-1)}{(x+1)(x-1)} = \frac{(2x+1)(3x-1)}{(x+1)}$
$\lim\limits_{x \to 1} F(x) = \frac{(2 \cdot 1+1)(3 \cdot 1-1)}{(1+1)} = \frac 62 =3$
$\lim\limits_{x \to -1} F(x) = \frac{(2 \cdot -1+1)(3 \cdot -1-1)}{(-1+1)} = $
Når x går mot -1 går telleren mot 4 og nevneren mot 0. Grensen eksisterer ikke.
Oppgave 5
a)
Vi velger 3 av 8 bøker. Rekkefølgen vi trekker i har ikke betydning. Hvor mange kombinasjoner finnes? :
$3C8 = \frac{8!}{5! \cdot 3!} = \frac {8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} = 8 \cdot 7 = 56$
Det er mulig å velge 56 kombinasjoner av bøker.
b)
Dette er en hypergeometrisk situasjon. Vi trekker 4 og 3 skal være riktige:
$\frac{\binom{3}{3} \binom{5}{1}}{ \binom{8}{4}} = \frac{1 \cdot 5 }{70} = \frac {1}{14} $
c)
Det "motsatte" av minst to er null og en; dersom drikke får minst to, får du enten null eller en.
Vi finner P (minst to bøker) = 1 - ( P( null bøker) + P( en bok) )
På matematikkspråk er dette sannsynligheten av komplementære hendelser, og ikke "motsatte" som vi skrev over.
$P(x=0) = \frac{\binom{3}{0} \binom{5}{4}}{ \binom{8}{4}} = \frac{1 \cdot 5 }{70} = \frac {1}{14} $
$P(x=1) = \frac{\binom{3}{1} \binom{5}{3}}{ \binom{8}{4}} = \frac{1 \cdot 5 }{70} = \frac {3}{7} $
Vi får da P( minst to riktige bøker) = $1- \frac {1}{14} - \frac 37 = 0,5$ , altså 50 % sjanse for minst to riktige.
Vi kunne også ha regnet ut sannsynligheten for to riktige og lagt det til sannsynligheten for tre, som vi regnet ut i b, kanskje litt tidsbesparende.
Oppgave 6
a)
AB har lengden 6 og DC har lengden 2x. Høyden er f(x):
$F(x) = \frac{6+2x}{2} \cdot (9-x^2) = -x^3 - 3x^2 +9x+ 27$
b)
$F'(x) = -3x^2-6x+9$
$F'(x) = 0 $ gir x= -3 eller x = 1.
Av uttrykket for den deriverte ser man at den deriverte går fra positv til negativ i nullpunktet x = 1 ( parabelen vender sin hule side ned.)
$F(1)= -1-3 + 9 + 27 = 32$
Størst areal er 32, når x = 1.
Oppgave 7
Vinkel D er 65 grader, da er vinkel w = 130 grader. (periferi / sentral vinkel) Av samme grunn er u = 65 grader. I trekanten BCE er vinkelen i E (180-35-65) grader = 80 grader. Det gjør at vinkel v = 100 grader.
Oppgave 8
a)
Linjen l har parameterfremstilling:
$ l: \left\{ \begin{array}{rcl} x=t \\ y=2t+1 \end{array}\right. $
For en vilkårlig t verdi er D (t, 2t + 1)
$\vec{AD} = [ t - (-1), (2t+1) - 1 ] = [ t+1 , 2t]$, som skulle vises.
b)
$\vec{AD} = [t+1, 2t ]$ og $\vec {CD} = [t-7, 2t - 4]$
Lengden av AD og CD vektor skal være like.
$|\vec{AD}|^2 = |\vec{CD}|^2 \\ (t+1)^2+ 4t^2 = (t-7)^2 + (2t-4)^2 \\ t^2+2t+1+4t^2 = t^2-14t+49+4t^2-16t+16 \\32t =64 \\ t=2 $
Som innsatt gir D (2, 5)
Koordinatene til punkt B:
$\vec{OB} = \vec{OA} + \vec{AB} = \vec{OA} - \vec {CD} = [-1, 1] - [-5, 0] = [4, 1]$
Punktet B har koordinatene (4, 1).
DEL TO
Oppgave 1
a)
Situasjonen er i utgangspunktet hypergeometrisk.
For å kunne regne binomisk:
Tellingen av en bil skal ikke påvirke den neste. Dersom hun teller bilene i en "elbil kortesje" blir det feil. Hun må anta at populasjonen av biler er stor i forhold til de 100 hun teller, slik at det ikke endrer sannsynligheten (man kan tenke at å telle en bil er det samme som å trekke ut, uten tilbakelegging. Dersom populasjonen er stor i forhold til utvalget vil ikke sannsynligheten påvirkes i nevneverdig grad.)
b)
c)
Oppgave 2
a)
Begge linjene har stigningstall 5, altså er de parallelle.
b)
Som skulle vises.
Oppgave 3
a)
b)
Vi finner fartsvektorene ved å derivere posisjonsvektorene:
$\vec{v_1 (t)} = (\vec{r_1(t)})' = [2t,3t^2-2 ] \\ \vec{v_2 (t)} = (\vec{r_2(t)})' = [2,4-8t ]$
Banefarten til partikkel 1 blir da: $ | \vec{v_1(-1) }| = \sqrt{4 +1} = \sqrt 5$
Banefart partikkel 2: $ | \vec{v_2(-1) }| = \sqrt{4 +144} = \sqrt{148} = 2 \sqrt{37}$
Banefarten er henholdsvis ca. 2,2 m/s og ca. 12,2 m/s når t = - 1.
c)
Dersom begge partiklene skal ha samme fartsrettning må forholdet mellom fartskomponentene i x retning og y- retning være den samme:
Fartsretningen er den samme ved t = - 0,28 sek og ved t = 0,65 sek.
d)
Oppgave 4
a)
Trekanten ABC er formlik med ADC og med BCD, fordi alle tre har en vinkel på 90 grader, og en annen vinkel felles. Alle vinklene ti trekantene er derved like.
Trekantene AEB, CBF og ACG er speilinger av de før nevnte, altså har de samme form - formlike. Når man speiler endres ikke vinkler i trekantene, eller lengder, man kan tenke seg at man forandrer betraktningspunjtet, altså fra hvor man ser objektet.
b)
Siden de omtalte trekantene er formlike vil forholdet mellom samsvarende sider være konstant, k.
c)
Dersom vi bretter inn "flikene" F, G og E i trekanten ABC, ser vi at trekantene BCF og ACG akkurat dekker trekanten ABC, arealene er like store. Det samme gjør trekanten ABE.
Da får man:
$A_{\triangle BCF} + A_{\triangle ACG} = A_{\triangle ABE} \\ $