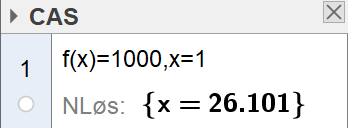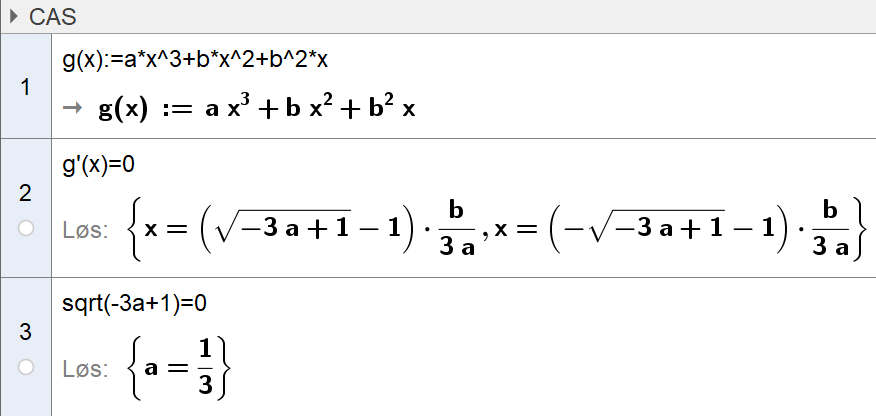S1 2019 høst LØSNING: Forskjell mellom sideversjoner
| (3 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 322: | Linje 322: | ||
===a)=== | ===a)=== | ||
[[File: | [[File: oppg4a1.png]] | ||
===b)=== | ===b)=== | ||
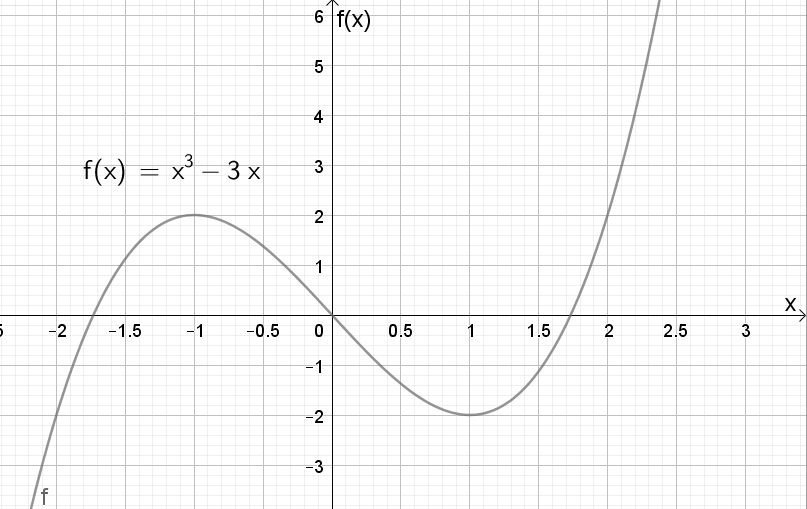
Tangentene til $f$ er parallelle med x-aksen der den deriverte er lik 0, altså i ekstremalpunktene. | |||
[[File: oppg4b.png]] | |||
A=(-1,2) og B=(1,-2) | |||
===c)=== | |||
[[File: oppg4c.png]] | |||
De to tangentene er $y=9x+16$ og $y=9x-16$ | |||
===d)=== | |||
[[File: oppg4d.png]] | |||
Dersom $a=\frac{1}{3}$ er $g'(x)=0$ i bare ett punkt, og grafen til $g$ har derfor bare én tangent som er parallell med x-aksen. | |||
Siste sideversjon per 29. des. 2019 kl. 11:38
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Svein Arneson
Løsningsforslag del 1 laget av Emilga
Løsningsforslag del 2 laget av Kristian Saug
DEL 1
Oppgave 1)
a)
$x^2+4x-12=0 \\ (x-2)(x+6)=0 \\ x=-6 \vee x=2$
b)
$lg(5-2x)=1 \\ 5-2x =10 \\ -2x = 5 \\ x= -\frac{5}{2}$
Oppgave 2)
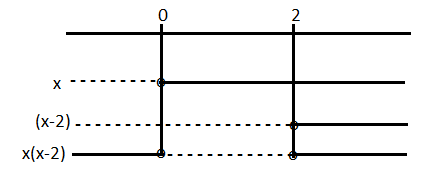
$x^2-2x<0$
Finner nullpunktene.
$x(x-2)=0 \\ x=0 \vee x=2$
$x^2-2x<0$ når $0<x<2$
Oppgave 3)
$x^2+4y=4x \\ 4x-2y=6$
Ganger likning II med 2 og bruker addisjonsmetoden.
Likning II ganger 2:
$8x-4y=12$
Legger sammen likningene:
$x^2+4y+8x-4y=4x+12 \\ x^2+4x-12=0 \\ x_1=-6 \vee x_2=2$
(Samme likning som i oppgave 1a)
Gjør om likning II:
$4x-2y=6 \\ -2y=6-4x \\ y=-3+2x$
Setter inn de to x-verdiene:
$y_1=-3 + 2\cdot (-6) = -15$
$y_2=-3+2\cdot 2=1$
Løsninger:
$x_1=-6, y_1=-15 \\ x_2=2, y_2=1 $
Oppgave 4)
a)
$(a+2)^3-a\cdot(a+2)^2 \\ =(a+2)(a+2)^2-a\cdot(a+2)^2 \\ =(a+2)^2\cdot((a+2)-a) \\ =(a^2+4a+4)\cdot 2 \\ =2a^2+8a+8$
b)
$\frac{x+1}{x+2}-\frac{x+1}{x-1}-\frac{x+5}{x^2+x-2}$
$=\frac{(x+1)(x-1)}{(x+2)(x-1)}-\frac{(x+1)(x+2)}{(x-1)(x+2)}-\frac{x+5}{(x+2)(x-1)}$
$=\frac{x^2-1}{(x+2)(x-1)}-\frac{x^2+3x+2}{(x-1)(x+2)}-\frac{x+5}{(x+2)(x-1)}$
$=\frac{(x^2-1)-(x^2+3x+2)-(x+5)}{(x+2)(x-1)}$
$=\frac{x^2-1-x^2-3x-2-x-5}{(x+2)(x-1)}$
$=\frac{-4x-8}{(x+2)(x-1)}$
$=\frac{-4(x+2)}{(x+2)(x-1)}$
$=\frac{-4}{x-1}=\frac{4}{1-x}$
c)
$2lg(2x^2)+lg\frac{5}{x}-lg(2x^3)$
$2lg2+2lg(x^2)+lg5-lgx-(lg2+lg(x^3))$
$2lg2 + 4lgx + lg5 - lg x -lg 2 - 3lg x$
$lg 2 + lg 5 = lg (2\cdot5) = lg 10 = 1$
Oppgave 5)
a)
$\binom{7}{3} \cdot \binom{5}{2} = \frac{7\cdot6\cdot5}{3\cdot2\cdot1}\cdot\frac{5\cdot4}{2\cdot1}=35\cdot10=350$
Det er mulig å sette sammen 350 komiteer.
b)
P(Anne og Jens)$=\frac{3}{7}\cdot\frac{2}{5}=\frac{6}{35}$
Sannsynligheten for at både Anne og Jens blir med i komiteen er $\frac{6}{35}$
c)
P(Anne eller Jens) = P(Anne men ikke jens) + P(Jens men ikke Anne)
$=\frac{3}{7}\cdot\frac{3}{5}+\frac{4}{7}\cdot\frac{2}{5} \\ =\frac{9}{35}+\frac{8}{35}=\frac{17}{35}$
Sannsynligheten for at én av dem blir med i komiteen er $\frac{17}{35}$
Oppgave 6)
Kantene i Pascals trekant er alltid 1-ere. Ellers er et tall i Pascals trekant summen av de to tallene over. Utregning av de to midterste tallene som mangler:
$66-11=55$
$495-330=165$
Oppgave 7)
Opplysningene gir oss følgende likningssett, hvor x er prisen for skolegang for ett barn i én måned, og y er prisen for barnehjemsplass for ett barn i én måned.
<math> \left[ \begin{align*} 2x+y=700 \\ 4x+3y=1700 \end{align*}\right] </math>
Uttrykker likning I ved y:
$y=700-2x$
Setter inn verdien av y i likning II:
$4x+3(700-2x)=1700 \\ 4x+2100-6x=1700 \\ -2x = -400 \\ x=200$
Fra likning I:
$y=700-2\cdot 200=700-400=300$
Per barn per måned koster det 200kr for skolegang og 300kr for barnehjemsplass. For 20 barn blir det totalt:
$20\cdot 200kr + 20\cdot 300kr=4000kr+6000kr=10000kr$
Klassen til Kari må samle inn 10 000 kr hver måned.
Oppgave 8)
a)
$K(x)=0,2x^2+50x+2000 \\ K'(x)=0,4x+50 \\ K'(100)=0,4\cdot100+50=40+50=90$
$K'(100)=90$ og dette forteller oss at kostnaden av å øke produksjonen fra 100 til 101 enheter er 90 kr.
b)
$O(x)=-0,3x^2+90x-2000 \\ O'(x)=-0,6x+90$
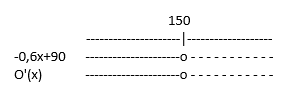
Finner ekstremalpunktet for O(x):
$O'(x)=0 \\ -0,6x+90=0 \\ -0,6x=-90 \\ x=\frac{90}{0,6} \\ x=\frac{900}{6} \\ x=150$
Vi ser at O(x) har et toppunkt i x=150. Den produksjonsmengden som gir størst overskudd er 150 enheter.
c)
$O(x)=I(x)-K(x) \\ I(x)=O(x)+K(x)$
$I(x)=(-0,3x^2+90x-2000)+(0,2x^2+50x+2000) \\ I(x) = -0,3x^2+0,2x^2+90x+50x-2000+2000 \\ I(x)=-0,1x^2+140x$
$I(100)=-0,1\cdot 100^2+140\cdot100=-0,1\cdot10000 + 14000=-1000+14000=13000$
Inntekten ved produksjon og salg av 100 enheter per dag er 13 000 kr.
d)
$O(x)=I(x)-K(x)$
$O(x)=-0,1x^2+a\cdot x - (0,2x^2+50x+2000) \\ O(x)=-0,1x^2-0,2x^2+a\cdot x-50x-2000 \\ O(x)=-0,3x^2+(a-50)x-2000$
$O'(x)=-0,6x+a-50$
Overskuddet er størst når bedriften produserer og selger 100 enheter per dag, altså har vi:
$O'(100)=0$
$-0,6\cdot 100+a-50=0 \\ -60+a-50=0 \\ a=110$
Verdien til a er 110.
Oppgave 9
a)
La x være antall pakker av type A, og y være antall pakker av type B.
Klassen bruker 3 esker fargestifter per Pakke A, og 2 esker fargestifter per Pakke B. Klassen har maksimalt 70 esker fargestifter.
$3x+2y \leq 70 \\ 2y \leq 70-3x \\ y \leq -1,5x+35$
Klassen bruker 2 sprettballer per Pakke A, og 4 sprettballer per Pakke B. Klassen har maksimalt 72 sprettballer.
$2x+4y \leq 72 \\ 4y \leq 72-2x \\ y \leq -0,5x+18 $
Klassen bruker 2 hoppestrikker per Pakke A, og 3 hoppestrikker per Pakke B. Klassen har maksimalt 60 hoppestrikker
$2x+3y \leq 60 \\ 3y \leq 60-2x \\ y \leq -\frac{2x}{3}+20$
I tillegg har vi $x \geq 0$ og $y \geq 0$ fordi klassen må lage 0 eller flere gavepakker (kan ikke lage et negativt antall gavepakker).
Dersom vi tegner disse fem ulikhetene i samme koordinatsystem, vil det skraverte området oppfylle alle ulikhetene samtidig.
b)
Vi sjekker de fire hjørnene i det skraverte området for å se hvilken fordeling av x og y som gir maksimalt antall gavepakker, x+y.
Hjørnet i (0,18) gir $0+18=18$ pakker totalt.
Hjørnet i (12,12) gir $12+12=24$ pakker totalt.
Hjørnet i (18,8) gir $18+8=26$ pakker totalt.
Hjørnet i ca. (23.5 ,0) gir $23+0=23.5$ pakker totalt.
Det maksimale antall gavepakker klassen kan lage er 18 pakker av type A og 8 pakker av type B, til sammen 26 pakker totalt.
DEL 2
Oppgave 1)
a)
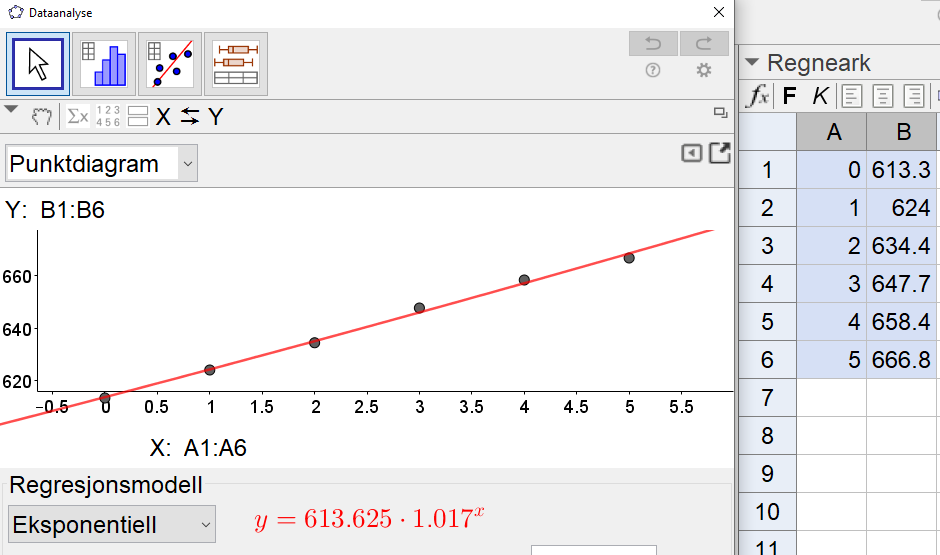
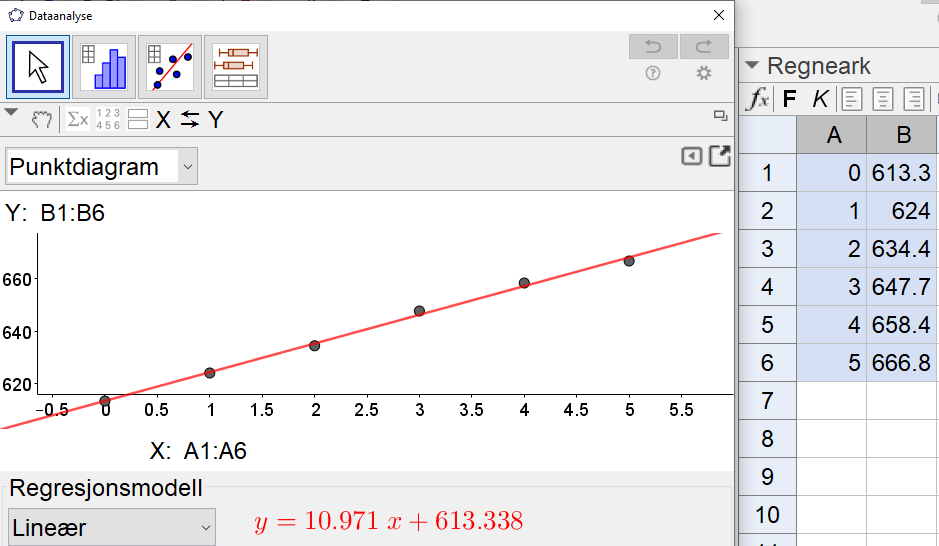
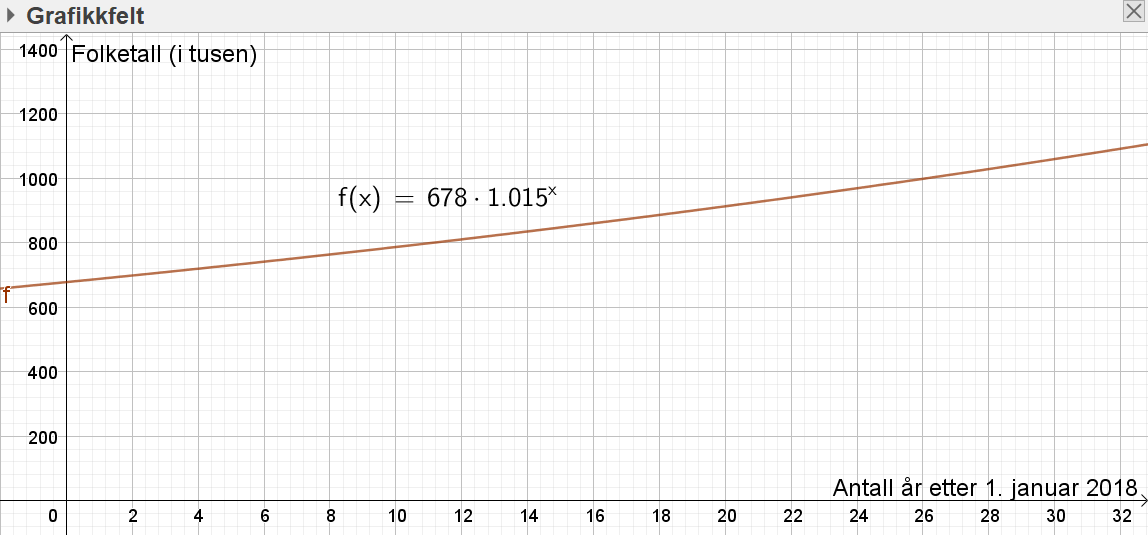
Utfører regresjonsanalyse i Geogebra.
En eksponentiell modell brukes ofte for befolkningsvekst, og gir $g(x)=613.6\cdot 1.017^x$. Vi kan se i statistikken (trykk på $\Sigma x$ i Geogebra) at modellen passer godt fordi $R^2=0.9962$.
En lineær modell passer likevel enda bedre til dataene i dette tilfelle ($R^2=0.997$), og gir $g(x)=10.97x+613.34$.
b)
c)
Bruker CAS i Geogebra. Husk at folketallet i modellen $f$ er oppgitt i tusener.
Ifølge modellen $f$ vil folketallet passere 1 million etter 26,1 år. Denne oppgaven kan også løses grafisk.
d)
Definerer modellen $h(x)$ for befolkningsveksten i Stockholm (linje 2 i CAS).
$p$ må være 0,398 dersom Oslo skal ha samme folketall som Stockholm i januar 2050. Det vil si at Stockholm må ha en vekst i folketallet på 0,398% per år.
Oppgave 2)
La x være antall elbiler i 2018 og y være antall bensinbiler i 2018.
Forhandleren solgte 28 elbiler og 34 bensinbiler i 2018.
Oppgave 3)
Bruker sannsynlighetskalkulatoren i Geogebra i hele oppgaven.
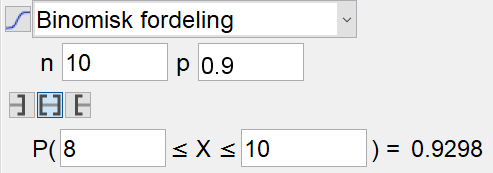
a)
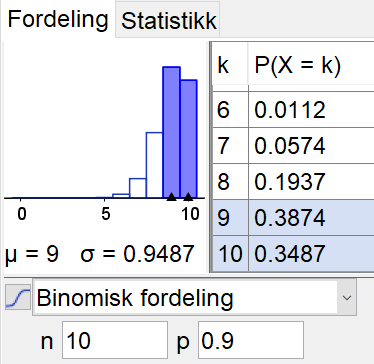
Sannsynligheten for at Jonas treffer blink på minst 8 av de 10 skuddene fra liggende stilling er ca. 93%.
b)
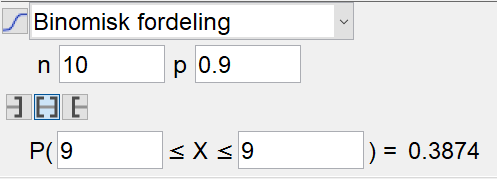
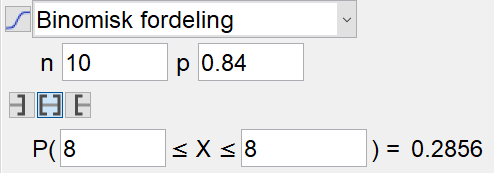
Sannsynligheten for at Jonas treffer blink på nøyaktig 9 skudd fra liggende stilling:
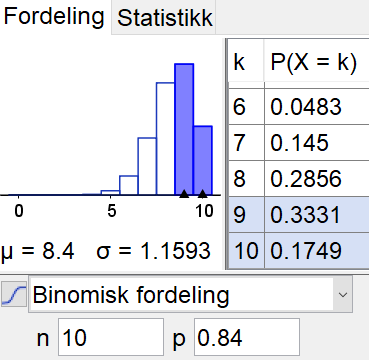
Sannsynligheten for at Jonas treffer blink på nøyaktig 8 skudd fra stående stilling:
P(9 treff liggende og 8 treff stående)$=0.3874\cdot0.2856=0.11$
Sannsynligheten for at Jonas treffer blink på nøyaktig 9 skudd fra liggende stilling og nøyaktig 8 skudd fra stående stilling er 11%.
c)
For at Jonas skal treffe blink på minst 19 av 20 skudd, må han treffe enten 9 liggende og 10 stående, 10 liggende og 9 stående, eller 10 liggende og 10 stående. Finner sannsynligheten for hver hendelse i sannsynlighetskalkulatoren i Geogebra.
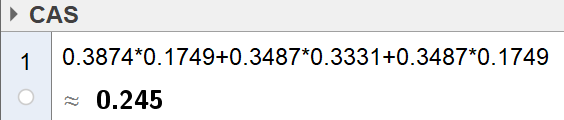
Bruker CAS for å regne ut P(minst 19 av 20 treff) = P(9 treff liggende)*P(10 treff stående) + P(10 treff liggende)*P(9 treff stående) + P(10 treff liggende)*P(10 treff stående)
Sannsynligheten for at Jonas treffer blink på minst 19 av 20 skudd er 24,5%.
Oppgave 4)
a)
b)
Tangentene til $f$ er parallelle med x-aksen der den deriverte er lik 0, altså i ekstremalpunktene.
A=(-1,2) og B=(1,-2)
c)
De to tangentene er $y=9x+16$ og $y=9x-16$
d)
Dersom $a=\frac{1}{3}$ er $g'(x)=0$ i bare ett punkt, og grafen til $g$ har derfor bare én tangent som er parallell med x-aksen.