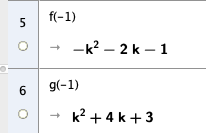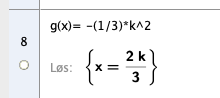1T 2019 høst LØSNING: Forskjell mellom sideversjoner
| (43 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 36: | Linje 36: | ||
Uttrykket i ulikheten er ferdig faktorisert, så man kan sette opp et fortegnsskjema med en gang og finne ut når uttrykket på venstre side er større enn null. | Uttrykket i ulikheten er ferdig faktorisert, så man kan sette opp et fortegnsskjema med en gang og finne ut når uttrykket på venstre side er større enn null. | ||
[[File:1t-h19-1-3b.png]] | |||
$x \in < -2,4>$ | |||
===Oppgave 4=== | ===Oppgave 4=== | ||
| Linje 52: | Linje 58: | ||
$ lg( \frac{\sqrt{50}}{x}) = \frac 12 \\ 10^{lg (\frac{\sqrt{50}}{x})} = 10 ^{\frac 12} \\ \sqrt{50} = x \sqrt{10} \\ x = \frac{\sqrt{50}}{\sqrt{10}} = \sqrt{\frac{50}{10}}\\ x = \sqrt 5$ | $ lg( \frac{\sqrt{50}}{x}) = \frac 12 \\ 10^{lg (\frac{\sqrt{50}}{x})} = 10 ^{\frac 12} \\ \sqrt{50} = x \sqrt{10} \\ x = \frac{\sqrt{50}}{\sqrt{10}} = \sqrt{\frac{50}{10}}\\ x = \sqrt 5$ | ||
===c)=== | |||
$ 2^{x^2} \cdot 2^{3x} =16 \\ 2^{x^2+3x} = 2^4 \\ x^2+3x-4 =0 \\ x= -4 \vee x =1$ | |||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 120: | Linje 131: | ||
===Oppgave 10=== | ===Oppgave 10=== | ||
[[File:1t-h19-2-4.png]] | |||
x= -3: Funksjonen har et toppunkt, men har negativ verdi. | |||
x= 2: Funksjonsverdi fortsatt negativ og funksjonen har et bunnpunkt. | |||
x= 4: Funksjonen vokser (deriverte positiv). Den har et nullpunkt | |||
x= 7: Funksjonen har et terrassepunkt. Den deriverte har et nullpunkt, men samme fortegn (positiv) på begge sider av nullpunktet. | |||
===Oppgave 11=== | ===Oppgave 11=== | ||
| Linje 148: | Linje 170: | ||
===a)=== | ===a)=== | ||
I området 0 - 180 grader har en sinusverdi to løsninger. | I området 0 - 180 grader har en sinusverdi to løsninger (sjekk enhetssirkelen). | ||
Vi har symmetri, så dersom en vinkel er $53,5^{\circ}$ så er den andre $180^{\circ} - 53,5^{\circ}$ | Vi har symmetri, så dersom en vinkel er $53,5^{\circ}$ så er den andre $180^{\circ} - 53,5^{\circ} =126,5^{\circ}$ | ||
===b)=== | ===b)=== | ||
[[File:1t-h19-1-13-b.png]] | |||
==DEL TO== | ==DEL TO== | ||
| Linje 185: | Linje 208: | ||
|Sum | |Sum | ||
|- | |- | ||
| | |1T | ||
| $ 6$ | | $ 6$ | ||
| $ 8$ | | $ 8$ | ||
| 14 | | 14 | ||
|- | |- | ||
|ikke | |ikke 1T | ||
|$6$ | |$6$ | ||
|$10$ | |$10$ | ||
| Linje 203: | Linje 226: | ||
===b)=== | ===b)=== | ||
P (tysk, men ikke | P (tysk, men ikke 1T) = $\frac {6}{30} = \frac 15$ | ||
===c)=== | ===c)=== | ||
P( tysk, gitt ikke | P( tysk, gitt ikke 1T) = $\frac{6}{16} = \frac 38$ | ||
==Oppgave 3== | ==Oppgave 3== | ||
Regner i CAS: | |||
[[File:1t-h19-2-3.png]] | |||
Finner BC ved pytagoras, har formlikhet i de to trekanten og finner så DE = 4. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
[[File:1t-h19-2-4-a.png]] | |||
Bruker pytagoras og får at $ CD = \sqrt{3}a $ | |||
===b)=== | |||
Vinkel ACD er 30 grader fordi trekanten er rettvinklet og hypotenusen er dobbelt så lang som korteste katet. Vinkel BCA blir da 135 grader. | |||
Bruker cosinussetningen og får | |||
[[File:1t-h19-2-4-bversjon2.png]] | |||
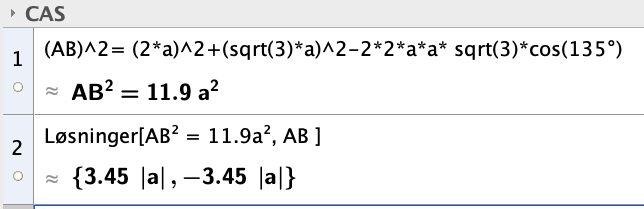
Det positive utrykket er svaret, $AB = 3,45 \cdot a$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
[[File:1t-h19-2-5-a.png]] | |||
Nullpunkter: x = 0 eller x = k ( linje 3) | |||
===b)=== | |||
Linje 4 i a: | |||
$f'(x) =3x^2 - 4kx + k^2$ | |||
===c)=== | |||
Både figur A og C stemmer med nullpunkter og ekstremalpunktets x verdi. Vi sjekker funksjonen og den deriverte for x = -1: | |||
[[File:1t-h19-2-5-c.png]] | |||
Vi ser at funksjonsverdien er negativ og den deriverte positiv, altså er det figur C som viser grafen til f. | |||
===d)=== | |||
Bruker linje (punkt)(punkt) kommando i CAS og får: | |||
[[File:1t-h19-2-5-d.png]] | |||
Stigningstall: $- \frac{2k^2}{9}$ | |||
===e)=== | |||
[[File:1t-h19-2-5-e.png]] | |||
Setter den deriverte lik $- \frac{k^2}{3}$ og får bare ett svar som tilfredsstiller likningen, | |||
$ x= \frac{2k}{3} $. | |||
Finner y koordinaten til punktet ved å sette resultatet over inn i f: | |||
[[File:1t-h19-2-5-e2.png]] | |||
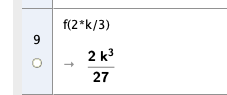
Tangeringspunkt : $ ( \frac{2k}{3},\frac{2k^3}{27} )$ | |||
Siste sideversjon per 10. feb. 2020 kl. 20:44
Diskusjon av denne oppgaven på matteprat
Løsningsforslag del 1 laget av mattepratbruker Emilga
Løsningsforslag del 2 laget av mattepratbruker Kristian Saug
DEL EN
Oppgave 1
$\frac{0,00046 \cdot 25000000}{0,05} = \frac{4,6 \cdot 10^{-4} \cdot 25 \cdot 10^6}{5 \cdot 10^{-2}} = 4,6 \cdot 5 \cdot 10^{-4+6+2} = 23 \cdot 10^{4} = 2,3 \cdot 10^{5}$
Oppgave 2
<math> \left[ \begin{align*} 2x + 3y =6 \\ 5x + 6y =18 \end{align*}\right] </math>
Velger å bruke addisjonsmetoden. Multipliserer første likning med -2:
<math> \left[ \begin{align*} -4x - 6y = -12 \\ 5x + 6y =18 \end{align*}\right] </math>
Legger likningene sammen og får:
x = 6
Setter x = 6 inn i første likning og får y = - 2
Løsning: ( 6, -2)
Oppgave 3
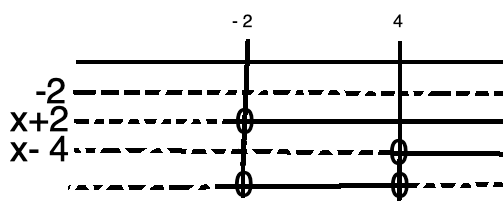
-2 (x+2)( x - 4) > 0
Uttrykket i ulikheten er ferdig faktorisert, så man kan sette opp et fortegnsskjema med en gang og finne ut når uttrykket på venstre side er større enn null.
$x \in < -2,4>$
Oppgave 4
$ \frac{2x^2+x+3}{x^2-9} - \frac{x}{x+3} = \frac{2x^2+x+3-x(x-3)}{(x+3)(x-3)} = \frac{x^2+4x+3}{(x+3)(x-3)} = \frac{(x+3)(x+1)}{(x+3)(x-3)} = \frac{x+1}{x-3}$
Oppgave 5
a)
$lg(4x)= 0 \\ 10^{lg(4x)} = 10^0 \\ 4x=1 \\ x = \frac 14$
b)
$ lg( \frac{\sqrt{50}}{x}) = \frac 12 \\ 10^{lg (\frac{\sqrt{50}}{x})} = 10 ^{\frac 12} \\ \sqrt{50} = x \sqrt{10} \\ x = \frac{\sqrt{50}}{\sqrt{10}} = \sqrt{\frac{50}{10}}\\ x = \sqrt 5$
c)
$ 2^{x^2} \cdot 2^{3x} =16 \\ 2^{x^2+3x} = 2^4 \\ x^2+3x-4 =0 \\ x= -4 \vee x =1$
Oppgave 6
Den rette linjen som går gjennom ( -7, -1) og (5, 2):
En rett linje kan skrives som y = ax + b
Finner stigningstallet a:
$a = \frac{\Delta y}{\Delta x}= \frac{2-(-1)}{5-(-7)} = \frac{2+1}{5+7} = \frac 14$
Du kan nå bruke ettpunktsformelen, eller tenke:
$y = ax+b \\ 2= \frac 14 \cdot 5+b \\ b= \frac 34 $
Likningen for linjen er da:
$y = \frac 14 x + \frac 34$
Oppgave 7
$ax^2+3x+1=x-2 \quad x \neq 0 \\ ax^2+2x+3 =0$
Fra abc- formelen vet vi at en løsning oppstår dersom $b^2 - 4ac= 0$ :
$2^2-4 \cdot a \cdot3 = 0 \\4 - 12a =0 \\ a = \frac 13$
a lik en tredjedel gir en løsning.
Oppgave 8
a)
$f(x)= x^3+4x^2+x-6 \\ f'(x) = 3x^2 + 8x+1$
b)
Momentan vekstfart i (-3, f(-3)):
$f'(-3)= 3 \cdot (-3)^2 + 8 \cdot (- 3) + 1 = 27 -24 + 1 = 4$
c)
Gjennomsnittlig vekstfart [ -1, 2 ]:
$f(-1)= (-1)^3+4(-1)^2+(-1)-6 = -1+4-1-6= - 4 \\ f(2) = 2^3+4\cdot 2^2+2-6 = 8+16 + 2 -6 = 20 \\ \frac{f(2)-f(-1)}{3} = \frac{20 - (-4)}{3} = 8$
Den gjennomsnittlige vekstfarten i intervallet er 8.
Oppgave 9
a)
b)
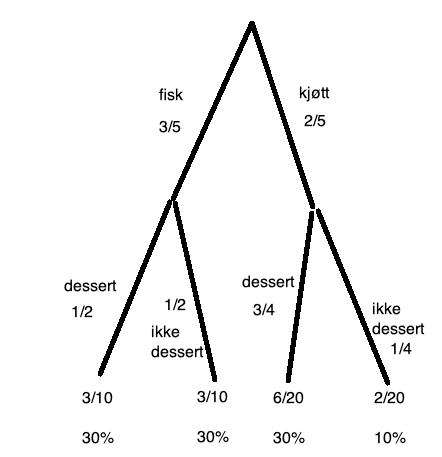
Fra valgtre:
$P(des) = \frac35 \cdot \frac 12 + \frac 25 \cdot \frac 34 = \frac {3}{10} + \frac {6}{20} = \frac{6}{10}$
60% ønsket dessert.
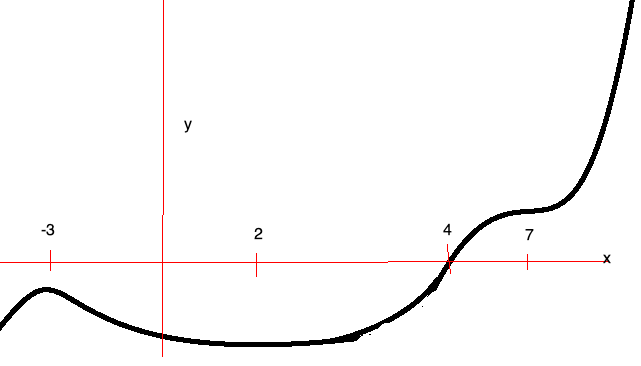
Oppgave 10
x= -3: Funksjonen har et toppunkt, men har negativ verdi.
x= 2: Funksjonsverdi fortsatt negativ og funksjonen har et bunnpunkt.
x= 4: Funksjonen vokser (deriverte positiv). Den har et nullpunkt
x= 7: Funksjonen har et terrassepunkt. Den deriverte har et nullpunkt, men samme fortegn (positiv) på begge sider av nullpunktet.
Oppgave 11
a)
Bruker pytagoras:
$x^2 + x^2 = (4 \sqrt2)^2 \\ 2x^2 = 32 \\ x^2 = 14 \\ x =4 $
b)
$ \tan(v) = \frac{motstående kat}{hosliggende kat} = \frac 44 = 1$
c)
$ \sin(v) = \frac{motståendekatet}{hypotenus} = \frac{4}{4 \sqrt {2}} = \frac{1}{\sqrt {2}} = \frac{\sqrt {2}}{\sqrt {2} \cdot \sqrt {2}} = \frac {\sqrt {2}}{2} $
Oppgave 12
Vi bruker arealsetningen:
$A = abSinC = 3\sqrt2 \cdot 8 \cdot \frac{\sqrt 2}{2} = 3 \cdot 2 \cdot 4 = 24$
Nå var sinus til vinkelen oppgitt i forrige oppgave. Dersom du ikke husker den kan du utlede den ved å tegne en rettvinklet trekant med hypotenus 1.
Oppgave 13
a)
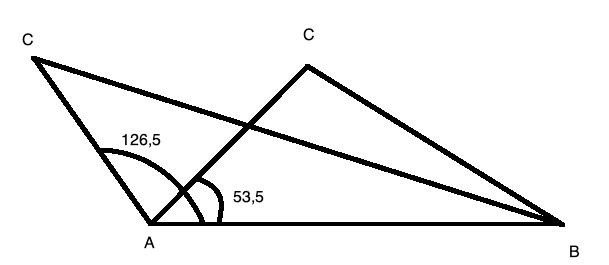
I området 0 - 180 grader har en sinusverdi to løsninger (sjekk enhetssirkelen).
Vi har symmetri, så dersom en vinkel er $53,5^{\circ}$ så er den andre $180^{\circ} - 53,5^{\circ} =126,5^{\circ}$
b)
DEL TO
Oppgave 1
a)
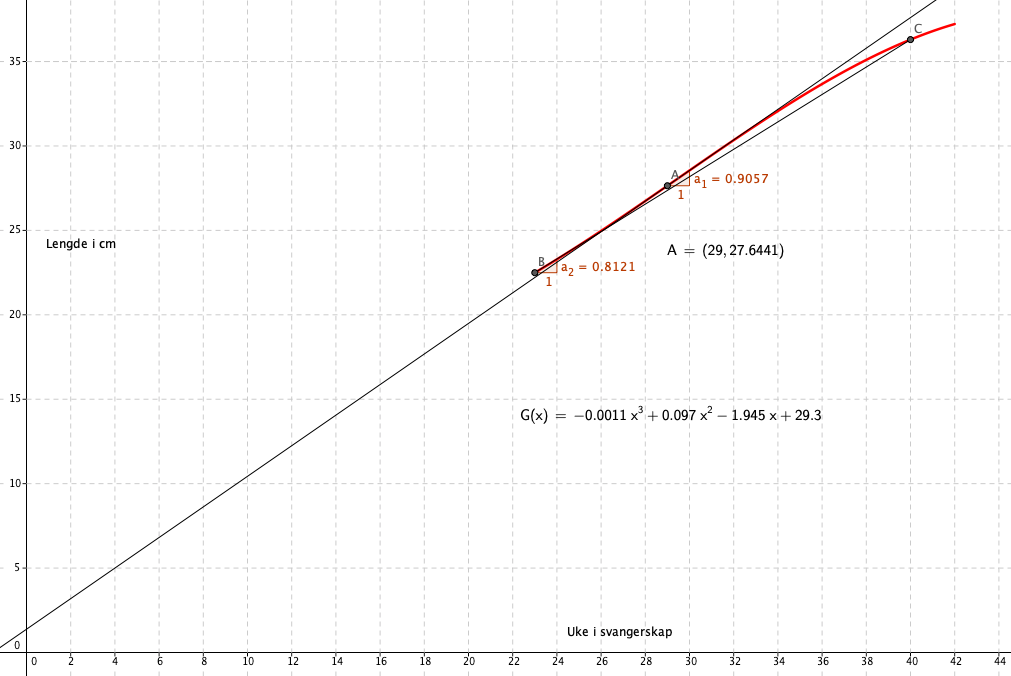
b)
I uke 29 er den momentane vekstfarten 0,9 cm. Det betyr at avstanden øker 0,9 cm i uke 29.
c)
Økningen i denne perioden er i gjennomsnitt ca 8 mm per uke. Se figur i a.
Oppgave 2
a)
| Tysk | ikke Tysk | Sum | |
| 1T | $ 6$ | $ 8$ | 14 |
| ikke 1T | $6$ | $10$ | 16 |
| Sum | 12 | 18 | 30 |
b)
P (tysk, men ikke 1T) = $\frac {6}{30} = \frac 15$
c)
P( tysk, gitt ikke 1T) = $\frac{6}{16} = \frac 38$
Oppgave 3
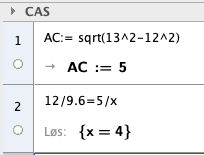
Regner i CAS:
Finner BC ved pytagoras, har formlikhet i de to trekanten og finner så DE = 4.
Oppgave 4
a)
Bruker pytagoras og får at $ CD = \sqrt{3}a $
b)
Vinkel ACD er 30 grader fordi trekanten er rettvinklet og hypotenusen er dobbelt så lang som korteste katet. Vinkel BCA blir da 135 grader.
Bruker cosinussetningen og får
Det positive utrykket er svaret, $AB = 3,45 \cdot a$
Oppgave 5
a)
Nullpunkter: x = 0 eller x = k ( linje 3)
b)
Linje 4 i a:
$f'(x) =3x^2 - 4kx + k^2$
c)
Både figur A og C stemmer med nullpunkter og ekstremalpunktets x verdi. Vi sjekker funksjonen og den deriverte for x = -1:
Vi ser at funksjonsverdien er negativ og den deriverte positiv, altså er det figur C som viser grafen til f.
d)
Bruker linje (punkt)(punkt) kommando i CAS og får:
Stigningstall: $- \frac{2k^2}{9}$
e)
Setter den deriverte lik $- \frac{k^2}{3}$ og får bare ett svar som tilfredsstiller likningen,
$ x= \frac{2k}{3} $.
Finner y koordinaten til punktet ved å sette resultatet over inn i f:
Tangeringspunkt : $ ( \frac{2k}{3},\frac{2k^3}{27} )$