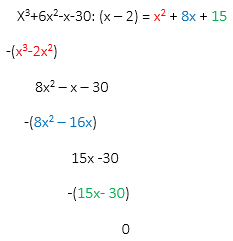R1 2019 høst LØSNING: Forskjell mellom sideversjoner
m de resterende sidene trenger ikke være parallelle, så det blir et trapes |
|||
| (108 mellomliggende versjoner av 5 brukere er ikke vist) | |||
| Linje 3: | Linje 3: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=50110 Diskusjon av oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=50110 Diskusjon av oppgaven på matteprat] | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=50110&start=45#p233038 Løsningsforslag del 2 fra Kristian Saug] | |||
[https://drive.google.com/open?id=14IWzyzURUg1beFWSqELyhiAx2E4WHRes Løsningsforslag (pdf)] fra joes | |||
[https://matematikk.net/matteprat/download/file.php?id=2706 Løsningsforslag fra Svein Arneson] | |||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHXFLfGePzut_A4UVp8gpe3o Løsning del 1 som video av Lektor Håkon Raustøl] | |||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHUVr6YMBuzX14CfQvFlf8DM Løsning del 2 som video av Lektor Håkon Raustøl] | |||
[https://matematikk.net/matteprat/download/file.php?id=3359 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | |||
==DEL EN== | ==DEL EN== | ||
| Linje 9: | Linje 20: | ||
===a)=== | ===a)=== | ||
$ f(x)=x^4-2x+ln(x) \\ f'(x)= 4x^3-2+ \frac 1x$ | $$ f(x)=x^4-2x+ln(x) \\ f'(x)= 4x^3-2+ \frac 1x$$ | ||
===b)=== | ===b)=== | ||
| Linje 24: | Linje 35: | ||
===Oppgave 3=== | ===Oppgave 3=== | ||
===a)=== | |||
Dersom P(x) skal deles på (x-2) og gå opp. må P(x) = 0, dvs. P(2) = 0 | |||
$P(2) = 0 \\ 2^3+ 6 \cdot 2^2 + k\cdot 2 -30 =0 \\ 8+24+2k-30=0 \\ k=-1$ | |||
===b)=== | |||
[[File: R1_H19_del1_3b.png]] | |||
Bruker så ABC formel på svaret og får: | |||
$ x^2 + 8x + 15 = 0 \\ x = \frac{-8 \pm \sqrt{64-4 \cdot 1 \cdot 15}}{2} \\ x = \frac{-8 \pm 2}{2} \\ x = -5 \vee x =-3$ | |||
Faktorisert form: | |||
$x^3 +6x^2 - x -30 = (x-2)(x+3)(x+5)$ | |||
===c)=== | |||
Fra b har vi at: | |||
$(x-2)(x+3)(x+5) \leq 0$ | |||
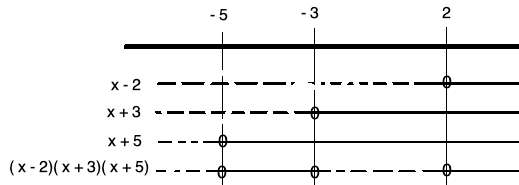
Tegner fortegnsskjema: | |||
[[File: R1_H19_del1_3c.png]] | |||
$x \in < \leftarrow, -5] \cup [-3,2]$ | |||
==Oppgave 4== | |||
===Oppgave 6=== | ===a)=== | ||
$\vec{AB} = [(2-(-2), -1-1] = [4,-2] \\ \vec{BC} = [(4-2, 2-(-1)]= [2, 3]$ | |||
===b)=== | |||
$\vec{AB} \cdot \vec{BC} = [4,-2]\cdot[2,3] = 4 \cdot 2 + (-2) \cdot 3 = 8-6 =2 \neq 0$ | |||
To vektorer som er normale på hverandre har skalarprodukt lik null. Disse står ikke 90 grader på hverandre. | |||
===c)=== | |||
$\vec{AD} = [t+2, 2]$ | |||
Bruker skalarprodukt igjen: | |||
$ \vec{AB} \cdot \vec{AD} = 0 \\ [4,-2] \cdot [t +2,2] =0 \\ 4t + 8 - 4 =0 \\ t = -1$ | |||
===d)=== | |||
Et trapes er en firkant der to sider er parallelle. Det kan her skje på to måter: | |||
$\vec{AB} \parallel\vec{CD}$ | |||
eller | |||
$\vec{BC} \parallel\vec{DA}$ | |||
Vi sjekker begge mulighetene. | |||
$\vec{AB} \parallel\vec{CD} \\ \vec{AB} = k \vec{CD} \\ [4,-2] = k [t-4, 1] \\ 4 = kt-4k \wedge -2 = k \\ t =2$ | |||
t = 2 gir ett trapes. | |||
$\vec{BC} \parallel\vec{DA} \\ \vec{BC} = k \vec{DA} \\ [2, 3] = k [-2-t,-2] \\ 2=-2k-kt \wedge 3=-2k \\ k = - \frac 32 \wedge 2 =3 + \frac 32 t \\ t= - \frac 23$ | |||
$t = - \frac 23$ gir også et trapes. | |||
==Oppgave 5== | |||
===a)=== | |||
$\binom{7}{3} \cdot \binom{5}{2} = \frac{7\cdot6\cdot5}{3\cdot2\cdot1}\cdot\frac{5\cdot4}{2\cdot1}=35\cdot10=350$ | |||
Det er mulig å sette sammen 350 komiteer. | |||
===b)=== | |||
P(Anne og Jens)$=\frac{3}{7}\cdot\frac{2}{5}=\frac{6}{35}$ | |||
Sannsynligheten for at både Anne og Jens blir med i komiteen er $\frac{6}{35}$ | |||
===c)=== | |||
P(Anne eller Jens) = P(Anne men ikke jens) + P(Jens men ikke Anne) | |||
$=\frac{3}{7}\cdot\frac{3}{5}+\frac{4}{7}\cdot\frac{2}{5} \\ =\frac{9}{35}+\frac{8}{35}=\frac{17}{35}$ | |||
Sannsynligheten for at én av dem blir med i komiteen er $\frac{17}{35}$ | |||
==Oppgave 6== | |||
===a)=== | |||
Diagonal i rektangelet er alltid 2. Arealet er alltid $ A = x \cdot \sqrt{4-x^2} $. Brukte pytagoras for å finne lengden av OC. | |||
Areal av skravert område blir da | |||
$A_{skravert} = \frac 14 \pi \cdot2^2 - x \cdot \sqrt{4-x^2} = \pi - x \sqrt{4-x^2}$ | |||
===b)=== | |||
Deriverer F(x) og finner maksimumspunktet: | |||
$F'(x) = \\ ( \pi - x \sqrt{4-x^2})' = \\ -(1 \cdot \sqrt{4-x^2} + x \cdot (-2x) \frac 12 (4-x^2)^{- \frac 12}) = \\ -( \sqrt{4-x^2} - \frac{x^2}{ \sqrt{4-x^2}} ) = \\ - ( \frac{(\sqrt{4-x^2})(\sqrt{4-x^2})}{(\sqrt{4-x^2})} -\frac{x^2}{ \sqrt{4-x^2}} ) = \\ - \frac{4-2x^2}{\sqrt{4-x^2}} = \\ \frac{2(x-\sqrt{2}(x+\sqrt{2})}{\sqrt{4-x^2}}$ | |||
Av uttrykket ser vi at $x= \sqrt 2$ gir den deriverte lik null. Dette stemmer også med hva vi vet om største areal av en rektangulær firkant med gitt omkrets, den hvite firkanten vil være et kvadrat. | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
| Linje 46: | Linje 168: | ||
===c)=== | ===c)=== | ||
Trekanten ABC har areal: $A= \frac {a \cdot b}{2}$ | |||
Fra figuren ser vi at trekantene CDB og ADB utgjør trekanten ABC | |||
Areal CDB: $\frac{r \cdot a}{2}$ | |||
Areal: ADB: $\frac{c \cdot r}{2}$ | |||
Kombinerer: | |||
$\frac{r \cdot a}{2}+ \frac{c \cdot r}{2}=\frac {a \cdot b}{2} \\ra + rc = ab \\ r(a+c) =ab$ | |||
===d)=== | ===d)=== | ||
$a \cdot b = (a+c) \cdot r \\ ab =(a+c) \cdot \frac{a(c+a)}{b} \\ ab^2 = (a^2+ac)(c-a)$ | $a \cdot b = (a+c) \cdot r \\ ab =(a+c) \cdot \frac{a(c+a)}{b} \\ ab^2 = (a^2+ac)(c-a) \\ ab^2= a^2c - a^3 + ac^2- a^2c \\ ab^2 = - a^3+ ac^2 \\ a^2 + b^2 = c^2$ | ||
==DEL TO== | ==DEL TO== | ||
==Oppgave 1== | |||
===a)=== | |||
I denne type oppgave kan det være lurt å tegne et valgte, for å ha klarhet i situasjonen. | |||
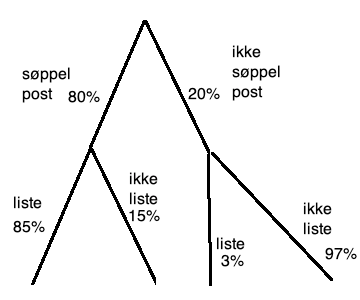
[[File:R1-h19-2-1a.png]] | |||
Sansynlighet spam: $ P(S)$ | |||
Sans. ikke spam : $P( \overline{S})$ | |||
Ord fra liste: L | |||
$P(L) = P(S) \cdot P(L |S) + P( \overline{S}) \cdot P(L | \overline{S}) \\ 0,8 \cdot 0,85 + 0,2 \cdot 0,03 = 0,686$ | |||
eller 68,6% | |||
===b)=== | |||
Tenker gunstige delt på mulige. Ender da opp med Bayes setning. | |||
$P(S|L)= \frac{P(S) \cdot P(L|S )}{P(L)} = \frac{0,68}{0,686}= 0,991$ | |||
eller 99,1% | |||
===c)=== | |||
V skal finne sannsynlighet for søppelpost, når den ikke inneholder ord fra listen: | |||
$P(S | \overline{L}) = \frac{gunstige}{mulige} = \frac{P(S) \cdot P( \overline{L}|S) }{1-P(L)} = \frac{0,8 \cdot 0,15}{1- 0,686 } 0,382$ | |||
eller ca. 38,2% | |||
==Oppgave 2== | |||
===a)=== | |||
$f(x)= -x^3+x^2+kx+2 \\ f'(x) = -3x^2+2x+k$ | |||
Dersom andregradsfunksjonen har to nullpunkt vil den også skifte fortegn slik at f har et bunnpunkt og et toppunkt. For at dette skal være tilfelle må $b^2-4ac$ være positivt: | |||
$4-4(-3)k >0 \\ 4+12k>0 \\ k> \frac 13$ | |||
===b)=== | |||
f har toppunkt i (2, f(2)): | |||
$f'(2)=0 \\ -3 \cdot 2^2 + 2 \cdot 2 +k=0 \\ -12+4+k =0 \\k =8$ | |||
Finner så f(2), når k = 8 : | |||
$f(2) = -3^3+2^2+8 \cdot 2+2 = -8+4+16+2 = 14$ | |||
Toppunkt (2, 14) | |||
Bunnpunkt: | |||
Finner den andre x verdien som gir f'(x) = 0, når k = 8. | |||
Bruker ABC formelen og får x = 2 eller $x = - \frac 43$. 2 er x verdien til toppunktet, og $- \frac 43$ er x verdien til bunnpunktet. Vi finner y koordinaten til punktet ved å finne $f(- \frac 43)$ som gir $- \frac{122}{27}$ | |||
Bunnpunkt $( - \frac{4}{3}, - \frac{122}{27})$ | |||
===c)=== | |||
$ f' \,'(x) = - 6x+2 $ | |||
Setter den dobbelderiverte lik null, for å finne x-koordinaten til vendepunktet. | |||
$-6x+2=0 \\ x= \frac 13$ | |||
Setter $x= \frac 13$ inn i f(x): | |||
$f(- \frac 13) = - ( \frac 13)^3+ \frac 13^2+ \frac 13x+2 =- \frac{1}{27} + \frac{1}{9} + \frac 13k+2 = \frac{56}{27} + \frac 13k$ | |||
Vendepunkt $ ( \frac 13, \frac{56}{27} + \frac 13k)$ | |||
Da kjenner vi vendepunktet. Vi setter inn x koordinaten i uttrykket til den DERIVERTE, og setter det lik 2: | |||
$-3( \frac 13)^2+2 \cdot \frac 13 + k =2 \\ k= \frac 53$ | |||
==Oppgave 3== | |||
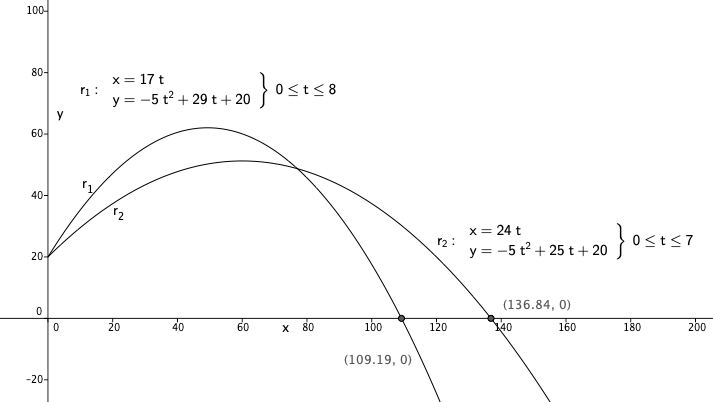
===a)=== | |||
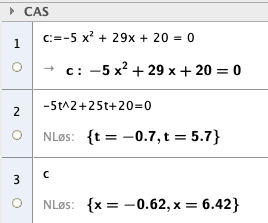
Ballene er i luften i henholdsvis 6,4 og 5,7 sekunder. | |||
[[File:R1-h19-2-3a2.png]] | |||
===b)=== | |||
[[File:R1-h19-2-3b.png]] | |||
===c)=== | |||
[[File:R1-h19-2-3c.png]] | |||
Banefarten er henholdsvis 33,6 og 34,7 m/s idet ballene forlater taket. | |||
===d)=== | |||
[[File:R1-h19-2-3d.png]] | |||
Ballene har skaffe fartsrettnmng etter 3,87 sekunder. Da er forholdet mellom x og y komponentene til begge vektorene den samme. Vinkelen mellom vektor og x-aksen er ca. - 30 grader. | |||
==Oppgave 4== | |||
===a)=== | |||
[[File:R1-h19-2-4a.png]] | |||
Skriver inn funksjonen f, og punktene P og Q. Bruker linjefunksjonen og får et uttrykk for linjen gjennom P og Q. Setter denne linjen lik f og får x koordinatene til R og Q | |||
===b)=== | |||
Her viser vi at stigningstallene til tangentene multiplisert blir -1- Da står linjene normalt på hverandre. Du kan også bruke skalarprodukt. | |||
[[File:R1-h19-2-4b.png]] | |||
Siste sideversjon per 8. nov. 2021 kl. 19:25
Diskusjon av oppgaven på matteprat
Løsningsforslag del 2 fra Kristian Saug
Løsningsforslag (pdf) fra joes
Løsningsforslag fra Svein Arneson
Løsning del 1 som video av Lektor Håkon Raustøl
Løsning del 2 som video av Lektor Håkon Raustøl
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
a)
$$ f(x)=x^4-2x+ln(x) \\ f'(x)= 4x^3-2+ \frac 1x$$
b)
$ g(x)= x^7e^x \\ g'(x) = 7x^6e^x + x^7e^x = e^xx^6(7+x) $
c)
$h(x)= \frac{ln(2x)}{x^2} \\ h'(x) = \frac{\frac{1}{2x} \cdot 2 \cdot x^2-2 \cdot x \cdot ln(2x)}{x^4} \\ h'(x)= \frac{1- 2 ln(2x)}{x^3}$
Oppgave 2
$4(ln(a \cdot b^3))-3(ln(a\cdot b^2))-ln(\frac ab) \\ 4 ln(a) + 12 ln(b) - 3ln(a) - 6 ln(b) - ln (a) + ln(b) = 7 ln (b)$
Oppgave 3
a)
Dersom P(x) skal deles på (x-2) og gå opp. må P(x) = 0, dvs. P(2) = 0
$P(2) = 0 \\ 2^3+ 6 \cdot 2^2 + k\cdot 2 -30 =0 \\ 8+24+2k-30=0 \\ k=-1$
b)
Bruker så ABC formel på svaret og får:
$ x^2 + 8x + 15 = 0 \\ x = \frac{-8 \pm \sqrt{64-4 \cdot 1 \cdot 15}}{2} \\ x = \frac{-8 \pm 2}{2} \\ x = -5 \vee x =-3$
Faktorisert form:
$x^3 +6x^2 - x -30 = (x-2)(x+3)(x+5)$
c)
Fra b har vi at:
$(x-2)(x+3)(x+5) \leq 0$
Tegner fortegnsskjema:
$x \in < \leftarrow, -5] \cup [-3,2]$
Oppgave 4
a)
$\vec{AB} = [(2-(-2), -1-1] = [4,-2] \\ \vec{BC} = [(4-2, 2-(-1)]= [2, 3]$
b)
$\vec{AB} \cdot \vec{BC} = [4,-2]\cdot[2,3] = 4 \cdot 2 + (-2) \cdot 3 = 8-6 =2 \neq 0$
To vektorer som er normale på hverandre har skalarprodukt lik null. Disse står ikke 90 grader på hverandre.
c)
$\vec{AD} = [t+2, 2]$
Bruker skalarprodukt igjen:
$ \vec{AB} \cdot \vec{AD} = 0 \\ [4,-2] \cdot [t +2,2] =0 \\ 4t + 8 - 4 =0 \\ t = -1$
d)
Et trapes er en firkant der to sider er parallelle. Det kan her skje på to måter:
$\vec{AB} \parallel\vec{CD}$
eller
$\vec{BC} \parallel\vec{DA}$
Vi sjekker begge mulighetene.
$\vec{AB} \parallel\vec{CD} \\ \vec{AB} = k \vec{CD} \\ [4,-2] = k [t-4, 1] \\ 4 = kt-4k \wedge -2 = k \\ t =2$
t = 2 gir ett trapes.
$\vec{BC} \parallel\vec{DA} \\ \vec{BC} = k \vec{DA} \\ [2, 3] = k [-2-t,-2] \\ 2=-2k-kt \wedge 3=-2k \\ k = - \frac 32 \wedge 2 =3 + \frac 32 t \\ t= - \frac 23$
$t = - \frac 23$ gir også et trapes.
Oppgave 5
a)
$\binom{7}{3} \cdot \binom{5}{2} = \frac{7\cdot6\cdot5}{3\cdot2\cdot1}\cdot\frac{5\cdot4}{2\cdot1}=35\cdot10=350$
Det er mulig å sette sammen 350 komiteer.
b)
P(Anne og Jens)$=\frac{3}{7}\cdot\frac{2}{5}=\frac{6}{35}$
Sannsynligheten for at både Anne og Jens blir med i komiteen er $\frac{6}{35}$
c)
P(Anne eller Jens) = P(Anne men ikke jens) + P(Jens men ikke Anne)
$=\frac{3}{7}\cdot\frac{3}{5}+\frac{4}{7}\cdot\frac{2}{5} \\ =\frac{9}{35}+\frac{8}{35}=\frac{17}{35}$
Sannsynligheten for at én av dem blir med i komiteen er $\frac{17}{35}$
Oppgave 6
a)
Diagonal i rektangelet er alltid 2. Arealet er alltid $ A = x \cdot \sqrt{4-x^2} $. Brukte pytagoras for å finne lengden av OC.
Areal av skravert område blir da
$A_{skravert} = \frac 14 \pi \cdot2^2 - x \cdot \sqrt{4-x^2} = \pi - x \sqrt{4-x^2}$
b)
Deriverer F(x) og finner maksimumspunktet:
$F'(x) = \\ ( \pi - x \sqrt{4-x^2})' = \\ -(1 \cdot \sqrt{4-x^2} + x \cdot (-2x) \frac 12 (4-x^2)^{- \frac 12}) = \\ -( \sqrt{4-x^2} - \frac{x^2}{ \sqrt{4-x^2}} ) = \\ - ( \frac{(\sqrt{4-x^2})(\sqrt{4-x^2})}{(\sqrt{4-x^2})} -\frac{x^2}{ \sqrt{4-x^2}} ) = \\ - \frac{4-2x^2}{\sqrt{4-x^2}} = \\ \frac{2(x-\sqrt{2}(x+\sqrt{2})}{\sqrt{4-x^2}}$
Av uttrykket ser vi at $x= \sqrt 2$ gir den deriverte lik null. Dette stemmer også med hva vi vet om største areal av en rektangulær firkant med gitt omkrets, den hvite firkanten vil være et kvadrat.
Oppgave 7
a)
CB er like lang som EB fordi begge linjestykker tangerer samme sirkelsektor ( i C og E).
b)
Begge trekantene har en felles vinkel i A. Begge trekanten har en vinkel på 90 grader (i C og E). Trekantene er derfor formlike.
Bruker formlikhet:
$\frac{c-a}{r} = \frac{b}{c} \\ r = \frac{a(c-a)}{b} $
c)
Trekanten ABC har areal: $A= \frac {a \cdot b}{2}$
Fra figuren ser vi at trekantene CDB og ADB utgjør trekanten ABC
Areal CDB: $\frac{r \cdot a}{2}$
Areal: ADB: $\frac{c \cdot r}{2}$
Kombinerer:
$\frac{r \cdot a}{2}+ \frac{c \cdot r}{2}=\frac {a \cdot b}{2} \\ra + rc = ab \\ r(a+c) =ab$
d)
$a \cdot b = (a+c) \cdot r \\ ab =(a+c) \cdot \frac{a(c+a)}{b} \\ ab^2 = (a^2+ac)(c-a) \\ ab^2= a^2c - a^3 + ac^2- a^2c \\ ab^2 = - a^3+ ac^2 \\ a^2 + b^2 = c^2$
DEL TO
Oppgave 1
a)
I denne type oppgave kan det være lurt å tegne et valgte, for å ha klarhet i situasjonen.
Sansynlighet spam: $ P(S)$
Sans. ikke spam : $P( \overline{S})$
Ord fra liste: L
$P(L) = P(S) \cdot P(L |S) + P( \overline{S}) \cdot P(L | \overline{S}) \\ 0,8 \cdot 0,85 + 0,2 \cdot 0,03 = 0,686$
eller 68,6%
b)
Tenker gunstige delt på mulige. Ender da opp med Bayes setning.
$P(S|L)= \frac{P(S) \cdot P(L|S )}{P(L)} = \frac{0,68}{0,686}= 0,991$
eller 99,1%
c)
V skal finne sannsynlighet for søppelpost, når den ikke inneholder ord fra listen:
$P(S | \overline{L}) = \frac{gunstige}{mulige} = \frac{P(S) \cdot P( \overline{L}|S) }{1-P(L)} = \frac{0,8 \cdot 0,15}{1- 0,686 } 0,382$
eller ca. 38,2%
Oppgave 2
a)
$f(x)= -x^3+x^2+kx+2 \\ f'(x) = -3x^2+2x+k$
Dersom andregradsfunksjonen har to nullpunkt vil den også skifte fortegn slik at f har et bunnpunkt og et toppunkt. For at dette skal være tilfelle må $b^2-4ac$ være positivt:
$4-4(-3)k >0 \\ 4+12k>0 \\ k> \frac 13$
b)
f har toppunkt i (2, f(2)):
$f'(2)=0 \\ -3 \cdot 2^2 + 2 \cdot 2 +k=0 \\ -12+4+k =0 \\k =8$
Finner så f(2), når k = 8 :
$f(2) = -3^3+2^2+8 \cdot 2+2 = -8+4+16+2 = 14$
Toppunkt (2, 14)
Bunnpunkt:
Finner den andre x verdien som gir f'(x) = 0, når k = 8.
Bruker ABC formelen og får x = 2 eller $x = - \frac 43$. 2 er x verdien til toppunktet, og $- \frac 43$ er x verdien til bunnpunktet. Vi finner y koordinaten til punktet ved å finne $f(- \frac 43)$ som gir $- \frac{122}{27}$
Bunnpunkt $( - \frac{4}{3}, - \frac{122}{27})$
c)
$ f' \,'(x) = - 6x+2 $
Setter den dobbelderiverte lik null, for å finne x-koordinaten til vendepunktet.
$-6x+2=0 \\ x= \frac 13$
Setter $x= \frac 13$ inn i f(x):
$f(- \frac 13) = - ( \frac 13)^3+ \frac 13^2+ \frac 13x+2 =- \frac{1}{27} + \frac{1}{9} + \frac 13k+2 = \frac{56}{27} + \frac 13k$
Vendepunkt $ ( \frac 13, \frac{56}{27} + \frac 13k)$
Da kjenner vi vendepunktet. Vi setter inn x koordinaten i uttrykket til den DERIVERTE, og setter det lik 2:
$-3( \frac 13)^2+2 \cdot \frac 13 + k =2 \\ k= \frac 53$
Oppgave 3
a)
Ballene er i luften i henholdsvis 6,4 og 5,7 sekunder.
b)
c)
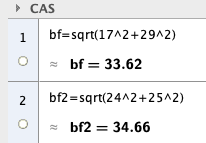
Banefarten er henholdsvis 33,6 og 34,7 m/s idet ballene forlater taket.
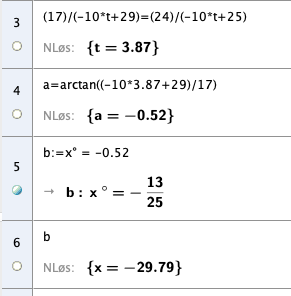
d)
Ballene har skaffe fartsrettnmng etter 3,87 sekunder. Da er forholdet mellom x og y komponentene til begge vektorene den samme. Vinkelen mellom vektor og x-aksen er ca. - 30 grader.
Oppgave 4
a)
Skriver inn funksjonen f, og punktene P og Q. Bruker linjefunksjonen og får et uttrykk for linjen gjennom P og Q. Setter denne linjen lik f og får x koordinatene til R og Q
b)
Her viser vi at stigningstallene til tangentene multiplisert blir -1- Da står linjene normalt på hverandre. Du kan også bruke skalarprodukt.