S1 2019 vår LØSNING: Forskjell mellom sideversjoner
| (82 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 7: | Linje 7: | ||
=DEL EN= | |||
==Oppgave 1== | ==Oppgave 1== | ||
| Linje 13: | Linje 13: | ||
===a)=== | ===a)=== | ||
$3^{x-5} = 81 \\ 3^{x-5} = 3^4 | $3^{x-5} = 81 \\ 3^{x-5} = 3^4 \\ x-5 = 4 \\ x=9 $ | ||
===b)=== | ===b)=== | ||
$x^2-7x+10 =0$ | |||
Faktoriserer | |||
$x^2-7x+10 = (x-2)(x-5)$ | |||
Finner nullpunktene: | |||
$(x-2)(x-5)=0 \\ x=2 \vee x = 5$ | |||
Kan også bruke abc - formelen for faktorisering. | |||
===c)=== | ===c)=== | ||
$lg(x+3) - lgx = 1 \quad x>0 \\ lg ( \frac{x+3}{x} )= 1 \\ 10^{lg(\frac {x+3}{x} )}= 10^1 \\ \frac{x+3}{x} = 10 \\ x+3 = 10x \\ 9x = 3 \\ x = \frac{1}{3}$ | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | ===a)=== | ||
$ \frac{16^2 \cdot 27^3}{72^2 \cdot 12} \\= \frac{(2^4)^2 \cdot (3^3)^3}{(2^3\cdot 3^2)^2 \cdot 2^2 \cdot 3 } \\ = \frac{2^8 \cdot 3^9}{2^6 \cdot 3^4 \cdot 2^2 \cdot 3} \\ = \frac{2^8 \cdot 3^9}{2^8 \cdot 3^5} \\ = 2^{8-8} \cdot 3^{9-5} = 2^0 \cdot 3^4 = 3^4 = 81$ | |||
===b)=== | ===b)=== | ||
$ \frac{x-2}{x-1} - \frac{x}{x+1} - \frac{2x}{x^2-1} \\ =\frac{(x-2) \cdot \color{red}{ (x+1)}}{(x-1) \cdot \color{red}{ (x+1)}} - \frac{x \cdot \color{red}{ (x-1)}}{(x+1) \cdot \color{red}{ (x-1)}} - \frac{2x}{(x+1)(x-1)} \\= \frac{(x^2+x-2x-2) - (x^2-x) - 2x}{(x-1)(x+1)} \\= \frac{x^2+x-2x-2-x^2+x-2x}{(x-1)(x+1)} \\ = \frac{-2x-2}{(x-1)(x+1)} \\ = \frac{-2(x+1)}{(x-1)(x+1)} \\ = - \frac{2}{x-1}$ | |||
===c)=== | ===c)=== | ||
$lg( \frac{2}{x^2}) + lg (2x^2) + lg(x) - lg (4x) \\ =( lg(2) - lg(x^2)) + ( lg (2) + lg(x^2)) + lg(x) - (lg(4) + lg(x)) \\= lg(2) - 2lg(x) +lg(2) + 2lg(x) + lg(x)- lg(2^2) - lg(x) \\ = 2 lg(2) + lg(x) -2lg(2) - lg(x) \\ = 0 $ | |||
==Oppgave 3== | ==Oppgave 3== | ||
<math> \left[ \begin{align*} x^2+2y =13x \\ 3x - y =-5 \end{align*}\right] </math> | |||
Løser andre likning og setter inn i den første. | |||
$ y = 3x + 5$ | |||
Vi setter inn for y i den første likningen: | |||
$x^2 + 2 (3x + 5) = 13x \\ x^2 + 6x+10 = 13x \\x^2 -7x + 10 = 0$ | |||
Fra oppgave 1b) har vi at $x_1=2$ og $x_2=5$ | |||
Fra andre likning har vi: | |||
$y_1=3\cdot2+5=11$ | |||
$y_2=3\cdot 5+5=20$ | |||
Løsning: $x_1=2$, $y_1=11$ og $x_2=5$, $y_2=20$ | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
Pris brus = x og pris pølse = y. | |||
<math> \left[ \begin{align*} 6x + 4y =170 \\ 5x + 10y =275 \end{align*}\right] </math> | |||
===b)=== | |||
Løser likning II med hensyn på x: | |||
$5x=275-10y \\ x = 55 - 2y $ | |||
setter så uttrykket for x inn i likning I: | |||
$6( 55 - 2y) +4y =170 \\ 330 -12y + 4y = 170 \\ -8y = -160 \\ y = 20$ | |||
Setter inn y=20 i likning II: | |||
$x= 55-2\cdot 20=55-40=15$ | |||
En brus koster 15 kroner og en pølse koster 20 kroner. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
$ f(x) = x^3+3x \\ f ' (x) = 3x^2+3 \\ f '(1) = 3 \cdot 1 + 3 = 6 $ | |||
Når x =1 har funksjonen en momentan vekstfart på 6. | |||
===b)=== | |||
Den deriverte er positiv for alle verdier av x, derfor er funksjonen voksende og har kun positive tangenter. | |||
===c)=== | |||
$ f ' (x) = 15 \\ 3x^2+3 = 15 \\ 3x^2 = 12 \\ x^2 = 4 \\ x= \pm 2 $ | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
$\binom{10}{3} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 4 = 120 $ | |||
120 ulike grupper på tre deltakere kan komme til finalen. | |||
===b)=== | |||
Vi har flere kvinner enn menn i en gruppe på tre, dersom vi har to eller tre kvinner. | |||
P(to eller tre kvinner) = $\frac{\binom{5}{2} \binom{5}{1}}{ \binom{10}{3}} + \frac{\binom{5}{3} \binom{5}{0}}{ \binom{10}{3}} = \frac{10 \cdot 5}{120} + \frac{10 \cdot 1 }{120} = \frac{60}{120} = \frac{1}{2}$ | |||
60 av de 120 gruppene, det vil si halvparten, inneholder flere kvinner enn menn. | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
Ulikhetene som begrenser området: | |||
$x \geq 0$ | |||
$y \geq 0$ | |||
$y \leq 0,5x+2$ | |||
$y \leq -2x+6$ | |||
===b)=== | |||
Finner skjæringspunktene for de to linjene: | |||
$0,5x+2=-2x+6 \\ 2,5x=4 \\ x=\frac{4}{2,5} =\frac{16}{10}=1,6$ | |||
$y= 0,5\cdot 1,6+2=0,8+2=2,8$ | |||
Sjekker hjørnene i område for den største verdien av $3x+y$ | |||
$(1.6,2.8) \Rightarrow 3\cdot 1.6+2.8=4.8+2.8=7.6$ | |||
$(0,2) \Rightarrow 3\cdot 0+2=2$ | |||
$(3,0) \Rightarrow 3\cdot 3+0=9$ | |||
Den største verdien størrelsen $3x+y$ kan ha innenfor det blå området er 9.. | |||
===c)=== | |||
$(0,2)$ satt inn i størrelsen $y-a\cdot x$ gir verdien $2-a\cdot 0 = 2$ | |||
Verdien av $a$ må være slik at de andre to hjørnene ikke får en verdi større enn 2. | |||
For hjørnet $(3,0)$ får vi verdien $0-a\cdot 3=-3a$. Vi har $-3a < 2 $ for alle $a > -\frac{2}{3}$ | |||
For hjørnet $(1.6,2.8)$ får vi verdien $2.8-a\cdot 1.6$. | |||
$2.8-a\cdot 1.6 < 2 \\ -1.6a < -0.8 \\ a>0,5 $ | |||
Vi må ha $a>0,5$ for at størrelsen $y-a\cdot x$ skal ha størst verdi i $(0,2)$. | |||
==Oppgave 8== | ==Oppgave 8== | ||
==DEL TO== | ===a)=== | ||
Omkrets: $ O = 4y +8x = 12 \\ 4y = 12 - 8x \\ y= 3-2x$ | |||
Areal: $A= y^2+2x^2 \\ A(x)= (3-2x)^2+2x^2 \\ A(x)= 9-12x+4x^2+2x^2 \\ A(x)= 6x^2-12x +9$ | |||
===b)=== | |||
$A' (x)= 12x -12 \\ A' (x)=0 \\ 12x-12 =0 \\ x=1 \\ $ | |||
Innsatt for y: $y = 3 - 2x \\ y = 3 - 2 \cdot 1 \\ y=1$ | |||
Det minste arealet får man når både x = 1 og y = 1. | |||
=DEL TO= | |||
==Oppgave 1== | |||
===a)=== | |||
Vi har $x\geq 0$ og $y \geq 0$ fordi bakeren må lage 0 eller flere kaker. Han kan ikke lage et negativt antall kaker. | |||
La x være antall kaker av type A, og y være antall kaker av type B. | |||
For mel har vi: | |||
$300x+500y \leq 50000 \\ \frac{300}{100}x+\frac{500}{100}y \leq \frac{50000}{100} \\ 3x+5y\leq 500$ | |||
For sukker har vi: | |||
$100x+50y\leq 7000 \\ \frac{100}{50}x+\frac{50}{50}y\leq \frac{7000}{50} \\ 2x+y \leq 140$ | |||
For smør har vi: | |||
$125x+50y\leq 8500 \\ \frac{125}{25}x+\frac{50}{25}y \leq \frac{8500}{25}\\ 5x+2y \leq 340$ | |||
===b)=== | |||
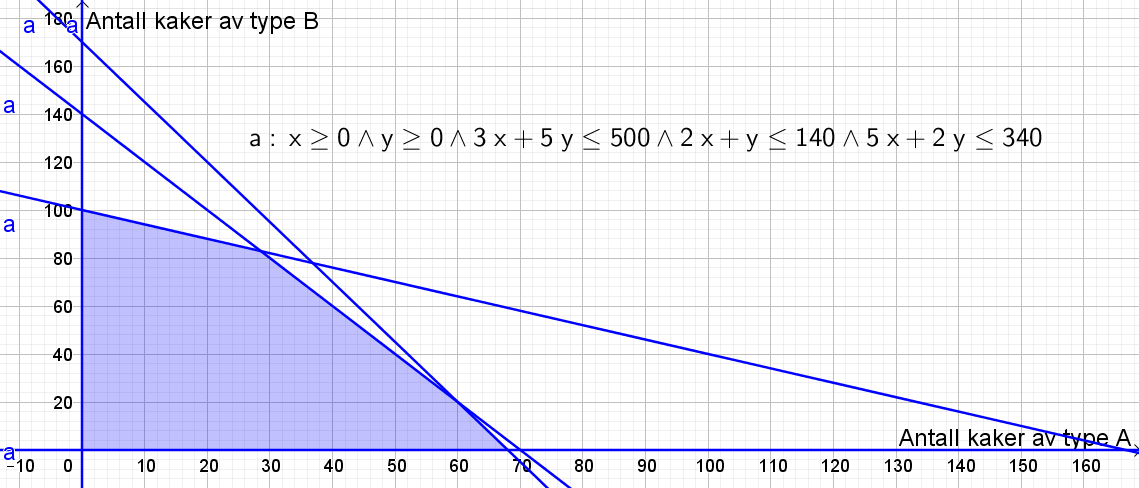
Bruker Geogebra og legger inn ulikhetene. | |||
[[File: oppg1.png]] | |||
===c)=== | |||
Fortjenesten er gitt ved: $I(x,y)=160x+120y$ | |||
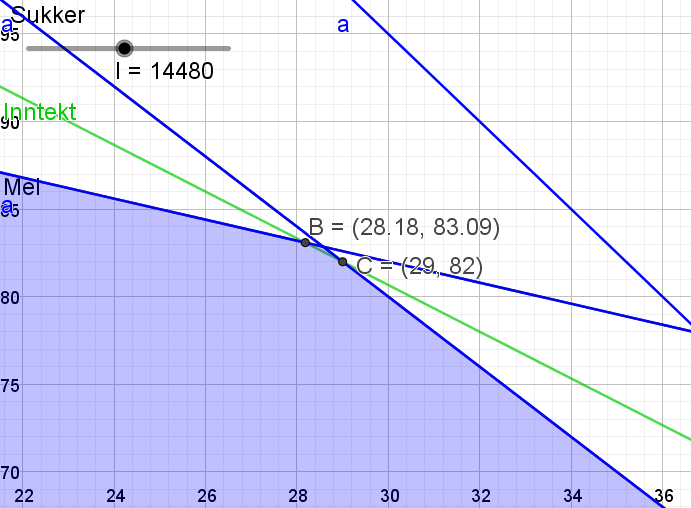
Legger inn en glider for fortjenesten i Geogebra. Lager "skjæring mellom to objekt" mellom linjen $3x+5y=500$ og glideren (gir punkt B), samt mellom linjen $2x+y=140$ og glideren (gir punkt C). Ved hjelp av glideren finner jeg antall hele kaker som gir maksimal fortjeneste. | |||
[[File: oppg1b2-del2.png]] | |||
Bakermester Snipp må bake 29 kaker av type A og 82 kaker av type B. Fortjenesten blir da $160\cdot 29 + 120\cdot 82=14480$ kr. | |||
===d)=== | |||
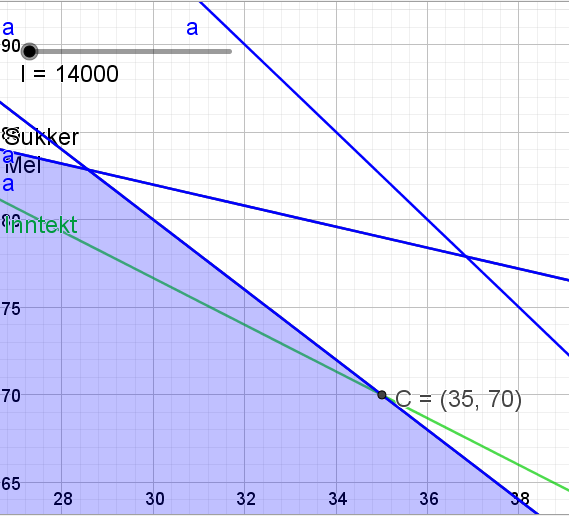
Bruker glideren fra oppgave c) og beveger den ned til punktet C=(35,70), der hvor det lages 70 kaker av type B. Fortjenesten blir da $160\cdot 35 + 120\cdot 70=14000$ kr. | |||
[[File: oppg1d-del2.png]] | |||
==Oppgave 2== | |||
===a)=== | |||
Bruker regresjonsanalyse i Geogebra. | |||
[[File: oppg2-del2.png]] | |||
Eksponentialfunksjonen $Q(x)= 1504\cdot 0,994^x$ passer best med tallene i tabellen. | |||
===b)=== | |||
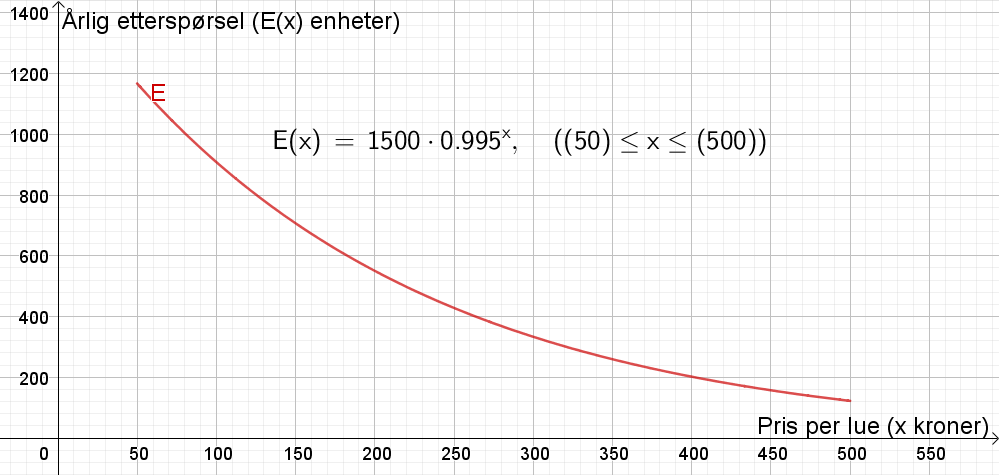
[[File: oppg2b-del2.png]] | |||
===c)=== | |||
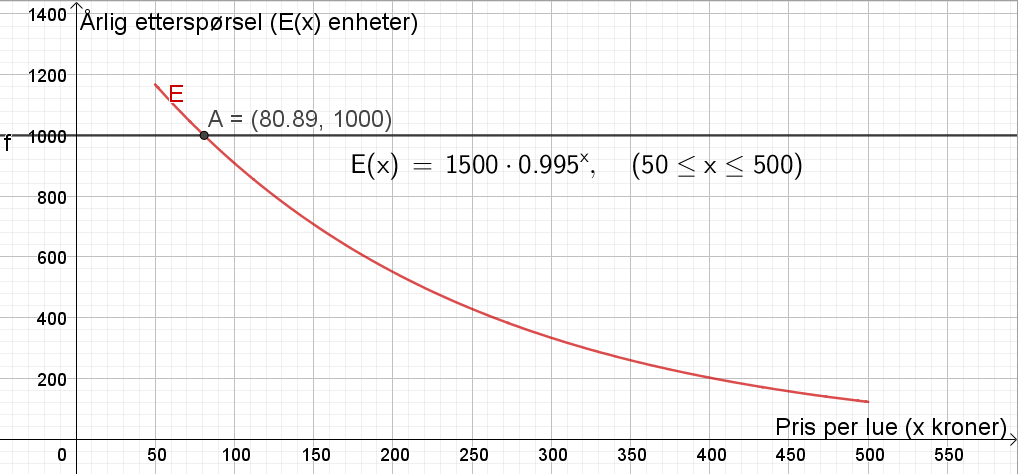
Lager linjen y=1000 og bruker "Skjæring mellom to objekt" mellom denne linjen og grafen til E. Får punkt A=(80.89, 1000). | |||
[[File: oppg2c-del2.png]] | |||
Det betyr at prisen per lue må være maksimalt 80.89 kroner (eller 80 kroner) for at etterspørselen skal være på mer enn 1000 luer per år. | |||
===d)=== | |||
Lager en funksjon for inntekten, hvor inntekten er lik etterspørsel ganger pris per lue: $I(x)=E(x)\cdot x$ | |||
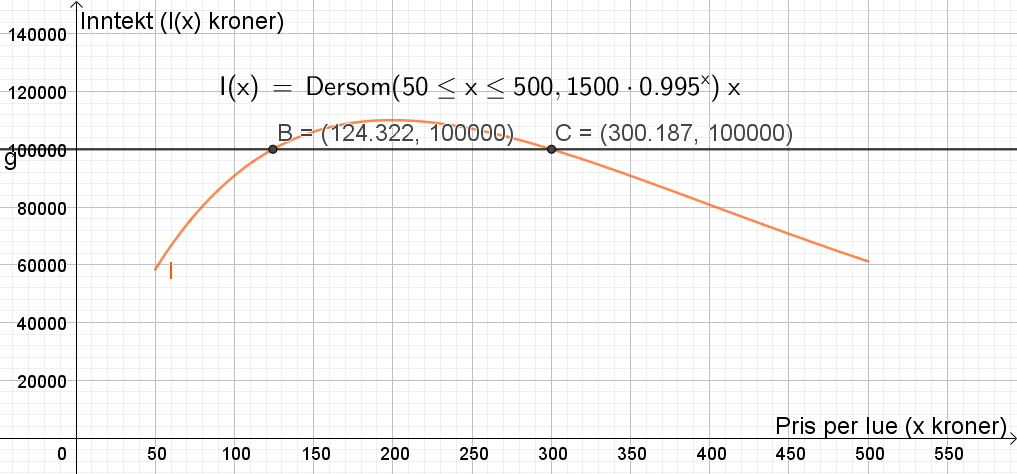
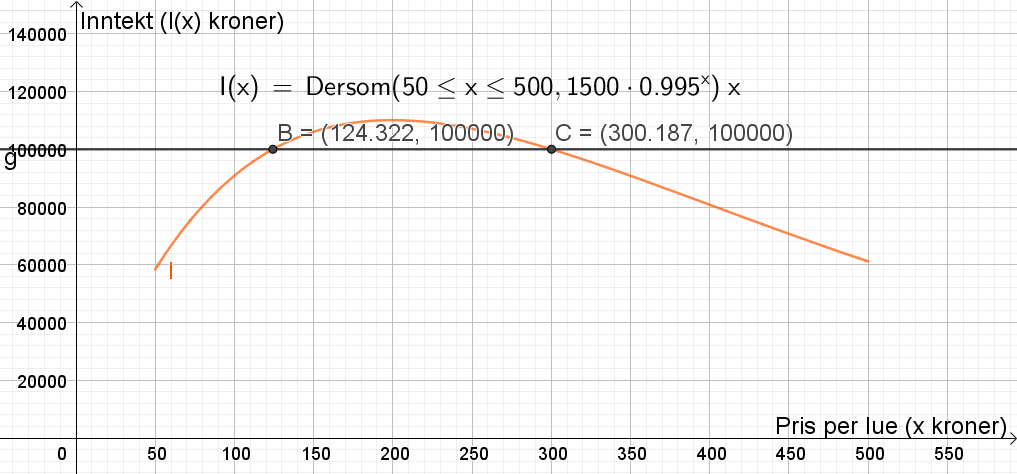
Tegner grafen til I(x) i Geogebra. Lager linjen y=100000 og bruker "Skjæring mellom to objekt" mellom denne linjen og grafen til I(x). Får punktene B=(124.3, 100000) og C=(300.2, 100000). | |||
[[File: S1V2019-oppg2d-del2.png]] | |||
For å selge luer for til sammen 100 000 kr, må bedriften prise luene til ca. 124 kr per lue eller 300 kr per lue. Imidlertid kan bedriften tjene enda mer dersom den priser luene mellom 124 kr og 300 kr. | |||
==Oppgave 3== | |||
===a)=== | |||
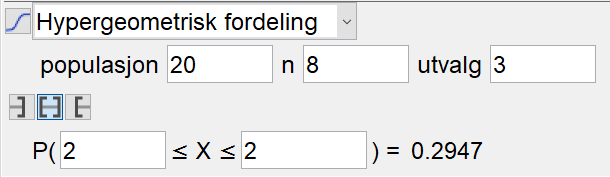
Bruker sannsynlighetskalkulatoren i Geogebra, og velger hypergeometrisk fordeling. 8 av de 20 ansatte er menn, og utvalget er 3. | |||
[[File: oppg3a-del2-S1-V2019.png]] | |||
Sannsynligheten for at nøyaktig 2 av de 3 vinnerne er menn, er 0,2947. | |||
===b)=== | |||
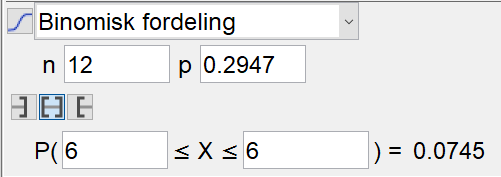
Velger binomisk fordeling, der antall lotterier er 12, og sannsynligheten for at 2 av 3 vinnere er menn, er 02947 (fra forrige oppgave). | |||
[[File: oppg3b-del2-S1-vår2019.png]] | |||
Sannsynligheten for at 2 av 3 vinnere er menn i 6 av de 12 lotteriene, er 0,0745 = 7,45%. | |||
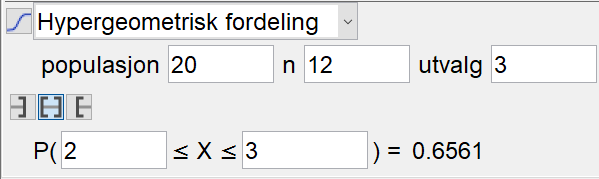
===c)=== | |||
Finner først sannsynligheten for at flertallet av vinnere er kvinner i ett lotteri. Sannsynligheten er 0,6561. | |||
[[File: oppg3c1-del2-S1V19.png]] | |||
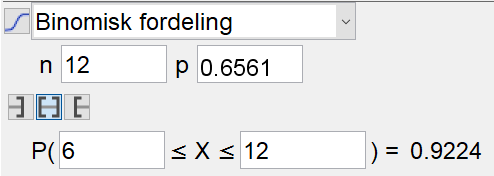
Finner deretter sannsynligheten for at flertallet av vinnerne er kvinner i minst halvparten av lotteriene. | |||
[[File: oppg3c2-del2-S1V19.png]] | |||
Sannsynligheten er 0,9224 = 92,24 %. | |||
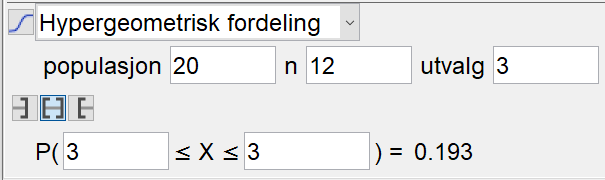
===d)=== | |||
Sannsynligheten for at alle vinnerne i ett lotteri er kvinner er 0,193. | |||
[[File: oppg3kvinner-del2-S1V19.png]] | |||
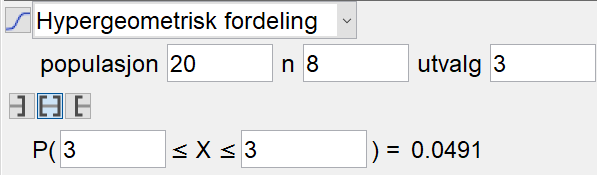
Sannsynligheten for at alle vinnerne i ett lotteri er menn er 0,0491. | |||
[[File: oppg3menn-del-S1V19.png]] | |||
Sannsynligheten for at alle vinnerne er av samme kjønn i ett lotteri er da $0,193+0,0491=0,2421$ | |||
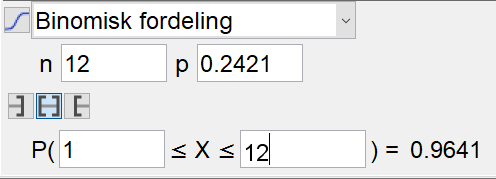
Finner sannsynligheten for at de tre vinnerne har samme kjønn i minst ett av de tolv lotteriene: | |||
[[File: oppg3d-del2-S1V19.png]] | |||
Sannsynligheten er 0,9641 = 96,41%. | |||
Siste sideversjon per 31. des. 2019 kl. 11:47
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
a)
$3^{x-5} = 81 \\ 3^{x-5} = 3^4 \\ x-5 = 4 \\ x=9 $
b)
$x^2-7x+10 =0$
Faktoriserer
$x^2-7x+10 = (x-2)(x-5)$
Finner nullpunktene:
$(x-2)(x-5)=0 \\ x=2 \vee x = 5$
Kan også bruke abc - formelen for faktorisering.
c)
$lg(x+3) - lgx = 1 \quad x>0 \\ lg ( \frac{x+3}{x} )= 1 \\ 10^{lg(\frac {x+3}{x} )}= 10^1 \\ \frac{x+3}{x} = 10 \\ x+3 = 10x \\ 9x = 3 \\ x = \frac{1}{3}$
Oppgave 2
a)
$ \frac{16^2 \cdot 27^3}{72^2 \cdot 12} \\= \frac{(2^4)^2 \cdot (3^3)^3}{(2^3\cdot 3^2)^2 \cdot 2^2 \cdot 3 } \\ = \frac{2^8 \cdot 3^9}{2^6 \cdot 3^4 \cdot 2^2 \cdot 3} \\ = \frac{2^8 \cdot 3^9}{2^8 \cdot 3^5} \\ = 2^{8-8} \cdot 3^{9-5} = 2^0 \cdot 3^4 = 3^4 = 81$
b)
$ \frac{x-2}{x-1} - \frac{x}{x+1} - \frac{2x}{x^2-1} \\ =\frac{(x-2) \cdot \color{red}{ (x+1)}}{(x-1) \cdot \color{red}{ (x+1)}} - \frac{x \cdot \color{red}{ (x-1)}}{(x+1) \cdot \color{red}{ (x-1)}} - \frac{2x}{(x+1)(x-1)} \\= \frac{(x^2+x-2x-2) - (x^2-x) - 2x}{(x-1)(x+1)} \\= \frac{x^2+x-2x-2-x^2+x-2x}{(x-1)(x+1)} \\ = \frac{-2x-2}{(x-1)(x+1)} \\ = \frac{-2(x+1)}{(x-1)(x+1)} \\ = - \frac{2}{x-1}$
c)
$lg( \frac{2}{x^2}) + lg (2x^2) + lg(x) - lg (4x) \\ =( lg(2) - lg(x^2)) + ( lg (2) + lg(x^2)) + lg(x) - (lg(4) + lg(x)) \\= lg(2) - 2lg(x) +lg(2) + 2lg(x) + lg(x)- lg(2^2) - lg(x) \\ = 2 lg(2) + lg(x) -2lg(2) - lg(x) \\ = 0 $
Oppgave 3
<math> \left[ \begin{align*} x^2+2y =13x \\ 3x - y =-5 \end{align*}\right] </math>
Løser andre likning og setter inn i den første.
$ y = 3x + 5$
Vi setter inn for y i den første likningen:
$x^2 + 2 (3x + 5) = 13x \\ x^2 + 6x+10 = 13x \\x^2 -7x + 10 = 0$
Fra oppgave 1b) har vi at $x_1=2$ og $x_2=5$
Fra andre likning har vi:
$y_1=3\cdot2+5=11$
$y_2=3\cdot 5+5=20$
Løsning: $x_1=2$, $y_1=11$ og $x_2=5$, $y_2=20$
Oppgave 4
a)
Pris brus = x og pris pølse = y.
<math> \left[ \begin{align*} 6x + 4y =170 \\ 5x + 10y =275 \end{align*}\right] </math>
b)
Løser likning II med hensyn på x:
$5x=275-10y \\ x = 55 - 2y $
setter så uttrykket for x inn i likning I:
$6( 55 - 2y) +4y =170 \\ 330 -12y + 4y = 170 \\ -8y = -160 \\ y = 20$
Setter inn y=20 i likning II:
$x= 55-2\cdot 20=55-40=15$
En brus koster 15 kroner og en pølse koster 20 kroner.
Oppgave 5
a)
$ f(x) = x^3+3x \\ f ' (x) = 3x^2+3 \\ f '(1) = 3 \cdot 1 + 3 = 6 $
Når x =1 har funksjonen en momentan vekstfart på 6.
b)
Den deriverte er positiv for alle verdier av x, derfor er funksjonen voksende og har kun positive tangenter.
c)
$ f ' (x) = 15 \\ 3x^2+3 = 15 \\ 3x^2 = 12 \\ x^2 = 4 \\ x= \pm 2 $
Oppgave 6
a)
$\binom{10}{3} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 4 = 120 $
120 ulike grupper på tre deltakere kan komme til finalen.
b)
Vi har flere kvinner enn menn i en gruppe på tre, dersom vi har to eller tre kvinner.
P(to eller tre kvinner) = $\frac{\binom{5}{2} \binom{5}{1}}{ \binom{10}{3}} + \frac{\binom{5}{3} \binom{5}{0}}{ \binom{10}{3}} = \frac{10 \cdot 5}{120} + \frac{10 \cdot 1 }{120} = \frac{60}{120} = \frac{1}{2}$
60 av de 120 gruppene, det vil si halvparten, inneholder flere kvinner enn menn.
Oppgave 7
a)
Ulikhetene som begrenser området:
$x \geq 0$
$y \geq 0$
$y \leq 0,5x+2$
$y \leq -2x+6$
b)
Finner skjæringspunktene for de to linjene:
$0,5x+2=-2x+6 \\ 2,5x=4 \\ x=\frac{4}{2,5} =\frac{16}{10}=1,6$
$y= 0,5\cdot 1,6+2=0,8+2=2,8$
Sjekker hjørnene i område for den største verdien av $3x+y$
$(1.6,2.8) \Rightarrow 3\cdot 1.6+2.8=4.8+2.8=7.6$
$(0,2) \Rightarrow 3\cdot 0+2=2$
$(3,0) \Rightarrow 3\cdot 3+0=9$
Den største verdien størrelsen $3x+y$ kan ha innenfor det blå området er 9..
c)
$(0,2)$ satt inn i størrelsen $y-a\cdot x$ gir verdien $2-a\cdot 0 = 2$
Verdien av $a$ må være slik at de andre to hjørnene ikke får en verdi større enn 2.
For hjørnet $(3,0)$ får vi verdien $0-a\cdot 3=-3a$. Vi har $-3a < 2 $ for alle $a > -\frac{2}{3}$
For hjørnet $(1.6,2.8)$ får vi verdien $2.8-a\cdot 1.6$.
$2.8-a\cdot 1.6 < 2 \\ -1.6a < -0.8 \\ a>0,5 $
Vi må ha $a>0,5$ for at størrelsen $y-a\cdot x$ skal ha størst verdi i $(0,2)$.
Oppgave 8
a)
Omkrets: $ O = 4y +8x = 12 \\ 4y = 12 - 8x \\ y= 3-2x$
Areal: $A= y^2+2x^2 \\ A(x)= (3-2x)^2+2x^2 \\ A(x)= 9-12x+4x^2+2x^2 \\ A(x)= 6x^2-12x +9$
b)
$A' (x)= 12x -12 \\ A' (x)=0 \\ 12x-12 =0 \\ x=1 \\ $
Innsatt for y: $y = 3 - 2x \\ y = 3 - 2 \cdot 1 \\ y=1$
Det minste arealet får man når både x = 1 og y = 1.
DEL TO
Oppgave 1
a)
Vi har $x\geq 0$ og $y \geq 0$ fordi bakeren må lage 0 eller flere kaker. Han kan ikke lage et negativt antall kaker.
La x være antall kaker av type A, og y være antall kaker av type B.
For mel har vi:
$300x+500y \leq 50000 \\ \frac{300}{100}x+\frac{500}{100}y \leq \frac{50000}{100} \\ 3x+5y\leq 500$
For sukker har vi:
$100x+50y\leq 7000 \\ \frac{100}{50}x+\frac{50}{50}y\leq \frac{7000}{50} \\ 2x+y \leq 140$
For smør har vi:
$125x+50y\leq 8500 \\ \frac{125}{25}x+\frac{50}{25}y \leq \frac{8500}{25}\\ 5x+2y \leq 340$
b)
Bruker Geogebra og legger inn ulikhetene.
c)
Fortjenesten er gitt ved: $I(x,y)=160x+120y$
Legger inn en glider for fortjenesten i Geogebra. Lager "skjæring mellom to objekt" mellom linjen $3x+5y=500$ og glideren (gir punkt B), samt mellom linjen $2x+y=140$ og glideren (gir punkt C). Ved hjelp av glideren finner jeg antall hele kaker som gir maksimal fortjeneste.
Bakermester Snipp må bake 29 kaker av type A og 82 kaker av type B. Fortjenesten blir da $160\cdot 29 + 120\cdot 82=14480$ kr.
d)
Bruker glideren fra oppgave c) og beveger den ned til punktet C=(35,70), der hvor det lages 70 kaker av type B. Fortjenesten blir da $160\cdot 35 + 120\cdot 70=14000$ kr.
Oppgave 2
a)
Bruker regresjonsanalyse i Geogebra.
Eksponentialfunksjonen $Q(x)= 1504\cdot 0,994^x$ passer best med tallene i tabellen.
b)
c)
Lager linjen y=1000 og bruker "Skjæring mellom to objekt" mellom denne linjen og grafen til E. Får punkt A=(80.89, 1000).
Det betyr at prisen per lue må være maksimalt 80.89 kroner (eller 80 kroner) for at etterspørselen skal være på mer enn 1000 luer per år.
d)
Lager en funksjon for inntekten, hvor inntekten er lik etterspørsel ganger pris per lue: $I(x)=E(x)\cdot x$
Tegner grafen til I(x) i Geogebra. Lager linjen y=100000 og bruker "Skjæring mellom to objekt" mellom denne linjen og grafen til I(x). Får punktene B=(124.3, 100000) og C=(300.2, 100000).
For å selge luer for til sammen 100 000 kr, må bedriften prise luene til ca. 124 kr per lue eller 300 kr per lue. Imidlertid kan bedriften tjene enda mer dersom den priser luene mellom 124 kr og 300 kr.
Oppgave 3
a)
Bruker sannsynlighetskalkulatoren i Geogebra, og velger hypergeometrisk fordeling. 8 av de 20 ansatte er menn, og utvalget er 3.
Sannsynligheten for at nøyaktig 2 av de 3 vinnerne er menn, er 0,2947.
b)
Velger binomisk fordeling, der antall lotterier er 12, og sannsynligheten for at 2 av 3 vinnere er menn, er 02947 (fra forrige oppgave).
Sannsynligheten for at 2 av 3 vinnere er menn i 6 av de 12 lotteriene, er 0,0745 = 7,45%.
c)
Finner først sannsynligheten for at flertallet av vinnere er kvinner i ett lotteri. Sannsynligheten er 0,6561.
Finner deretter sannsynligheten for at flertallet av vinnerne er kvinner i minst halvparten av lotteriene.
Sannsynligheten er 0,9224 = 92,24 %.
d)
Sannsynligheten for at alle vinnerne i ett lotteri er kvinner er 0,193.
Sannsynligheten for at alle vinnerne i ett lotteri er menn er 0,0491.
Sannsynligheten for at alle vinnerne er av samme kjønn i ett lotteri er da $0,193+0,0491=0,2421$
Finner sannsynligheten for at de tre vinnerne har samme kjønn i minst ett av de tolv lotteriene:
Sannsynligheten er 0,9641 = 96,41%.