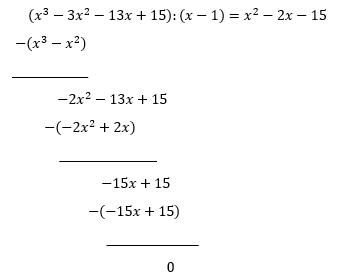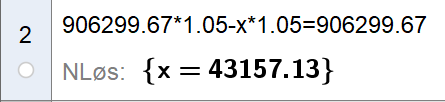S2 2018 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (44 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 2: | Linje 2: | ||
[https://www.matematikk.net/matteprat/viewtopic.php?f=13&t=47620 Diskusjon av denne oppgaven på matteprat] | [https://www.matematikk.net/matteprat/viewtopic.php?f=13&t=47620 Diskusjon av denne oppgaven på matteprat] | ||
[https://www.matematikk.net/matteprat/download/file.php?id=2180 Løsningsforslag laget av LektorNilsen] | |||
[https://github.com/matematikk/vgs_eksamener/blob/master/l%C3%B8sningsforslag/S2/S2_18V/S2_18V_lf.pdf Løsning laget av mattepratbruker Tommy O.] | [https://github.com/matematikk/vgs_eksamener/blob/master/l%C3%B8sningsforslag/S2/S2_18V/S2_18V_lf.pdf Løsning laget av mattepratbruker Tommy O.] | ||
| Linje 193: | Linje 195: | ||
===d)=== | |||
Vi vet at | |||
[[File: S2_V18_del1_6d.png]] | |||
==Oppgave 7== | |||
===a)=== | |||
X er binomisk fordelt fordi: | |||
* Vi har et forsøk med delforsøk (10 delforsøk i dette tilfellet) | |||
* Det er to utfall i delforsøkene: | |||
* | |||
* Delforsøkene er uavhengige av hverandre. Fargen på kulen du trekker i ett delforsøk, påvirker ikke fargen på kulen du trekker i neste delforsøk. | |||
===b)=== | |||
==Oppgave 8== | |||
===a)=== | |||
Sannsynligheten for at et tilfeldig valgt rugbrød veier mellom 0,90 kg og 1,10 kg er 95,45%. | |||
===b)=== | |||
Sannsynligheten for at veksten av rugbrødene på en tilfeldig pall er mellom 99,5 kg og 100,5 kg er ca. 68,3%. | |||
==Oppgave 9== | |||
Et toppunkt for | |||
Et bunnpunkt for | |||
=DEL 2= | =DEL 2= | ||
| Linje 215: | Linje 281: | ||
===b)=== | ===b)=== | ||
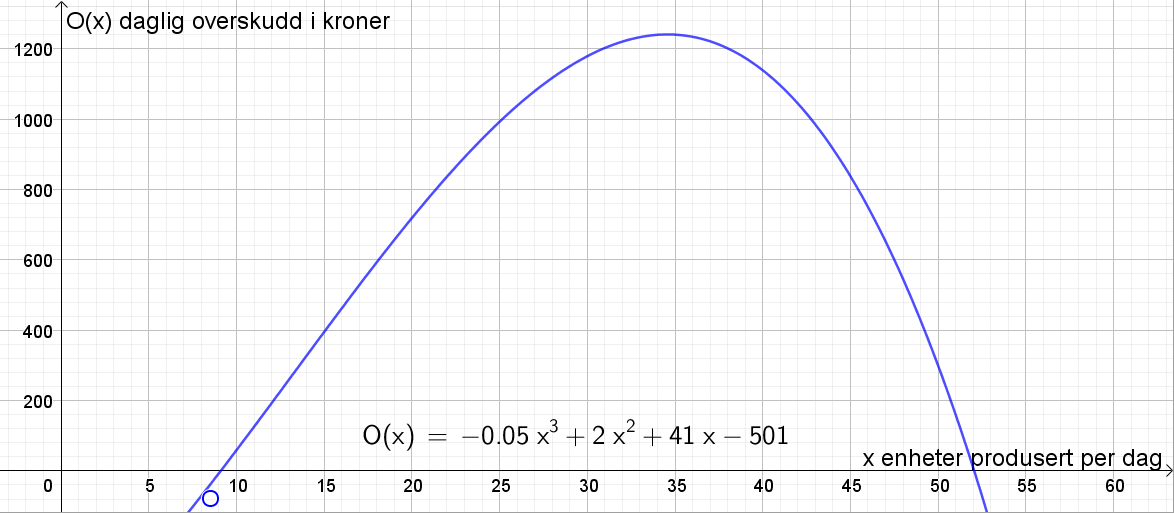
Tegner grafen til O i Geogebra. | |||
[[File: S2_V18_Del2_1b.png]] | |||
===c)=== | |||
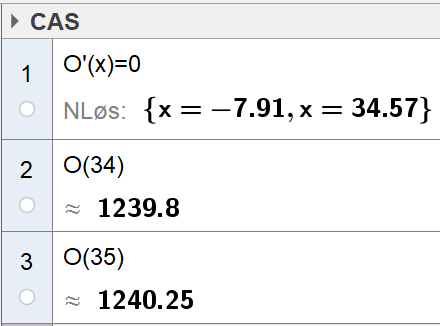
Når grensekostnaden er lik grenseinntekten, har vi det største overskuddet. Bruker CAS til å finne den daglige produksjonsmengden som gir størst overskudd (og altså grensekostnad lik grenseinntekt): | |||
[[File: S2_V18_del2_3c.png]] | |||
Ser av CAS (og grafen tegnet i b) at det er størst overskudd når x=34,57. Det er kun mulig å produsere et heltall antall varer. Sjekker derfor om det er 34 eller 35 antall varer produsert som gir det største overskuddet. Det viser seg at en daglig produksjon på 35 varer gir størst daglig overskudd. | |||
===d)=== | |||
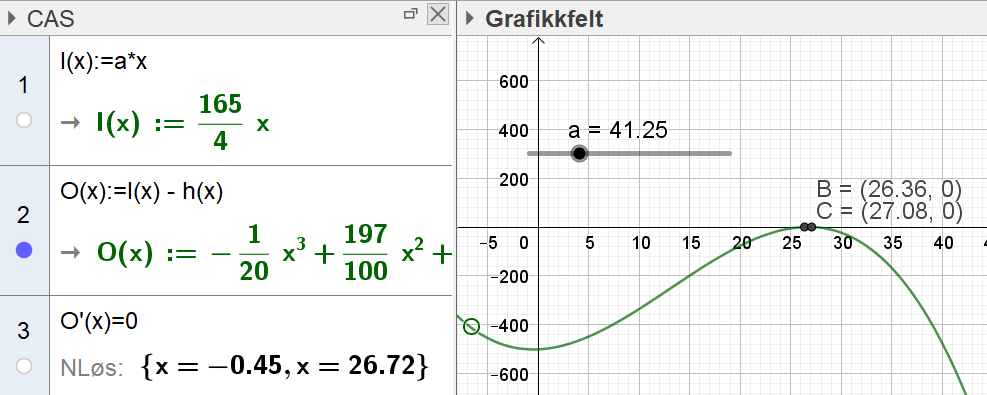
Lager en glider '''a''' for prisen per enhet. Definerer inntekten | |||
[[File: S2_V18_del2_1d.png]] | |||
==Oppgave 2== | |||
===a)=== | |||
Rekke som viser hvor stort beløp Eirik har på kontoen ett år etter siste innbetaling: | |||
Eirik setter ikke inn noen penger på konto det 16. året. Vi har derfor | |||
Regner ut summen av rekken i CAS i Geogebra: | |||
[[File: S2_V18_del2_2a2.png]] | |||
Eirik har 906299,67 kroner på kontoen ett år etter siste innbetaling. | |||
===b)=== | |||
Beløpet etter 15 år, | |||
fordi vi starter med 906299,67 kroner og får 5% rente hvert år, minus en rekke av utbetalinger med tapt renteinntekt for disse utbetalingene. | |||
Utbetalinger, | |||
Etter 15 år skal kontoen være tom, altså | |||
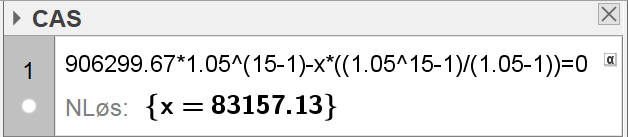
Løser likningen i CAS på Geogebra: | |||
[[File: S2_V18_del2_2b.png]] | |||
Årlig utbetaling blir på 83157,13 kroner. | |||
===c)=== | |||
Vi ønsker alltid at startbeløpet med renter, minus utbetalinger med tapte renter, skal bli lik starbeløpet igjen. Slik kan utbetalingene fortsette evig. Bruker CAS i Geogebra for å løse likningen: | |||
[[File: S2_V18_del2_2c.png]] | |||
Årlig utbetaling blir på 43157,13 kroner. | |||
===d)=== | |||
Bruker nåverdi for å løse denne oppgaven. Summen av nåverdiene i forhold til år 2033 kan skrives som denne rekken: | |||
Bruker CAS i Geogebra til å finne ved hvilket år summen av rekken blir lik antall kroner på konto i 2033. | |||
[[File: S2_V18_del2_2d.png]] | |||
Kontoen er tom når n=19,16. Husk at n=1 tilsvarer år 2033. Det vil si at kontoen er nesten tom ved uttaket 1.juli 2051 (n=19), og helt tom ved siste uttak 1.juli 2052 (n=20). | |||
==Oppgave 3== | |||
===a)=== | |||
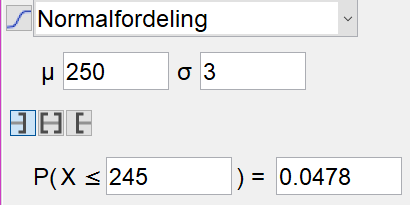
Bruker sannsynlighetskalkulatoren i Geogebra. | |||
[[File:S2_V18_del2_3a.png]] | |||
Sannsynligheten for at en tilfeldig flaske veier for lite er 0,0478, altså 4,78%. | |||
===b)=== | |||
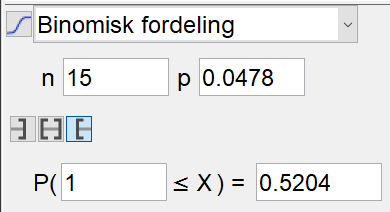
Bruker sannsynlighetskalkulatoren i Geogebra. | |||
[[File:S2_V18_del2_3b.png]] | |||
Sannsynligheten for at en tilfeldig valgt eske skal inneholde én eller flere flasker som veier for lite er 0,5204, dvs 52,04%. | |||
===c)=== | |||
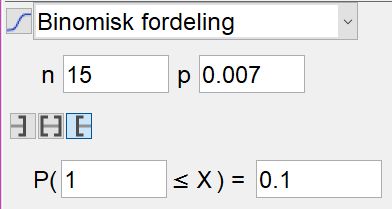
Fortsetter i sannsynlighetskalkulatoren fra oppgave b) og justerer sannsynligheten for at en flaske veier for lite, slik at sannsynligheten for at en tilfeldig valgt eske inneholder én eller flere flasker som veier for lite blir 0,10 (altså 10%). | |||
[[File: S2_V18_del2_3c2.png]] | |||
Ser at sannsynligheten for at en flakse veier for lite i så fall må være 0,007, dvs 0,70%. | |||
===d)=== | |||
Tar opp sannsynlighetskalkulatoren fra oppgave a) og justerer forventningsverdien slik at sannsynligheten for at en flaske veier for lite blir 0,007. | |||
[[File: S2_V18_del2_3d.png]] | |||
Ser at forventningsverdien i så fall må være 252,37. | |||
Siste sideversjon per 8. des. 2020 kl. 10:15
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av LektorNilsen
Løsning laget av mattepratbruker Tommy O.
DEL 1
Oppgave 1
a)
b)
c)
Oppgave 2
Legger sammen likning II og III.
Setter inn
Setter inn
Løsning:
Oppgave 3
a)
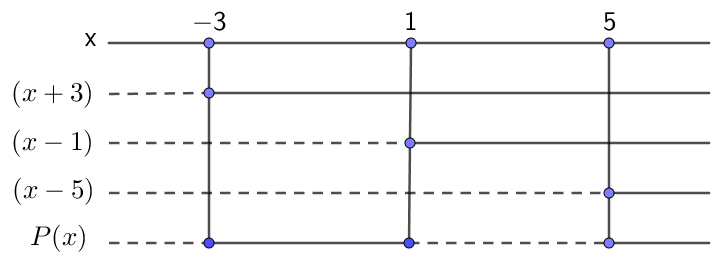
x=1 er et nullpunkt, så P(x) er delelig med (x-1).
b)
Utfører polynomdivisjon for å faktorisere P(x)
Resten faktoriseres:
Vi har
Løsningen kan også skrives som
Oppgave 4
a)
Differansen, d, mellom to ledd i en aritmetisk rekke er konstant. Finner d:
| n | 1 | 2 | 3 | 4 | n |
| 2 | 6 | 10 | 14 | ||
| Formel |
b)
Summen av en aritmetisk rekke er gitt ved:
Finner
Regner ut summen av de 100 første leddene i vår rekke:
Oppgave 5
a)
Dersom
Her har vi
Regner ut summen av rekken når n går mot uendelig:
b)
Dette er en geometrisk rekke hvor
Siden
Det betyr at
Oppgave 6
a)
Bruker kvotientregelen for derivasjon.
Alle potenser av
b)
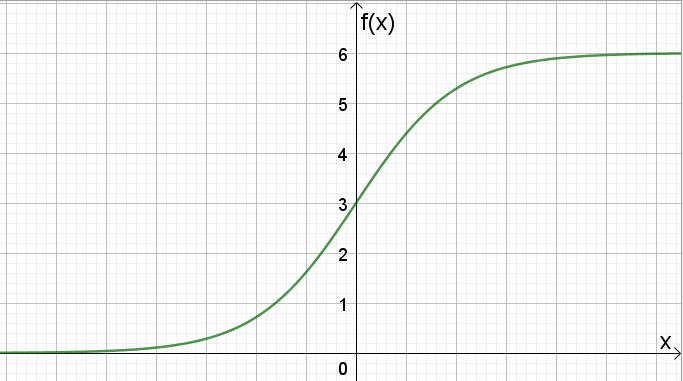
Finner grenseverdien av f(x) når x går mot uendelig:
Det vil si at når x går mot uendelig, går
Finner grenseverdien av f(x) når x går mot minus uendelig:
Det vil si at når x går mot minus uendelig, går
Altså er
c)
Bruker kvotientregelen for derivasjon.
Brøken kan forkortes videre, men vi behøver ikke det. Vi skal finne x-verdien hvor
Vi har
d)
Vi vet at
Oppgave 7
a)
X er binomisk fordelt fordi:
- Vi har et forsøk med delforsøk (10 delforsøk i dette tilfellet)
- Det er to utfall i delforsøkene:
- Delforsøkene er uavhengige av hverandre. Fargen på kulen du trekker i ett delforsøk, påvirker ikke fargen på kulen du trekker i neste delforsøk.
b)
Oppgave 8
a)
Sannsynligheten for at et tilfeldig valgt rugbrød veier mellom 0,90 kg og 1,10 kg er 95,45%.
b)
Sannsynligheten for at veksten av rugbrødene på en tilfeldig pall er mellom 99,5 kg og 100,5 kg er ca. 68,3%.
Oppgave 9
Et toppunkt for
Et bunnpunkt for
DEL 2
Oppgave 1
a)
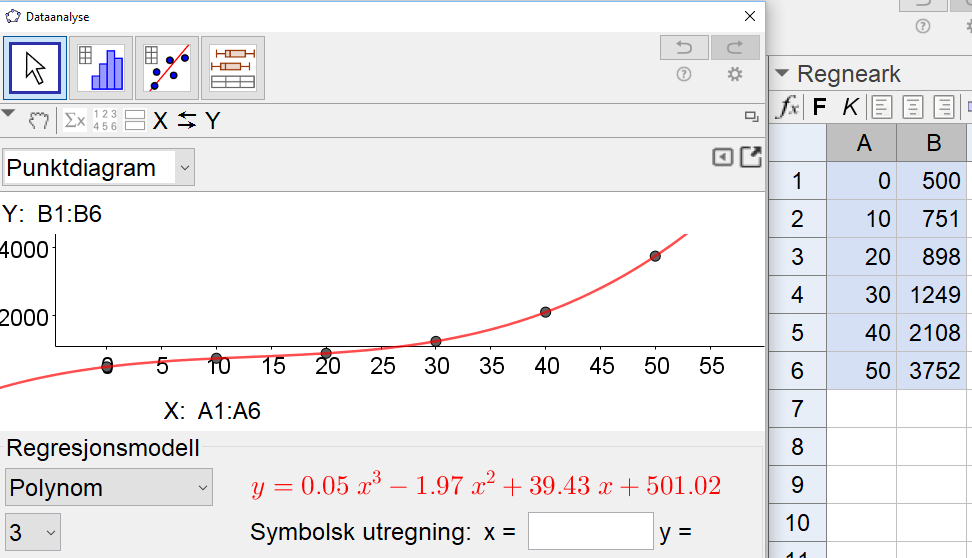
Bruker Geogebra til å utføre en regresjonsanalyse på punktene i tabellen. Velger polynomfunksjon av 3. grad som modell for kostnadene, h(x). Se skjermbildet under.
Jeg har funnet en modell for kostnaden,
Inntekten er 80 kroner per enhet, og kan uttrykkes som
For å finne en modell for overskuddet, O(x), bruker jeg CAS i Geogebra, og regner ut O(x)=I(x)-h(x). Se skjermbildet under.
Jeg har dermed vist at funksjonen
b)
Tegner grafen til O i Geogebra.
c)
Når grensekostnaden er lik grenseinntekten, har vi det største overskuddet. Bruker CAS til å finne den daglige produksjonsmengden som gir størst overskudd (og altså grensekostnad lik grenseinntekt):
Ser av CAS (og grafen tegnet i b) at det er størst overskudd når x=34,57. Det er kun mulig å produsere et heltall antall varer. Sjekker derfor om det er 34 eller 35 antall varer produsert som gir det største overskuddet. Det viser seg at en daglig produksjon på 35 varer gir størst daglig overskudd.
d)
Lager en glider a for prisen per enhet. Definerer inntekten
Oppgave 2
a)
Rekke som viser hvor stort beløp Eirik har på kontoen ett år etter siste innbetaling:
Eirik setter ikke inn noen penger på konto det 16. året. Vi har derfor
Regner ut summen av rekken i CAS i Geogebra:
Eirik har 906299,67 kroner på kontoen ett år etter siste innbetaling.
b)
Beløpet etter 15 år,
fordi vi starter med 906299,67 kroner og får 5% rente hvert år, minus en rekke av utbetalinger med tapt renteinntekt for disse utbetalingene.
Utbetalinger,
Etter 15 år skal kontoen være tom, altså
Løser likningen i CAS på Geogebra:
Årlig utbetaling blir på 83157,13 kroner.
c)
Vi ønsker alltid at startbeløpet med renter, minus utbetalinger med tapte renter, skal bli lik starbeløpet igjen. Slik kan utbetalingene fortsette evig. Bruker CAS i Geogebra for å løse likningen:
Årlig utbetaling blir på 43157,13 kroner.
d)
Bruker nåverdi for å løse denne oppgaven. Summen av nåverdiene i forhold til år 2033 kan skrives som denne rekken:
Bruker CAS i Geogebra til å finne ved hvilket år summen av rekken blir lik antall kroner på konto i 2033.
Kontoen er tom når n=19,16. Husk at n=1 tilsvarer år 2033. Det vil si at kontoen er nesten tom ved uttaket 1.juli 2051 (n=19), og helt tom ved siste uttak 1.juli 2052 (n=20).
Oppgave 3
a)
Bruker sannsynlighetskalkulatoren i Geogebra.
Sannsynligheten for at en tilfeldig flaske veier for lite er 0,0478, altså 4,78%.
b)
Bruker sannsynlighetskalkulatoren i Geogebra.
Sannsynligheten for at en tilfeldig valgt eske skal inneholde én eller flere flasker som veier for lite er 0,5204, dvs 52,04%.
c)
Fortsetter i sannsynlighetskalkulatoren fra oppgave b) og justerer sannsynligheten for at en flaske veier for lite, slik at sannsynligheten for at en tilfeldig valgt eske inneholder én eller flere flasker som veier for lite blir 0,10 (altså 10%).
Ser at sannsynligheten for at en flakse veier for lite i så fall må være 0,007, dvs 0,70%.
d)
Tar opp sannsynlighetskalkulatoren fra oppgave a) og justerer forventningsverdien slik at sannsynligheten for at en flaske veier for lite blir 0,007.
Ser at forventningsverdien i så fall må være 252,37.