2PY 2018 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (69 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
*[https://matematikk.net/matteprat/download/file.php?id=2190 oppgaven som pdf] | |||
*[https://goo.gl/5CpKop Løsningsforslag (pdf)] fra joes. Send gjerne en [mailto:espen.johanssen+matematikknet@gmail.com?subject=Kommentar%20til%202PY%20V18%20fasit melding] hvis du oppdager feil i akkurat dette løsningsforslaget. På forhånd, takk. | *[https://goo.gl/5CpKop Løsningsforslag (pdf)] fra joes. Send gjerne en [mailto:espen.johanssen+matematikknet@gmail.com?subject=Kommentar%20til%202PY%20V18%20fasit melding] hvis du oppdager feil i akkurat dette løsningsforslaget. På forhånd, takk. | ||
*[https://drive.google.com/ | *[https://drive.google.com/file/d/1KfnZbzsnn-y6U-rEcYf-cz_3uqGzYcoe/view?usp=sharing Løsningsforslag eksamen 2PY V18 (pdf)] laget av Jon Bjarne Bø. | ||
* [https://www.matematikk.net/matteprat/download/file.php?id=2138 Løsningsforslag laget av LektorNilsen (pdf)] | |||
=DEL EN= | |||
==Oppgave 1== | ==Oppgave 1== | ||
| Linje 24: | Linje 28: | ||
==Oppgave 4== | ==Oppgave 4== | ||
==a)== | ===a)=== | ||
[[File:1-4a.png]] | [[File:1-4a.png]] | ||
==b)== | ===b)=== | ||
80 personer har fedme. | 80 personer har fedme. | ||
| Linje 38: | Linje 42: | ||
92% av personene er undervektige, normalvektige eller overvektige. | 92% av personene er undervektige, normalvektige eller overvektige. | ||
==c)== | ===c)=== | ||
Medianen er vekten til personen mellom nr. 500 og 501 (siden det er 1000 personer med i undersøkelsen), og vi ser i den kumulative frekvensen at denne personen befinner seg i klassen for normalvektige. | Medianen er vekten til personen mellom nr. 500 og 501 (siden det er 1000 personer med i undersøkelsen), og vi ser i den kumulative frekvensen at denne personen befinner seg i klassen for normalvektige. | ||
| Linje 44: | Linje 48: | ||
==Oppgave 5== | ==Oppgave 5== | ||
==a)== | ===a)=== | ||
[[File:1-5a.png]] | [[File:1-5a.png]] | ||
==b)== | ===b)=== | ||
Antall sirkler i ytterste sekskant er 246. Vi bruker formelen for antall sirkler i ytterste sekstant, og setter den lik 246: | Antall sirkler i ytterste sekskant er 246. Vi bruker formelen for antall sirkler i ytterste sekstant, og setter den lik 246: | ||
| Linje 58: | Linje 62: | ||
Dermed vet vi at det er 41 sekskanter i figuren. | Dermed vet vi at det er 41 sekskanter i figuren. | ||
==c)== | ===c)=== | ||
[[File:1-5b.png]] | [[File:1-5b.png]] | ||
==d)== | ===d)=== | ||
Bruker formelen for antall sirkler i figuren og setter | Bruker formelen for antall sirkler i figuren og setter inn n=100. | ||
$2 \cdot n^2 - n \\ = 2 \cdot 100^2 -100 \\ = 2 \cdot 10000 - 100 \\ = 20000 - 100 \\ = 19900$ | $2 \cdot n^2 - n \\ = 2 \cdot 100^2 -100 \\ = 2 \cdot 10000 - 100 \\ = 20000 - 100 \\ = 19900$ | ||
| Linje 72: | Linje 76: | ||
==Oppgave 6== | ==Oppgave 6== | ||
==a)== | ===a)=== | ||
En lineær modell skrives $y=a \cdot x + b$ | En lineær modell skrives $y=a \cdot x + b$ | ||
| Linje 80: | Linje 84: | ||
Vi finner stigningstallet $a = \frac{y_2-y_1}{x_2-x_1} = \frac{6000-12000}{10-0} = \frac{-6000}{10} = -600$ | Vi finner stigningstallet $a = \frac{y_2-y_1}{x_2-x_1} = \frac{6000-12000}{10-0} = \frac{-6000}{10} = -600$ | ||
Modellen som viser hvor mange dyr det vil være i bestanden om x år er $y=-600x+12000$ | Modellen som viser hvor mange dyr det vil være i bestanden om ''x'' år er $y=-600x+12000$ | ||
==b)== | ===b)=== | ||
$\frac{11400}{12000}=0,95$ | $\frac{11400}{12000}=0,95$ | ||
| Linje 90: | Linje 94: | ||
Den eksponentielle modellen som viser hvor mange dyr det vil være i bestanden om x år er $f(x)=12000 \cdot 0,95^x$ | Den eksponentielle modellen som viser hvor mange dyr det vil være i bestanden om x år er $f(x)=12000 \cdot 0,95^x$ | ||
==c)== | ===c)=== | ||
I den lineære modellen avtar bestanden med 600 dyr hvert år. Det første året tilsvarer det 5% av startverdien på 12 000 dyr. Bestanden vil fortsette å avta med 600 dyr hvert år, og det vil tilsvare en større og større prosentandel av dyrene som er igjen hvert år. | I den lineære modellen avtar bestanden med 600 dyr hvert år. Det første året tilsvarer det 5% av startverdien på 12 000 dyr. Bestanden vil fortsette å avta med 600 dyr hvert år, og det vil tilsvare en større og større prosentandel av dyrene som er igjen hvert år. | ||
| Linje 97: | Linje 101: | ||
Det vil si at det vil være færrest dyr igjen om 10 år ifølge den lineære modellen. | Det vil si at det vil være færrest dyr igjen om 10 år ifølge den lineære modellen. | ||
==DEL TO== | |||
==Oppgave 1== | |||
===a)=== | |||
[[File: 1a.png]] | |||
Tegner funksjonen i Geogebra. | |||
===b)=== | |||
[[File: 1b.png]] | |||
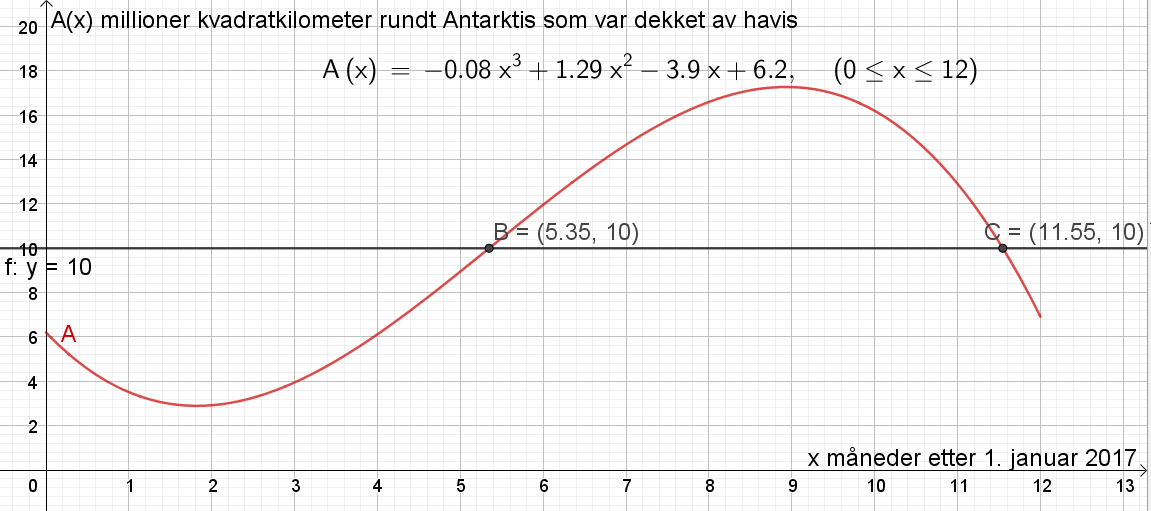
Tegner linja y=10 og bruker ''Skjæring mellom to objekt'' for å finne punkt B=(5,35, 10) og C=(11,55, 10), se figur. | |||
5,35 måneder etter 1. januar tilsvarer litt ut i juni måned. 11,55 måneder etter 1. januar tilsvarer midten av desember (husk at x=0 den 1.januar, x=1 den 1. februar osv.). Det vil si at det varte i 11,55-5,35=6,2 måneder. | |||
Det var mer enn 10 millioner kvadratkilometer dekket av havis fra litt ut i juni til midten av desember, i 6,2 måneder. | |||
===c)=== | |||
[[File: 1c.png]] | |||
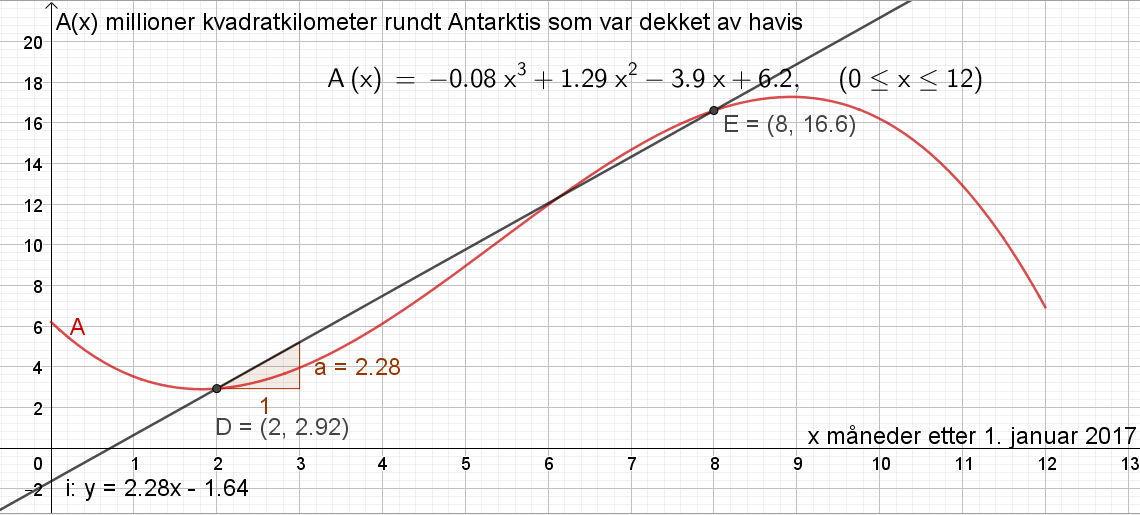
1. mars tilsvarer x=2 (2 måneder etter 1. januar). 1. september tilsvarer x= 8 (8 måneder etter 1. januar). | |||
Tegnet punktene D=(2,A(2)) og E=(8,A(8)). Brukte knappen "linje" til å tegne en linje ''i'' som går gjennom punkt D og E. Brukte knappen "Stigning" til å finne stigningen til linjen ''i''. Stigningen a=2,28. | |||
Det betyr at den gjennomsnittlige økningen i antall kvadratkilometer dekket av havvis fra 1. mars til 1. september var 2,28 millioner kvadratkilometer per måned. | |||
===d)=== | |||
[[File: 1d.png]] | |||
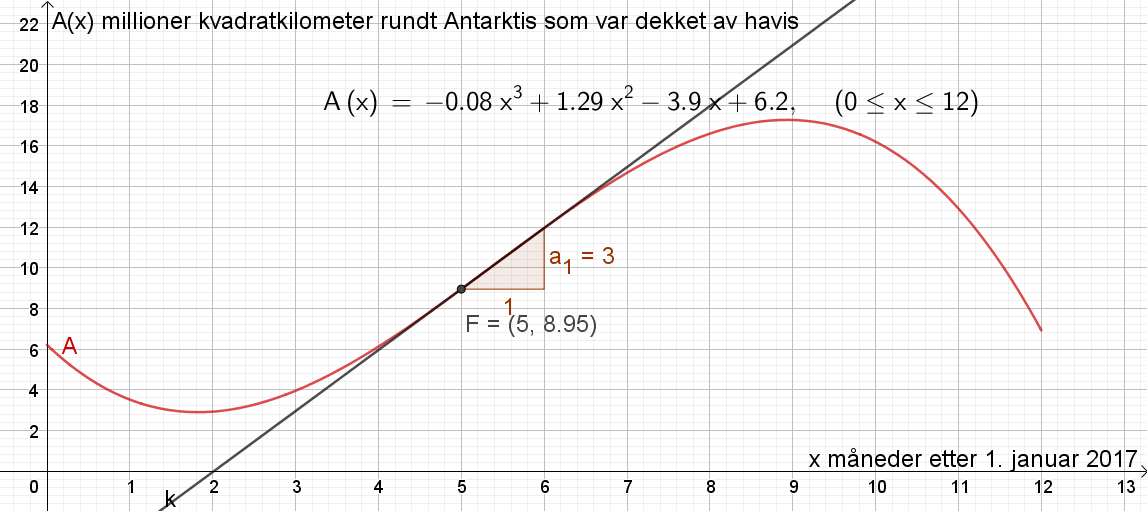
Lagde punktet F=(5,A(5)). Brukte knappen "Tangent" til å lage en tangent til funksjonen A(x) i punktet F. Brukte knappen "Stigning" til å finne stigningen til tangenten. Stigningen a=3. | |||
Den momentane vekstfarten når x=5 var 3 millioner kvadratkilometer per måned. Det vil si at havisen vokste med en fart på 3 millioner kvadratkilometer per måned den 1. juni. | |||
==Oppgave 2== | |||
===a)=== | |||
Setter om et funksjonsuttrykk ''f(x)'' for verdien av bilen om ''x'' år. En årlig nedgang i verdien på 12% tilsvarer en årlig vekstfaktor på 0,88. | |||
$f(x)=300000 \cdot 0,88^x$ | |||
Om 5 år er bilen verdt: | |||
$f(5)=300000 \cdot 0,88^5 \approx 158320 kr$ | |||
===b)=== | |||
For 5 år siden var bilen verdt: | |||
$f(-5)=300000 \cdot 0,88^{-5} \approx 568470 kr$ | |||
==Oppgave 3== | |||
===a)=== | |||
For å finne antall personer i boligområdet finner vi frekvensen i hver aldersgruppe (klassebredden ganget med histogramhøyden), og legger sammen frekvensen i alle aldersgruppene. | |||
$15 \cdot 3 + 5 \cdot 5 + 10 \cdot 7 + 20 \cdot 5 + 30 \cdot 1 = 270$ | |||
Det bor 270 personer i boligområdet. | |||
===b)=== | |||
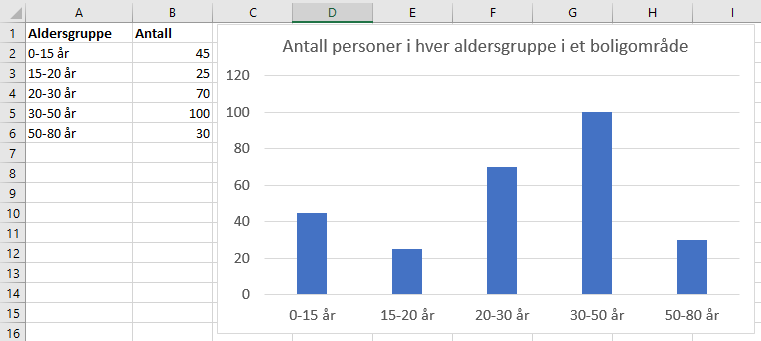
Bruker Excel til å lage et søylediagram. | |||
[[File: 3b.png]] | |||
===c)=== | |||
I et søylediagram er det lettere å se antall personer i hver aldersgruppe. Mange vil kanskje foretrekke søylediagram, da antall personer i hver aldersgruppe blir lett å sammenligne. | |||
I et histogram er det lettere å se bredden på de ulike aldersgruppene. | |||
Valg av diagram kommer altså an på hvilken informasjon man vil legge vekt på. | |||
==Oppgave 4== | |||
===a)=== | |||
[[File: 2-4a.png]] | |||
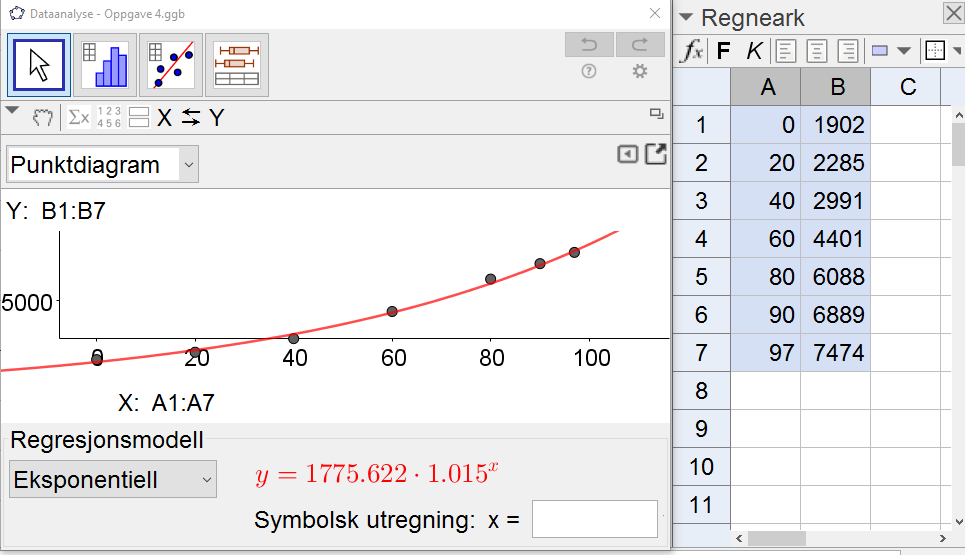
Legger inn verdiene i regnearket i Geogebra og bruker ''Regresjonsanalyse'' for å finne en eksponentiell modell. Husk at x=0 i 1920, x=20 i 1940 osv. | |||
Vi har vist at modellen $f(x)=1775,6 \cdot 1,015^x$ passer fint med tallene i tabellen. | |||
===b)=== | |||
Vekstfaktoren i modellen er 1,015, det betyr at folketall øker med 1,5% per år ifølge modellen. | |||
===c)=== | |||
[[File: 4c.png]] | |||
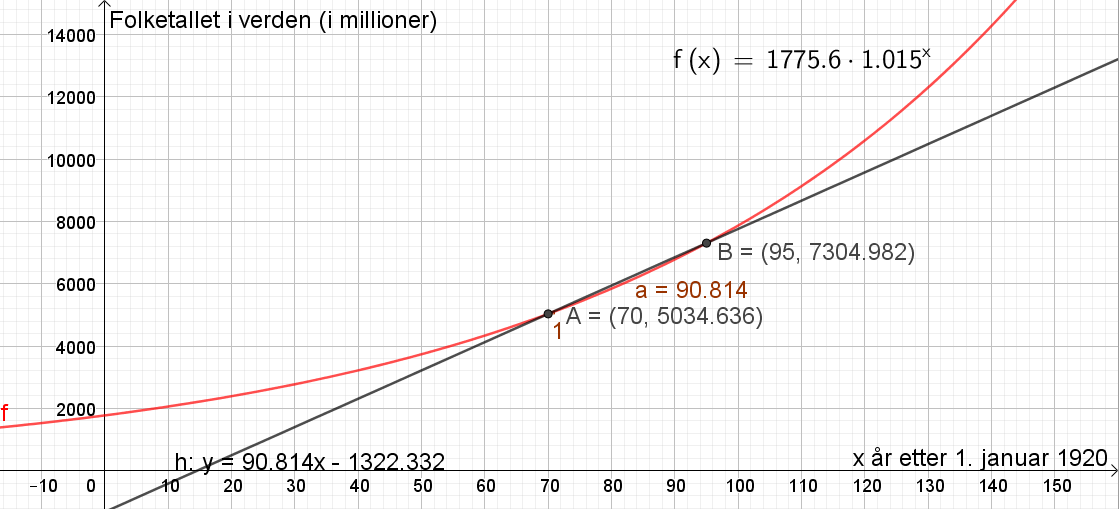
Tegner funksjonen f(x) i Geogebra. Lager punktene A=(70,f(70)) og B=(95, f(95)). Bruker knappen ''Linje'' til å lage linja ''h'' som går gjennom punkt A og B. Bruker knappen ''Stigning'' til å finne stigninga til linjen ''h''. Stigningen a=90,8. | |||
Det vil si at folketallet steg med gjennomsnittlig 90,8 millioner per år fra 1990 til 2015. | |||
===d)=== | |||
[[File: 4d.png]] | |||
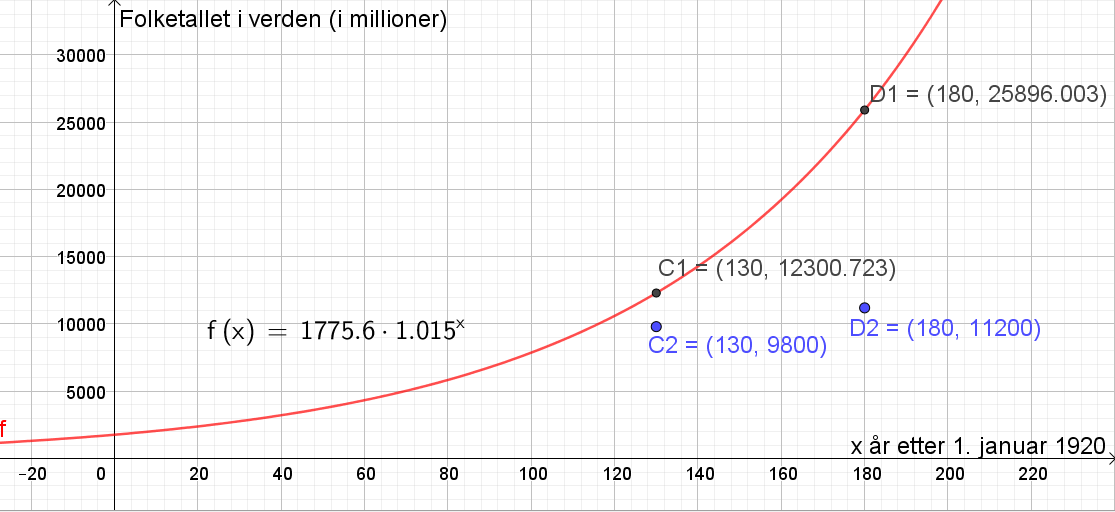
År 2050 tilsvarer x=130. Et folketall på 9,8 milliarder tilsvarer y= 9800. År 2100 tilsvarer x=180. Et folketall på 11,2 milliarder tilsvarer y= 11200. | |||
Lager punktet C1=(130, (f(130)) og C2=(130, 9800). Vi ser at modellen ikke stemmer helt med FNs prognoser for år 2050. Vår modell forutsier 12,3 milliarder mennesker i 2050, som er et noe høyere folketall enn FNs prognoser på 9,8 milliarder. | |||
Lager punktet D1=(180, (f(180)) og D2=(180, 11200). Vi ser at modellen ikke stemmer i det hele tatt med FNs prognoser for år 2100. Vår modell forutsier 25,9 milliarder mennesker i 2100, som er over dobbelt så høyt folketall som FNs prognoser på 11,2 milliarder. | |||
==Oppgave 5== | |||
===a)=== | |||
$\frac{5+20+40}{5+20+40+65+55+15} = \frac{65}{200} = 0,352 = 32,5$% | |||
32,5% av elevene fikk karakter 4 eller bedre. | |||
===b)=== | |||
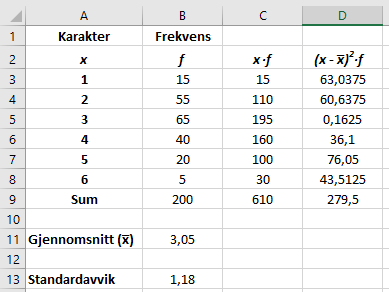
Bruker Excel. | |||
[[File: 5b.png]] | |||
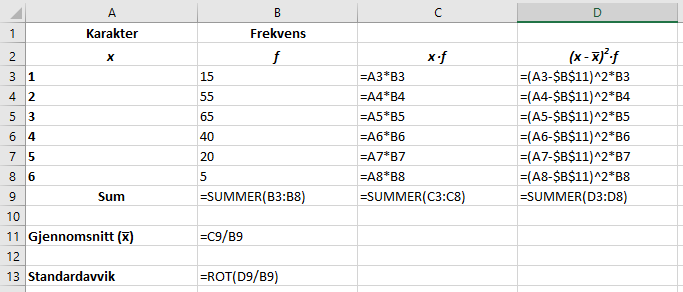
Med formler: | |||
[[File: 5b2.png]] | |||
===c)=== | |||
For hvert av de to årene ganger vi gjennomsnittet med frekvensen for å få summen av karakterene: | |||
År 1: $3,05 \cdot 200 = 610$ | |||
År 2: $3,25 \cdot 180 = 585$ | |||
For å finne det nye gjennomsnittet legger vi sammen summen av karakterene og deler på summen av antall elever: | |||
Gjennomsnitt for begge årene = $\frac{610+585}{200+180} = 3,145$ | |||
==Oppgave 6== | |||
===a)=== | |||
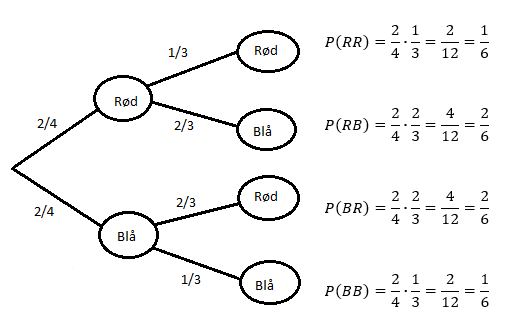
[[File: 6a.png]] | |||
P(to kuler med samme farge) = $\frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$ | |||
P(to kuler med ulik farge) = $\frac{2}{6} + \frac{2}{6} = \frac{4}{6} = \frac{2}{3}$ | |||
Påstand 2 er riktig, det er mest sannsynlig at hun kommer til å trekke to kuler med ulik farge. | |||
===b)=== | |||
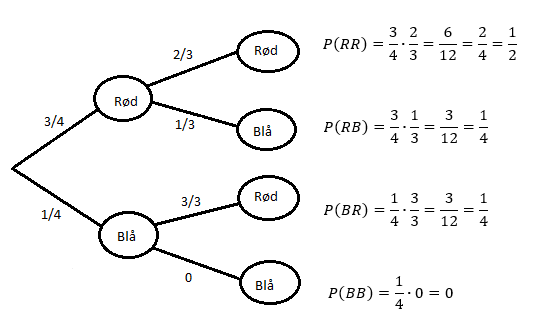
[[File: 6b.png]] | |||
P(to kuler med samme farge) = $\frac{1}{2}$ | |||
P(to kuler med ulik farge) = $\frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$ | |||
Påstand 3 er riktig, sannsynligheten for at hun kommer til å trekke to kuler med samme farge, er like stor som sannsynligheten for at hun kommer til å trekke to kuler med ulik farge. | |||
Siste sideversjon per 10. jan. 2019 kl. 10:19
- Løsningsforslag (pdf) fra joes. Send gjerne en melding hvis du oppdager feil i akkurat dette løsningsforslaget. På forhånd, takk.
- Løsningsforslag eksamen 2PY V18 (pdf) laget av Jon Bjarne Bø.
DEL EN
Oppgave 1
Variasjonsbredde: $30-(-24) = 30 + 24 = 54$ poeng
Gjennomsnitt: $\frac{20-15+5+15-8-3-24+30}{8} = \frac{20}{8} = \frac{5}{2} = 2,5 $ poeng
Oppgave 2
$\frac{20}{100} \cdot 25 = \frac{500}{100} = 5 $
5 elever i klassen til Mats har bodd i Norge i mindre enn fire år.
Oppgave 3
$\frac{5 \cdot 10^6}{2 \cdot 10^{-8}} = \frac{5}{2} \cdot 10^{6-(-8)} = 2,5 \cdot 10^{14} $
Oppgave 4
a)
b)
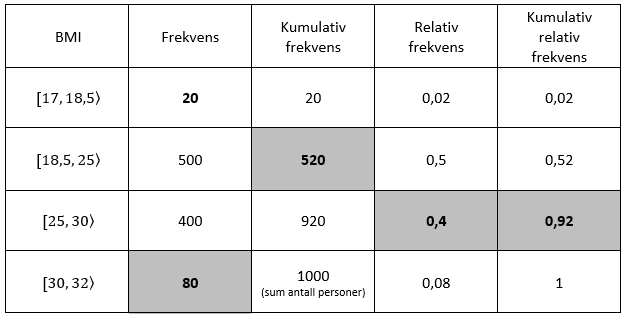
80 personer har fedme.
520 personer er undervektige eller normalvektige.
40% av personene er overvektige.
92% av personene er undervektige, normalvektige eller overvektige.
c)
Medianen er vekten til personen mellom nr. 500 og 501 (siden det er 1000 personer med i undersøkelsen), og vi ser i den kumulative frekvensen at denne personen befinner seg i klassen for normalvektige.
Oppgave 5
a)
b)
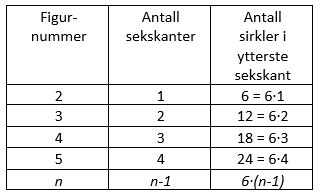
Antall sirkler i ytterste sekskant er 246. Vi bruker formelen for antall sirkler i ytterste sekstant, og setter den lik 246:
$6 \cdot (n-1) = 246 \\ n-1 = \frac{246}{6} \\ n-1 = 41 $
Formel for antall sekskanter i en figur er $n-1$
Dermed vet vi at det er 41 sekskanter i figuren.
c)
d)
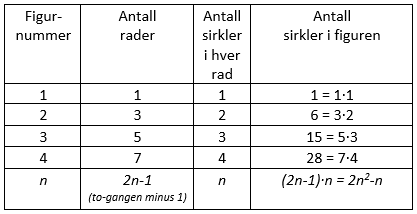
Bruker formelen for antall sirkler i figuren og setter inn n=100.
$2 \cdot n^2 - n \\ = 2 \cdot 100^2 -100 \\ = 2 \cdot 10000 - 100 \\ = 20000 - 100 \\ = 19900$
Det vil være 19 900 sirkler i figur nr. 100.
Oppgave 6
a)
En lineær modell skrives $y=a \cdot x + b$
Vi vet at konstantleddet b = 12 000 fordi dyrebestanden i dag er 12 000 dyr.
Vi finner stigningstallet $a = \frac{y_2-y_1}{x_2-x_1} = \frac{6000-12000}{10-0} = \frac{-6000}{10} = -600$
Modellen som viser hvor mange dyr det vil være i bestanden om x år er $y=-600x+12000$
b)
$\frac{11400}{12000}=0,95$
11 400 dyr tilsvarer 95% av 12 000 dyr. Det betyr at vekstfaktoren for ett år er 0,95.
Den eksponentielle modellen som viser hvor mange dyr det vil være i bestanden om x år er $f(x)=12000 \cdot 0,95^x$
c)
I den lineære modellen avtar bestanden med 600 dyr hvert år. Det første året tilsvarer det 5% av startverdien på 12 000 dyr. Bestanden vil fortsette å avta med 600 dyr hvert år, og det vil tilsvare en større og større prosentandel av dyrene som er igjen hvert år.
I den eksponentielle modellen avtar bestanden med 5% av antall dyr som er igjen hvert år. Det første året tilsvarer det 600 dyr, men de neste årene vil bestanden minke med færre og færre dyr, fordi 5% av en stadig minkende bestand, tilsvarer et mindre og mindre antall dyr.
Det vil si at det vil være færrest dyr igjen om 10 år ifølge den lineære modellen.
DEL TO
Oppgave 1
a)
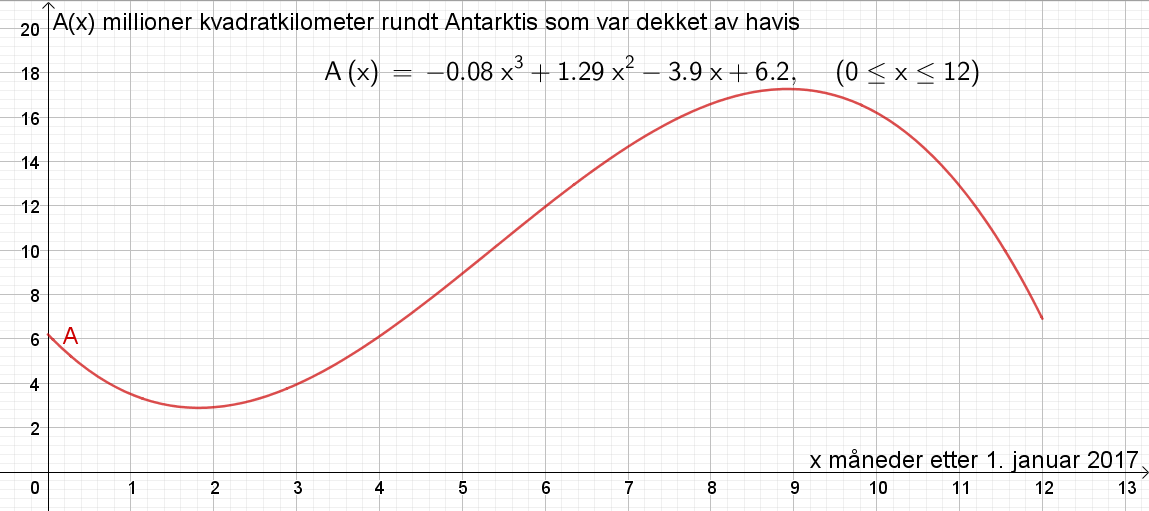
Tegner funksjonen i Geogebra.
b)
Tegner linja y=10 og bruker Skjæring mellom to objekt for å finne punkt B=(5,35, 10) og C=(11,55, 10), se figur.
5,35 måneder etter 1. januar tilsvarer litt ut i juni måned. 11,55 måneder etter 1. januar tilsvarer midten av desember (husk at x=0 den 1.januar, x=1 den 1. februar osv.). Det vil si at det varte i 11,55-5,35=6,2 måneder.
Det var mer enn 10 millioner kvadratkilometer dekket av havis fra litt ut i juni til midten av desember, i 6,2 måneder.
c)
1. mars tilsvarer x=2 (2 måneder etter 1. januar). 1. september tilsvarer x= 8 (8 måneder etter 1. januar).
Tegnet punktene D=(2,A(2)) og E=(8,A(8)). Brukte knappen "linje" til å tegne en linje i som går gjennom punkt D og E. Brukte knappen "Stigning" til å finne stigningen til linjen i. Stigningen a=2,28.
Det betyr at den gjennomsnittlige økningen i antall kvadratkilometer dekket av havvis fra 1. mars til 1. september var 2,28 millioner kvadratkilometer per måned.
d)
Lagde punktet F=(5,A(5)). Brukte knappen "Tangent" til å lage en tangent til funksjonen A(x) i punktet F. Brukte knappen "Stigning" til å finne stigningen til tangenten. Stigningen a=3.
Den momentane vekstfarten når x=5 var 3 millioner kvadratkilometer per måned. Det vil si at havisen vokste med en fart på 3 millioner kvadratkilometer per måned den 1. juni.
Oppgave 2
a)
Setter om et funksjonsuttrykk f(x) for verdien av bilen om x år. En årlig nedgang i verdien på 12% tilsvarer en årlig vekstfaktor på 0,88.
$f(x)=300000 \cdot 0,88^x$
Om 5 år er bilen verdt:
$f(5)=300000 \cdot 0,88^5 \approx 158320 kr$
b)
For 5 år siden var bilen verdt:
$f(-5)=300000 \cdot 0,88^{-5} \approx 568470 kr$
Oppgave 3
a)
For å finne antall personer i boligområdet finner vi frekvensen i hver aldersgruppe (klassebredden ganget med histogramhøyden), og legger sammen frekvensen i alle aldersgruppene.
$15 \cdot 3 + 5 \cdot 5 + 10 \cdot 7 + 20 \cdot 5 + 30 \cdot 1 = 270$
Det bor 270 personer i boligområdet.
b)
Bruker Excel til å lage et søylediagram.
c)
I et søylediagram er det lettere å se antall personer i hver aldersgruppe. Mange vil kanskje foretrekke søylediagram, da antall personer i hver aldersgruppe blir lett å sammenligne.
I et histogram er det lettere å se bredden på de ulike aldersgruppene.
Valg av diagram kommer altså an på hvilken informasjon man vil legge vekt på.
Oppgave 4
a)
Legger inn verdiene i regnearket i Geogebra og bruker Regresjonsanalyse for å finne en eksponentiell modell. Husk at x=0 i 1920, x=20 i 1940 osv.
Vi har vist at modellen $f(x)=1775,6 \cdot 1,015^x$ passer fint med tallene i tabellen.
b)
Vekstfaktoren i modellen er 1,015, det betyr at folketall øker med 1,5% per år ifølge modellen.
c)
Tegner funksjonen f(x) i Geogebra. Lager punktene A=(70,f(70)) og B=(95, f(95)). Bruker knappen Linje til å lage linja h som går gjennom punkt A og B. Bruker knappen Stigning til å finne stigninga til linjen h. Stigningen a=90,8.
Det vil si at folketallet steg med gjennomsnittlig 90,8 millioner per år fra 1990 til 2015.
d)
År 2050 tilsvarer x=130. Et folketall på 9,8 milliarder tilsvarer y= 9800. År 2100 tilsvarer x=180. Et folketall på 11,2 milliarder tilsvarer y= 11200.
Lager punktet C1=(130, (f(130)) og C2=(130, 9800). Vi ser at modellen ikke stemmer helt med FNs prognoser for år 2050. Vår modell forutsier 12,3 milliarder mennesker i 2050, som er et noe høyere folketall enn FNs prognoser på 9,8 milliarder.
Lager punktet D1=(180, (f(180)) og D2=(180, 11200). Vi ser at modellen ikke stemmer i det hele tatt med FNs prognoser for år 2100. Vår modell forutsier 25,9 milliarder mennesker i 2100, som er over dobbelt så høyt folketall som FNs prognoser på 11,2 milliarder.
Oppgave 5
a)
$\frac{5+20+40}{5+20+40+65+55+15} = \frac{65}{200} = 0,352 = 32,5$%
32,5% av elevene fikk karakter 4 eller bedre.
b)
Bruker Excel.
Med formler:
c)
For hvert av de to årene ganger vi gjennomsnittet med frekvensen for å få summen av karakterene:
År 1: $3,05 \cdot 200 = 610$
År 2: $3,25 \cdot 180 = 585$
For å finne det nye gjennomsnittet legger vi sammen summen av karakterene og deler på summen av antall elever:
Gjennomsnitt for begge årene = $\frac{610+585}{200+180} = 3,145$
Oppgave 6
a)
P(to kuler med samme farge) = $\frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$
P(to kuler med ulik farge) = $\frac{2}{6} + \frac{2}{6} = \frac{4}{6} = \frac{2}{3}$
Påstand 2 er riktig, det er mest sannsynlig at hun kommer til å trekke to kuler med ulik farge.
b)
P(to kuler med samme farge) = $\frac{1}{2}$
P(to kuler med ulik farge) = $\frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}$
Påstand 3 er riktig, sannsynligheten for at hun kommer til å trekke to kuler med samme farge, er like stor som sannsynligheten for at hun kommer til å trekke to kuler med ulik farge.