R1 2016 høst LØSNING: Forskjell mellom sideversjoner
mIngen redigeringsforklaring |
|||
| (87 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/download/file.php?id=1333 Løsning laget av | [http://www.matematikk.net/matteprat/download/file.php?id=1333 Løsning laget av Dennis Christensen] | ||
[http://matematikk.net/matteprat/viewtopic.php?f=13&t=44289 Diskusjon av og delvis løsning på denne oppgaven] | [http://matematikk.net/matteprat/viewtopic.php?f=13&t=44289 Diskusjon av og delvis løsning på denne oppgaven] | ||
| Linje 20: | Linje 20: | ||
===c)=== | ===c)=== | ||
$h(x)=\frac {e^{2x}}{x-3} \\ h'(x)= \frac{2e^{2x} (x-3)- e^{2x}}{(x-3)^2} = \frac{(2x | $h(x)=\frac {e^{2x}}{x-3} \\ h'(x)= \frac{2e^{2x} (x-3)- e^{2x}}{(x-3)^2} = \frac{(2x-7)e^{2x}}{(x-3)^2}$ | ||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | ===a)=== | ||
$f(x)=0 \\ (x+1)^2(x-2) \\ x=-1 \vee x=2$ | |||
Nullpunkter: (-1, 0) og (2, 0) | |||
===b)=== | ===b)=== | ||
$f'(x)=0 \\ f'(x) = 2(x+1)(x-2) + (x+1)^2 = (x+1)(3x-3) \\ x =-1 \vee x= 1$ | |||
f'(-2) > 0, f'(0) < 0 og f'(2) > 0 gir toppunkt i ( -1, 0) og minimum for (1,-4 ). | |||
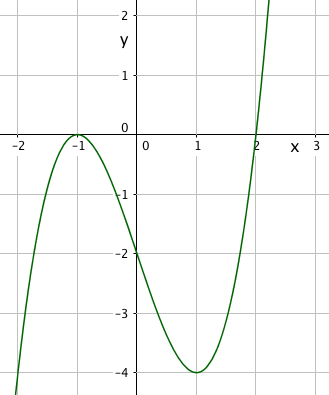
===c)=== | ===c)=== | ||
[[File:r1-h2016-1-2c.png]] | |||
==Oppgave 3== | ==Oppgave 3== | ||
| Linje 36: | Linje 45: | ||
===a)=== | ===a)=== | ||
$\frac{2x + 10}{x^2-25} +\frac{x}{x+5} - \frac {4}{2x - 10}= \\\frac{2x + 10}{(x+5)(x-5)} +\frac{x}{x+5} - \frac {4}{2(x-5)}= \\ \frac{4x+20+2x(x-5) - 4(x+5)}{2(x+5)(x-5) } = \\ \frac{2x(x-5)}{2(x+5)(x-5)} = \\ \frac{x}{x+5}$ | |||
===b)=== | ===b)=== | ||
$\frac{2x+10}{x^2-25} + \frac{x}{x+5} = \frac{4}{2x-10} \\ 2(2x+10) + 2x(x-5) = 4(x+5) \\ 4x+20+2x^2-10x = 4x + 20 \\2x^2-10x=0 \\ x=0 \vee 2x-10=0 \\ x= 0 \vee x= 5$ | |||
Må forkaste x = 5, da det gir null i nevner. | |||
L={ 0 } | |||
En mere elegant og tidsbesparende løsning er å løse svaret fra a lik null: | |||
$\frac {x}{x+5} =0$ | |||
som gir x=0 direkte. | |||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 44: | Linje 66: | ||
===a)=== | ===a)=== | ||
$2^{3x-2} - 13 = 3 \\ 2^{3x-2} = 2^4 \\ 3x-2 = 4 \\ 3x=6 \\ x= | $2^{3x-2} - 13 = 3 \\ 2^{3x-2} = 2^4 \\ 3x-2 = 4 \\ 3x=6 \\ x=2$ | ||
===b)=== | ===b)=== | ||
$ (lgx)^2 +lgx-2=0 \\ u=lgx\\ u^2+u-2 =0 \\ ABC- formel \\ u= -2 \vee u = 1 \\ $ | $ (lgx)^2 +lgx-2=0 \\ u=lgx\\ u^2+u-2 =0 \\ ABC- formel \\ u= -2 \vee u = 1 \\ lgx = -2 \vee lgx =1 \\ x=0,01 \vee x= 10$ | ||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
[ 1, 1] er parallell med AB vektor: | |||
<math> \left[ \begin{align*}x = -4 + t\\ y = 5+ t \end{align*}\right] </math> | |||
===b)=== | |||
Skjærer x - aksen betyr at y = 0. Da må t være - 5. | |||
Da blir x = -9 | |||
D ( -9, 0) | |||
===c)=== | |||
$[1, 1] \cdot [-3+4-t, -2-5-t] =0 \\ 1 -t - 7 - t =0 \\ t=-3 \\ x= -7 \wedge y=2$ | |||
E ( -7, 2) | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
$P(D|A)= 0,04 \\ P(D|B)= 0,01 \\ P(A) = \frac 13 \\ P(B)= \frac 23$ | |||
Total sannsynlighet for defekt nøkkel | |||
$P(D)= P(A) \cdot P(D|A) + P(B) \cdot P(D|B) \\ P(D)= \frac 13 \cdot 0,04 + \frac 23 \cdot 0,01 = 0,06 :3 = 0,02 $ | |||
Det er 2% sannsynlig at nøkkelen er defekt. | |||
===b)=== | |||
$P(D) \cdot P(A|D) = P(A) \cdot P(D|A) \\ P(A|D)= \frac{P(A) \cdot P(D|A)}{P(D)} = \frac 13 \cdot \frac {0,04}{0,02} = \frac 23$ | |||
Det er ca. 67% sannsynlig at en defekt nøkkel kommer fra maskin A. | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | ===a)=== | ||
$ \triangle PCB$ er likebeint, derfor er $\angle PCB = v $ | |||
$\angle PCE$ er 90 grader fordi toppunktet ligger på periferien og den spenner over 180 grader av sirkelsektoren. | |||
$ \angle ABC$ er også 90 grader, derfor må $\angle ACE = v. $ | |||
$ \angle A$ er felles i begge trekantene og $\angle ACE = \angle PCB = v$, derfor er trekantene formlike. | |||
===b)=== | ===b)=== | ||
| Linje 66: | Linje 136: | ||
===c)=== | ===c)=== | ||
Forholdet mellom | Forholdet mellom samsvarende sider i formlike trekanter er likt. | ||
$\frac{AP}{AC} = \frac{AC}{AE} \\ \frac{c+a}{b} = \frac{b}{c-a}$ | $\frac{AP}{AC} = \frac{AC}{AE} \\ \frac{c+a}{b} = \frac{b}{c-a}$ | ||
| Linje 78: | Linje 148: | ||
(ii) er grafen til funksjonen. Den har minimumspunkt for x=0 og vender sin hule side opp hele tiden, dvs. ingen vendepunkter. | (ii) er grafen til funksjonen. Den har minimumspunkt for x=0 og vender sin hule side opp hele tiden, dvs. ingen vendepunkter. | ||
(i) er grafen til f'(x). Den er null | (i) er grafen til f'(x). Den er null origo når f(x) har et minimum. (iii) er grafen til den dobbeltderiverte. | ||
==DEL TO== | ==DEL TO== | ||
==Oppgave 1== | |||
===a)=== | |||
${34\choose7} = _{34}C_7 = 5 379 616 $ | |||
===b)=== | |||
Hypergeometrisk situasjon: | |||
P (nøyaktig fem rette) $ = \frac{{7\choose5}\cdot {27 \choose 2}}{ {34\choose7} } \approx 0,0014$ , eller 0,14% sannsynlig. | |||
===c)=== | |||
Sannsynligheten for at de tre siste tallene går inn er: | |||
$ = \frac{{3\choose3}\cdot {27 \choose 0}}{ {30\choose3} } \approx 0,0002$ , eller 0,02%. | |||
==Oppgave 2== | |||
===a)=== | |||
Sirkel $C_1 \quad \quad $ Sentrum: $S_1( -5, 0) \quad $ , Radius: $r_1 = \sqrt{80} = 4 \sqrt 5$ | |||
Sirkel $C_2 \quad \quad $ $ \quad x^2-10x+y^2+5=0 \\ x^2 - 10x + 5^2 + y^2 + 5 = 5^2 \\ (x-5)^2+y^2 =20 \\ \\ Sentrum: \quad S_2 (5, 0) \quad \quad Radius: \quad r_2 = \sqrt{20} = 2 \sqrt 5$ | |||
===b)=== | |||
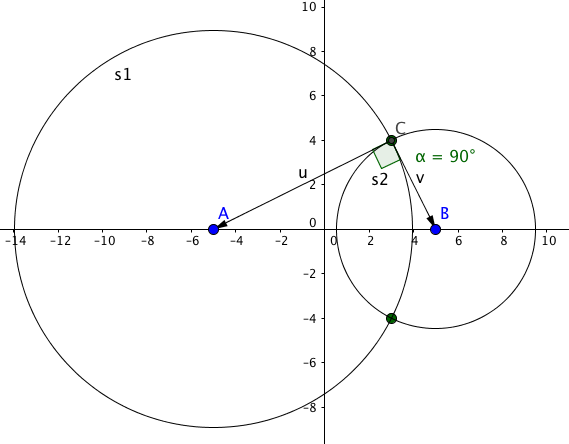
[[File:r1-h2016-2-2b1.png]][[File:r1-h2016-2-2b2.png]] | |||
Skjæringspunktene er ( 3, 4 ) og ( 3, -4 ). | |||
===c)=== | |||
Dersom ortogonale er skalarproduktet mellom vektorene null. | |||
$ \vec{AC} \cdot \vec{CB} = 0 \\ [8,4] \cdot [2, -4] = 16 + ( -16)= 0 $ | |||
Sirklene er ortogonale. | |||
==Oppgave 3== | |||
===a)=== | |||
Fra ungdomsskolen: $ s = vt \\ t = \frac sv $ | |||
x er lengden langs veien og 5 er farten langs veien. Tidsforbruk langs vei: $t_v(x)= \frac x5$ Rotuttrykket i andre ledd er lengden av hypotenusen BH (altså lengden hun beveger seg i terrenget), uttrykt ved katetene i den rettvinklede trekanten BCH. 3 er farten i terrenget. Derav uttrykket. | |||
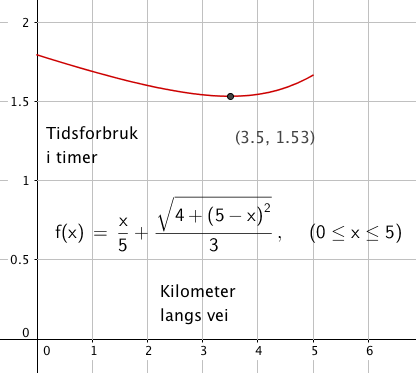
===b)=== | |||
[[File:r1-h2016-2-3b.png]] | |||
Vi ser at hun bruker kortest tid om hun skjærer av vegen etter 3,5 km. Hun bruker da 1,53 timer, eller 1 time 31 minutter og 48 sekunder, for å være nøyaktig. | |||
==Oppgave 4== | |||
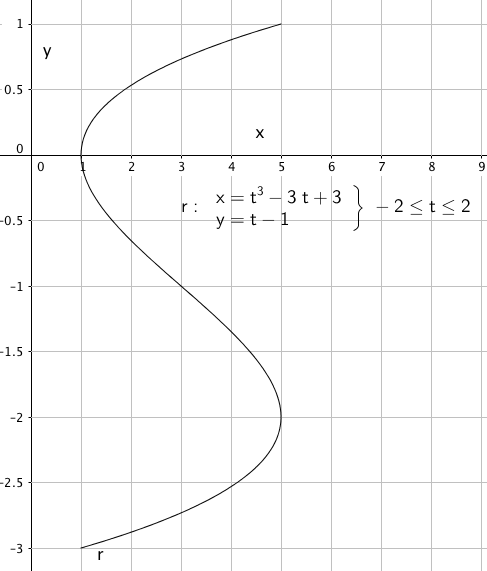
===a)=== | |||
[[File:r1-h2016-2-4a.png]] | |||
===b)=== | |||
$ \vec r(t)= [t^3-3t+3, t-1] \quad \quad -2 \leq x \leq 2 \\ \vec v(t) = \vec r ' (t)= [3t^2-3,1] \\ \vec a(t)= \vec r ' ' (t) = [6t, 0] $ | |||
Når t =1 | |||
$ Posisjon:\quad \vec r(1)= [1^3-3 \cdot 1+3, 1-1] = [1,0] \\ Banefart: | \vec v(1)| = [3 \cdot 1^2-3,1] = |[0,1]| = 1 \\ Akselerasjon:| \vec a(1)|= =| [6 \cdot 1, 0]| =6 $ | |||
Når t = 1 er posisjonen (1,0), banefarten lik 1 og akselerasjonen lik 6. | |||
===c)=== | |||
Fartsvektor parallell med y aksen: | |||
$ \vec v(t) || [0, 1] \\ [3t^2-3] = k[0, 1] \\ 3t^2 - 3 =0 \\ t^2 =1 \\ t = \pm 1$ | |||
Setter t verdiene inn i posisjonsvektoren: | |||
t = 1 har vi fra b : [1,0] | |||
t = -1 gir oss $[-1 +3+3, -2 ] = [5, -2]$ | |||
==Oppgave 5== | |||
[[File:r1-h2016-2-5.png]] | |||
Skjæring mellom parabel og sirkel (sentrum i origo og radius fem) gir de fire punktene vist over. | |||
Siste sideversjon per 26. nov. 2017 kl. 16:56
Løsning laget av Dennis Christensen
Diskusjon av og delvis løsning på denne oppgaven
DEL EN
Oppgave 1
a)
$f(x)= 2x^2-5x-6 \\ f'(x) = 4x-5$
b)
$g(x)= xlnx\\ g'(x)= lnx + x \cdot \frac 1x = lnx + 1$
c)
$h(x)=\frac {e^{2x}}{x-3} \\ h'(x)= \frac{2e^{2x} (x-3)- e^{2x}}{(x-3)^2} = \frac{(2x-7)e^{2x}}{(x-3)^2}$
Oppgave 2
a)
$f(x)=0 \\ (x+1)^2(x-2) \\ x=-1 \vee x=2$
Nullpunkter: (-1, 0) og (2, 0)
b)
$f'(x)=0 \\ f'(x) = 2(x+1)(x-2) + (x+1)^2 = (x+1)(3x-3) \\ x =-1 \vee x= 1$
f'(-2) > 0, f'(0) < 0 og f'(2) > 0 gir toppunkt i ( -1, 0) og minimum for (1,-4 ).
c)
Oppgave 3
a)
$\frac{2x + 10}{x^2-25} +\frac{x}{x+5} - \frac {4}{2x - 10}= \\\frac{2x + 10}{(x+5)(x-5)} +\frac{x}{x+5} - \frac {4}{2(x-5)}= \\ \frac{4x+20+2x(x-5) - 4(x+5)}{2(x+5)(x-5) } = \\ \frac{2x(x-5)}{2(x+5)(x-5)} = \\ \frac{x}{x+5}$
b)
$\frac{2x+10}{x^2-25} + \frac{x}{x+5} = \frac{4}{2x-10} \\ 2(2x+10) + 2x(x-5) = 4(x+5) \\ 4x+20+2x^2-10x = 4x + 20 \\2x^2-10x=0 \\ x=0 \vee 2x-10=0 \\ x= 0 \vee x= 5$
Må forkaste x = 5, da det gir null i nevner.
L={ 0 }
En mere elegant og tidsbesparende løsning er å løse svaret fra a lik null:
$\frac {x}{x+5} =0$
som gir x=0 direkte.
Oppgave 4
a)
$2^{3x-2} - 13 = 3 \\ 2^{3x-2} = 2^4 \\ 3x-2 = 4 \\ 3x=6 \\ x=2$
b)
$ (lgx)^2 +lgx-2=0 \\ u=lgx\\ u^2+u-2 =0 \\ ABC- formel \\ u= -2 \vee u = 1 \\ lgx = -2 \vee lgx =1 \\ x=0,01 \vee x= 10$
Oppgave 5
a)
[ 1, 1] er parallell med AB vektor:
<math> \left[ \begin{align*}x = -4 + t\\ y = 5+ t \end{align*}\right] </math>
b)
Skjærer x - aksen betyr at y = 0. Da må t være - 5.
Da blir x = -9
D ( -9, 0)
c)
$[1, 1] \cdot [-3+4-t, -2-5-t] =0 \\ 1 -t - 7 - t =0 \\ t=-3 \\ x= -7 \wedge y=2$
E ( -7, 2)
Oppgave 6
a)
$P(D|A)= 0,04 \\ P(D|B)= 0,01 \\ P(A) = \frac 13 \\ P(B)= \frac 23$
Total sannsynlighet for defekt nøkkel
$P(D)= P(A) \cdot P(D|A) + P(B) \cdot P(D|B) \\ P(D)= \frac 13 \cdot 0,04 + \frac 23 \cdot 0,01 = 0,06 :3 = 0,02 $
Det er 2% sannsynlig at nøkkelen er defekt.
b)
$P(D) \cdot P(A|D) = P(A) \cdot P(D|A) \\ P(A|D)= \frac{P(A) \cdot P(D|A)}{P(D)} = \frac 13 \cdot \frac {0,04}{0,02} = \frac 23$
Det er ca. 67% sannsynlig at en defekt nøkkel kommer fra maskin A.
Oppgave 7
a)
$ \triangle PCB$ er likebeint, derfor er $\angle PCB = v $
$\angle PCE$ er 90 grader fordi toppunktet ligger på periferien og den spenner over 180 grader av sirkelsektoren.
$ \angle ABC$ er også 90 grader, derfor må $\angle ACE = v. $
$ \angle A$ er felles i begge trekantene og $\angle ACE = \angle PCB = v$, derfor er trekantene formlike.
b)
$AB= c, \quad EB=a \\ AE = AB - EB = c-a \\ BP = a, \quad AB= c \\ AP = AB + BP = c+a $
c)
Forholdet mellom samsvarende sider i formlike trekanter er likt.
$\frac{AP}{AC} = \frac{AC}{AE} \\ \frac{c+a}{b} = \frac{b}{c-a}$
d)
$\frac{c+a}{b} = \frac{b}{c-a} \\ (c+a)= \frac {b^2}{c-a} \\ (c+a)(c-a) =b^2 \\ c^2- ab + ab - a^2 = b^2 \\ a^2 + b^2 = c^2 $
Oppgave 8
(ii) er grafen til funksjonen. Den har minimumspunkt for x=0 og vender sin hule side opp hele tiden, dvs. ingen vendepunkter.
(i) er grafen til f'(x). Den er null origo når f(x) har et minimum. (iii) er grafen til den dobbeltderiverte.
DEL TO
Oppgave 1
a)
${34\choose7} = _{34}C_7 = 5 379 616 $
b)
Hypergeometrisk situasjon:
P (nøyaktig fem rette) $ = \frac{{7\choose5}\cdot {27 \choose 2}}{ {34\choose7} } \approx 0,0014$ , eller 0,14% sannsynlig.
c)
Sannsynligheten for at de tre siste tallene går inn er:
$ = \frac{{3\choose3}\cdot {27 \choose 0}}{ {30\choose3} } \approx 0,0002$ , eller 0,02%.
Oppgave 2
a)
Sirkel $C_1 \quad \quad $ Sentrum: $S_1( -5, 0) \quad $ , Radius: $r_1 = \sqrt{80} = 4 \sqrt 5$
Sirkel $C_2 \quad \quad $ $ \quad x^2-10x+y^2+5=0 \\ x^2 - 10x + 5^2 + y^2 + 5 = 5^2 \\ (x-5)^2+y^2 =20 \\ \\ Sentrum: \quad S_2 (5, 0) \quad \quad Radius: \quad r_2 = \sqrt{20} = 2 \sqrt 5$
b)
Skjæringspunktene er ( 3, 4 ) og ( 3, -4 ).
c)
Dersom ortogonale er skalarproduktet mellom vektorene null.
$ \vec{AC} \cdot \vec{CB} = 0 \\ [8,4] \cdot [2, -4] = 16 + ( -16)= 0 $
Sirklene er ortogonale.
Oppgave 3
a)
Fra ungdomsskolen: $ s = vt \\ t = \frac sv $
x er lengden langs veien og 5 er farten langs veien. Tidsforbruk langs vei: $t_v(x)= \frac x5$ Rotuttrykket i andre ledd er lengden av hypotenusen BH (altså lengden hun beveger seg i terrenget), uttrykt ved katetene i den rettvinklede trekanten BCH. 3 er farten i terrenget. Derav uttrykket.
b)
Vi ser at hun bruker kortest tid om hun skjærer av vegen etter 3,5 km. Hun bruker da 1,53 timer, eller 1 time 31 minutter og 48 sekunder, for å være nøyaktig.
Oppgave 4
a)
b)
$ \vec r(t)= [t^3-3t+3, t-1] \quad \quad -2 \leq x \leq 2 \\ \vec v(t) = \vec r ' (t)= [3t^2-3,1] \\ \vec a(t)= \vec r ' ' (t) = [6t, 0] $
Når t =1
$ Posisjon:\quad \vec r(1)= [1^3-3 \cdot 1+3, 1-1] = [1,0] \\ Banefart: | \vec v(1)| = [3 \cdot 1^2-3,1] = |[0,1]| = 1 \\ Akselerasjon:| \vec a(1)|= =| [6 \cdot 1, 0]| =6 $
Når t = 1 er posisjonen (1,0), banefarten lik 1 og akselerasjonen lik 6.
c)
Fartsvektor parallell med y aksen:
$ \vec v(t) || [0, 1] \\ [3t^2-3] = k[0, 1] \\ 3t^2 - 3 =0 \\ t^2 =1 \\ t = \pm 1$
Setter t verdiene inn i posisjonsvektoren:
t = 1 har vi fra b : [1,0]
t = -1 gir oss $[-1 +3+3, -2 ] = [5, -2]$
Oppgave 5
Skjæring mellom parabel og sirkel (sentrum i origo og radius fem) gir de fire punktene vist over.