1P 2016 høst LØSNING: Forskjell mellom sideversjoner
| (60 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/download/file.php?id= | [http://www.matematikk.net/matteprat/download/file.php?id=1329 Denne oppgaven som pdf] | ||
[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=44258 Diskusjon av denne oppgaven på matteprat] | [http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=44258 Diskusjon av denne oppgaven på matteprat] | ||
| Linje 24: | Linje 24: | ||
$\frac 25 = \frac6x \\ 2x=30 \\ x=15$ | $\frac 25 = \frac6x \\ 2x=30 \\ x=15$ | ||
Det ligger | Det ligger 15 basketballer i kassen, tilsammen 21baller. | ||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 46: | Linje 46: | ||
===a)=== | ===a)=== | ||
$kroneverdi = \frac{100}{KPI}$ | |||
Når KPI øker blir kroneverdien mindre. Kroneverdi multiplisert med KPI er alltid 100. | |||
===b)=== | ===b)=== | ||
Nei, det er ikke riktig. Om vi deler 100 på 1,2 (som tilsvarer en KPI økning på 20%) ser man at kronen svekkes med ca 16,7%. | |||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 73: | Linje 78: | ||
Omkrets av figur : $O= 2AB + 2BC + \pi \cdot r \\ O \approx 20 + 24 + 3 \cdot 6 \\O \approx 62 $ | |||
Høyden fra BE til A: $ h = \sqrt{100 - 36} = 8$ | |||
Areal av figur: $A = \frac 12 \cdot BC \cdot h + BC \cdot BE + \frac{\pi \cdot r^2}{2} \\ A \approx 0,5 \cdot 12 \cdot 8 + 12 \cdot 12 + \frac{3 \cdot 6^2}{2} \\ A \approx 48 + 144 + 54 \\ A \approx 246 $ | Areal av figur: $A = \frac 12 \cdot BC \cdot h + BC \cdot BE + \frac{\pi \cdot r^2}{2} \\ A \approx 0,5 \cdot 12 \cdot 8 + 12 \cdot 12 + \frac{3 \cdot 6^2}{2} \\ A \approx 48 + 144 + 54 \\ A \approx 246 $ | ||
| Linje 92: | Linje 97: | ||
==Oppgave 10== | ==Oppgave 10== | ||
===a)=== | |||
$P(BRR) = \frac{4}{8} \cdot \frac{4}{7} \cdot \frac{3}{6} = \frac 17$ | |||
===b)=== | |||
Det er tre posisjoner for blå nisse: P( en blå og to røde)$ = 3 \cdot \frac 17 = \frac 37$ | |||
===c)=== | |||
Dersom vi IKKE har minst en blå har vi tre røde. Sannsynligheten for det er: | |||
P( bare røde)=$ \frac 48 \cdot \frac 37 \cdot \frac 26 = \frac{1}{14}$ | |||
Sannsynligheten for minst en blå blir da: | |||
P( minst en rød) = $1- \frac{1}{14} = \frac{13}{14}$ | |||
==Oppgave 11== | ==Oppgave 11== | ||
| Linje 108: | Linje 132: | ||
Ved kjøp av fire drikke vil det lønne seg å kjøpe kopp. | Ved kjøp av fire drikke vil det lønne seg å kjøpe kopp. | ||
[[File:1p-h2016-1-11c.png]] | |||
==DEL TO== | ==DEL TO== | ||
==Oppgave 1== | |||
===a)=== | |||
[[File:1p-h2016-2-1a.png]] | |||
===b)=== | |||
Fra figuren i a ser man at klokka 06:55 passerer det ca 83 biler per minutt. | |||
===c)=== | |||
Fra figuren i a ser man at det passerer mere enn 70 biler per minutt i tidsrommet 06:27 til 07:32. | |||
==Oppgave 2== | |||
===a)=== | |||
Vinkel B er lik vinkel E. | |||
Vinkel C i begge er like fordi de er toppvinkler. Da er vinkel A lik vinkel D og trekantene er formlike. | |||
===b)=== | |||
Forholdet mellom sidene i ABC og CDE er $\frac{74,2}{53} = 1,4$ | |||
BC: $\frac{x}{28} =1,4 \\ x = 1,4 \cdot 28 = 39,2$ | |||
Lengden av BC er 39,2. | |||
AB: $(74,2)^2 = (AB)^2 + (39,2)^2 \\ AB = \sqrt{5505,64 - 1536,64}\\ AB = 63$ | |||
===c)=== | |||
Forhold mellom areal: | |||
Forholdet mellom sidene i trekantene er 1,4 og arealet av en trekant er $A= \frac 12 gh$ | |||
$\frac{A_{stor}}{A_{liten}} = (1,4)^2 = 1,96$ | |||
Den store trekanten har 1,96 ganger så stort areal som den lille. | |||
==Oppgave 3== | |||
Dersom reallønnen er uendret er kjøpekraften opprettholdt. | |||
$ Reallønn = lønn \cdot \frac{100}{KPI} \\ 520800 \cdot \frac{100}{139,8} = 375532$ | |||
Dersom reallønnen i 2016 er 375 532 kroner er kjøpekraften opprettholdt. | |||
==Oppgave 4== | |||
$850000 \cdot 0,800 \cdot 0,965^5 = 569043,5$ | |||
Etter seks år har båten en verdi på ca, 570 000 kroner. | |||
==Oppgave 5== | |||
===a)=== | |||
Overflate kiste: | |||
Bunn $ 0,41m \cdot 0,95 m = 0,3895m^2 $ | |||
Forside og bakside: $2 \cdot 0,95m \cdot 0,62 m = 1,178 m^2$ | |||
Sidekanter: $2 \cdot 0,41m \cdot 0,62m = 0,5082m^2$ | |||
Lokk: $\frac {2 \pi r^2}{2} + l \cdot \frac{2\pi r}{2} = \pi (0,205m)^2 + 0,95 \cdot \pi \cdot 0,205 m^2 = 0,744m^2$ | |||
Legger vi sammen alle delsvarene får man 2,82 $ m^2$. Det betyr at han trenger ca. 2,82 dl, dersom han ikke søler med malingen. | |||
===b)=== | |||
Innvendig volum. | |||
Prisme: $V = lbh = 92cm \cdot 38 cm \cdot 60,5cm = 211508 cm^3$ | |||
Lokk: $V= \frac 12 \pi r^2 \cdot l = 0,5 \cdot \pi \cdot(19cm)^2 \cdot 92 = 52169 cm^3$ | |||
Legger vi sammen og gjør om til kubikk meter får man ca. 263700 $cm^3$ som er ca. 0,26 $m^3$ | |||
==Oppgave 6== | |||
===a) b) c)=== | |||
[[File:1p-h2016-2-6a1.png]] | |||
[[File:1p-h2016-2-6a2.png]] | |||
==Oppgave 7== | |||
===a)=== | |||
Økningen var fra ca. 40 kg i 1970 til ca 60 kg i 2000. En økning på 20 kg, $\frac {20}{40} = 0,50$. Økningen var på ca 50 %. | |||
===b)=== | |||
I denne perioden har grafen form som en rett linje, altså lineær vekst. | |||
===c)=== | |||
Tidsperioden er 20 år. Veksten anslåes til å være ca. 33 kg i denne perioden, dvs en økning på 1,65 kg per år. I 1954 er forbruket ca 41 kg. Vi får da: | |||
y= 1,65x + 41 | |||
==Oppgave 8== | |||
===a)=== | |||
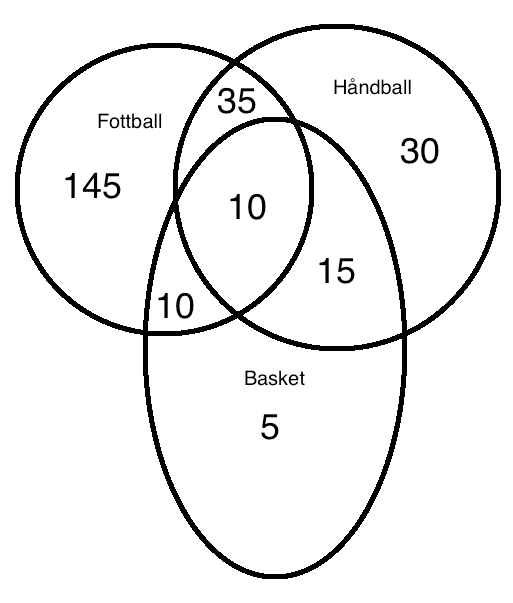
Basketball og håndball er: 90 - 30 - 35 - 10 = 15 | |||
160 medlemmer spiller bare fotball og / eller basketball. Det betyr at 10 gjør begge deler: | |||
[[File:1p-h2016-2-8a.png]] | |||
===b)=== | |||
$ P( F \cap H \cap B) = \frac{10}{250} = \frac {1}{25}= $ 4% | |||
Det er fire prosent sannsynlighet for å velge en som driver med alle tre idrettene. | |||
===c)=== | |||
$P(F| H) = \frac{45}{90} = \frac 12$ | |||
Det er 50% sannsynlighet for at en som driver med håndball også spiller fotball. | |||
==Oppgave 9== | |||
Vi ser at dersom 12 går sammen må hver betale 1000 kroner. Trampolina koster 12000 kroner. | |||
12 000 kr : 25 = 480 kroner. | |||
Dersom 25 går sammen må hver av dem betale 480 kroner. | |||
Siste sideversjon per 4. nov. 2017 kl. 06:31
Diskusjon av denne oppgaven på matteprat
Mer diskusjon av denne oppgaven på matteprat
DEL EN
Oppgave 1
$8: \frac 23 = \frac{8 \cdot 3}{2} = 12$
Jeg trenger 12 bokser.
Oppgave 2
$\frac{5cm}{1,5km} = \frac 1x \\ \Downarrow \\ \frac{5cm}{150000cm } = \frac 1x \\ \Downarrow \\ x= \frac{150000}{5} = 30000$
Målestokken på kartet er 1: 30 000.
Oppgave 3
$\frac 25 = \frac6x \\ 2x=30 \\ x=15$
Det ligger 15 basketballer i kassen, tilsammen 21baller.
Oppgave 4
a)
$\frac 15 = \frac {2}{10} = \frac{20}{ 100} = 20$ %
$\frac{135}{250} = \frac{540}{1000} = \frac{54}{100} = 54$ %
b)
$\frac 15 \cdot \frac 34 = \frac {3}{20} = \frac{15}{100} = 15$ %
Det er 15% av elevene som spiller håndball.
Oppgave 5
a)
$kroneverdi = \frac{100}{KPI}$
Når KPI øker blir kroneverdien mindre. Kroneverdi multiplisert med KPI er alltid 100.
b)
Nei, det er ikke riktig. Om vi deler 100 på 1,2 (som tilsvarer en KPI økning på 20%) ser man at kronen svekkes med ca 16,7%.
Oppgave 6
$ AB = \sqrt{7,0^2 + 6,0^2} = \sqrt{85}$
Siden kvadratroten av 81 er 9 vil lengden AB være noe lengre enn 9,0 meter.
Oppgave 7
a)
$y=kx \Rightarrow k = \frac yx = \frac{350 kr}{50 kg} = \frac{700 kr}{100 kg} = \frac{1750kr}{250kg} = \frac{2800kr}{400kg} = 7 $ kr/kg
b)
Pris: y (kroner)
Mengde x (kilogram)
y=7x
Oppgave 8
Omkrets av figur : $O= 2AB + 2BC + \pi \cdot r \\ O \approx 20 + 24 + 3 \cdot 6 \\O \approx 62 $
Høyden fra BE til A: $ h = \sqrt{100 - 36} = 8$
Areal av figur: $A = \frac 12 \cdot BC \cdot h + BC \cdot BE + \frac{\pi \cdot r^2}{2} \\ A \approx 0,5 \cdot 12 \cdot 8 + 12 \cdot 12 + \frac{3 \cdot 6^2}{2} \\ A \approx 48 + 144 + 54 \\ A \approx 246 $
Oppgave 9
a)
$K(x)= x^2+ b \cdot x +20000 \\ K(0) = 20000$
Det betyr at de faste kostnadene er 20000 kroner. Altså kostnader før man har produsert en eneste enhet.
b)
$30000 = 50^2 + 50b + 20000 \\ 50b = 30000 - 20000 - 2500 \\ 50b = 7500 \\ b= 150$
Oppgave 10
a)
$P(BRR) = \frac{4}{8} \cdot \frac{4}{7} \cdot \frac{3}{6} = \frac 17$
b)
Det er tre posisjoner for blå nisse: P( en blå og to røde)$ = 3 \cdot \frac 17 = \frac 37$
c)
Dersom vi IKKE har minst en blå har vi tre røde. Sannsynligheten for det er:
P( bare røde)=$ \frac 48 \cdot \frac 37 \cdot \frac 26 = \frac{1}{14}$
Sannsynligheten for minst en blå blir da:
P( minst en rød) = $1- \frac{1}{14} = \frac{13}{14}$
Oppgave 11
a)
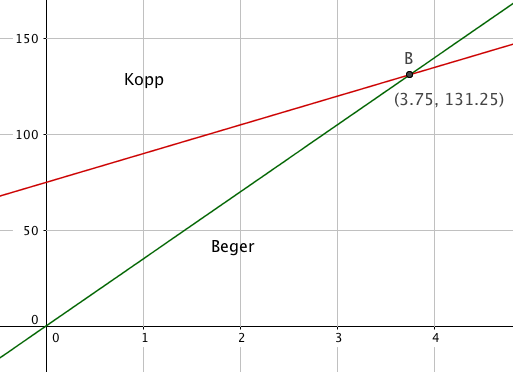
$f(x)= 35x$
b)
g(x)= 90 + 15(x-1) = 15x + 75
c)
$f(x) = g(x) \\ 35x = 15x + 75 \\ 20x = 75 \\ x = 3,75$
Ved kjøp av fire drikke vil det lønne seg å kjøpe kopp.
DEL TO
Oppgave 1
a)
b)
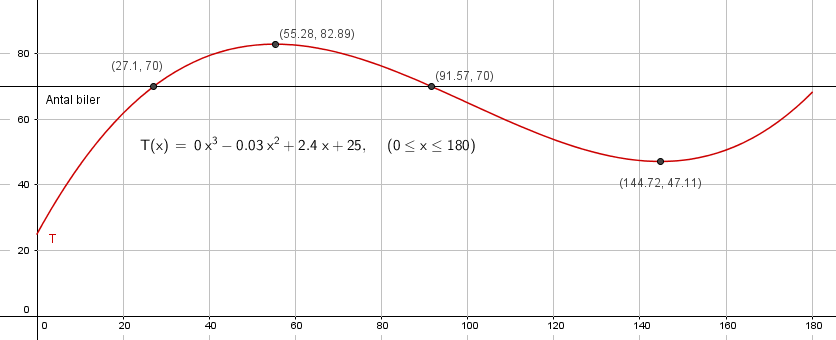
Fra figuren i a ser man at klokka 06:55 passerer det ca 83 biler per minutt.
c)
Fra figuren i a ser man at det passerer mere enn 70 biler per minutt i tidsrommet 06:27 til 07:32.
Oppgave 2
a)
Vinkel B er lik vinkel E.
Vinkel C i begge er like fordi de er toppvinkler. Da er vinkel A lik vinkel D og trekantene er formlike.
b)
Forholdet mellom sidene i ABC og CDE er $\frac{74,2}{53} = 1,4$
BC: $\frac{x}{28} =1,4 \\ x = 1,4 \cdot 28 = 39,2$
Lengden av BC er 39,2.
AB: $(74,2)^2 = (AB)^2 + (39,2)^2 \\ AB = \sqrt{5505,64 - 1536,64}\\ AB = 63$
c)
Forhold mellom areal:
Forholdet mellom sidene i trekantene er 1,4 og arealet av en trekant er $A= \frac 12 gh$
$\frac{A_{stor}}{A_{liten}} = (1,4)^2 = 1,96$
Den store trekanten har 1,96 ganger så stort areal som den lille.
Oppgave 3
Dersom reallønnen er uendret er kjøpekraften opprettholdt.
$ Reallønn = lønn \cdot \frac{100}{KPI} \\ 520800 \cdot \frac{100}{139,8} = 375532$
Dersom reallønnen i 2016 er 375 532 kroner er kjøpekraften opprettholdt.
Oppgave 4
$850000 \cdot 0,800 \cdot 0,965^5 = 569043,5$
Etter seks år har båten en verdi på ca, 570 000 kroner.
Oppgave 5
a)
Overflate kiste:
Bunn $ 0,41m \cdot 0,95 m = 0,3895m^2 $
Forside og bakside: $2 \cdot 0,95m \cdot 0,62 m = 1,178 m^2$
Sidekanter: $2 \cdot 0,41m \cdot 0,62m = 0,5082m^2$
Lokk: $\frac {2 \pi r^2}{2} + l \cdot \frac{2\pi r}{2} = \pi (0,205m)^2 + 0,95 \cdot \pi \cdot 0,205 m^2 = 0,744m^2$
Legger vi sammen alle delsvarene får man 2,82 $ m^2$. Det betyr at han trenger ca. 2,82 dl, dersom han ikke søler med malingen.
b)
Innvendig volum.
Prisme: $V = lbh = 92cm \cdot 38 cm \cdot 60,5cm = 211508 cm^3$
Lokk: $V= \frac 12 \pi r^2 \cdot l = 0,5 \cdot \pi \cdot(19cm)^2 \cdot 92 = 52169 cm^3$
Legger vi sammen og gjør om til kubikk meter får man ca. 263700 $cm^3$ som er ca. 0,26 $m^3$
Oppgave 6
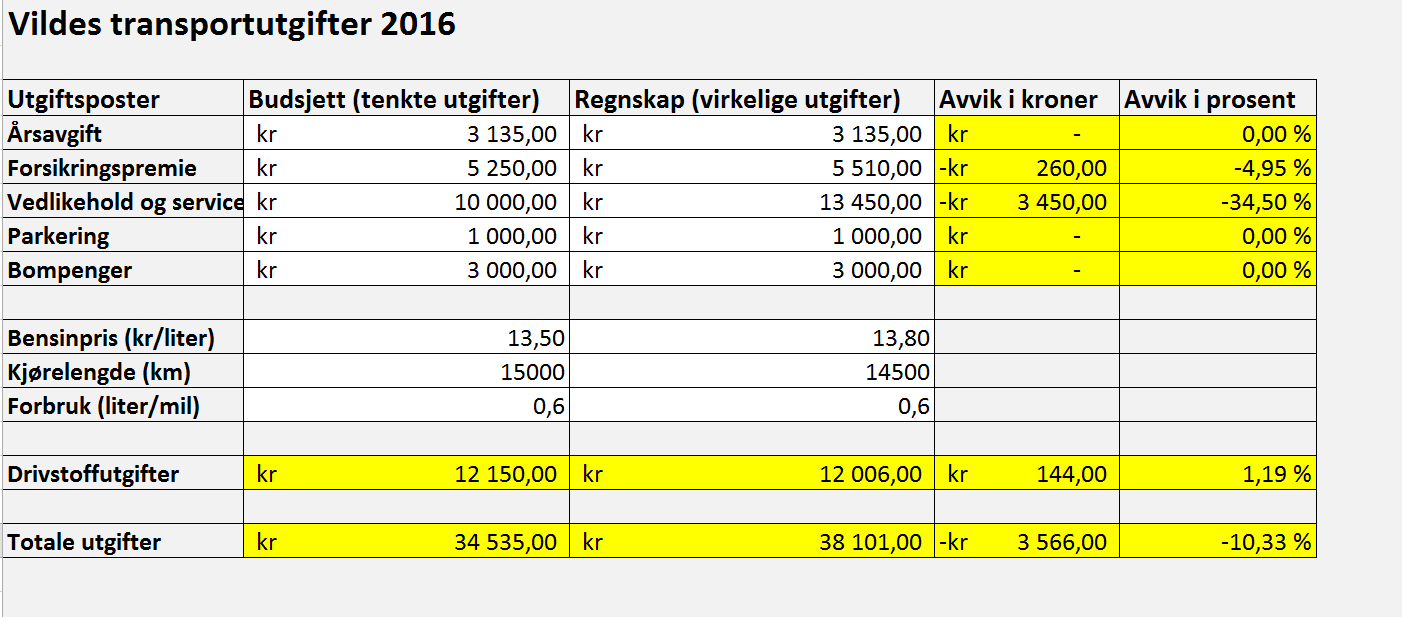
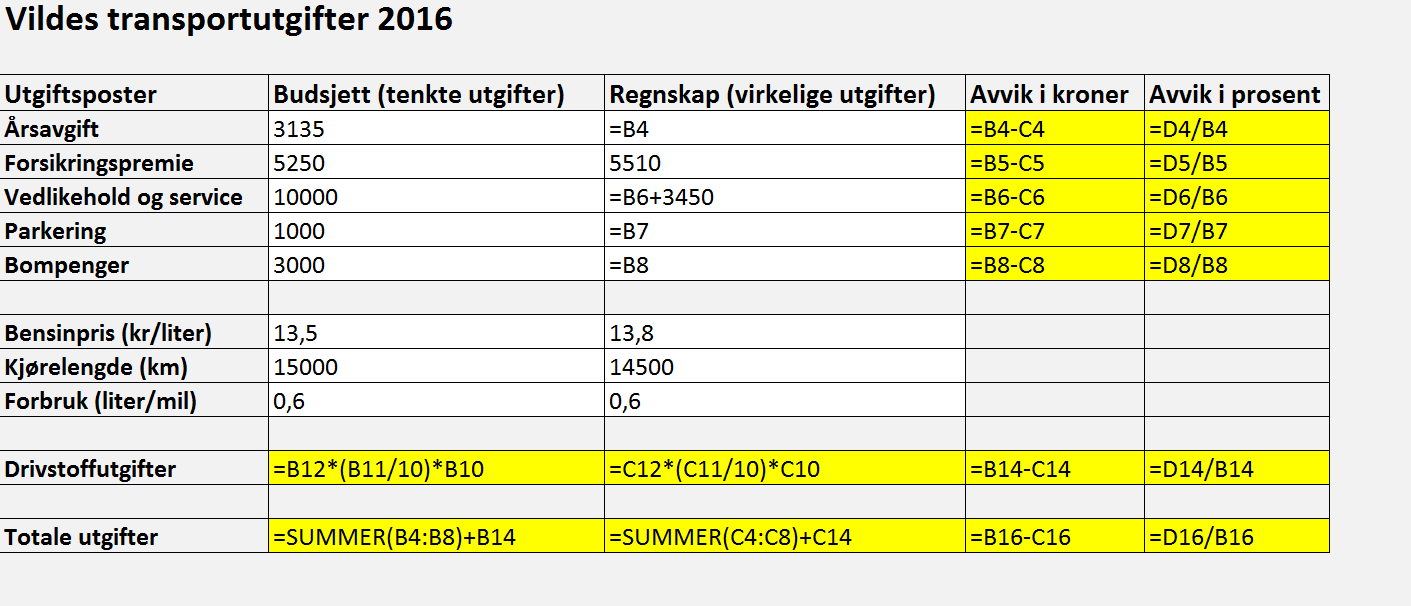
a) b) c)
Oppgave 7
a)
Økningen var fra ca. 40 kg i 1970 til ca 60 kg i 2000. En økning på 20 kg, $\frac {20}{40} = 0,50$. Økningen var på ca 50 %.
b)
I denne perioden har grafen form som en rett linje, altså lineær vekst.
c)
Tidsperioden er 20 år. Veksten anslåes til å være ca. 33 kg i denne perioden, dvs en økning på 1,65 kg per år. I 1954 er forbruket ca 41 kg. Vi får da:
y= 1,65x + 41
Oppgave 8
a)
Basketball og håndball er: 90 - 30 - 35 - 10 = 15
160 medlemmer spiller bare fotball og / eller basketball. Det betyr at 10 gjør begge deler:
b)
$ P( F \cap H \cap B) = \frac{10}{250} = \frac {1}{25}= $ 4%
Det er fire prosent sannsynlighet for å velge en som driver med alle tre idrettene.
c)
$P(F| H) = \frac{45}{90} = \frac 12$
Det er 50% sannsynlighet for at en som driver med håndball også spiller fotball.
Oppgave 9
Vi ser at dersom 12 går sammen må hver betale 1000 kroner. Trampolina koster 12000 kroner.
12 000 kr : 25 = 480 kroner.
Dersom 25 går sammen må hver av dem betale 480 kroner.