Sinusfunksjonen: Forskjell mellom sideversjoner
| (46 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
===Fra graf til funksjonsuttrykk=== | |||
Generellt ser uttrykket til en sinusfunksjon slik ut: | |||
$f(x) = A sin(kx+c) + d$ | $f(x) = A sin(kx+c) + d$ | ||
| Linje 7: | Linje 9: | ||
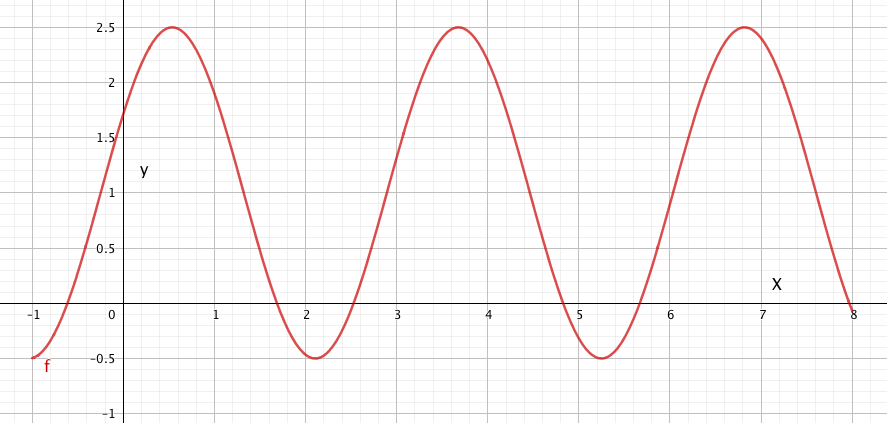
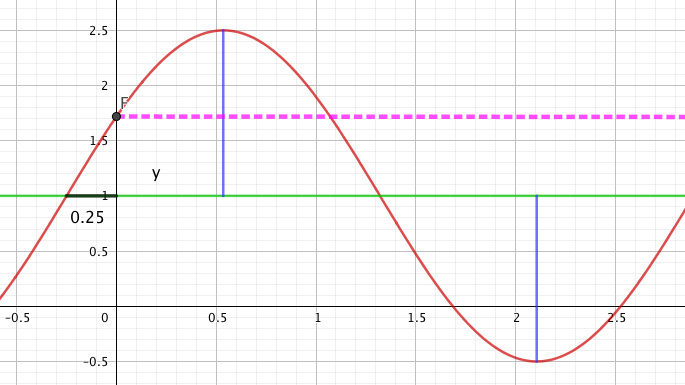
Hvordan kan vi knytte dette funksjonsuttrykket sammen med en graf som ser slik ut?: | Hvordan kan vi knytte dette funksjonsuttrykket sammen med en graf som ser slik ut?: | ||
[[File: | |||
[[File:sinrev-22.png]] | |||
===Likevektslinje=== | ===Likevektslinje=== | ||
| Linje 15: | Linje 18: | ||
Likevektslinje: y = d | Likevektslinje: y = d | ||
Vi finner uttrykket for d ved å regne ut: $d= \frac{f_{maks}+ f_{min}}{2}= \frac{5+(- | Vi finner uttrykket for d ved å regne ut: $d= \frac{f_{maks}+ f_{min}}{2}= \frac{2,5+(-0,5)}{2} = 1$ | ||
[[File:sinrev2-22.png]] | |||
===Amplitude: A === | |||
Amplituden er det største utslaget på grafen. Når du skrur på volumet på stereoen din bestemmer du amplituden. Dersom du ønsker høy lyd er aplituden stor.. | |||
Amplituden er utslaget fra likevekstlinja, og er alltid positivt. | |||
Amplitude: $\quad f_{max}- d = 2,5-1 = 1,5 $ | |||
[[File:sinrev3-22.png]] | |||
[[File: | |||
Man må | Man må merke seg at amplituden er en absoluttverdi, den er alltid positiv fordi den måler avstanden fra likevekstlinje til maksimalt (eller minimalt) utslag. | ||
Amplituden er lengden av den blå linjen. Den | Amplituden er lengden av den blå linjen. Den grønne linjen er likevekstlinjen. | ||
Da har vi etablert at modellen ser slik ut: $f(x)= | Da har vi etablert at modellen ser slik ut: $f(x)=1,5 sin(kx+c) +1$ | ||
Vi | Vi mangler fortsatt k og c. | ||
===Periode=== | ===Periode=== | ||
Peiode P: $ | Hvor mange ganger funksjonen repeterer seg selv i intervallet $2 \pi$ multiplisert med lengden av repetisjonen gir: | ||
$pk = 2 \pi$ | |||
Peiode P: $ p = \frac {2 \pi}{k} , \quad \quad \quad \quad Antall \, repetisjoner\, i \ 2\pi: k= \frac{2\pi}{p}$ | |||
k er gjentakelser i intervallet $2 \pi$ og p er lengden av perioden. | |||
[[File:sinrev4-22.png]] | |||
Den stiplede linjen viser gjentakelsene av funksjonen en fra F til G, og en fra G til E, altså k = 2. | |||
k er antallet ganger funksjonen repeterer seg selv i intevallet $2 \pi$. Fra figuren ser man at k = 2 og at lengden på peroden blir $\pi$ | k er antallet ganger funksjonen repeterer seg selv i intevallet $2 \pi$. Fra figuren ser man at k = 2 og at lengden på peroden blir $\pi$ | ||
===Faseforskyvning=== | ===Faseforskyvning=== | ||
sin (x) og sin (kx) vil være null for x = 0, for så å vokse med økende x. Ved faseforskyvning blir grafen forskjøvet. | |||
Vi finner skjæring med likevektslinje ved å sette | |||
kx + c= 0 | |||
Faseforskyvning: $\quad x =- \frac{c}{k}$ | |||
[[File:sinrev5-22.png]] | |||
Man observere at faseforskyvningen er -0,25. Vi tar utgangspunkt i punktet der likevektslinjen krysser y aksen og beveger oss til den delen av grafen som vokser, fordi sinusfunksjonen vokser for vinkler i første kvadrant. Se fuguren over. | |||
Da blir c: $ kx +c =0 \Rightarrow c= - kx \Rightarrow c= -2 \cdot(- \frac14) = \frac 12$ | |||
Dersom $c<0$ forskyves grafen mot høyre. | Dersom $c<0$ forskyves grafen mot høyre. | ||
| Linje 62: | Linje 84: | ||
'''Funksjonsutrykket ser slik ut: $f(x)= | '''Funksjonsutrykket ser slik ut: $f(x)= \frac 32sin(2x+ \frac{1}{2}) +1$ | ||
Dersom vi faktoriserer uttrykket man skal ta sinus av får man | |||
$f(x)= \frac 32 sin(2(x + \frac 14)) +1$ | |||
Her ser man at faseforskyvningen vises eksplisit. | |||
==Litt mere om faseforskyvning== | ==Litt mere om faseforskyvning== | ||
| Linje 75: | Linje 103: | ||
[[File:sin-6.png]] | [[File:sin-6.png]] | ||
==Nullpunkt for sinusfunksjonen== | |||
For å finne nullpunktene til sinusfunksjonen må man kunne løse likninger, fordi man som vanlig setter $f(x)=0$ | |||
Trigonometriske likninger finner du her [[https://matematikk.net/side/Trigonometriske_likninger#Trigonometriske_likninger]]. | |||
== Ekstremalpunkt for sinusfunksjonen== | |||
Man kan derivere funksjonen og sette den deriverte lik null, men ofte er det lettere å benytte egenskapene ved sinusfunksjonen. | |||
Vi vet at sin( u) antar verdier fra -1 til 1. | |||
Vi har funksjonen $g(x) = 3sin(2x- \frac{\pi}{4})-1 \quad D_g= [0, 3 \pi>$ | |||
===toppunkt=== | |||
Vi vet funksjonen har sin (u) maksimale verdi lik 1 når $u= \frac {\pi}{2}$ | |||
$2x- \frac{\pi}{4} = \frac {\pi}{2}$ | |||
Så må vi ta hensyn til at definisjonsmengden går fra 0 til $3 \pi$ og får: | |||
$2x- \frac{\pi}{4} = \frac {\pi}{2} + 2 \pi k \\ 8x - \pi = 2 \pi + 8k \pi \\ x = \frac{3 \pi}{8} +k \pi \\ k=0 \, gir \, x=\frac{3 \pi}{8} \\ k=1 \, gir \, x=\frac{11 \pi}{8} \\ k=2 \, gir \, x=\frac{19 \pi}{8}\\ $ | |||
k = 4 kommer over øvre grensen til definisjonsmengden, og skal ikke være med. | |||
Siste sideversjon per 23. sep. 2018 kl. 12:41
Fra graf til funksjonsuttrykk
Generellt ser uttrykket til en sinusfunksjon slik ut:
$f(x) = A sin(kx+c) + d$
Hvordan kan vi knytte dette funksjonsuttrykket sammen med en graf som ser slik ut?:
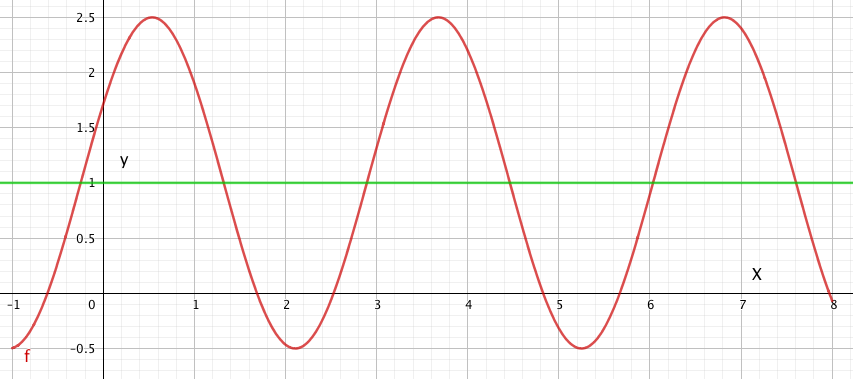
Likevektslinje
Likevektslinjen er den linjen den periodiske funksjonen svinger rundt. Utslaget er like stort til begge sider (opp og ned).
Likevektslinje: y = d
Vi finner uttrykket for d ved å regne ut: $d= \frac{f_{maks}+ f_{min}}{2}= \frac{2,5+(-0,5)}{2} = 1$
Amplitude: A
Amplituden er det største utslaget på grafen. Når du skrur på volumet på stereoen din bestemmer du amplituden. Dersom du ønsker høy lyd er aplituden stor..
Amplituden er utslaget fra likevekstlinja, og er alltid positivt.
Amplitude: $\quad f_{max}- d = 2,5-1 = 1,5 $
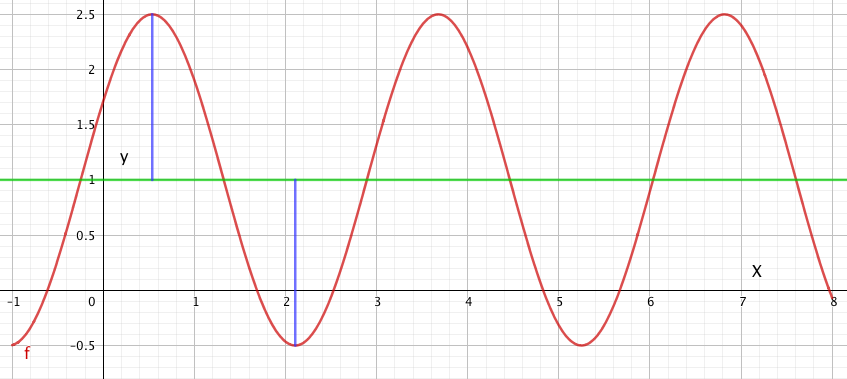
Man må merke seg at amplituden er en absoluttverdi, den er alltid positiv fordi den måler avstanden fra likevekstlinje til maksimalt (eller minimalt) utslag.
Amplituden er lengden av den blå linjen. Den grønne linjen er likevekstlinjen.
Da har vi etablert at modellen ser slik ut: $f(x)=1,5 sin(kx+c) +1$
Vi mangler fortsatt k og c.
Periode
Hvor mange ganger funksjonen repeterer seg selv i intervallet $2 \pi$ multiplisert med lengden av repetisjonen gir:
$pk = 2 \pi$
Peiode P: $ p = \frac {2 \pi}{k} , \quad \quad \quad \quad Antall \, repetisjoner\, i \ 2\pi: k= \frac{2\pi}{p}$
k er gjentakelser i intervallet $2 \pi$ og p er lengden av perioden.
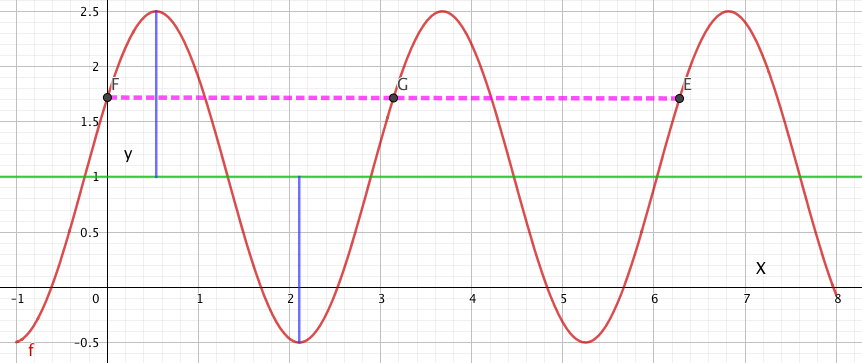
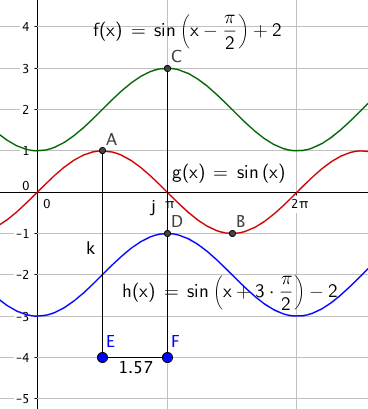
Den stiplede linjen viser gjentakelsene av funksjonen en fra F til G, og en fra G til E, altså k = 2.
k er antallet ganger funksjonen repeterer seg selv i intevallet $2 \pi$. Fra figuren ser man at k = 2 og at lengden på peroden blir $\pi$
Faseforskyvning
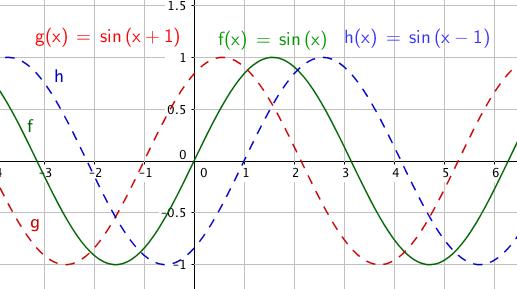
sin (x) og sin (kx) vil være null for x = 0, for så å vokse med økende x. Ved faseforskyvning blir grafen forskjøvet.
Vi finner skjæring med likevektslinje ved å sette
kx + c= 0
Faseforskyvning: $\quad x =- \frac{c}{k}$
Man observere at faseforskyvningen er -0,25. Vi tar utgangspunkt i punktet der likevektslinjen krysser y aksen og beveger oss til den delen av grafen som vokser, fordi sinusfunksjonen vokser for vinkler i første kvadrant. Se fuguren over.
Da blir c: $ kx +c =0 \Rightarrow c= - kx \Rightarrow c= -2 \cdot(- \frac14) = \frac 12$
Dersom $c<0$ forskyves grafen mot høyre.
Dersom $c> 0$ forskyves grafen mot venstre.
Funksjonsutrykket ser slik ut: $f(x)= \frac 32sin(2x+ \frac{1}{2}) +1$
Dersom vi faktoriserer uttrykket man skal ta sinus av får man
$f(x)= \frac 32 sin(2(x + \frac 14)) +1$
Her ser man at faseforskyvningen vises eksplisit.
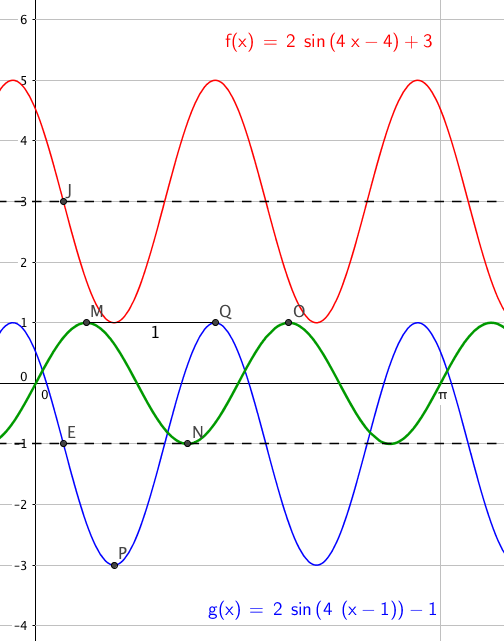
Litt mere om faseforskyvning
Alternativ skrivemåte
Nullpunkt for sinusfunksjonen
For å finne nullpunktene til sinusfunksjonen må man kunne løse likninger, fordi man som vanlig setter $f(x)=0$
Trigonometriske likninger finner du her [[1]].
Ekstremalpunkt for sinusfunksjonen
Man kan derivere funksjonen og sette den deriverte lik null, men ofte er det lettere å benytte egenskapene ved sinusfunksjonen.
Vi vet at sin( u) antar verdier fra -1 til 1.
Vi har funksjonen $g(x) = 3sin(2x- \frac{\pi}{4})-1 \quad D_g= [0, 3 \pi>$
toppunkt
Vi vet funksjonen har sin (u) maksimale verdi lik 1 når $u= \frac {\pi}{2}$
$2x- \frac{\pi}{4} = \frac {\pi}{2}$
Så må vi ta hensyn til at definisjonsmengden går fra 0 til $3 \pi$ og får:
$2x- \frac{\pi}{4} = \frac {\pi}{2} + 2 \pi k \\ 8x - \pi = 2 \pi + 8k \pi \\ x = \frac{3 \pi}{8} +k \pi \\ k=0 \, gir \, x=\frac{3 \pi}{8} \\ k=1 \, gir \, x=\frac{11 \pi}{8} \\ k=2 \, gir \, x=\frac{19 \pi}{8}\\ $
k = 4 kommer over øvre grensen til definisjonsmengden, og skal ikke være med.