Integral: Forskjell mellom sideversjoner
| (53 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
===3.1.1=== | |||
Formålet med denne siden er at de som har behovet skal få en viss forståelse for hva integrasjon og integraler er. Du må vite hva derivasjon er først. Dersom du ønsker en mer systematisk og matematisk behandling av emnet går du til [[Integrasjon#integrasjon| integrasjon ]] | |||
===3.1.2=== | |||
En moped beveger seg med konstant fart 4 meter per sekund. Grafisk kan det se slik ut: | En moped beveger seg med konstant fart 4 meter per sekund. Grafisk kan det se slik ut: | ||
| Linje 25: | Linje 29: | ||
===3.1.3=== | |||
En annen moped kjører med hastigheten 6 meter per sekund og begynner så å bremse opp. Mopeden bremser med en jevn akselerasjon (negativ) fra 6m/s til 1 m/s. Funksjonen som beskriver situasjonen ser slik ut: | |||
En annen moped | |||
g(t) = 6 - t | g(t) = 6 - t | ||
| Linje 36: | Linje 40: | ||
[[File:integral-2.png]] | [[File:integral-2.png]] | ||
I dette eksemplet ser vi at arealet under grafen er 17,5 og at benevningen er m (meter), hvilket betyr at mopeden beveger seg 17,5 under oppbremsingen. | I dette eksemplet ser vi at arealet under grafen er 17,5 og at benevningen er m (meter), hvilket betyr at mopeden beveger seg 17,5 meter under oppbremsingen. | ||
De to | De to eksemplene over var med rette linjer, altså lineære funksjoner. Hva da når grafen krummer? | ||
== | ===3.1.4=== | ||
For å finne arealet under krumme kurver kan vi dele området opp i rektangler som vist under | For å finne arealet under krumme kurver kan vi dele området opp i rektangler som vist under | ||
[[File:riemann.png]] | |||
Vi observerer følgende: | Vi observerer følgende: | ||
*Rektanglene under kurven i figur | *Rektanglene under kurven i figur A1 og A2 vil gi et større areal enn det som faktisk er under kurven. | ||
*Rektanglene under kurven i figur | *Rektanglene under kurven i figur B1 og B2 vil gi et mindre areal enn det som faktisk er under kurven. | ||
*Bredden av rektanglene og derved også antall rektangler, har betydning for nøyaktigheten i resultatet. Både modell A og B vil bevege seg mot arealet under kurven, når antall rektangler går mot uendelig, og bredden av rektanglene avtar. Arealet under kurven er summen av disse rektanglene. Bredden av et rektangel er gitt ved: | *Bredden av rektanglene og derved også antall rektangler, har betydning for nøyaktigheten i resultatet. Både modell A og B vil bevege seg mot arealet under kurven, når antall rektangler går mot uendelig, og bredden av rektanglene avtar. Arealet under kurven er summen av disse rektanglene. Bredden av et rektangel er gitt ved: | ||
$\Delta x = \frac{b-a}{n}$ | |||
Der n er antall rektangler, b er øvre grense og a er nedre grense som begrenser arealet under kurven. | Der n er antall rektangler, b er øvre grense og a er nedre grense som begrenser arealet under kurven. | ||
Summen $S_n$ av rektanglene under grafen blir: | |||
Summen | |||
$S_n = f(x_1)\cdot \Delta x + f(x_2) \cdot \Delta x+..+f(x_n) \cdot \Delta x$ (kalles '''Riemannsum''') | $S_n = f(x_1)\cdot \Delta x + f(x_2) \cdot \Delta x+..+f(x_n) \cdot \Delta x$ (kalles '''Riemannsum''') | ||
| Linje 65: | Linje 68: | ||
Det bestemte integralet til f er: | Det bestemte integralet til f er: | ||
$\int\limits_a^b f(x)dx = \lim_{ | $\int\limits_a^b f(x)dx = \lim_{n \to \infty}S_n$ | ||
Der f(x) er integranden, a er nedre integrasjonsgrense, b er øvre integrasjonsgrense. | Der f(x) er integranden, a er nedre integrasjonsgrense, b er øvre integrasjonsgrense. | ||
Dersom det finnes en deriverbar funksjon F(x) er | Dersom det finnes en deriverbar funksjon F(x) er | ||
F'(x) = f(x) | F'(x) = f(x) | ||
$\int f(x)dx = F(x) + C$ | |||
Der C er en konstant. Vi sier at F(x) er en antiderivert av f(x). | |||
Det bestemte integralet blir da: | Det bestemte integralet blir da: | ||
$\int\limits_a^b f(x)dx = F(b)- F(a)$ | |||
Der a og b er integrasjonsgrensene. | Der a og b er integrasjonsgrensene. | ||
| Linje 91: | Linje 94: | ||
Altså forsvinner C. | Altså forsvinner C. | ||
La oss se på | |||
[[File:int-fasit.png]] | |||
Det eksakte svaret på oppgaven er altså: | |||
$\int\limits_1^2 0,3x^2 dx = [\frac{0,3}{3}x^3]_1^2 = 0,1(8-1)= 0,7$ | |||
Tilnærmingen med 50 rektangler (A2 og B2) var altså god. | |||
==3.1.5== | |||
La oss se på eksemplene i begynnelsen: | |||
f(t) = 4 gir: | f(t) = 4 gir: | ||
$\int\limits_0^7 4dt = [4t]_0^7 = 28 -0 = 28 $ | |||
Som var det samme resultatet vi fikk ved å telle ruter. | |||
g(t) = 6 -t gir: | g(t) = 6 -t gir: | ||
$\int\limits_0^5 (6-t)dt = [6t- \frac 12t^2]_0^5 = 30- 12,5 - 0 = 17,5$ | |||
Resultatet tilsvarer det vi fikk ved å telle ruter. | |||
== 3.1.6. Er integral og areal det samme?== | |||
Så langt har vi sett på arealer avgrenset av x-aksen, a, b og en graf som ligger over x-aksen. Hva når grafen til funksjonen ligger under x-aksen? | Så langt har vi sett på arealer avgrenset av x-aksen, a, b og en graf som ligger over x-aksen. Hva når grafen til funksjonen ligger under x-aksen? | ||
La oss finne det bestemte integralet avgrenset av x = -2, x = -1, x-aksen og funksjonen f(x)= | La oss finne det bestemte integralet avgrenset av x = -2, x = -1, x-aksen og funksjonen $f(x)= \frac 1x$ | ||
[[File:int en over x.png]] | |||
Geogebra gir oss et integral på - 0,69, Altså en negativ verdi. Regning for hånd gir: | |||
$\int\limits_{-2}^{-1} \frac 1x dx dx = ln |-1| - ln |-2| = 0 - 0,69 = -0,69$ | |||
Man ser at dette stemmer med grafen til ln (x), som er tegnet lilla i samme koordinatsystem. | |||
| Linje 111: | Linje 142: | ||
Et eksempel til: | Et eksempel til: | ||
f(x) = sin x | |||
$\int\limits_0^{2\pi} (sinx) dx = [-cos x]_0^{2\pi} = -1 -(-1)= 0 $ | |||
| Linje 118: | Linje 152: | ||
Fra disse eksemplene ser vi at integralet og arealet IKKE er det samme, selv om vi kan tolke integralet geometrisk. | Fra disse eksemplene ser vi at integralet og arealet IKKE er det samme, selv om vi kan tolke integralet geometrisk. | ||
| Linje 124: | Linje 157: | ||
Noen ganger kan det være vanskelig eller umulig å finne et utrykk for den antideriverte. Da kan man ta utgangspunkt i Riemannsummen og løse problemet numerisk. | Noen ganger kan det være vanskelig eller umulig å finne et utrykk for den antideriverte. Da kan man ta utgangspunkt i Riemannsummen og løse problemet numerisk. | ||
Eller man kan gjøre som en professor jeg kjente. Han brukte saks, papir og en nøyaktig vekt. Ved å klippe ut arealet under grafen | Eller man kan gjøre som en professor jeg kjente. Han brukte saks, tykt papir og en nøyaktig vekt. Ved å klippe ut arealet under grafen og sammenligne det med et kjent areal, ved veiing, kom han fram til tilnærminger gode nok for de fleste ingeniørformål. | ||
Siste sideversjon per 3. sep. 2016 kl. 14:14
3.1.1
Formålet med denne siden er at de som har behovet skal få en viss forståelse for hva integrasjon og integraler er. Du må vite hva derivasjon er først. Dersom du ønsker en mer systematisk og matematisk behandling av emnet går du til integrasjon
3.1.2
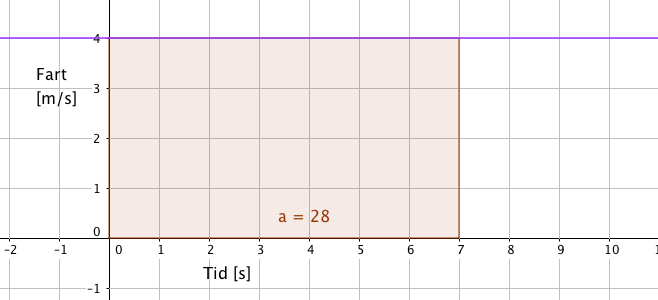
En moped beveger seg med konstant fart 4 meter per sekund. Grafisk kan det se slik ut:
Den fiolette linjen representerer grafen til funksjonen
f(t) = 4.
Vi er interessert i å se på arealet under grafen. Hva forteller det oss?
- Mopeden kjører med konstant hastighet 4m/s i 7 sekunder.
I den perioden tilbakelegger den en strekning S på $S =v\cdot t = 4m/s \cdot 7s = 28m$.
Dersom vi teller antall ruter under grafen, eller regner ut arealet av rektangelet får vi også 28.
- Arealet under grafen til funksjonen som utrykker hastighet som funksjon av tiden gir oss altså tilbakelagt strekning i samme tidsrom.
Legg merke til følgende:
- Når vi skal tolke arealet under en graf er enheten for svaret alltid lik enheten på x- aksen multiplisert med enheten på y-aksen.
I eksemplet over gir det $s \cdot \frac ms = m$
3.1.3
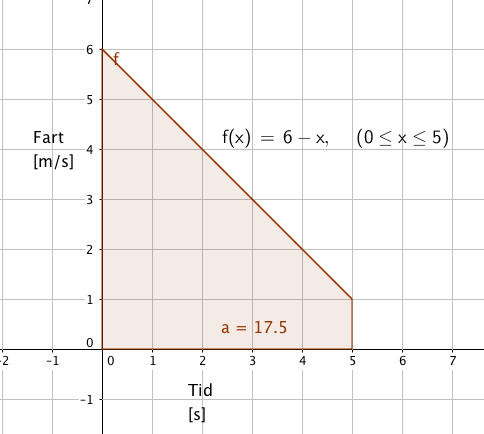
En annen moped kjører med hastigheten 6 meter per sekund og begynner så å bremse opp. Mopeden bremser med en jevn akselerasjon (negativ) fra 6m/s til 1 m/s. Funksjonen som beskriver situasjonen ser slik ut:
g(t) = 6 - t
Dette skjer i løpet av fem sekunder.
I dette eksemplet ser vi at arealet under grafen er 17,5 og at benevningen er m (meter), hvilket betyr at mopeden beveger seg 17,5 meter under oppbremsingen.
De to eksemplene over var med rette linjer, altså lineære funksjoner. Hva da når grafen krummer?
3.1.4
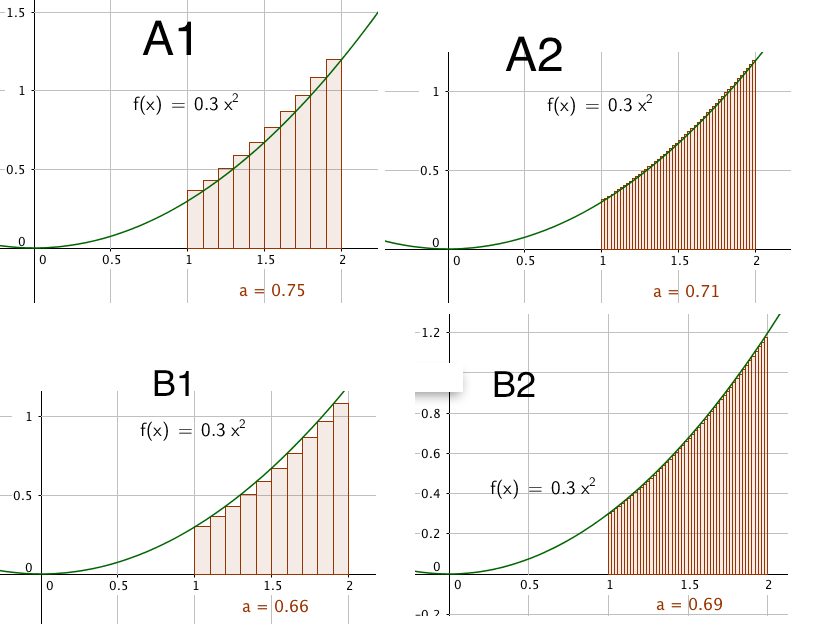
For å finne arealet under krumme kurver kan vi dele området opp i rektangler som vist under
Vi observerer følgende:
- Rektanglene under kurven i figur A1 og A2 vil gi et større areal enn det som faktisk er under kurven.
- Rektanglene under kurven i figur B1 og B2 vil gi et mindre areal enn det som faktisk er under kurven.
- Bredden av rektanglene og derved også antall rektangler, har betydning for nøyaktigheten i resultatet. Både modell A og B vil bevege seg mot arealet under kurven, når antall rektangler går mot uendelig, og bredden av rektanglene avtar. Arealet under kurven er summen av disse rektanglene. Bredden av et rektangel er gitt ved:
$\Delta x = \frac{b-a}{n}$
Der n er antall rektangler, b er øvre grense og a er nedre grense som begrenser arealet under kurven.
Summen $S_n$ av rektanglene under grafen blir:
$S_n = f(x_1)\cdot \Delta x + f(x_2) \cdot \Delta x+..+f(x_n) \cdot \Delta x$ (kalles Riemannsum)
Det bestemte integralet til f er:
$\int\limits_a^b f(x)dx = \lim_{n \to \infty}S_n$
Der f(x) er integranden, a er nedre integrasjonsgrense, b er øvre integrasjonsgrense.
Dersom det finnes en deriverbar funksjon F(x) er
F'(x) = f(x)
$\int f(x)dx = F(x) + C$
Der C er en konstant. Vi sier at F(x) er en antiderivert av f(x).
Det bestemte integralet blir da:
$\int\limits_a^b f(x)dx = F(b)- F(a)$
Der a og b er integrasjonsgrensene.
Du lurer kanskje på hva som skjedde med C? Dersom vi ser på høyre side av likhetstegnet ser vi at
F(b) + C - (F(a) + C) = F(b) - F(a)
Altså forsvinner C.
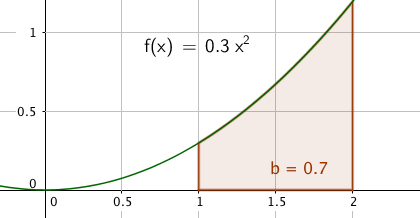
Det eksakte svaret på oppgaven er altså:
$\int\limits_1^2 0,3x^2 dx = [\frac{0,3}{3}x^3]_1^2 = 0,1(8-1)= 0,7$
Tilnærmingen med 50 rektangler (A2 og B2) var altså god.
3.1.5
La oss se på eksemplene i begynnelsen:
f(t) = 4 gir:
$\int\limits_0^7 4dt = [4t]_0^7 = 28 -0 = 28 $
Som var det samme resultatet vi fikk ved å telle ruter.
g(t) = 6 -t gir:
$\int\limits_0^5 (6-t)dt = [6t- \frac 12t^2]_0^5 = 30- 12,5 - 0 = 17,5$
Resultatet tilsvarer det vi fikk ved å telle ruter.
3.1.6. Er integral og areal det samme?
Så langt har vi sett på arealer avgrenset av x-aksen, a, b og en graf som ligger over x-aksen. Hva når grafen til funksjonen ligger under x-aksen?
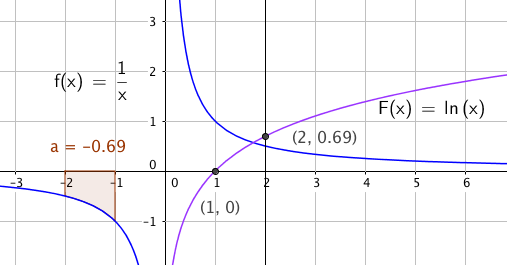
La oss finne det bestemte integralet avgrenset av x = -2, x = -1, x-aksen og funksjonen $f(x)= \frac 1x$
Geogebra gir oss et integral på - 0,69, Altså en negativ verdi. Regning for hånd gir:
$\int\limits_{-2}^{-1} \frac 1x dx dx = ln |-1| - ln |-2| = 0 - 0,69 = -0,69$
Man ser at dette stemmer med grafen til ln (x), som er tegnet lilla i samme koordinatsystem.
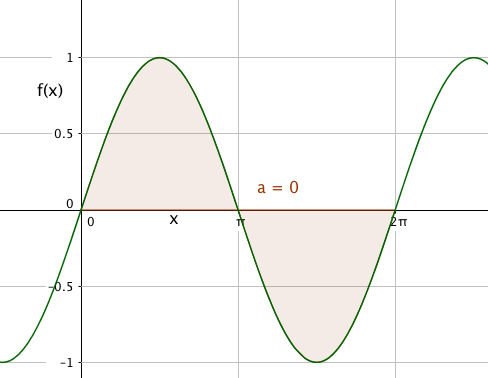
Et eksempel til:
f(x) = sin x
$\int\limits_0^{2\pi} (sinx) dx = [-cos x]_0^{2\pi} = -1 -(-1)= 0 $
Fra disse eksemplene ser vi at integralet og arealet IKKE er det samme, selv om vi kan tolke integralet geometrisk.
Noen ganger kan det være vanskelig eller umulig å finne et utrykk for den antideriverte. Da kan man ta utgangspunkt i Riemannsummen og løse problemet numerisk.
Eller man kan gjøre som en professor jeg kjente. Han brukte saks, tykt papir og en nøyaktig vekt. Ved å klippe ut arealet under grafen og sammenligne det med et kjent areal, ved veiing, kom han fram til tilnærminger gode nok for de fleste ingeniørformål.