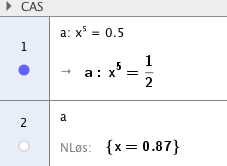2P 2016 vår LØSNING: Forskjell mellom sideversjoner
| (78 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 11: | Linje 11: | ||
==Oppgave 1)== | ==Oppgave 1)== | ||
Temperaturene i stigende rekkefølge | |||
-6, -4, 0, 2, 2, 6. | -6, -4, 0, 2, 2, 6. | ||
| Linje 24: | Linje 26: | ||
Gjennomsnitt: $\frac{-6 +(-4)+0+2+2+6}{6} = \frac 06 =0$ | Gjennomsnitt: $\frac{-6 +(-4)+0+2+2+6}{6} = \frac 06 =0$ | ||
Gjennomsnittstemperaturen denne perioden er null grader celsius. | |||
==Oppgave 2)== | ==Oppgave 2)== | ||
| Linje 30: | Linje 32: | ||
Forutsetter at en måned er 30 dager. | Forutsetter at en måned er 30 dager. | ||
$ | $7\:500\: 000\: 000 \cdot 2 \cdot 30 = \\ 7,5 \cdot 10^9 \cdot 6,0 \cdot 10 = \\7,5 \cdot 6,0 \cdot 10^{10} = \\ 45 \cdot 10^{10} = 4,5 \cdot 10^{11}$ | ||
==Oppgave 3)== | ==Oppgave 3)== | ||
Pris bukse i butikk A: 150 kr, og i butikk B: 120 kr. | |||
===a)=== | ===a)=== | ||
| Linje 60: | Linje 62: | ||
===a)=== | ===a)=== | ||
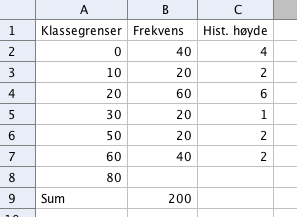
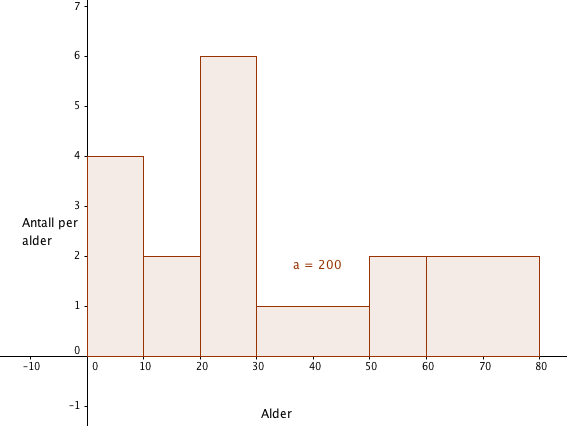
For å finn histogramhøyden tar man frekvens delt på klassebredde, for hver enkelt klasse. | |||
[[File:2p-v16-1-5a1.png]] | |||
[[File:2p-v16-1-5a2.png]] | |||
===b)=== | ===b)=== | ||
Gjennomsnitt i klassedelt materiale: vi antar at elementene i klassen (personer) fordeler seg jevnt utover i klassen. Kan da bruke klassemiddpunkt (alder) og multiplisere med frekvens. | |||
{| width="auto" | |||
| Klasse | |||
|klassemidtpunkt - m | |||
|frekvens - f | |||
| m * f | |||
|- | |||
|[0,10> | |||
|5 | |||
|40 | |||
|200 | |||
|- | |||
|[10, 20> | |||
|15 | |||
|20 | |||
|300 | |||
|- | |||
|[20, 30> | |||
|25 | |||
|60 | |||
|1500 | |||
|- | |||
|[30, 50> | |||
|40 | |||
|20 | |||
|800 | |||
|- | |||
|[50, 60> | |||
|55 | |||
|20 | |||
|1100 | |||
|- | |||
|[60, 80> | |||
|70 | |||
|40 | |||
|2800 | |||
|} | |||
For å finne gjennomsnittet tar man summen av alle produktene m*f og deler på antall personer, som er 200. | |||
$\frac{\sum(m \cdot f)}{200} = \frac{200 + 300 +1500 + 800 + 1100 + 2800}{200} = \frac{6700}{200}= 33,5$ | |||
Gjennomsnittsalderen på beboerne i blokka er ca 33,5 år. | |||
===c)=== | ===c)=== | ||
Medianalderen er gjennomsnittet av person nr. 100 og 101, når det er rangert i stigende rekkefølge. Disse personene befinner seg i klassen 20 - 30 år. I denne klassen er det 6 personer på hvert årstrinn hvilket betyr at medianalderen er ca. 27 år. Aurora er ca. fem år eldre enn medianalderen, men kan jo trøste seg med at hun er yngre enn gjennomsnittet. | |||
==Oppgave 6)== | ==Oppgave 6)== | ||
| Linje 87: | Linje 143: | ||
Fra grafen i a ser man at hun må selge 10 produkter. | Fra grafen i a ser man at hun må selge 10 produkter. | ||
Matematisk kan vi løse det slik: | |||
$370 = 25x + 120 \\ 370 - 120 = 25x \\ 250 = 25x \\ 10 = x $ | |||
==Oppgave 7)== | ==Oppgave 7)== | ||
| Linje 94: | Linje 154: | ||
===a)=== | ===a)=== | ||
Dersom noe øker eksponentielt betyr det at det vokser med en fast prosent hver tidsperiode. | Dersom noe øker eksponentielt betyr det at det vokser med en fast prosent hver tidsperiode. Det kan sees ved at det vokser mer og mer for større x. | ||
===b)=== | ===b)=== | ||
b er eneste kurve som | b er eneste kurve som oppfyller kravet i a. c vokser lineært, altså med en fast størrelse hver tidsperiode. a vokser mindre etter en stund, noe som kan minne om logistisk vekst (ikke pensum i 2P). | ||
==Oppgave 8)== | ==Oppgave 8)== | ||
| Linje 104: | Linje 164: | ||
Skriver alle tallene på standardform: | Skriver alle tallene på standardform: | ||
$ 0,046\cdot 10^{11}= 4,6 \cdot 10^{9} \\ \frac{46}{ | $ 0,046\cdot 10^{11}= 4,6 \cdot 10^{9} \\ \frac{46}{1\ 000\ 000}= 0,000046 = 4,6 \cdot 10^{-5} \\ 46\cdot 10^{-7} =4,6 \cdot 10^{-6} \\ 4\ 600\ 000 = 4,6 \cdot 10^6 \\ 4,6 \cdot 10^8 \\ 0,46\cdot 10^{-6 } = 4,6 \cdot 10^{-7} $ | ||
| Linje 112: | Linje 172: | ||
==Oppgave 9)== | ==Oppgave 9)== | ||
Vi ser at kumulativ frekvens er 20 - altså 20 elever totalt. | |||
Kumulativ frekvens for 6-11 er 15, det betyr at frekvensen må være 10. Relativ frekvens er frekvensen delt på 20. "Nøster" vi opp slik får man følgende tabell: | |||
{| width="auto" | |||
| Antall land | |||
|Frekvens | |||
|Relativ frekvens | |||
| Kumulativ frekvens | |||
|- | |||
|[1,6> | |||
|5 | |||
|0,25 | |||
|5 | |||
|- | |||
|[6, 11> | |||
|10 | |||
|0,5 | |||
|15 | |||
|- | |||
|[11, 16> | |||
|2 | |||
|0,1 | |||
|17 | |||
|- | |||
|[16, 21> | |||
|2 | |||
|0,1 | |||
|19 | |||
|- | |||
|[21, 26> | |||
|1 | |||
|0,05 | |||
|20 | |||
|} | |||
=DEL TO= | =DEL TO= | ||
| Linje 117: | Linje 213: | ||
==Oppgave 1== | ==Oppgave 1== | ||
[[File:2p-v16-2-1.png]] | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 123: | Linje 221: | ||
===a)=== | ===a)=== | ||
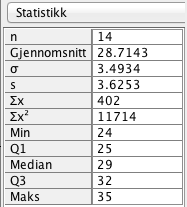
Bruker dataanalyseverktøyet i Geogebra og får: | |||
[[File:2p-v16-2-2a.png]] | |||
gjennomsnittet er 28,7 minutter og standardavviket er 3,6. | |||
===b)=== | ===b)=== | ||
Grete har et jevnere tempo på turene sine. Et lavt standardavvik forteller at det er liten sprik i måleverdiene. | |||
==Oppgave 3== | ==Oppgave 3== | ||
| Linje 130: | Linje 237: | ||
===a)=== | ===a)=== | ||
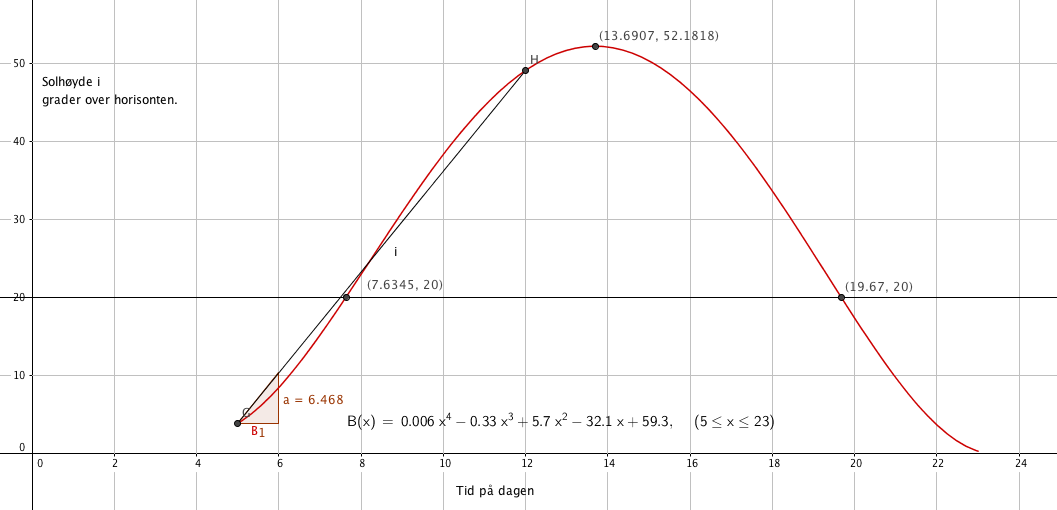
[[File:2p-v16-2-3a.png]] | |||
===b)=== | ===b)=== | ||
Den stod 52,2 grader over horisonten 13,69 timer etter midnatt, altså kl. 13:41. Se figur i a. (Har regnet om fra desimal tid). | |||
===c)=== | ===c)=== | ||
Solen stod 20 grader over horisonten 7,63 og 19,67 timer etter midnatt, altså kl. 07:38 og klokken 19:40. | |||
===d)=== | |||
Solen stiger i gjennomsnitt med ca. 6,5 grader per time i perioden 05:00 til 12:00. | |||
Dette kan også løses ved å bruke «linje» og ikke «linjestykke mellom to punkt» og lese av stigningstallet fra funksjonsuttrykket. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
{| width="auto" | |||
| Figur | |||
|Ant. hvite rektangler | |||
|ant. blå rektangler | |||
|Ant. rektangler totalt | |||
|- | |||
| 1 | |||
|1 | |||
|8 | |||
|9 | |||
|- | |||
|2 | |||
|4 | |||
|12 | |||
|16 | |||
|- | |||
|3 | |||
|9 | |||
|16 | |||
|25 | |||
|- | |||
|4 | |||
|16 | |||
|20 | |||
|36 | |||
|- | |||
|n | |||
| $n^2$ | |||
|$4n + 4$ | |||
|$n^2+4n+4$ | |||
|} | |||
Hvite: her ser vi med en gang fra tabellen og figurene at det er kvadrattall, $n^2$. | |||
Blå: her kan vi regne ut på to måter: | |||
Kun de blå: $4(n+1) = 4n + 4$ | |||
Totalt antall rektangler minus hvite rektangler: | |||
$(n+2)^2 - n^2 = n^2 + 4n + 4 - n^2 = 4n + 4$ | |||
Alle (som nevnt): $(n+2)^2 = n^2+4n + 4$ | |||
===b)=== | |||
Legg merke til at $81 = 9^2$. Fra formelen for totalt antall rektangler ser vi at $9 = (n+2)$ som vil si at $n=7$. Vi trenger derfor $n^2 = 7^2 = 49$ hvite rektangler. | |||
===c)=== | |||
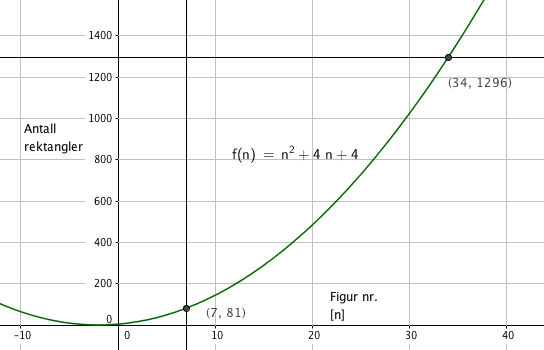
[[File:2p-v16-2-4c.png]] | |||
Skriver inn formelen for totalt antall rektangler som funksjon i Geogebra og finner at det er snakk om figur nr. 34 (ved å skrive y=1296 og finne skjæring med grafen). Antall blå rektangler blir da $4 \cdot 34 + 4= 140$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
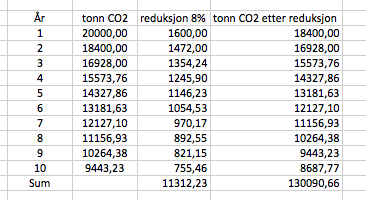
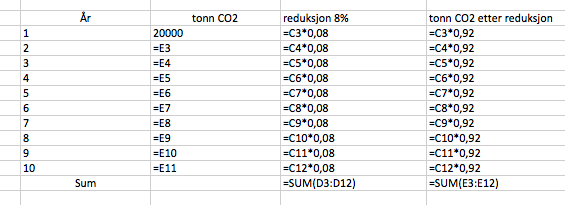
[[File:2p-v16-2-5a1.png]] | |||
[[File:2p-v16-2-5a2.png]] | |||
===b)=== | |||
Bedriften har redusert utslippene med $20 \: 000 - 8\: 687,77 = 11\: 312,23$ tonn | |||
$\frac{11\: 312,23 \cdot 100}{20\: 000}$ = 56,7% | |||
Reduksjonen var på 56,7% over 10 år. | |||
===c)=== | |||
Løser likningen i CAS: | |||
[[File:2p-v16-2-5c.png]] | |||
En vekstfaktor på 0,87 tilsvarer en reduksjon på 13% per år. | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
{| width="auto" | |||
| Lengde av hver side | |||
i kvadratene som | |||
klippes bort | |||
|Lengde av eske | |||
|Bredde av eske | |||
|Høyde av eske | |||
|Volum av eske | |||
|- | |||
| 4 cm | |||
|$20cm - 2\cdot 4cm = 12 cm$ | |||
|$14cm - 2 \cdot 4 cm = 6 cm$ | |||
|4cm | |||
| $288cm^3$ | |||
|- | |||
| 3 cm | |||
|$20cm - 2\cdot 3cm = 14 cm$ | |||
|$14cm - 2 \cdot 4 cm = 8 cm$ | |||
|3cm | |||
| $336cm^3$ | |||
|- | |||
| 2,5 cm | |||
|$20cm - 2\cdot 2,5cm = 15 cm$ | |||
|$14cm - 2 \cdot 2,5 cm = 9 cm$ | |||
|2,5 cm | |||
| $337,5cm^3$ | |||
|- | |||
| x cm | |||
|$20cm - 2\cdot x $ | |||
|$14cm - 2 \cdot x$ | |||
|x | |||
| $4x^3-68x^2+280x$ | |||
|} | |||
===b)=== | |||
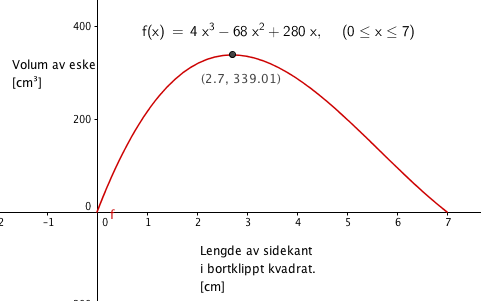
[[File:2p-v16-2-6b.png]] | |||
Esken får sitt største volum når sidekantene i kvadratene som klippes bort er 2,7 cm. Volumet er da 339 $cm^3$. | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
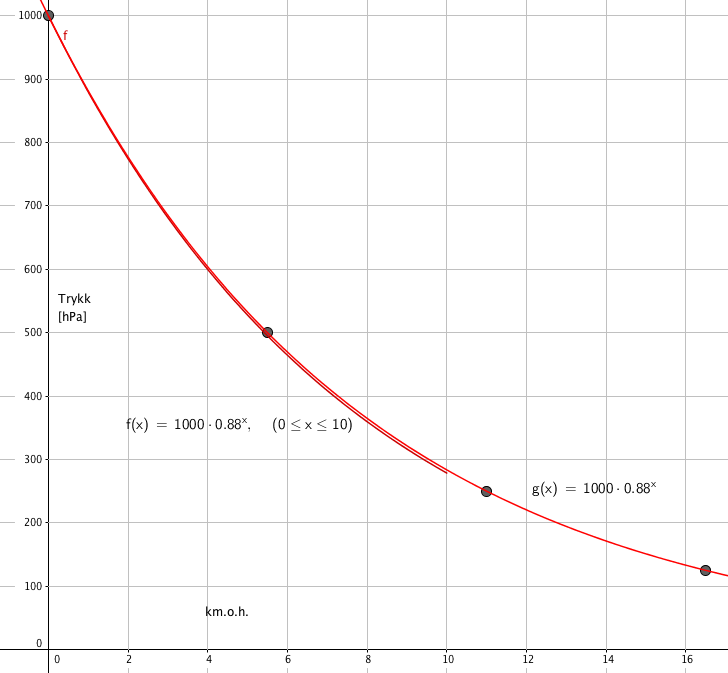
Siden trykket avtar med en fast prosent per km er dette eksponentiell vekst (om enn negativ) med vekstfaktor 1 - 0,12 = 0,88. Dersom vi i tillegg til sitat 1 inkluderer informasjonen om lufttrykket ved havets overflate kan vi sette opp modellen: | |||
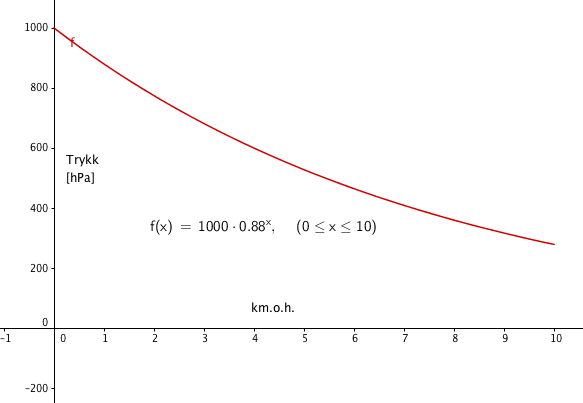
$f(x) = 1000 \cdot 0,88^x$ | |||
Der x er kilometer over havets overflate. | |||
[[File:2p-v16-2-7a.png]] | |||
===b)=== | |||
Lufttrykket halveres for hver 5,5 km opp fra havoverflaten | |||
[[File:2p-v16-2-7b.png]] | |||
Vi observerer at den eksponentielle tilpasningen gir en modell praktisk talt lik den i a. | |||
===c)=== | |||
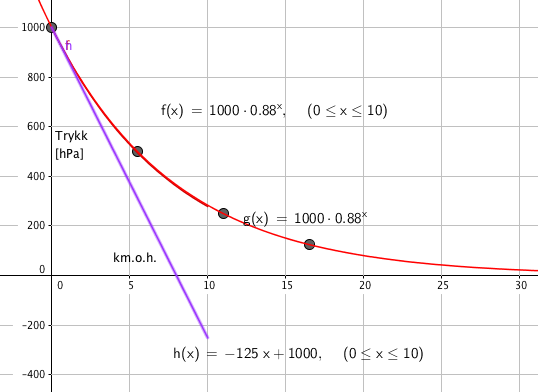
Dette er en lineær modell som trolig virker bra til en hvis høyde over havet. Store høyder gir trolig store feil. | |||
For å finne hvor mye trykket avtar per 1000 meter tar vi 1000:8 = 125 (hPa) | |||
h(x)= -125x + 1000 | |||
[[File:2p-v16-2-7c.png]] | |||
Som vi antok er denne modellen kun gyldig i et lite begrenset område rett over havflaten. | |||
===d)=== | |||
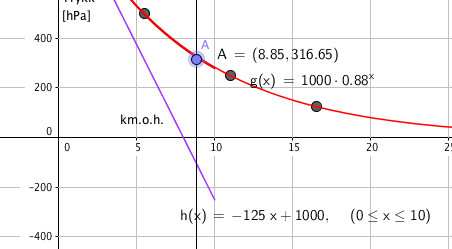
[[File:2p-v16-2-7d.png]] | |||
Modell h er ubrukelig fordi høyden over havet er stor, den gir et negativt trykk?? | |||
Modell f og g er i praksis like og gir et rimelig svar, 317 hPa. Dersom sitat 4 skal tolkes som en absolutt sannhet underestimerer begge modellene marginalt. Man burde da fått 333,33 hPa. | |||
Siste sideversjon per 22. nov. 2017 kl. 18:57
Diskusjon av denne oppgaven på matteprat
Del 1 Løsningsforslag laget av mattepratbruker jøgge
Del 2 Løsningsforslag laget av mattepratbruker jøgge
Løsningsforslag fra mattepratbruker Oyan
DEL EN
Oppgave 1)
Temperaturene i stigende rekkefølge
-6, -4, 0, 2, 2, 6.
Variasjonsbredde: 6 - ( - 6 ) = 12
Variasjonsbredden er 12 grader.
Median: $\frac {0+2}{2} = 1$
Median er 1 grad.
Gjennomsnitt: $\frac{-6 +(-4)+0+2+2+6}{6} = \frac 06 =0$
Gjennomsnittstemperaturen denne perioden er null grader celsius.
Oppgave 2)
Forutsetter at en måned er 30 dager.
$7\:500\: 000\: 000 \cdot 2 \cdot 30 = \\ 7,5 \cdot 10^9 \cdot 6,0 \cdot 10 = \\7,5 \cdot 6,0 \cdot 10^{10} = \\ 45 \cdot 10^{10} = 4,5 \cdot 10^{11}$
Oppgave 3)
Pris bukse i butikk A: 150 kr, og i butikk B: 120 kr.
a)
$\frac{150-120}{120} = \frac 14 = 25$%
Buksene er 25% dyrere i butikk A, i forhold til i butikk B.
b)
$\frac{150-120}{150} = \frac 15 = 20$%
Buksene er 20% billigere i butikk B, i forhold til i butikk A.
Oppgave 4)
Pris på jakke uten MVA:
$x \cdot 1,25 = 750 \\ x= \frac{750}{1,25} = 600$
Jakken koster 600 kroner uten MVA, altså er merverdiavgiften 150 kroner.
Oppgave 5)
a)
For å finn histogramhøyden tar man frekvens delt på klassebredde, for hver enkelt klasse.
b)
Gjennomsnitt i klassedelt materiale: vi antar at elementene i klassen (personer) fordeler seg jevnt utover i klassen. Kan da bruke klassemiddpunkt (alder) og multiplisere med frekvens.
| Klasse | klassemidtpunkt - m | frekvens - f | m * f |
| [0,10> | 5 | 40 | 200 |
| [10, 20> | 15 | 20 | 300 |
| [20, 30> | 25 | 60 | 1500 |
| [30, 50> | 40 | 20 | 800 |
| [50, 60> | 55 | 20 | 1100 |
| [60, 80> | 70 | 40 | 2800 |
For å finne gjennomsnittet tar man summen av alle produktene m*f og deler på antall personer, som er 200.
$\frac{\sum(m \cdot f)}{200} = \frac{200 + 300 +1500 + 800 + 1100 + 2800}{200} = \frac{6700}{200}= 33,5$
Gjennomsnittsalderen på beboerne i blokka er ca 33,5 år.
c)
Medianalderen er gjennomsnittet av person nr. 100 og 101, når det er rangert i stigende rekkefølge. Disse personene befinner seg i klassen 20 - 30 år. I denne klassen er det 6 personer på hvert årstrinn hvilket betyr at medianalderen er ca. 27 år. Aurora er ca. fem år eldre enn medianalderen, men kan jo trøste seg med at hun er yngre enn gjennomsnittet.
Oppgave 6)
a)
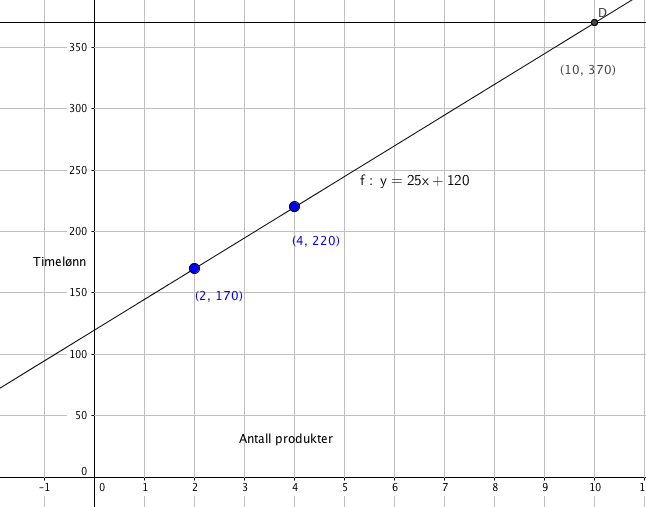
Vi plotter punktene i et koordinatsystem og trekker en rett linje. Denne linjen skjærer y aksen i 120, og stiger med 25 for hver enhet mot høyre på x-aksen.
y-aksen er timelønn og x-aksen er antall enheter.
b)
Den rette linjen i a har uttrykket y = 25x + 120.
Det betyr at fastlønna er 120 kroner og at hun i tillegg tjener 25 kroner for hvert produkt hun selger.
c)
Fra grafen i a ser man at hun må selge 10 produkter.
Matematisk kan vi løse det slik:
$370 = 25x + 120 \\ 370 - 120 = 25x \\ 250 = 25x \\ 10 = x $
Oppgave 7)
a)
Dersom noe øker eksponentielt betyr det at det vokser med en fast prosent hver tidsperiode. Det kan sees ved at det vokser mer og mer for større x.
b)
b er eneste kurve som oppfyller kravet i a. c vokser lineært, altså med en fast størrelse hver tidsperiode. a vokser mindre etter en stund, noe som kan minne om logistisk vekst (ikke pensum i 2P).
Oppgave 8)
Skriver alle tallene på standardform:
$ 0,046\cdot 10^{11}= 4,6 \cdot 10^{9} \\ \frac{46}{1\ 000\ 000}= 0,000046 = 4,6 \cdot 10^{-5} \\ 46\cdot 10^{-7} =4,6 \cdot 10^{-6} \\ 4\ 600\ 000 = 4,6 \cdot 10^6 \\ 4,6 \cdot 10^8 \\ 0,46\cdot 10^{-6 } = 4,6 \cdot 10^{-7} $
Faktoren 4,6 går igjen i alle tallene og vi kan sortere etter størrelse ved å se på eksponenten i tierpotensen:
I stigende rekkefølge: $10^{-7}, 10^{-6}, 10^{-5}, 10^6, 10^8, 10^9.$
Oppgave 9)
Vi ser at kumulativ frekvens er 20 - altså 20 elever totalt.
Kumulativ frekvens for 6-11 er 15, det betyr at frekvensen må være 10. Relativ frekvens er frekvensen delt på 20. "Nøster" vi opp slik får man følgende tabell:
| Antall land | Frekvens | Relativ frekvens | Kumulativ frekvens |
| [1,6> | 5 | 0,25 | 5 |
| [6, 11> | 10 | 0,5 | 15 |
| [11, 16> | 2 | 0,1 | 17 |
| [16, 21> | 2 | 0,1 | 19 |
| [21, 26> | 1 | 0,05 | 20 |
DEL TO
Oppgave 1
Oppgave 2
a)
Bruker dataanalyseverktøyet i Geogebra og får:
gjennomsnittet er 28,7 minutter og standardavviket er 3,6.
b)
Grete har et jevnere tempo på turene sine. Et lavt standardavvik forteller at det er liten sprik i måleverdiene.
Oppgave 3
a)
b)
Den stod 52,2 grader over horisonten 13,69 timer etter midnatt, altså kl. 13:41. Se figur i a. (Har regnet om fra desimal tid).
c)
Solen stod 20 grader over horisonten 7,63 og 19,67 timer etter midnatt, altså kl. 07:38 og klokken 19:40.
d)
Solen stiger i gjennomsnitt med ca. 6,5 grader per time i perioden 05:00 til 12:00.
Dette kan også løses ved å bruke «linje» og ikke «linjestykke mellom to punkt» og lese av stigningstallet fra funksjonsuttrykket.
Oppgave 4
a)
| Figur | Ant. hvite rektangler | ant. blå rektangler | Ant. rektangler totalt |
| 1 | 1 | 8 | 9 |
| 2 | 4 | 12 | 16 |
| 3 | 9 | 16 | 25 |
| 4 | 16 | 20 | 36 |
| n | $n^2$ | $4n + 4$ | $n^2+4n+4$ |
Hvite: her ser vi med en gang fra tabellen og figurene at det er kvadrattall, $n^2$.
Blå: her kan vi regne ut på to måter:
Kun de blå: $4(n+1) = 4n + 4$
Totalt antall rektangler minus hvite rektangler:
$(n+2)^2 - n^2 = n^2 + 4n + 4 - n^2 = 4n + 4$
Alle (som nevnt): $(n+2)^2 = n^2+4n + 4$
b)
Legg merke til at $81 = 9^2$. Fra formelen for totalt antall rektangler ser vi at $9 = (n+2)$ som vil si at $n=7$. Vi trenger derfor $n^2 = 7^2 = 49$ hvite rektangler.
c)
Skriver inn formelen for totalt antall rektangler som funksjon i Geogebra og finner at det er snakk om figur nr. 34 (ved å skrive y=1296 og finne skjæring med grafen). Antall blå rektangler blir da $4 \cdot 34 + 4= 140$
Oppgave 5
a)
b)
Bedriften har redusert utslippene med $20 \: 000 - 8\: 687,77 = 11\: 312,23$ tonn
$\frac{11\: 312,23 \cdot 100}{20\: 000}$ = 56,7%
Reduksjonen var på 56,7% over 10 år.
c)
Løser likningen i CAS:
En vekstfaktor på 0,87 tilsvarer en reduksjon på 13% per år.
Oppgave 6
a)
| Lengde av hver side
i kvadratene som klippes bort |
Lengde av eske | Bredde av eske | Høyde av eske | Volum av eske |
| 4 cm | $20cm - 2\cdot 4cm = 12 cm$ | $14cm - 2 \cdot 4 cm = 6 cm$ | 4cm | $288cm^3$ |
| 3 cm | $20cm - 2\cdot 3cm = 14 cm$ | $14cm - 2 \cdot 4 cm = 8 cm$ | 3cm | $336cm^3$ |
| 2,5 cm | $20cm - 2\cdot 2,5cm = 15 cm$ | $14cm - 2 \cdot 2,5 cm = 9 cm$ | 2,5 cm | $337,5cm^3$ |
| x cm | $20cm - 2\cdot x $ | $14cm - 2 \cdot x$ | x | $4x^3-68x^2+280x$ |
b)
Esken får sitt største volum når sidekantene i kvadratene som klippes bort er 2,7 cm. Volumet er da 339 $cm^3$.
Oppgave 7
a)
Siden trykket avtar med en fast prosent per km er dette eksponentiell vekst (om enn negativ) med vekstfaktor 1 - 0,12 = 0,88. Dersom vi i tillegg til sitat 1 inkluderer informasjonen om lufttrykket ved havets overflate kan vi sette opp modellen:
$f(x) = 1000 \cdot 0,88^x$
Der x er kilometer over havets overflate.
b)
Lufttrykket halveres for hver 5,5 km opp fra havoverflaten
Vi observerer at den eksponentielle tilpasningen gir en modell praktisk talt lik den i a.
c)
Dette er en lineær modell som trolig virker bra til en hvis høyde over havet. Store høyder gir trolig store feil.
For å finne hvor mye trykket avtar per 1000 meter tar vi 1000:8 = 125 (hPa)
h(x)= -125x + 1000
Som vi antok er denne modellen kun gyldig i et lite begrenset område rett over havflaten.
d)
Modell h er ubrukelig fordi høyden over havet er stor, den gir et negativt trykk??
Modell f og g er i praksis like og gir et rimelig svar, 317 hPa. Dersom sitat 4 skal tolkes som en absolutt sannhet underestimerer begge modellene marginalt. Man burde da fått 333,33 hPa.