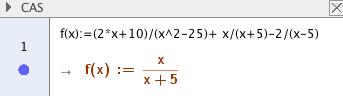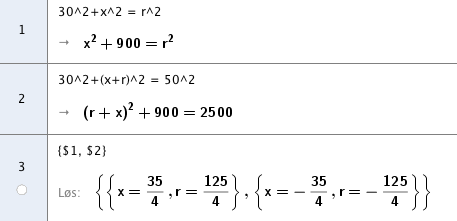R1 eksempeloppgave 2015 vår LØSNING: Forskjell mellom sideversjoner
| (76 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 29: | Linje 29: | ||
$f(x)$ kan da skrives som $(x+3)(x-1)(x-5)$ , hvor alle ledd er av første grad. | $f(x)$ kan da skrives som $(x+3)(x-1)(x-5)$ , hvor alle ledd er av første grad. | ||
Må så tegne et fortegnsskjema for å finne ut når f(x) er mindre eller lik null: | |||
[[File:r1-eksemp2015-12b.png]] | |||
$x \in < \leftarrow, -3] \cup [1,5]$ | |||
==Oppgave 3== | ==Oppgave 3== | ||
Vi har en hypergeometrisk situasjon: | |||
$\frac{\binom{7}{2} \binom{5}{1}}{\binom{12}{3}} = \\ \frac {7 \cdot 3 \cdot 5}{4 \cdot 11 \cdot 5} = \\ \frac {21}{44}$ | |||
Det er 21/44 sannsynlig at det blir to jenter og en gutt i gruppa. | |||
==Oppgave 4== | ==Oppgave 4== | ||
$\frac{x+2}{x^2-16} + \frac {x}{x+4} - \frac{2}{x-4} =\\ \frac{x+2+x(x-4)-2(x+4)}{ ((x+4)(x-4)} =\\ \frac{x+2+x^2-4x-2x-8}{(x+4)(x-4)} = \\ \frac{x^2-5x-6}{(x+4)(x-4)} = \\ \frac{(x+1) (x-6)}{(x+4)(x-4)}$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | ===a)=== | ||
$\frac{a^2(b^2)^2}{a^{-3}b^0} = \\ \frac{a^2b^4}{a^{-3}}= \\ a^{2+3}b^4 = \\ a^5b^4$ | |||
===b)=== | ===b)=== | ||
$lg(a^2 b)+ lg(ab^2)+lg (\frac{a}{b^3}) = \\ 2lg a +lg b + lg a + 2 lgb +lg a - 3lg b = \\ 4 lg a$ | |||
==Oppgave 6== | ==Oppgave 6== | ||
$2^3+2^3+2^3+2^3 = 2^n \\ 4 \cdot 2^3 = 2^n \\ 2^2 \cdot 2^3 = 2^n \\ 2^5 = 2^n \\ n=5$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
$x^2+5x+6=0 \\ (x+2)(x+3)= 0$ | |||
Likningen har løsninger for x=-2 eller for x=-3. Implikasjonspilen må derfor gå fra høyre mot venstre. Altså, x= -2 impliserer løsning. Siden -3 også er en løsning kan ikke implikasjonen gå andre veien, og vi har ikke ekvivalens. | |||
==Oppgave 8== | ==Oppgave 8== | ||
===a)=== | ===a)=== | ||
$\vec{AB} = [3-1, 4-0] = [2,4] \\ \vec{AC} =[2-1, t-0]= [1,t]$ | |||
===b)=== | ===b)=== | ||
$\vec{AB} \cdot \vec{AC} =0 \\ [2,4] \cdot [1,t] = 0 \\ 2+4t =0 \\ t = - \frac 12$ | |||
===c)=== | ===c)=== | ||
$[2,4] =k [1,t] \\ k=2 \wedge 4 = kt$ | |||
Det gir t = 2. | |||
==Oppgave 9== | ==Oppgave 9== | ||
| Linje 63: | Linje 99: | ||
Ekstremalpunkt: | Ekstremalpunkt: | ||
$f´(x)= 0 \\3x^2 - 6x=0 \\3x(x- | $f´(x)= 0 \\3x^2 - 6x=0 \\3x(x-2)=0$ | ||
Det ser ut som om funksjonen kan ha ekstremalpunkter for x=0 og x=2, men vi må sjekke fortegnet for den deriverte på begge sider av x. Om vi ikke får fortegnsskifte er det et terrassepunkt, og ikke et ekstremalpunkt. | |||
f´(-1) = 9 og f´(1) = -3, det betyr at x = 0 gir et maksimumspunkt. f´(4) = 24, igjen har vi fortegnsskifte. Det betyr at funksjonen har et minimumspunkt for x = 2. | |||
Maksimum: (0,0) | |||
Minimum: (2, -4) | |||
===b)=== | ===b)=== | ||
[[File:r1-eks2015-19b.png]] | |||
===c)=== | ===c)=== | ||
Vi dobbelderiverer for å finne vendepunkt: | |||
$f´´(x)= 6x-6 \\ f´´(x) =0 \\ x=1$ | |||
f(1) = - 2 | |||
Funksjonen har et vendepunkt i (1,-2). Tangenten i dette punktet er parallell med funksjonen akkurat i punktet. Selv om den skjærer gjennom grafen til funksjonen kalles den for en vendetangent. f´(1) = -3, det betyr at stigningstallet til tangenten er -3. Likningen for denne er: | |||
$y= ax + b \\ -2 = -3 \cdot 1+ b \\ b= 1 \\ y = -3x + 1$ | |||
==Oppgave 10== | ==Oppgave 10== | ||
===a)=== | ===a)=== | ||
Trekanten ABE er | Trekanten ABE er identisk med trekanten ECD. Begge har en vinkel på 90 grader. Summen av de to andre er 90 grader. Det betyr at vinkel BEA og vinkel CED tilsammen er 90 grader. Derfor er vinkel AED 90 grader. | ||
===b)=== | ===b)=== | ||
Arealer trekanter: | |||
$\triangle ABE = \frac{ab}{2} \\ \triangle DCE = \frac{ab}{2} \\ \triangle AED = \frac{c^2}{2}$ | |||
Arealet av trapeset er: | |||
$A_t = \frac{a+b}{2} (a+b)$ | |||
===c)=== | ===c)=== | ||
Vi setter arealet av trapeset lik arealet av de tre trekantene og får: | |||
$\frac{a+b}{2} (a+b)= \frac {ab}{2} + \frac{ab}{2} + \frac{c^2}{2} \\ (a+b)(a+b)= c^2 + 2ab \\ a^2 + 2ab + b^2 = c^2 + 2ab \\ a^2 + b^2 = c^2$ | |||
(Lurer på om dagens presidentkandidater fikser det like bra :-)) | |||
==Oppgave 11== | ==Oppgave 11== | ||
| Linje 87: | Linje 158: | ||
==Oppgave 12== | ==Oppgave 12== | ||
===a)=== | ===a)=== | ||
CEF er en likebeint trekant. Derfor er EC = CF = $\beta$ | |||
BDE er også en likebeint trekant, derfor er BD = $\alpha$ | |||
Arealet av kvadratet ADSF er $r^2$. Arealet av trekanten DBS er lik arealet av trekanten BES. Arealet av disse to er $\beta \cdot r$. På samme måte er trekantene FSC og CSE like. Samlet areal av de to er $\alpha \cdot r$ | |||
Arealet av ABC: $A_{\triangle ABC} = \alpha r + \beta r + r^2 = (\alpha + \beta)r + r^2$ | |||
===b)=== | ===b)=== | ||
$( \alpha + r)^2 + (\beta + r )^2 = (\alpha + \beta)^2 \\ \alpha^2+ 2 \alpha r + r^2+ \beta ^2+2\beta r + r^2 =\alpha^2+2 \alpha \beta + \beta^2 \\ 2 \alpha r + r^2 + 2\beta r + r^2 = 2 \alpha \beta \\ 2r^2+2r( \alpha + \beta) = 2 \alpha \beta \\ r^2+ r( \alpha + \beta)= \alpha \beta$ | |||
Fra a) : | |||
Arealet av ABC: $A_{\triangle ABC} = \alpha r + \beta r + r^2 = (\alpha + \beta)r + r^2 = \alpha \beta$ | |||
===c)=== | ===c)=== | ||
Areal: $A_{\triangle ABC} = \alpha \beta = 3 \cdot 2 =6$ | |||
Finner r: $r^2 +5r-6 =0$ (fra a og b) | |||
$r= 1$ løsningen r= -6 bortfaller. | |||
==DEL TO== | ==DEL TO== | ||
==Oppgave 1== | ==Oppgave 1== | ||
[[File:r1-eks2015-21b.png]] | |||
[[File:r1-eks2015-21a.png]] | |||
Den opprinnelige funksjonen er ikke definert for x= 5. | |||
Funksjonen er kontinuerlig og deriverbar for $x \in \R \backslash \{ -5, 5 \} $. | |||
==Oppgave 2== | ==Oppgave 2== | ||
[[File:r1-eks2015-22.png]] | |||
Radius er 31,25 | |||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | ===a)=== | ||
Dersom halvparten av jentene går med skjørt er det 20% på skolen som går i skjørt og 80% i bukser. Det ble opplyst at halvparten av jentene gikk i bukser, så : | |||
P(B|J) = 50% | |||
P(B)= 80% | |||
===b)=== | ===b)=== | ||
Sannsynlighet for jente gitt bukser: | |||
P(J|B)= 2/8 = 25% | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | ===a)=== | ||
Areal av drake: A = xy + x(h-y) = hx | |||
Bruker så Pytagoras på to av de ikke kongruente trekantene (kun positive verdier): | |||
$x^2+ y^2 = 25 \\ y= \sqrt {25-x^2}$ | |||
og | |||
$(h-y)^2+ x^2 = 144 \\ h-y= \sqrt{144-x^2}$ | |||
Legger disse sammen og får: | |||
$y + h - y = \sqrt{25-x^2} + \sqrt{144-x^2}$ | |||
Setter inn i uttrykket for A og får: | |||
$A(x)= x( \sqrt{25-x^2} + \sqrt{144-x^2})$ | |||
===b)=== | ===b)=== | ||
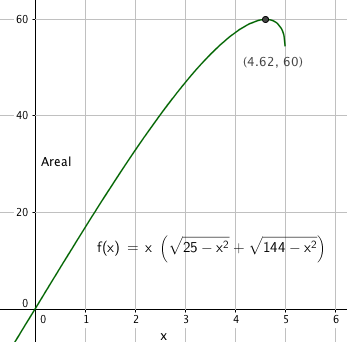
[[File:r1-eksemp2015-24b.png]] | |||
Det største arealet dragen kan ha er $60 dm^2$. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | ===a)=== | ||
Fly B lander når y- koordinaten der null, dvs: $432t^2-72t+3=0$. Det gir løsning for 0,08 timer, eller 4 minutter og 48 sekunder. | |||
===b)=== | ===b)=== | ||
Det er landingstidspunktet. Flyet har da bare fart i x retning. Deriverer posisjonsvektor i x retning og får -204, dvs. 204 km/h mot definert positiv retning. | |||
===c)=== | ===c)=== | ||
Dersom flyene kolliderer må begge være i P på samme tidspunkt. Det betyr at $x_a= x_b \wedge y_a=y_b$, for samme t verdi. | |||
Finner den t verdi som gir samme x koordinat: 70t +2 = -204t + 17 gir t= 0,0547. Det er på dette tidspunkt en høydeforskjell på ca 65 meter, dvs y koordinatene er forskjellige. Om flyene kolliderer vet jeg ikke, men jeg synes marginene her er faretruende små. | |||
==Oppgave 6== | ==Oppgave 6== | ||
[[File:r1-eks-v2015-26.png]] | |||
Avstanden mellom p og q er gitt på linje 7. Vi observerer at denne er dobbelt stor som verdien til r, på linje 6. Altså ligger r midt mellom p og q. | |||
Siste sideversjon per 23. feb. 2016 kl. 09:18
- Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
a)
$f(t)=0.02t^3+0.6t^2+4.1\\f'(t)=0.06t^2+1.2t$
b)
$g(x)=x^2\cdot \ e^{2x}\\g'(x)=2x\cdot \ e^{2x}+x^2\cdot \ 2e^{2x}=2x\cdot \ e^{2x} (1+x)$
c)
$h(x)=ln(x^3+1)\\h'(x)=(ln u)'\cdot \ (x^3+1)' \ = \frac{1}{x^3+1}\cdot \ 3x^2 \ =\frac{3x^2}{x^3+1}$
Opgave 2
a)
$f(x)=x^3+ax^2-13x+15$. Hvis $f(x)$ er delelig med $(x-1)$, er $f(1)=0 \\ $ $1^3+a\cdot \ 1^2-13 \cdot \ 1 +15=0 \\ 1+a+2=0 \\ a=-3$
b)
$ \quad(x^3-3x^2-13x+15):(x-1)=x^2-2x-15\\-(x^3-x^2) \\ \quad \quad -2x^2-13x \\ \quad \quad -(-2x^2+2x) \\ \quad \quad \quad \quad -15x+15 $
Faktoriserer $x^2-2x-15$ ved abc-formelen. Da får vi at $x=5 \vee x=-3$
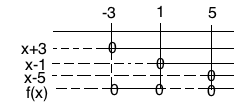
$f(x)$ kan da skrives som $(x+3)(x-1)(x-5)$ , hvor alle ledd er av første grad.
Må så tegne et fortegnsskjema for å finne ut når f(x) er mindre eller lik null:
$x \in < \leftarrow, -3] \cup [1,5]$
Oppgave 3
Vi har en hypergeometrisk situasjon:
$\frac{\binom{7}{2} \binom{5}{1}}{\binom{12}{3}} = \\ \frac {7 \cdot 3 \cdot 5}{4 \cdot 11 \cdot 5} = \\ \frac {21}{44}$
Det er 21/44 sannsynlig at det blir to jenter og en gutt i gruppa.
Oppgave 4
$\frac{x+2}{x^2-16} + \frac {x}{x+4} - \frac{2}{x-4} =\\ \frac{x+2+x(x-4)-2(x+4)}{ ((x+4)(x-4)} =\\ \frac{x+2+x^2-4x-2x-8}{(x+4)(x-4)} = \\ \frac{x^2-5x-6}{(x+4)(x-4)} = \\ \frac{(x+1) (x-6)}{(x+4)(x-4)}$
Oppgave 5
a)
$\frac{a^2(b^2)^2}{a^{-3}b^0} = \\ \frac{a^2b^4}{a^{-3}}= \\ a^{2+3}b^4 = \\ a^5b^4$
b)
$lg(a^2 b)+ lg(ab^2)+lg (\frac{a}{b^3}) = \\ 2lg a +lg b + lg a + 2 lgb +lg a - 3lg b = \\ 4 lg a$
Oppgave 6
$2^3+2^3+2^3+2^3 = 2^n \\ 4 \cdot 2^3 = 2^n \\ 2^2 \cdot 2^3 = 2^n \\ 2^5 = 2^n \\ n=5$
Oppgave 7
$x^2+5x+6=0 \\ (x+2)(x+3)= 0$
Likningen har løsninger for x=-2 eller for x=-3. Implikasjonspilen må derfor gå fra høyre mot venstre. Altså, x= -2 impliserer løsning. Siden -3 også er en løsning kan ikke implikasjonen gå andre veien, og vi har ikke ekvivalens.
Oppgave 8
a)
$\vec{AB} = [3-1, 4-0] = [2,4] \\ \vec{AC} =[2-1, t-0]= [1,t]$
b)
$\vec{AB} \cdot \vec{AC} =0 \\ [2,4] \cdot [1,t] = 0 \\ 2+4t =0 \\ t = - \frac 12$
c)
$[2,4] =k [1,t] \\ k=2 \wedge 4 = kt$
Det gir t = 2.
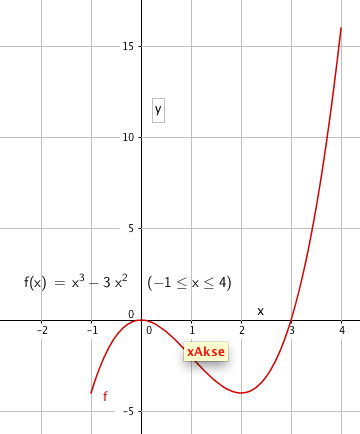
Oppgave 9
a)
Nullpunkt:
$f(x)=0 \\ x^2(x-3) =0 $
Nullpunkt (0, 0) og (3, 0)
Ekstremalpunkt:
$f´(x)= 0 \\3x^2 - 6x=0 \\3x(x-2)=0$
Det ser ut som om funksjonen kan ha ekstremalpunkter for x=0 og x=2, men vi må sjekke fortegnet for den deriverte på begge sider av x. Om vi ikke får fortegnsskifte er det et terrassepunkt, og ikke et ekstremalpunkt.
f´(-1) = 9 og f´(1) = -3, det betyr at x = 0 gir et maksimumspunkt. f´(4) = 24, igjen har vi fortegnsskifte. Det betyr at funksjonen har et minimumspunkt for x = 2.
Maksimum: (0,0)
Minimum: (2, -4)
b)
c)
Vi dobbelderiverer for å finne vendepunkt:
$f´´(x)= 6x-6 \\ f´´(x) =0 \\ x=1$
f(1) = - 2
Funksjonen har et vendepunkt i (1,-2). Tangenten i dette punktet er parallell med funksjonen akkurat i punktet. Selv om den skjærer gjennom grafen til funksjonen kalles den for en vendetangent. f´(1) = -3, det betyr at stigningstallet til tangenten er -3. Likningen for denne er:
$y= ax + b \\ -2 = -3 \cdot 1+ b \\ b= 1 \\ y = -3x + 1$
Oppgave 10
a)
Trekanten ABE er identisk med trekanten ECD. Begge har en vinkel på 90 grader. Summen av de to andre er 90 grader. Det betyr at vinkel BEA og vinkel CED tilsammen er 90 grader. Derfor er vinkel AED 90 grader.
b)
Arealer trekanter:
$\triangle ABE = \frac{ab}{2} \\ \triangle DCE = \frac{ab}{2} \\ \triangle AED = \frac{c^2}{2}$
Arealet av trapeset er:
$A_t = \frac{a+b}{2} (a+b)$
c)
Vi setter arealet av trapeset lik arealet av de tre trekantene og får:
$\frac{a+b}{2} (a+b)= \frac {ab}{2} + \frac{ab}{2} + \frac{c^2}{2} \\ (a+b)(a+b)= c^2 + 2ab \\ a^2 + 2ab + b^2 = c^2 + 2ab \\ a^2 + b^2 = c^2$
(Lurer på om dagens presidentkandidater fikser det like bra :-))
Oppgave 11
$x^2+y^2-4x+6y-12 =0 \\ (x^2-4x+4)+(y^2+6y+9) -12-13 =0 \\(x-2)^2 + (y+3)^2 = 5^2$
Sirkelen har radius 5, med sentrum i (2, -3).
Oppgave 12
a)
CEF er en likebeint trekant. Derfor er EC = CF = $\beta$
BDE er også en likebeint trekant, derfor er BD = $\alpha$
Arealet av kvadratet ADSF er $r^2$. Arealet av trekanten DBS er lik arealet av trekanten BES. Arealet av disse to er $\beta \cdot r$. På samme måte er trekantene FSC og CSE like. Samlet areal av de to er $\alpha \cdot r$
Arealet av ABC: $A_{\triangle ABC} = \alpha r + \beta r + r^2 = (\alpha + \beta)r + r^2$
b)
$( \alpha + r)^2 + (\beta + r )^2 = (\alpha + \beta)^2 \\ \alpha^2+ 2 \alpha r + r^2+ \beta ^2+2\beta r + r^2 =\alpha^2+2 \alpha \beta + \beta^2 \\ 2 \alpha r + r^2 + 2\beta r + r^2 = 2 \alpha \beta \\ 2r^2+2r( \alpha + \beta) = 2 \alpha \beta \\ r^2+ r( \alpha + \beta)= \alpha \beta$
Fra a) :
Arealet av ABC: $A_{\triangle ABC} = \alpha r + \beta r + r^2 = (\alpha + \beta)r + r^2 = \alpha \beta$
c)
Areal: $A_{\triangle ABC} = \alpha \beta = 3 \cdot 2 =6$
Finner r: $r^2 +5r-6 =0$ (fra a og b)
$r= 1$ løsningen r= -6 bortfaller.
DEL TO
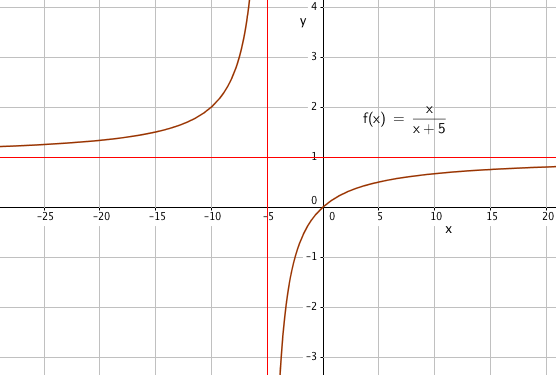
Oppgave 1
Den opprinnelige funksjonen er ikke definert for x= 5.
Funksjonen er kontinuerlig og deriverbar for $x \in \R \backslash \{ -5, 5 \} $.
Oppgave 2
Radius er 31,25
Oppgave 3
a)
Dersom halvparten av jentene går med skjørt er det 20% på skolen som går i skjørt og 80% i bukser. Det ble opplyst at halvparten av jentene gikk i bukser, så :
P(B|J) = 50%
P(B)= 80%
b)
Sannsynlighet for jente gitt bukser:
P(J|B)= 2/8 = 25%
Oppgave 4
a)
Areal av drake: A = xy + x(h-y) = hx
Bruker så Pytagoras på to av de ikke kongruente trekantene (kun positive verdier):
$x^2+ y^2 = 25 \\ y= \sqrt {25-x^2}$
og
$(h-y)^2+ x^2 = 144 \\ h-y= \sqrt{144-x^2}$
Legger disse sammen og får:
$y + h - y = \sqrt{25-x^2} + \sqrt{144-x^2}$
Setter inn i uttrykket for A og får:
$A(x)= x( \sqrt{25-x^2} + \sqrt{144-x^2})$
b)
Det største arealet dragen kan ha er $60 dm^2$.
Oppgave 5
a)
Fly B lander når y- koordinaten der null, dvs: $432t^2-72t+3=0$. Det gir løsning for 0,08 timer, eller 4 minutter og 48 sekunder.
b)
Det er landingstidspunktet. Flyet har da bare fart i x retning. Deriverer posisjonsvektor i x retning og får -204, dvs. 204 km/h mot definert positiv retning.
c)
Dersom flyene kolliderer må begge være i P på samme tidspunkt. Det betyr at $x_a= x_b \wedge y_a=y_b$, for samme t verdi.
Finner den t verdi som gir samme x koordinat: 70t +2 = -204t + 17 gir t= 0,0547. Det er på dette tidspunkt en høydeforskjell på ca 65 meter, dvs y koordinatene er forskjellige. Om flyene kolliderer vet jeg ikke, men jeg synes marginene her er faretruende små.
Oppgave 6
Avstanden mellom p og q er gitt på linje 7. Vi observerer at denne er dobbelt stor som verdien til r, på linje 6. Altså ligger r midt mellom p og q.