R1 2015 vår LØSNING: Forskjell mellom sideversjoner
| (96 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 13: | Linje 13: | ||
[http://www.matematikk.net/res/eksamen/R1/sensur/2015V_Sensorveiledning_REA3022_Matematikk_R1_V2015.pdf Sensorveiledning] | [http://www.matematikk.net/res/eksamen/R1/sensur/2015V_Sensorveiledning_REA3022_Matematikk_R1_V2015.pdf Sensorveiledning] | ||
[http://ndla.no/nb/node/152090?fag=57933 Løsning fra NDLA] | |||
| Linje 34: | Linje 36: | ||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | |||
$P(x)= x^3+2x^2-5x-6 \\ P(2)= 8+8-10-6 =0$ | |||
Altså er polynomet delelig med x - 2. | |||
===b)=== | |||
$ \quad x^3+2x^2-5x-6: (x-2)= x^2+4x+3 \\ -(x^3-2x^2) \\ \quad\quad \quad 4x^2-5x \\ \quad \quad-(4x^2-8x) \\ \quad\quad \quad\quad \quad\quad 3x-6 \\ \quad\quad \quad\quad \quad -(3x-6)$ | |||
Løser $x^2+4x+3=0$ og får | |||
P(x) = ( x - 2)( x + 1)(x + 3) | |||
===c)=== | |||
$lim_{x \rightarrow 2} \frac{(x-2)(x+1)(x+3)}{x-2} = \\ lim_{x \rightarrow 2} (x+1)(x+3) = 15 $ | |||
==Oppgave 3== | ==Oppgave 3== | ||
$\frac{x-2}{x^2+2x} + \frac2x + \frac{x+2}{x^2-2x} - \frac{3x}{x^2 - 4} = \\ \frac{(x-2)(x-2) +2((x+2)(x-2) +(x+2)(x+2) - 3x^2}{x(x+2)(x-2)} = \\ \frac{x^2-4x+4 +2x^2 - 8+ x^2+4x +4-3x^2}{x(x+2)(x-2)} = \\ \frac{x^2}{x(x+2)(x-2)} \\ \frac{x}{(x+2)(x-2)}$ | |||
==Oppgave 4== | ==Oppgave 4== | ||
$x^2-2x +y^2+4y-20=0 \\ (x^2-2x+1) + (y^2+ 4y + 4) - 25 = 0 \\ (x-1)^2 + (y+2)^2 = 5^2$ | |||
Sirkelen har radius 5, med sentrum i punktet (1, -2). | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
$\vec{u} \parallel \vec{v} \Rightarrow \vec u = k \vec v$ | |||
I tillegg må vi skifte fortegn siden den skal være motsatt rettet. Vi multipliserer med -1 og får $ \vec u = [-3, -4]$ | |||
===b)=== | |||
En vektor som står vinkelrett på [a,b] vektor er vektoren k[-b, a]. Vektoren [-4,3] står derfor vinkelrett på [ 3, 4] vektor. Kriteriet er at når to vektorer står vinkelrett på hverandre er skalarproduktet null: | |||
$[3,4]\cdot[-4,3] = -12 +12 = 0$ | |||
===c)=== | |||
$\vec w $ står vinkelrett på $\vec v$ så derfor må t være null. | |||
$\vec v = k \vec u \\ [3,4] = k[-3,-4]$ | |||
I dette tilfellet må k = -1. | |||
===d)=== | |||
Lengde av v vektor: | |||
$ | \vec v | = \sqrt{3^2+4^2} = 5 $ | |||
Dersom lengden av x vektor skal være 7, må v vektoren multipliseres med $\frac 75$: | |||
$ \vec x = \frac 75 \vec v = \frac 75 [3, 4] = [\frac{21}{5}, \frac{28}{5}]$ | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
$\binom {12}{ 2} = \frac{12!}{10! \cdot 2!} = 6 \cdot 11 = 66$ | |||
$\binom {n}{ 1} = \frac{n!}{(n-1)! \cdot 1!} = \frac{n \cdot (n-1) \cdot (n-2)....}{(n-1) \cdot (n-2)....} = n$ | |||
===b)=== | |||
$\frac{\binom{x}{1} \cdot \binom{12-x}{1}}{\binom{12}{2}} = \frac {6}{11} \\ \frac{x \cdot (12-x)}{66 } =\frac{6}{11} \\x(12-x) = 36 \\ x^2-12x+36=0 \\ (x-6)(x-6)=0 \\ x=6 $ | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
$f(x)3xe^{-x} \\ f´(x)= 3e^{-x} -3xe^{-x} = 3e^{-x}(1-x)$ | |||
Funksjonen har et ekstremalpunkt for x=1. For x >1 avtar funksjonen og for x < 1 vokser den. Det betyr at den har et toppunkt for x = 1. $f(1)= \frac 3e$ . | |||
Maksimumspunkt: $(1, \frac 3e )$ | |||
===b)=== | |||
$f(x)3xe^{-x} \\ f´(x)= 3e^{-x} -3xe^{-x} = 3e^{-x}(1-x) \\ f``(x)= -3e^{-x} +3xe^{-x} -3e^{-x}= 3e^{-x}(2-x)$ | |||
===c)=== | |||
[[File:r1-v2015-17c.png]] | |||
==Oppgave 8== | ==Oppgave 8== | ||
===a)=== | |||
Vinkel B er en periferivinkel som spenner over buen AC. Vinkel CSA er en sentralvinkel som spenner over sammen buen. Vinkel DSA er halvparten av vinkel CSA. Vinkel B er derfor lik vinkel DSA. | |||
===b)=== | |||
$\angle B = \angle DSA \\ sinDSA = \frac{\frac 12 b}{R}\\ 2R = \frac{b}{sin B} $ | |||
===c)=== | |||
Tja... Vi gjør det samme med a og c, som vi gjorde med b i oppgave b. Man må lage fotpunkt på BC og AB også. ABS og BCS er også likebeinte så oppgaven er en repetisjon av oppgave b. | |||
==Oppgave 9== | ==Oppgave 9== | ||
$9^x - 3^x -12 = 0 \\ (3^x)^2 - 3^x - 12=0 \\ $ | |||
Setter $u=3^x$ | |||
$u^2-u - 12 =0 \\ u = -3 \vee u = 4$ | |||
Må forkaste u= -3 og får | |||
$3^x = 4 \\ x = \frac{lg 4}{lg3}$ | |||
==DEL TO== | ==DEL TO== | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
[[File:r1-v2015-21ab.png]] | |||
===b)=== | |||
Fra tegningen i a ser man at likningen blir $(x-3)^2 + (y-3)^2 =18$. Altså en sirkel med sentrum i punktet (3, 3) og med radius $\sqrt{18}$ | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | |||
[[File:r1-v2015-22abc.png]] | |||
===b)=== | |||
Fra Figuren i a leser vi at farten må være 12 - 58 km/h. | |||
===c)=== | |||
Det passerer flest biler, ca. 30 stykker per minutt, når farten er ca. 26 km/h. | |||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | |||
V deriverer posisjonsvektoren og får: | |||
$\vec{r_A}(t)= [18t-8,10-3t] \\ \vec v =\vec{r_A}´(t) =[18,-3] $ | |||
og | |||
$\vec{r_B}(t)= [10t, 20-6t] \\ \vec v = \vec{r_B}´(t) =[10,-6] $ | |||
Litt amatørmessig å oppgi farten til båter i km/h, men la gå: | |||
$v_A = \sqrt{18^2+(-3)^2} \approx 18,2$ km/h | |||
og | |||
$v_B = \sqrt{10^2+(-6)^2} \approx 11,6$ km/h | |||
===b)=== | |||
Avstanden mellom båtene vil til enhver tid være en vektor i x-retning pluss en vektor i y- retning. Resultanten blir hypotenusen i en rettvinklet trekant og Pytagoras kan brukes: | |||
$d= \sqrt {| \vec r_A|^2 +|\vec r_B|^2} \\ d= \sqrt{(18t - 8- 10t)^2 + (10-3t - (20-6t))} \\ d= \sqrt{(8t-8)^2+(3t-10)^2}$ | |||
===c)=== | |||
Vi skriver uttrykket for d inn i Geogebra og finner minimumspunktet: | |||
[[File:r1-v2015-23c.png]] | |||
Avstanden er minst etter ca 1 time og 17 minutter, ca 6,55 km. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
f har nullpunkt for x= 1 gir: 1 + a + b + c+ 1 = 0 | |||
x = 2 er x- koordinat til vendepunktet. f''(x) = $12x^2+ 6ax + 2b$. f''(2)=0 gir: 48 + 12a + 2b = 0 | |||
f(3) = 4 gir: 4 = 81 + 27a + 9b + 3c + 1 | |||
===b)=== | |||
[[File:r1-v2015-24b.png]] | |||
a= -6, b = 12, c= -8. Det gir funksjonen: | |||
$f(x)=x^4-6x^3+12x^2-8x +1, \quad D_f =\R$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
$g´(x)= 3ax^2-2x \\ g´(t)= 3at^2-2t$ | |||
Vi har nå funnet stigningstallet til tangenten i P. Finner så b i likningen for den rette linje: | |||
$y = ax+ b\\ at^3-t^2=(3at^2-2t)t + b \\ b= t^2-2at^3$ | |||
Innsatt i y= ax + b gir det: | |||
$y= (3at^2-2t)x + t^2- 2at^3$ | |||
===b)=== | |||
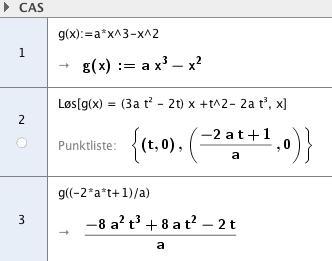
[[File:r1-v2015-25b.png]] | |||
1. Definerer g(x) i CAS. | |||
2. Finner skjæringspunktene mellom g og den rette linje. | |||
3. Finner $g( \frac{-2at+1}{a})$ og finner punktet Q i tredje kvadrant: $( \frac{-2at+1}{a}, \frac{-8a^2t^3+8at^2-2t}{a})$. | |||
Siste sideversjon per 12. mai 2017 kl. 17:14
Diskusjon av denne oppgaven på matteprat
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
a)
$f(x)= x^3+2x^2-3x \\ f´(x)=3x^2+4x-3$
b)
$g(x)= ln(x-2) \\ g´(x)= \frac{1}{x-2}$
c)
$h(x)= (2x^2-1)^3 \\ h´(x) = 3(2x^2-1)^2 \cdot 4x = 12x(2x^2-1)^2$
Oppgave 2
a)
$P(x)= x^3+2x^2-5x-6 \\ P(2)= 8+8-10-6 =0$
Altså er polynomet delelig med x - 2.
b)
$ \quad x^3+2x^2-5x-6: (x-2)= x^2+4x+3 \\ -(x^3-2x^2) \\ \quad\quad \quad 4x^2-5x \\ \quad \quad-(4x^2-8x) \\ \quad\quad \quad\quad \quad\quad 3x-6 \\ \quad\quad \quad\quad \quad -(3x-6)$
Løser $x^2+4x+3=0$ og får
P(x) = ( x - 2)( x + 1)(x + 3)
c)
$lim_{x \rightarrow 2} \frac{(x-2)(x+1)(x+3)}{x-2} = \\ lim_{x \rightarrow 2} (x+1)(x+3) = 15 $
Oppgave 3
$\frac{x-2}{x^2+2x} + \frac2x + \frac{x+2}{x^2-2x} - \frac{3x}{x^2 - 4} = \\ \frac{(x-2)(x-2) +2((x+2)(x-2) +(x+2)(x+2) - 3x^2}{x(x+2)(x-2)} = \\ \frac{x^2-4x+4 +2x^2 - 8+ x^2+4x +4-3x^2}{x(x+2)(x-2)} = \\ \frac{x^2}{x(x+2)(x-2)} \\ \frac{x}{(x+2)(x-2)}$
Oppgave 4
$x^2-2x +y^2+4y-20=0 \\ (x^2-2x+1) + (y^2+ 4y + 4) - 25 = 0 \\ (x-1)^2 + (y+2)^2 = 5^2$
Sirkelen har radius 5, med sentrum i punktet (1, -2).
Oppgave 5
a)
$\vec{u} \parallel \vec{v} \Rightarrow \vec u = k \vec v$
I tillegg må vi skifte fortegn siden den skal være motsatt rettet. Vi multipliserer med -1 og får $ \vec u = [-3, -4]$
b)
En vektor som står vinkelrett på [a,b] vektor er vektoren k[-b, a]. Vektoren [-4,3] står derfor vinkelrett på [ 3, 4] vektor. Kriteriet er at når to vektorer står vinkelrett på hverandre er skalarproduktet null:
$[3,4]\cdot[-4,3] = -12 +12 = 0$
c)
$\vec w $ står vinkelrett på $\vec v$ så derfor må t være null.
$\vec v = k \vec u \\ [3,4] = k[-3,-4]$
I dette tilfellet må k = -1.
d)
Lengde av v vektor:
$ | \vec v | = \sqrt{3^2+4^2} = 5 $
Dersom lengden av x vektor skal være 7, må v vektoren multipliseres med $\frac 75$:
$ \vec x = \frac 75 \vec v = \frac 75 [3, 4] = [\frac{21}{5}, \frac{28}{5}]$
Oppgave 6
a)
$\binom {12}{ 2} = \frac{12!}{10! \cdot 2!} = 6 \cdot 11 = 66$
$\binom {n}{ 1} = \frac{n!}{(n-1)! \cdot 1!} = \frac{n \cdot (n-1) \cdot (n-2)....}{(n-1) \cdot (n-2)....} = n$
b)
$\frac{\binom{x}{1} \cdot \binom{12-x}{1}}{\binom{12}{2}} = \frac {6}{11} \\ \frac{x \cdot (12-x)}{66 } =\frac{6}{11} \\x(12-x) = 36 \\ x^2-12x+36=0 \\ (x-6)(x-6)=0 \\ x=6 $
Oppgave 7
a)
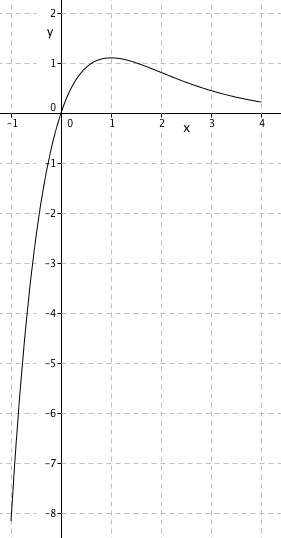
$f(x)3xe^{-x} \\ f´(x)= 3e^{-x} -3xe^{-x} = 3e^{-x}(1-x)$
Funksjonen har et ekstremalpunkt for x=1. For x >1 avtar funksjonen og for x < 1 vokser den. Det betyr at den har et toppunkt for x = 1. $f(1)= \frac 3e$ .
Maksimumspunkt: $(1, \frac 3e )$
b)
$f(x)3xe^{-x} \\ f´(x)= 3e^{-x} -3xe^{-x} = 3e^{-x}(1-x) \\ f``(x)= -3e^{-x} +3xe^{-x} -3e^{-x}= 3e^{-x}(2-x)$
c)
Oppgave 8
a)
Vinkel B er en periferivinkel som spenner over buen AC. Vinkel CSA er en sentralvinkel som spenner over sammen buen. Vinkel DSA er halvparten av vinkel CSA. Vinkel B er derfor lik vinkel DSA.
b)
$\angle B = \angle DSA \\ sinDSA = \frac{\frac 12 b}{R}\\ 2R = \frac{b}{sin B} $
c)
Tja... Vi gjør det samme med a og c, som vi gjorde med b i oppgave b. Man må lage fotpunkt på BC og AB også. ABS og BCS er også likebeinte så oppgaven er en repetisjon av oppgave b.
Oppgave 9
$9^x - 3^x -12 = 0 \\ (3^x)^2 - 3^x - 12=0 \\ $
Setter $u=3^x$
$u^2-u - 12 =0 \\ u = -3 \vee u = 4$
Må forkaste u= -3 og får
$3^x = 4 \\ x = \frac{lg 4}{lg3}$
DEL TO
Oppgave 1
a)
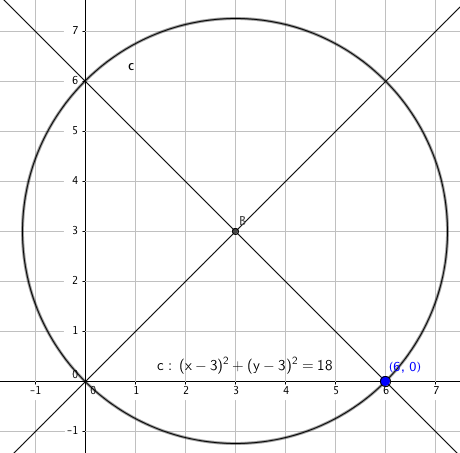
b)
Fra tegningen i a ser man at likningen blir $(x-3)^2 + (y-3)^2 =18$. Altså en sirkel med sentrum i punktet (3, 3) og med radius $\sqrt{18}$
Oppgave 2
a)
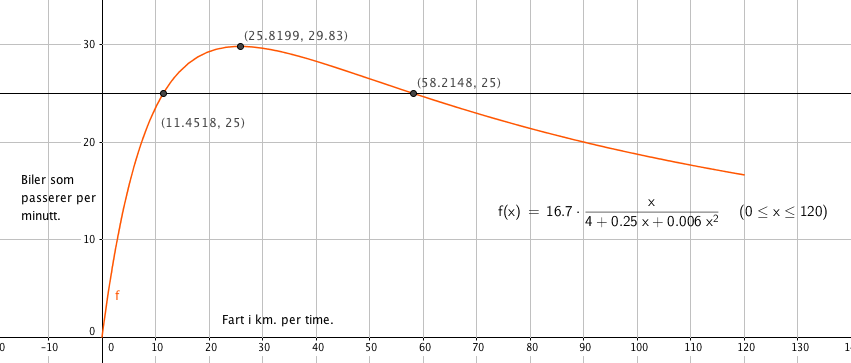
b)
Fra Figuren i a leser vi at farten må være 12 - 58 km/h.
c)
Det passerer flest biler, ca. 30 stykker per minutt, når farten er ca. 26 km/h.
Oppgave 3
a)
V deriverer posisjonsvektoren og får:
$\vec{r_A}(t)= [18t-8,10-3t] \\ \vec v =\vec{r_A}´(t) =[18,-3] $
og
$\vec{r_B}(t)= [10t, 20-6t] \\ \vec v = \vec{r_B}´(t) =[10,-6] $
Litt amatørmessig å oppgi farten til båter i km/h, men la gå:
$v_A = \sqrt{18^2+(-3)^2} \approx 18,2$ km/h
og
$v_B = \sqrt{10^2+(-6)^2} \approx 11,6$ km/h
b)
Avstanden mellom båtene vil til enhver tid være en vektor i x-retning pluss en vektor i y- retning. Resultanten blir hypotenusen i en rettvinklet trekant og Pytagoras kan brukes:
$d= \sqrt {| \vec r_A|^2 +|\vec r_B|^2} \\ d= \sqrt{(18t - 8- 10t)^2 + (10-3t - (20-6t))} \\ d= \sqrt{(8t-8)^2+(3t-10)^2}$
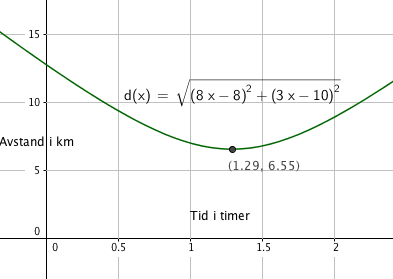
c)
Vi skriver uttrykket for d inn i Geogebra og finner minimumspunktet:
Avstanden er minst etter ca 1 time og 17 minutter, ca 6,55 km.
Oppgave 4
a)
f har nullpunkt for x= 1 gir: 1 + a + b + c+ 1 = 0
x = 2 er x- koordinat til vendepunktet. f(x) = $12x^2+ 6ax + 2b$. f(2)=0 gir: 48 + 12a + 2b = 0
f(3) = 4 gir: 4 = 81 + 27a + 9b + 3c + 1
b)
a= -6, b = 12, c= -8. Det gir funksjonen:
$f(x)=x^4-6x^3+12x^2-8x +1, \quad D_f =\R$
Oppgave 5
a)
$g´(x)= 3ax^2-2x \\ g´(t)= 3at^2-2t$
Vi har nå funnet stigningstallet til tangenten i P. Finner så b i likningen for den rette linje:
$y = ax+ b\\ at^3-t^2=(3at^2-2t)t + b \\ b= t^2-2at^3$
Innsatt i y= ax + b gir det:
$y= (3at^2-2t)x + t^2- 2at^3$
b)
1. Definerer g(x) i CAS.
2. Finner skjæringspunktene mellom g og den rette linje.
3. Finner $g( \frac{-2at+1}{a})$ og finner punktet Q i tredje kvadrant: $( \frac{-2at+1}{a}, \frac{-8a^2t^3+8at^2-2t}{a})$.