1P 2015 høst LØSNING: Forskjell mellom sideversjoner
m →a) |
|||
| (59 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 97: | Linje 97: | ||
===b)=== | ===b)=== | ||
( 186cm + mors høyde) $\cdot$ 0,5 + 7 cm = 189 cm. | |||
$(186 +x) \cdot 0,5 +7 = 189 \\ (186+x) \cdot 0,5 = 182 \\ 186+x = 364 \\x= 178$ | $(186 +x) \cdot 0,5 +7 = 189 \\ (186+x) \cdot 0,5 = 182 \\ 186+x = 364 \\x= 178$ | ||
| Linje 109: | Linje 109: | ||
===a)=== | ===a)=== | ||
Volum av sylinder: $V= \pi r^2 h$ | |||
Ved overslag runder man tallen til noe som blir lettere å regne med, samtidig som man ikke bør fjerne seg for langt fra de eksakte verdiene. Når man ganger sammen to eller flere tall kan det være lurt å runde noen opp og noen ned: | |||
$V= \pi \cdot 0,6^2 \cdot 1,2 \\ \approx 3 \cdot 0,4 \cdot 1,2 \\ = 1,44$ | |||
Alle benevninger var i meter, det betyr at svaret er i kubikkmeter: $1,44m^3 = 1440 dm^3$, som er det samme som 1440 liter. | |||
Volumet til en rundball er i størrelsesorden 1400 liter. (Om du fikk et annet svar kan det være like riktig siden dette kun er et overslag). | |||
===b)=== | ===b)=== | ||
Overflate av sylinder: | |||
$O = 2 \pi r^2 + 2 \pi r h$ | |||
Setter Pi = 3 og får: | |||
$O = 2 \pi r^2 + 2 \pi \cdot r \cdot h \\ O \approx 2 \cdot 3 r^2 + 2 \cdot 3 \cdot r \cdot h \\ O \approx 6 \cdot 0,36 + 6 \cdot 0,6 \cdot 1,2 \\ O \approx 2,16 + 3,6 \cdot 1,2 \\ O \approx 6,48$ | |||
Nøyaktig svar er 6,76, så et sted mellom 7 - 7,5 $m^2$ er helt akseptabelt. Jeg fikk altså 6,48$m^2$. Kanskje du føler behov for å avrunde radius og høyde også? Du kan jo teste litt og se hva slags effekt det har på svaret. | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 116: | Linje 137: | ||
= | {| width="auto" | ||
| | |||
|Smittet | |||
|Ikke smittet | |||
|sum | |||
|- | |||
| Tester positivt | |||
| 58 | |||
|10 | |||
| 68 | |||
|- | |||
|Tester ikke positivt | |||
|2 | |||
|290 | |||
|292 | |||
|- | |||
|sum | |||
|60 | |||
|300 | |||
|360 | |||
|} | |||
===b)=== | ===b)=== | ||
P( pos | smittet) = $\frac{58}{60} = \frac{29}{30}$ | |||
===c)=== | ===c)=== | ||
P( ikke smittet | pos test) = $\frac{10}{68} = \frac{5}{34}$ | |||
==Oppgave 8== | ==Oppgave 8== | ||
$f(x)= -x$ | |||
Dette er en rett linje uten konstantledd, det betyr at grafen går gjennom origo. Den har stigningstall -1, (en til høyre, en ned) hvilket betyr a B er riktig graf. | |||
$g(x) = -x^2+x+2$ | |||
Dette er en parabel eller andregradsfunksjon. Når det står minus foran andregradsleddet betyr det at den vender sin hule side ned. Den skjærer y-aksen i 2. Både graf A og F oppfyller disse kravene. Vi sjekker nullpunktet x = 2 for F: $- (2^2)+2+2 =0$. Graf F tilhører funksjonen g. | |||
$h(x)= \frac 12x + 1$ | |||
En rett linje som skjærer y-aksen i en og stiger med en halv. Graf E passer til funksjon h. | |||
==DEL TO== | ==DEL TO== | ||
| Linje 133: | Linje 190: | ||
===a)=== | ===a)=== | ||
[[File:1p-h2015-21abc.png]] | |||
===b)=== | ===b)=== | ||
Kostnader og inntekter er like store for 20 og 70 enheter, fra figuren i a. | |||
===c)=== | |||
For at overskuddet skal bli størst mulig må det produseres og selges 45 enheter. Overskuddet er da 5312,50 kroner. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 145: | Linje 205: | ||
===a)=== | ===a)=== | ||
Dette er eksponentiell vekst, med vekstfaktor lik 0,85. | |||
$V(2) = 8600 \cdot 0,85^2 = 6213,50$ | |||
Om to år er scooterens verdi ca 6200 kroner, i følge modellen. | |||
===b)=== | ===b)=== | ||
$x \cdot 0,85^3 = 8600 \\ x = 8600 \cdot 0,85^{-3} \\ x= 14003,66$ | |||
Når scooteren var ny kostet den 14 000 kroner. | |||
==Oppgave 3== | ==Oppgave 3== | ||
| Linje 154: | Linje 223: | ||
===a)=== | ===a)=== | ||
Leser av diagram: oljeprisen går fra 85 dollar fatet til ca. 49 dolar fatet. | |||
Det er en nedgang på: $\frac{85-49}{85} = 0,4235 \approx$ 42,4% | |||
===b)=== | ===b)=== | ||
Et fat olje kostet 85 USD. | |||
Prisen på en dollar var ca. 6,60 NOK. | |||
Prisen på et fat olje i NOK blir da: $85 USD \cdot 6,60 NOK/USD = 561 kroner$ | |||
===c)=== | ===c)=== | ||
I begynnelsen av perioden var oljeprisen 561 NOK. | |||
I slutten av perioden er den $49 \cdot 7,7 $ NOK =377,3 NOK. | |||
I prosent tilsvarer det $\frac{561 - 377,3}{561 } \approx$ 32,8% | |||
===d)=== | ===d)=== | ||
Oljeprisen faller. Den er normalt knyttet opp mot $ (USD). Når oljeprisen går ned og dollaren går opp vil fallet i oljepris bli noe kompensert med høy dollarkurs, i forhold til norsk krone. Fallet i oljepris i dollar var 42,4%, men kompensert for sterkere dollar var fallet "bare" 32,8% i norske kroner. Alvorlig nok det. | |||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 166: | Linje 251: | ||
===a)=== | ===a)=== | ||
[[File:1p-h2015-24a1.png]] | |||
Nettolønna er 15 407 kroner i februar. | |||
Formler: | |||
[[File:1p-h2015-24a2.png]] | |||
===b)=== | ===b)=== | ||
[[File:1p-h2015-24b1.png]] | |||
Hun overførte 3325,60 kroner til sparekontoen i februar. | |||
Formler: | |||
[[File:1p-h2015-24b2.png]] | |||
Legg merke til at formelen i celle C22 inneholder en betingelse om at nettolønna ( celle C18) skal være større enn 15000 kroner, hvis ikke settes verdien til null. Dette er nødvendig for ikke å få negativer verdier dersom månedslønna er mindre enn 15000 (det er ikke slik at hun tar ut penger fra sparekontoen dersom netto månedslønn er mindre enn 15000 kroner). | |||
===c)=== | ===c)=== | ||
[[File:1p-h2015-24c.png]] | |||
Her er ett eksempel på situasjonen vi tok høyde for i oppgave b. Bidraget på 60% av det over 15000 kroner er nå null, fordi nettolønna er under 15000 kroner. | |||
Hun vil overføre 2858,20 kroner til sparekontoen. | |||
==Oppgave 5== | ==Oppgave 5== | ||
| Linje 177: | Linje 285: | ||
===a)=== | ===a)=== | ||
AF, bruker Pytagoras: $AF = \sqrt{25-9} = 4$ | |||
Trekant ADF er formlik med trekant ABG. | |||
$\frac{AG}{4} = \frac{9}{3} \\ 2AG = 36 \\ AG = 12 $ | |||
FG = AG - AF = 12 - 4 = 8 | |||
===b)=== | ===b)=== | ||
Det sies ingenting om høyden i kjeglestumpen. Riktig svar er da at volumet ligger mellom null og uendelig antall liter, siden høyden kan være hva som helst... | |||
Men, vi antar at oppgaven har en sammenheng med oppgave a. | |||
Vi finner volumet av tanken ved å finne volumet av kjeglen definert ved ABC, for så å trekke fra volumet av kjeglen definert ved ADE. | |||
$V_{tank} = V_{ABC} - V_{ADE} \\ V_{tank} = \frac 13 \pi (9m)^2 \cdot 12m - \frac 13 \pi (3m)^2 \cdot 4m \\ V_{tank} = (324 \pi - 12 \pi)m^3 = (312 \pi) m^3 \\ V_{tank} \approx 980,2 m^3 = 980200 liter $ | |||
===c)=== | ===c)=== | ||
Vannet renner inn med konstant fart. Etter hvert som vannet stiger blir grunnflaten i kjeglestumpen større. For å fylle et gitt volum blir derfor høyden i kjeglestumpen mindre etter hvert som vannet stiger. Det betyr at vannet stiger saktere og saktere og at graf 3 illustrer dette. | |||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 187: | Linje 312: | ||
===a)=== | ===a)=== | ||
Jeg tolker det slik at det samme sko paret skal brukes tre dager på rad. Vi har parene A, B og C. | |||
Sannsynlighet for å velge par A i tre dager: $\frac 13 \cdot \frac 13 \cdot \frac 13$ | |||
Men, det er tre par å trekke fra, AAA, BBB og CCC, derfor må man multiplisere med 3: | |||
P(samme par tre dager på rad)= $3 \cdot \frac 13 \cdot \frac 13 \cdot \frac 13 = \frac 19 $ | |||
===b)=== | ===b)=== | ||
Første dag kan han velge tre av tre, andre dag to av tre og siste dag en av tre: | |||
P( forskjellige sko hver dag) = $1 \cdot \frac 23 \cdot \frac 13 = \frac 29$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 194: | Linje 330: | ||
===a)=== | ===a)=== | ||
$40 km/h = \frac{40000m}{3600s} =11,1 m/s$ | |||
===b)=== | ===b)=== | ||
Bremselengde sommerføre: | |||
Fart 40 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(11,1 m/s)^2}{19,6 \cdot 0.8} = 7,9 m$ | |||
Fart 80 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(22,2 m/s)^2}{19,6 \cdot 0.8} = 31,5 m$ | |||
Bremselengde vinterføre: | |||
Fart 40 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(11,1 m/s)^2}{19,6 \cdot 0.2} = 31,4 m$ | |||
Fart 80 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(22,2 m/s)^2}{19,6 \cdot 0.2} = 125,7 m$ | |||
===c)=== | ===c)=== | ||
Når farten dobles blir bremselengden tilnærmet firedoblet. Dette gjelder både sommer og vinter. | |||
$\frac{31,5}{7,9} \approx \frac{125,7}{31,4} \approx 4$ | |||
Bremselengde og fart er ikke proporsjonale størrelser. Om de hadde vært det skulle den ene doble seg når den andre dobler seg. | |||
===d)=== | ===d)=== | ||
Fra utregningene i b ser man at farten på vinterstid bør halveres om man ønsker samme bremselengde. | |||
$ v^2 = 19,5\cdot f \cdot s \\ \frac{v^2_{sommer}}{v^2_{vinter}} = \frac{19,6s \cdot 0,8}{19,6s \cdot 0,2} \\ \frac{v_{sommer}}{v_{vinter}} = \sqrt 4 = 2$ | |||
Siste sideversjon per 5. apr. 2017 kl. 07:53
- Diskusjon av denne oppgaven på matteprat
- mer diskusjon av denne oppgaven på matteprat
- Løsningsforslag del 1 av jøgge
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.
DEL EN
Oppgave 1
a)
$\frac {0,4}{1,0} = \frac{2,4}{x} \\ 0,4x = 2,4 \\ x= \frac{2,4}{0,4} \\ x= 6$
Man bør ikke spise mere enn 6 gram salt daglig.
b)
Dersom 100g inneholder 0,8g vil 300g inneholde tre ganger så mye:
$0,8g \cdot 3= 2,4g$ salt
En porsjon pizza inneholder 2,4 gram salt.
c)
$ 2,4 \cdot 0,4g = 0,96 g$ natrium.
$0,96 : 2,4 = \\ 9,6: 24= 0,4$
Dvs 40% av dagsbehovet.
Oppgave 2
a)
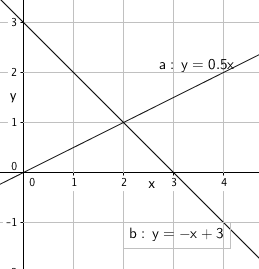
Ved avlesning: skjæringspunkt i (2, 1).
b)
$f(x)= g(x) \\ \frac 12x = -x+3 \\ x =-2x + 6 \\ 3x =6 \\ x=2$
f(2)= 1
Skjæringspunkt mellom f og g : (2,1)
Oppgave 3
Reallønn = nominell lønn $\cdot \frac{100}{ indeks} $
$360000= 450000 \cdot \frac {100}{x} \\ x = \frac{45000000}{360000} =125$
Konsumprisindeksen var på 125 det året.
Oppgave 4
Dersom omvendt proporsjonale størrelser: $y = \frac kx \\ xy=k$
20kr / is $\cdot$ 200 is = 4000 kr
25kr / is $\cdot$ 160 is = 4000 kr
40kr / is $\cdot$ 100 is = 4000 kr
Pris og antall er omvendt proporsjonale størrelser.
Oppgave 5
a)
Gutt: ( fars høyde + mors høyde) $\cdot$ 0,5 + 7 cm
Jente: ( fars høyde + mors høyde) $\cdot$ 0,5 - 7 cm
Ola: ( 180 cm + 160 cm) $\cdot$ 0,5 + 7 cm = 177 cm
Kari: ( 180 cm + 160 cm) $\cdot$ 0,5 - 7 cm = 163 cm
Kari blir 163 cm og Ola 177 cm, i følge formlene.
b)
( 186cm + mors høyde) $\cdot$ 0,5 + 7 cm = 189 cm.
$(186 +x) \cdot 0,5 +7 = 189 \\ (186+x) \cdot 0,5 = 182 \\ 186+x = 364 \\x= 178$
Mor er 178 centimeter høy, i følge formelen.
Oppgave 6
a)
Volum av sylinder: $V= \pi r^2 h$
Ved overslag runder man tallen til noe som blir lettere å regne med, samtidig som man ikke bør fjerne seg for langt fra de eksakte verdiene. Når man ganger sammen to eller flere tall kan det være lurt å runde noen opp og noen ned:
$V= \pi \cdot 0,6^2 \cdot 1,2 \\ \approx 3 \cdot 0,4 \cdot 1,2 \\ = 1,44$
Alle benevninger var i meter, det betyr at svaret er i kubikkmeter: $1,44m^3 = 1440 dm^3$, som er det samme som 1440 liter.
Volumet til en rundball er i størrelsesorden 1400 liter. (Om du fikk et annet svar kan det være like riktig siden dette kun er et overslag).
b)
Overflate av sylinder:
$O = 2 \pi r^2 + 2 \pi r h$
Setter Pi = 3 og får:
$O = 2 \pi r^2 + 2 \pi \cdot r \cdot h \\ O \approx 2 \cdot 3 r^2 + 2 \cdot 3 \cdot r \cdot h \\ O \approx 6 \cdot 0,36 + 6 \cdot 0,6 \cdot 1,2 \\ O \approx 2,16 + 3,6 \cdot 1,2 \\ O \approx 6,48$
Nøyaktig svar er 6,76, så et sted mellom 7 - 7,5 $m^2$ er helt akseptabelt. Jeg fikk altså 6,48$m^2$. Kanskje du føler behov for å avrunde radius og høyde også? Du kan jo teste litt og se hva slags effekt det har på svaret.
Oppgave 7
| Smittet | Ikke smittet | sum | |
| Tester positivt | 58 | 10 | 68 |
| Tester ikke positivt | 2 | 290 | 292 |
| sum | 60 | 300 | 360 |
b)
P( pos | smittet) = $\frac{58}{60} = \frac{29}{30}$
c)
P( ikke smittet | pos test) = $\frac{10}{68} = \frac{5}{34}$
Oppgave 8
$f(x)= -x$
Dette er en rett linje uten konstantledd, det betyr at grafen går gjennom origo. Den har stigningstall -1, (en til høyre, en ned) hvilket betyr a B er riktig graf.
$g(x) = -x^2+x+2$
Dette er en parabel eller andregradsfunksjon. Når det står minus foran andregradsleddet betyr det at den vender sin hule side ned. Den skjærer y-aksen i 2. Både graf A og F oppfyller disse kravene. Vi sjekker nullpunktet x = 2 for F: $- (2^2)+2+2 =0$. Graf F tilhører funksjonen g.
$h(x)= \frac 12x + 1$
En rett linje som skjærer y-aksen i en og stiger med en halv. Graf E passer til funksjon h.
DEL TO
Oppgave 1
a)
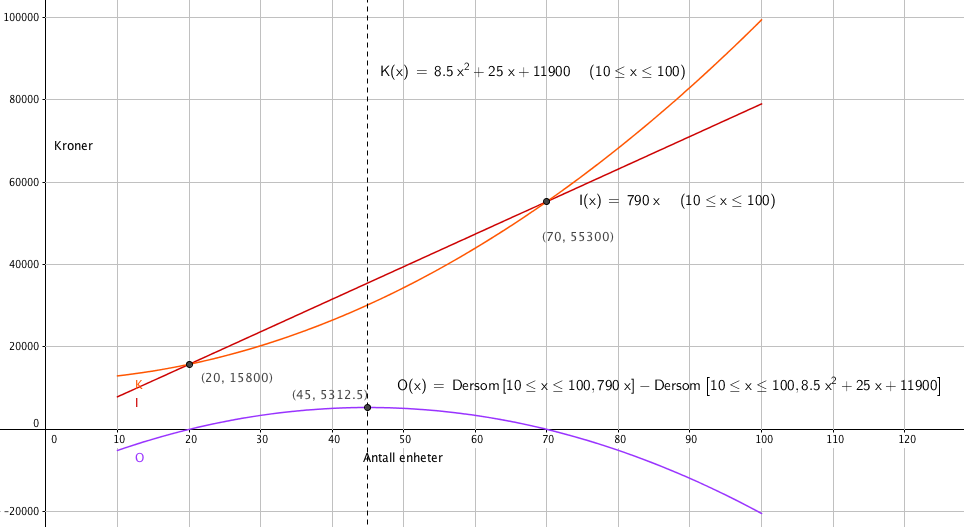
b)
Kostnader og inntekter er like store for 20 og 70 enheter, fra figuren i a.
c)
For at overskuddet skal bli størst mulig må det produseres og selges 45 enheter. Overskuddet er da 5312,50 kroner.
Oppgave 2
a)
Dette er eksponentiell vekst, med vekstfaktor lik 0,85.
$V(2) = 8600 \cdot 0,85^2 = 6213,50$
Om to år er scooterens verdi ca 6200 kroner, i følge modellen.
b)
$x \cdot 0,85^3 = 8600 \\ x = 8600 \cdot 0,85^{-3} \\ x= 14003,66$
Når scooteren var ny kostet den 14 000 kroner.
Oppgave 3
a)
Leser av diagram: oljeprisen går fra 85 dollar fatet til ca. 49 dolar fatet.
Det er en nedgang på: $\frac{85-49}{85} = 0,4235 \approx$ 42,4%
b)
Et fat olje kostet 85 USD.
Prisen på en dollar var ca. 6,60 NOK.
Prisen på et fat olje i NOK blir da: $85 USD \cdot 6,60 NOK/USD = 561 kroner$
c)
I begynnelsen av perioden var oljeprisen 561 NOK.
I slutten av perioden er den $49 \cdot 7,7 $ NOK =377,3 NOK.
I prosent tilsvarer det $\frac{561 - 377,3}{561 } \approx$ 32,8%
d)
Oljeprisen faller. Den er normalt knyttet opp mot $ (USD). Når oljeprisen går ned og dollaren går opp vil fallet i oljepris bli noe kompensert med høy dollarkurs, i forhold til norsk krone. Fallet i oljepris i dollar var 42,4%, men kompensert for sterkere dollar var fallet "bare" 32,8% i norske kroner. Alvorlig nok det.
Oppgave 4
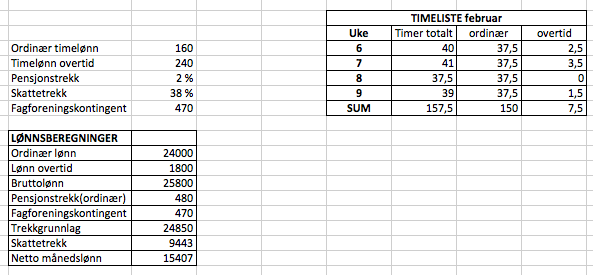
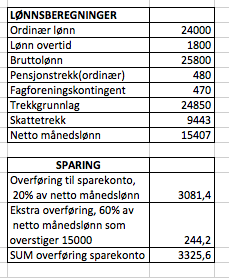
a)
Nettolønna er 15 407 kroner i februar.
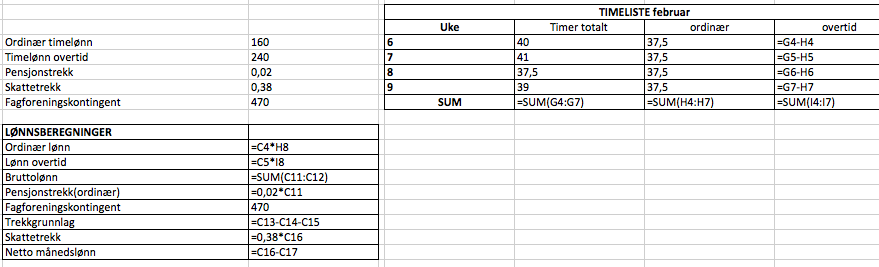
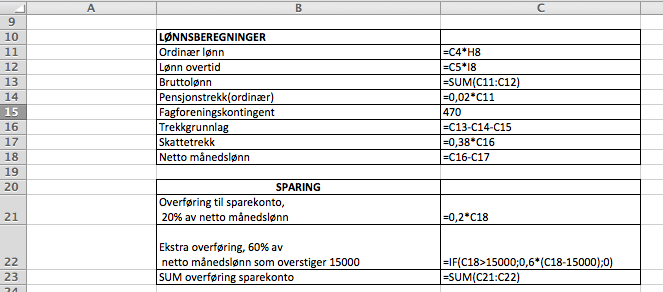
Formler:
b)
Hun overførte 3325,60 kroner til sparekontoen i februar.
Formler:
Legg merke til at formelen i celle C22 inneholder en betingelse om at nettolønna ( celle C18) skal være større enn 15000 kroner, hvis ikke settes verdien til null. Dette er nødvendig for ikke å få negativer verdier dersom månedslønna er mindre enn 15000 (det er ikke slik at hun tar ut penger fra sparekontoen dersom netto månedslønn er mindre enn 15000 kroner).
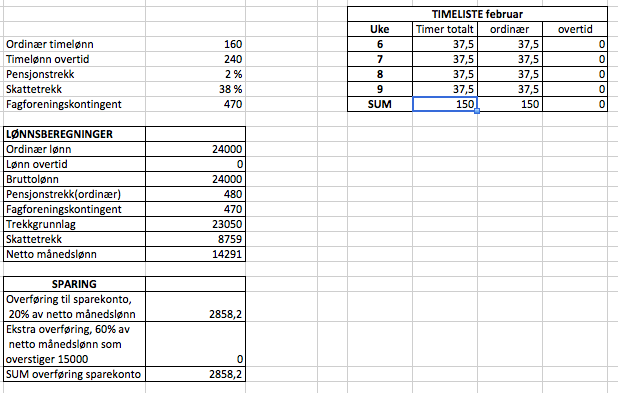
c)
Her er ett eksempel på situasjonen vi tok høyde for i oppgave b. Bidraget på 60% av det over 15000 kroner er nå null, fordi nettolønna er under 15000 kroner.
Hun vil overføre 2858,20 kroner til sparekontoen.
Oppgave 5
a)
AF, bruker Pytagoras: $AF = \sqrt{25-9} = 4$
Trekant ADF er formlik med trekant ABG.
$\frac{AG}{4} = \frac{9}{3} \\ 2AG = 36 \\ AG = 12 $
FG = AG - AF = 12 - 4 = 8
b)
Det sies ingenting om høyden i kjeglestumpen. Riktig svar er da at volumet ligger mellom null og uendelig antall liter, siden høyden kan være hva som helst...
Men, vi antar at oppgaven har en sammenheng med oppgave a.
Vi finner volumet av tanken ved å finne volumet av kjeglen definert ved ABC, for så å trekke fra volumet av kjeglen definert ved ADE.
$V_{tank} = V_{ABC} - V_{ADE} \\ V_{tank} = \frac 13 \pi (9m)^2 \cdot 12m - \frac 13 \pi (3m)^2 \cdot 4m \\ V_{tank} = (324 \pi - 12 \pi)m^3 = (312 \pi) m^3 \\ V_{tank} \approx 980,2 m^3 = 980200 liter $
c)
Vannet renner inn med konstant fart. Etter hvert som vannet stiger blir grunnflaten i kjeglestumpen større. For å fylle et gitt volum blir derfor høyden i kjeglestumpen mindre etter hvert som vannet stiger. Det betyr at vannet stiger saktere og saktere og at graf 3 illustrer dette.
Oppgave 6
a)
Jeg tolker det slik at det samme sko paret skal brukes tre dager på rad. Vi har parene A, B og C.
Sannsynlighet for å velge par A i tre dager: $\frac 13 \cdot \frac 13 \cdot \frac 13$
Men, det er tre par å trekke fra, AAA, BBB og CCC, derfor må man multiplisere med 3:
P(samme par tre dager på rad)= $3 \cdot \frac 13 \cdot \frac 13 \cdot \frac 13 = \frac 19 $
b)
Første dag kan han velge tre av tre, andre dag to av tre og siste dag en av tre:
P( forskjellige sko hver dag) = $1 \cdot \frac 23 \cdot \frac 13 = \frac 29$
Oppgave 7
a)
$40 km/h = \frac{40000m}{3600s} =11,1 m/s$
b)
Bremselengde sommerføre:
Fart 40 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(11,1 m/s)^2}{19,6 \cdot 0.8} = 7,9 m$
Fart 80 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(22,2 m/s)^2}{19,6 \cdot 0.8} = 31,5 m$
Bremselengde vinterføre:
Fart 40 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(11,1 m/s)^2}{19,6 \cdot 0.2} = 31,4 m$
Fart 80 km/h: $s=\frac{v^2}{19,6 \cdot f} = \frac{(22,2 m/s)^2}{19,6 \cdot 0.2} = 125,7 m$
c)
Når farten dobles blir bremselengden tilnærmet firedoblet. Dette gjelder både sommer og vinter.
$\frac{31,5}{7,9} \approx \frac{125,7}{31,4} \approx 4$
Bremselengde og fart er ikke proporsjonale størrelser. Om de hadde vært det skulle den ene doble seg når den andre dobler seg.
d)
Fra utregningene i b ser man at farten på vinterstid bør halveres om man ønsker samme bremselengde.
$ v^2 = 19,5\cdot f \cdot s \\ \frac{v^2_{sommer}}{v^2_{vinter}} = \frac{19,6s \cdot 0,8}{19,6s \cdot 0,2} \\ \frac{v_{sommer}}{v_{vinter}} = \sqrt 4 = 2$