2P 2015 vår LØSNING: Forskjell mellom sideversjoner
| (44 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 14: | Linje 14: | ||
Median av seks målinger er | Median av seks målinger er gjennomsnittet av måling 3 og 4. | ||
Tre tall er allerede under 7, det betyr at tall nr 3 er 6 (fredag). Det betyr at det må være 8 grader på lørdag, dersom median skal bli 7, fordi 8 + 6 = 14, som delt på to er 7. | Tre tall er allerede under 7, det betyr at tall nr 3 er 6 (fredag). Det betyr at det må være 8 grader på lørdag, dersom median skal bli 7, fordi 8 + 6 = 14, som delt på to er 7. | ||
| Linje 70: | Linje 70: | ||
===a)=== | ===a)=== | ||
Gjennomsnitt i klassedelt materiale finner man ved å anta at verdiene i hver klasse fordeler seg jevnt rundt klassemidtpunktet. Vi får da: | |||
$Gj = \frac{25 \cdot 10 + 35 \cdot 20 + 45 \cdot 30 + 60 \cdot 40}{100} = \frac{4700}{100} = 47$ år. | |||
===b)=== | ===b)=== | ||
[[File:2p-v15-6bh.png]] | |||
===c)=== | ===c)=== | ||
| Linje 90: | Linje 95: | ||
|[30, 40> | |[30, 40> | ||
|20 | |20 | ||
| | |$\frac{2}{10}$ | ||
|30 | |30 | ||
|- | |- | ||
|[40,50> | |[40,50> | ||
|30 | |30 | ||
| | |$\frac{3}{10}$ | ||
|60 | |60 | ||
|- | |- | ||
|[ 50,70> | |[ 50,70> | ||
|40 | |40 | ||
| | |$\frac{4}{10}$ | ||
|100 | |100 | ||
|- | |- | ||
| Linje 145: | Linje 150: | ||
[[File:2p-v15-8.png]] | [[File:2p-v15-8.png]] | ||
Han starter 30 km hjemmefra og sykler mot hjemmet med konstant fart. Han kommer nærmere og nærmere og er hjemme etter to og en halv time. | Han starter 30 km hjemmefra og sykler mot hjemmet med konstant fart. Han kommer nærmere og nærmere og er hjemme etter to og en halv time. Funksjonen over viser avstand fra hjemmet f, som funksjon av tiden i timer, x. | ||
==DEL TO== | ==DEL TO== | ||
| Linje 170: | Linje 174: | ||
===b)=== | ===b)=== | ||
Fra stigningstallet i a ser man at økningen per år i gjennomsnitt er ca1480 nye kvinnelige studenter. | |||
===c)=== | ===c)=== | ||
Fra Figuren i a ser man at antall kvinnelige studenter forventes å passere 85000 i 2022, forutsatt at modellen holder så langt ( 9år) inn i fremtiden. | |||
==Oppgave 3 == | ==Oppgave 3 == | ||
| Linje 177: | Linje 185: | ||
===a)=== | ===a)=== | ||
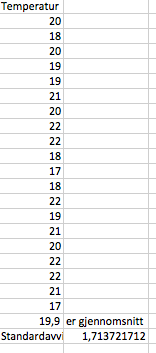
[[File:2p-v15-3a.png]] | |||
Gjennomsnittstemperaturen er 19,9 grader celsius, med et standardavvik på 1,7 grader. | |||
===b)=== | ===b)=== | ||
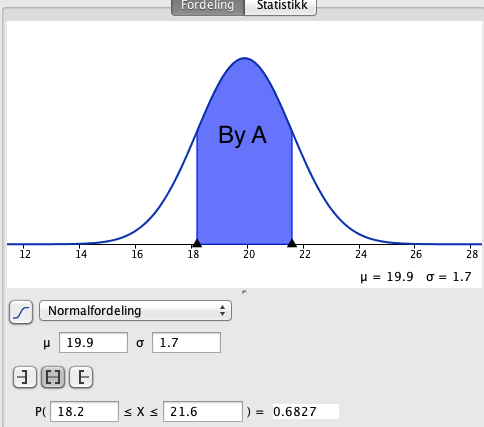
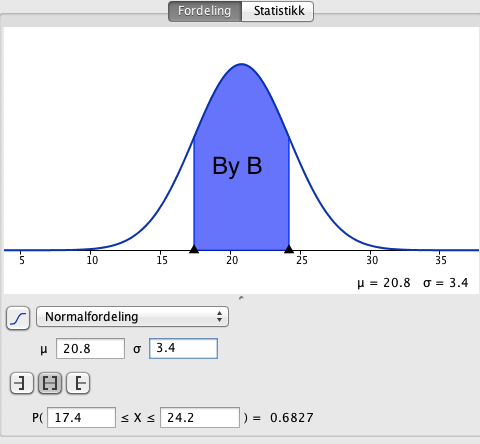
[[File:2p-v15-3b1.png]][[File:2p-v15-3b2.png]] | |||
Gjennomsnittstemperaturen i by B er 0,9 grader høyere enn i by A, men standardavviket for temperaturdata til by B er dobbelt så stor som for by A. Temperaturen i by B er derfor mere usikker enn den i A. Vi observerer at innenfor et standardavvik forskyves nedre temperatugrense i B med 0,8 grader celsius lavere enn i A. | |||
==Oppgave 4== | ==Oppgave 4== | ||
| Linje 185: | Linje 199: | ||
===a)=== | ===a)=== | ||
$F_4$ vil ha fire trekanter mere enn $ F_3$, altså $18+ 4 \cdot 3 = 30 $ linjestykker. | |||
===b)=== | ===b)=== | ||
Figurene består av en eller flere likesida trekanter. Antall linjestykker øker med 3n, fra en figur til den neste. | |||
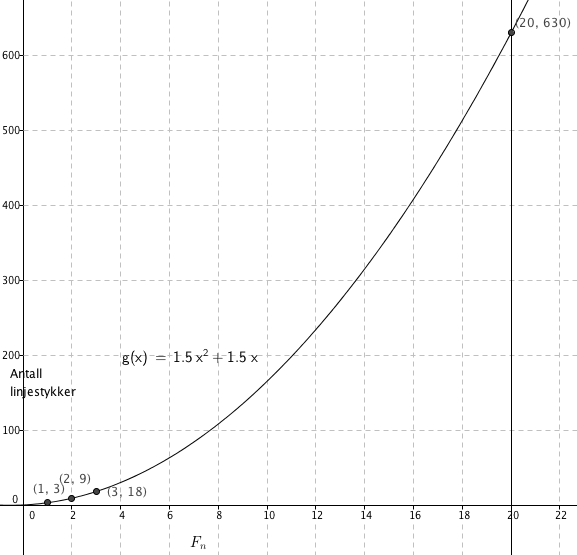
[[File:2p-v15-4b.png]] | |||
Formler: [[File:2p-v15-4b2.png]] og så videre... | |||
===c)=== | ===c)=== | ||
| Linje 199: | Linje 222: | ||
===a)=== | ===a)=== | ||
Erstatning minker med 10% per år, derfor vekstfaktor 0,9. | |||
x er antall år, derfor $0,9^x$ | |||
Erstatningsbeløp når sykkelen er ny er innkjøpspris P, minus egenandel, derfor (P- 2000) | |||
===b)=== | ===b)=== | ||
$F(x)=(P-2000) 0,9^x \\ F(7) = (10000 - 2000)0,9^7 \\ F(7) = 3826,38$ | |||
Da får man utbetalt ca. 3826 kroner. | |||
===c)=== | ===c)=== | ||
$F(x)=(P-2000) 0,9^x -150x$ | |||
Det siste leddet er premiekostnadene, 150x. | |||
===d)=== | ===d)=== | ||
$F(x)=(P-2000) 0,9^x -150x \\F(13)= 8000 \cdot 0,9^{13} -150 \cdot 13 \\ V(13) = 83,50$ | |||
Du får da netto utbetalt 83,50 kroner. Du får egentlig utbetalt i overkant av 2000 kroner, men når man trekker fra det forsikringen har kostet deg sitter du igjen med 83,50. Hva er sannsynligheten for at en 13 år gammel sykkel blir stjålet? Litt avhengig av risikobildet og hvor god sykkellås jeg har ville jeg vurdere å kutte forsikringen etter ca. 5 år. | |||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 223: | Linje 262: | ||
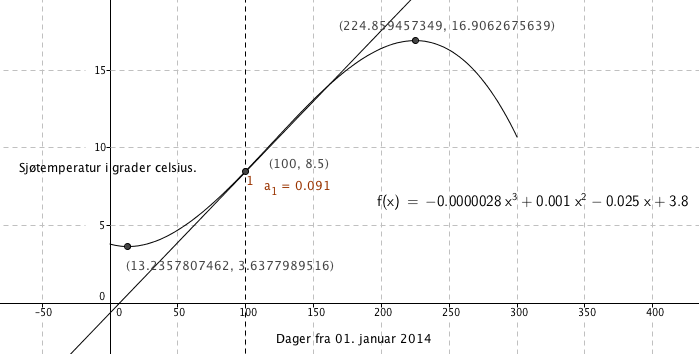
Det forteller at dag 100 i 2014 hadde en vanntemperatur på 8,5 grader, på det aktuelle stedet. | Det forteller at dag 100 i 2014 hadde en vanntemperatur på 8,5 grader, på det aktuelle stedet. | ||
Den momentane | Den momentane veksten er, ut fra figuren 0,091. Det betyr at vanntemperaturen akkurat denne dagen øker med 0,091 grader. Dette er jo på våren så det er jo naturlig. | ||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 229: | Linje 268: | ||
===a)=== | ===a)=== | ||
Grunnflaten av boksen består av et rektangel med areale xy og en sirkel (to halvsirkler) med radius $\frac x2$ og areal $\pi ( \frac x2)^2$. Hele boksen har høyden h. Volumet blir da: | |||
$V = Gh = (\pi( \frac x2)^2 + xy)h$ | |||
===b)=== | ===b)=== | ||
Ut fra betingelsene: | |||
$x+y= 10 \Rightarrow y=10-x \\ x+h= 5 \Rightarrow h =5-x$ | |||
Setter dette inn i likningen i a og får kun en ukjent, x: | |||
$V = Gh = (\pi( \frac x2)^2 + xy)h \\ V = (\pi( \frac x2)^2 + x(10-x))(5-x)$ | |||
Ser ikke noe poeng i å multiplisere ut parentesene da Geogebra håndterer produkter ( skal bruke uttrykket i c). | |||
===c)=== | ===c)=== | ||
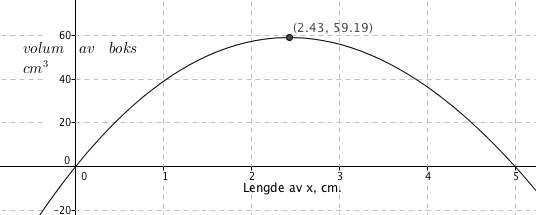
Bruker Geogebra for å finne maksimalpunktet (ekstremalpunkt): | |||
[[File:2p-v15-7c.png]] | |||
Boksen får størst volum når x er 2,4 centimeter. Da er volumet 59,2 kubikkcentimeter. | |||
Siste sideversjon per 26. jul. 2015 kl. 21:33
- Løsningsforslag (pdf) fra joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
Median av seks målinger er gjennomsnittet av måling 3 og 4.
Tre tall er allerede under 7, det betyr at tall nr 3 er 6 (fredag). Det betyr at det må være 8 grader på lørdag, dersom median skal bli 7, fordi 8 + 6 = 14, som delt på to er 7.
Oppgave 2
$x \cdot 0,8= 240 \\ x= \frac{240}{0,8} \\ x= 300$
Når noe settes ned med 20% er vekstfaktoren 0,8. Pris før nedsettelse var derfor 300 kroner.
Oppgave 3
a)
En million er 1 000 000. En milliard er 1000 millioner. 14 milliarder blir da:
$14 \cdot 1000 \cdot 1000000 = 1,4 \cdot 10^{10}$år.
b)
$1,4 \cdot 10^{10} \cdot 3,2 \cdot 10^7 = 4,48 \cdot 10^{17}$ sekunder gammelt.
Oppgave 4
a)
$\frac {3^2-2^3}{2^0 \cdot 4} = \frac{9-8}{4} = \frac 14$
b)
$\frac{(6a)^2 \cdot b^2}{9a \cdot b^{-2}} \\= \frac{6^2a^2b^2}{9ab^{-2}} \\= \frac{36}{9}a^{2-1}b^{2-(-2)} \\ = 4ab^4$
Oppgave 5
a)
En lineær modell er på formen
f(x) = ax + b
Nedgangen er på 60 elever på 10 år, dvs. 6 elever per år. Vi får da:
f(x) = -6x + 1400,
der x er antall år regnet fra 10 år tilbake. Dvs. x=10 er nå.
b)
$ g(x) = 1340 \cdot 0.995^x$
1340 er antall elever nå. 0,995 er vekstfaktoren når noe minker med 0,5%. x er antall år fra nå.
Oppgave 6
a)
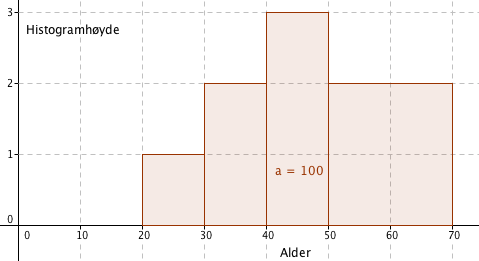
Gjennomsnitt i klassedelt materiale finner man ved å anta at verdiene i hver klasse fordeler seg jevnt rundt klassemidtpunktet. Vi får da:
$Gj = \frac{25 \cdot 10 + 35 \cdot 20 + 45 \cdot 30 + 60 \cdot 40}{100} = \frac{4700}{100} = 47$ år.
b)
c)
| Alder | frekvens | relativ frekvens | kumulativ frekvens |
| [ 20,30> | 10 | $\frac{1}{10}$ | 10 |
| [30, 40> | 20 | $\frac{2}{10}$ | 30 |
| [40,50> | 30 | $\frac{3}{10}$ | 60 |
| [ 50,70> | 40 | $\frac{4}{10}$ | 100 |
Oppgave 7
a)
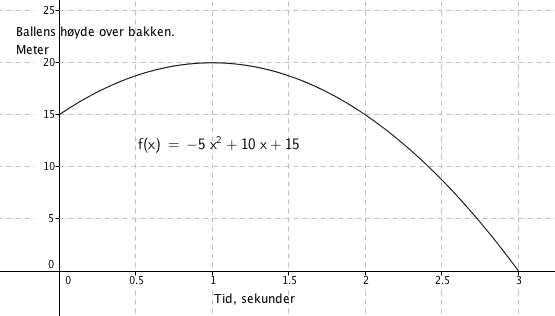
| h | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| h(t) | 15 | 18,75 | 20 | 18,75 | 15 | 8,75 | 0 |
b)
c)
h(0) er i kastøyeblikket. Karl står på en balkong 15 meter over bakken.
h(3), ballen lander. Hele ballens svev tok tre sekunder.
Oppgave 8
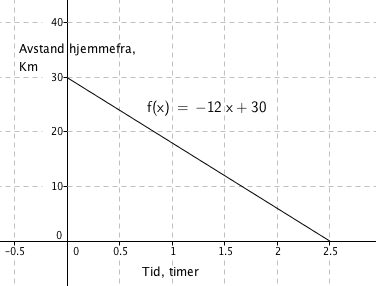
Han starter 30 km hjemmefra og sykler mot hjemmet med konstant fart. Han kommer nærmere og nærmere og er hjemme etter to og en halv time. Funksjonen over viser avstand fra hjemmet f, som funksjon av tiden i timer, x.
DEL TO
Oppgave 1
Per: $3450 $ kr.
Pål: $3000 \cdot 1,022^6 = 3418, 43$ kr.
Espen: $3000 \cdot 1,018^6 + 100 = 3438,93$ kr.
Pål fikk det beste tilbudet.
Oppgave 2
a)
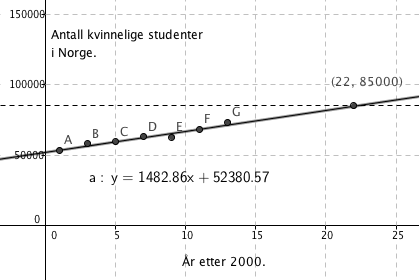
Mulig modell: $y=1482,86x + 52380,57$
b)
Fra stigningstallet i a ser man at økningen per år i gjennomsnitt er ca1480 nye kvinnelige studenter.
c)
Fra Figuren i a ser man at antall kvinnelige studenter forventes å passere 85000 i 2022, forutsatt at modellen holder så langt ( 9år) inn i fremtiden.
Oppgave 3
a)
Gjennomsnittstemperaturen er 19,9 grader celsius, med et standardavvik på 1,7 grader.
b)
Gjennomsnittstemperaturen i by B er 0,9 grader høyere enn i by A, men standardavviket for temperaturdata til by B er dobbelt så stor som for by A. Temperaturen i by B er derfor mere usikker enn den i A. Vi observerer at innenfor et standardavvik forskyves nedre temperatugrense i B med 0,8 grader celsius lavere enn i A.
Oppgave 4
a)
$F_4$ vil ha fire trekanter mere enn $ F_3$, altså $18+ 4 \cdot 3 = 30 $ linjestykker.
b)
Figurene består av en eller flere likesida trekanter. Antall linjestykker øker med 3n, fra en figur til den neste.
c)
d)
$g(20)=1,5 \cdot 20^2+ 1,5 \cdot 20 = 600 + 30= 630$
Oppgave 5
a)
Erstatning minker med 10% per år, derfor vekstfaktor 0,9. x er antall år, derfor $0,9^x$
Erstatningsbeløp når sykkelen er ny er innkjøpspris P, minus egenandel, derfor (P- 2000)
b)
$F(x)=(P-2000) 0,9^x \\ F(7) = (10000 - 2000)0,9^7 \\ F(7) = 3826,38$
Da får man utbetalt ca. 3826 kroner.
c)
$F(x)=(P-2000) 0,9^x -150x$
Det siste leddet er premiekostnadene, 150x.
d)
$F(x)=(P-2000) 0,9^x -150x \\F(13)= 8000 \cdot 0,9^{13} -150 \cdot 13 \\ V(13) = 83,50$
Du får da netto utbetalt 83,50 kroner. Du får egentlig utbetalt i overkant av 2000 kroner, men når man trekker fra det forsikringen har kostet deg sitter du igjen med 83,50. Hva er sannsynligheten for at en 13 år gammel sykkel blir stjålet? Litt avhengig av risikobildet og hvor god sykkellås jeg har ville jeg vurdere å kutte forsikringen etter ca. 5 år.
Oppgave 6
a)
b)
Maks. temp dag 224, og min. temp dag 13. Forskjell: 16,9 - 3,6 = 13,3 grader.
c)
f(100) = 8,5
Det forteller at dag 100 i 2014 hadde en vanntemperatur på 8,5 grader, på det aktuelle stedet.
Den momentane veksten er, ut fra figuren 0,091. Det betyr at vanntemperaturen akkurat denne dagen øker med 0,091 grader. Dette er jo på våren så det er jo naturlig.
Oppgave 7
a)
Grunnflaten av boksen består av et rektangel med areale xy og en sirkel (to halvsirkler) med radius $\frac x2$ og areal $\pi ( \frac x2)^2$. Hele boksen har høyden h. Volumet blir da:
$V = Gh = (\pi( \frac x2)^2 + xy)h$
b)
Ut fra betingelsene: $x+y= 10 \Rightarrow y=10-x \\ x+h= 5 \Rightarrow h =5-x$
Setter dette inn i likningen i a og får kun en ukjent, x:
$V = Gh = (\pi( \frac x2)^2 + xy)h \\ V = (\pi( \frac x2)^2 + x(10-x))(5-x)$
Ser ikke noe poeng i å multiplisere ut parentesene da Geogebra håndterer produkter ( skal bruke uttrykket i c).
c)
Bruker Geogebra for å finne maksimalpunktet (ekstremalpunkt):
Boksen får størst volum når x er 2,4 centimeter. Da er volumet 59,2 kubikkcentimeter.