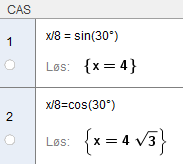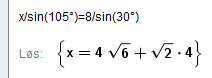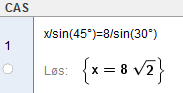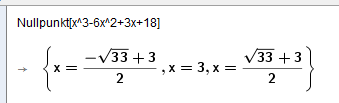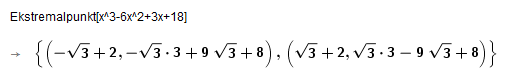1T 2015 vår LØSNING: Forskjell mellom sideversjoner
| (48 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 26: | Linje 26: | ||
<math> \left[ \begin{align*} y=1 \end{align*}\right] </math> | <math> \left[ \begin{align*} y=1 \end{align*}\right] </math> | ||
Innsatt i | Innsatt i første likning gir det x=-5, dvs: | ||
$x= -5 \wedge y= 1$ | $x= -5 \wedge y= 1$ | ||
| Linje 59: | Linje 59: | ||
$lg(x^2-0,9) = -1 \\ 10^{lg(x^2-0,9} = 10^{-1} \\ x^2- 0,9 = 0,1 \\ x^2 =1 \\x = \pm 1$ | $lg(x^2-0,9) = -1 \\ 10^{lg(x^2-0,9)} = 10^{-1} \\ x^2- 0,9 = 0,1 \\ x^2 =1 \\x = \pm 1$ | ||
Vi kan ikke ta logaritmen til et negativt tall, og | Vi kan ikke ta logaritmen til et negativt tall, og må sjekke begge løsningene. I dette tilfellet kan begge løsninger brukes: | ||
$x= - 1 \vee x=1$ | $x= - 1 \vee x=1$ | ||
| Linje 71: | Linje 71: | ||
$x^2+bx+16$ | $x^2+bx+16$ | ||
Vi registrerer at $16 = | Vi registrerer at $16 = (\pm4)^2 $. Da må b være lik 2 multiplisert med $\pm 4$, i følge kvadratsetningene. | ||
$x^2 | $x^2 \pm 8x+16 = (x \pm4)^2$ | ||
b er altså lik | b er altså lik $ \pm8$ | ||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 84: | Linje 84: | ||
==Oppgave 8== | ==Oppgave 8== | ||
$\frac{x^2-12x+36}{ | $\frac{x^2-12x+36}{2x^2 - 72} \\= \frac{(x-6)(x-6)}{2(x+6)(x-6)} \\ =\frac{x-6}{2(x+6)}$ | ||
==Oppgave 9== | ==Oppgave 9== | ||
| Linje 104: | Linje 104: | ||
===a)=== | ===a)=== | ||
Bruker Pytagoras på trekant ABC og får: | |||
AB = $\sqrt{2^2-1^2} = \sqrt 3$ | |||
Bruker Pytagoras på trekant DEF og får: | |||
DF = $\sqrt{1^2 + 1^2} = \sqrt 2$ | |||
===b)=== | ===b)=== | ||
Cosinus til en vinkel er hosliggende katet delt på hypotenus. | |||
Sinus til en vinkel er motstående katet delt på hypotenus. | |||
Tangens til en vinkel er motstående katet delt på hosliggende katet. | |||
{| width="auto" | {| width="auto" | ||
| Linje 130: | Linje 143: | ||
==Oppgave 11== | ==Oppgave 11== | ||
===a)=== | |||
Trekker to, sannsynlighet for ikke "Jump": | |||
P( ikke Jump) = $\frac 69 \cdot \frac 58 = \frac 13 \cdot \frac 54 = \frac 5{12}$ | |||
===b)=== | |||
P ('"surf" og "catch") = $ \frac 29 \cdot \frac48 + \frac 49 \cdot \frac 28 = \frac 19 + \frac 19 = \frac 29 $ | |||
===c)=== | |||
P( to like flasker) = $\frac 29 \cdot \frac 18 + \frac 39 \cdot \frac 28 + \frac 49 \cdot \frac 38 \\ \frac1{36} + \frac 3{36} + \frac 6{36} = \frac{10}{36} = \frac {5}{18}$ | |||
==Oppgave 12== | ==Oppgave 12== | ||
$f(x)= -2x^2+4x+6$ | |||
===a)=== | |||
Skjæring med y - akse: | |||
x = 0 som gir punktet (0,6). | |||
f(0) = 6 | |||
Skjæring med x - akse: | |||
f(x) = 0 | |||
===b)=== | |||
[[File:1t-v15-12bc.png]] | |||
===c)=== | |||
Vi ser fra figuren i b at f(x) = g(x) har løsninger for x = -1 og for x = 2. | |||
==Oppgave 13== | ==Oppgave 13== | ||
| Linje 139: | Linje 189: | ||
$O = 2\pi r$ | $O = 2\pi r$ | ||
Dersom vi forlenger tauet med 20 meter blir ny omkrets: O + 20. Vi må da finne | Dersom vi forlenger tauet med 20 meter blir ny omkrets: O + 20. Vi må da finne tilhørende radius. | ||
$r= \frac{O}{2 \pi}$ | $r= \frac{O}{2 \pi}$ | ||
| Linje 152: | Linje 202: | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
80 personer. | |||
1,045 tilsvarerer en vekst på 4,5% | |||
===b)=== | |||
$f(61) = 80 \cdot 1,045^{61} = 1173$ | |||
Ja, antallet vil være ca 1170. | |||
===c)=== | |||
[[File: 1t-v15-1c.png]] | |||
f(16) forteller hvor mange "likes" det var 16. april, 162. | |||
f´(16) forteller om den momentane endringen denne dagen, en økning på ca 7 "likes". | |||
==Oppgave 2== | ==Oppgave 2== | ||
Fra ungdomskolen vet man at når vinklene i en trekant er 30, 60 og 90 grader, er korteste katet halvparten av hypotenusens lengde. Dvs. BC = 4. | |||
Bruker pytagoras på trekanten BCD og finner at $CD = \sqrt{64-16} = \sqrt{48} = 4 \sqrt {3}$ | |||
Men, oppgaven krever CAS, så da må vi taste litt... : | |||
[[File: 1t-v2015-2.png]] | |||
Som er i sammsvar med hva vi fant over. | |||
Finner så AB: | |||
[[File: 1t-v2015-2-3.png]] | |||
Finner så AD: | |||
[[File: 1t-v2015-2-2.png]] | |||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | |||
[[File:1t-v15-3a.png]] | |||
Nullpunkter: (-1,37 , 0) og (4,37 , 0) | |||
Ekstremalpunkter: Maksimum: (0,27 , 18,39) , Minimum: (3,73 , -2,39) | |||
===b)=== | |||
[[File:1t-v2015-3b.png]] | |||
[[File:1t-v2015-3b-2.png]] | |||
Eksakt ekstremalpunkt: | |||
Maksimumspunkt: $(2- \sqrt 3, 8 + 6 \sqrt 3)$ | |||
Minimumspunkt: $(2 + \sqrt 3, 8 - 6 \sqrt 3)$ | |||
===c)=== | |||
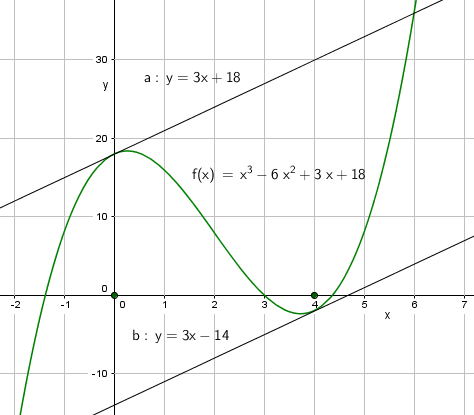
[[File:1t-v2015-3c.png]] | |||
Tangenter med stigningstall 3: | |||
y = 3x - 14 | |||
og | |||
y = 3x + 18 | |||
===d)=== | |||
[[File:1t-v2015-3d.png]] | |||
==Oppgave 4== | ==Oppgave 4== | ||
Antall små is : x | |||
Antall store is: y | |||
20 liter is gir $12 \cdot 20 = 240$ kuler. | |||
2x + 3y = 240 | |||
Liten is koster 24 kroner og stor is 32 kroner. Hun solgte for 2752 kroner: | |||
24x + 32y = 2752 | |||
Vi kan bruke CAS verktøyet i Geogebra: | |||
[[File:1t-v15-4.png]] | |||
Det blir solgt 32 store is, og 72 små is den dagen. | |||
==Oppgave 5== | ==Oppgave 5== | ||
Vi har symmetri og tre sirkler. | |||
Arealet av sirkel med diameter a: $A_{AD}=\pi r^2 = \pi \frac{a^2}{4} $ | |||
Areal av sort område: $A_{skravert} = A_{AC} - A_{AB} = \frac{\pi a^2}{9} - \frac{\pi a^2}{36} = \frac{\pi a^2}{12} $ | |||
12:4 = 3, dvs. forholdet mellom arealet av sirkelen og det skraverte området er 3. | |||
Siste sideversjon per 30. aug. 2015 kl. 12:55
Løsning laget av mattepratbruker LektorH
DEL EN
Oppgave 1
$\frac{7,5 \cdot 10^{15}}{0,003} \\= \frac{7,5}{3} \cdot 10^{15+3} \\ = 2,5 \cdot 10^{18}$
Oppgave 2
<math> \left[ \begin{align*}x+6y=1 \\ 2x+4y=-6 \end{align*}\right] </math>
<math> \left[ \begin{align*} x= 1-6y \\ 2(1-6y)+4y=-6\end{align*}\right] </math>
<math> \left[ \begin{align*} x= 1-6y \\ 2-12y+4y= -6 \end{align*}\right] </math>
<math> \left[ \begin{align*} y=1 \end{align*}\right] </math>
Innsatt i første likning gir det x=-5, dvs:
$x= -5 \wedge y= 1$
Oppgave 3
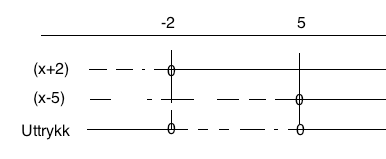
$x^2-3x-10 >0$
Løser andregradslikningen: $x^2-3x-10=0 \\ x= \frac{3 \pm \sqrt{9+40}}{2} \\ x= \frac{3 \pm 7}{2} \\ x= -2 \vee x= 5$
Vi observerer at uttrykket skulle være større enn null: $x \in < \leftarrow, -2> \cup <5, \rightarrow>$
Oppgave 4
a)
$4^{\frac12} \cdot 8^0 \cdot 2^{-1} \cdot \sqrt[4]{16} \\ = 2 \cdot 1 \cdot 0,5 \cdot 2 \\=2 $
b)
$\sqrt{18}\cdot \sqrt 2 + \frac{\sqrt{72}}{\sqrt 8} \\= \sqrt{18 \cdot 2} + \sqrt{\frac{72}{8}} \\ = 6+3=9$
Oppgave 5
$lg(x^2-0,9) = -1 \\ 10^{lg(x^2-0,9)} = 10^{-1} \\ x^2- 0,9 = 0,1 \\ x^2 =1 \\x = \pm 1$
Vi kan ikke ta logaritmen til et negativt tall, og må sjekke begge løsningene. I dette tilfellet kan begge løsninger brukes:
$x= - 1 \vee x=1$
Oppgave 6
$x^2+bx+16$
Vi registrerer at $16 = (\pm4)^2 $. Da må b være lik 2 multiplisert med $\pm 4$, i følge kvadratsetningene.
$x^2 \pm 8x+16 = (x \pm4)^2$
b er altså lik $ \pm8$
Oppgave 7
$2x(x-2)-(x-2)(2x+1) \\ = 2x^2 -4x- ( 2x^2+x-4x-2) \\= 2x^2 -4x-2x^2-x+4x+2 \\ = -x+2$
Oppgave 8
$\frac{x^2-12x+36}{2x^2 - 72} \\= \frac{(x-6)(x-6)}{2(x+6)(x-6)} \\ =\frac{x-6}{2(x+6)}$
Oppgave 9
En rett linje har likningen :
y = ax + b
Stigningstall er: a = $\frac{\Delta y}{ \Delta x} = \frac {4-2}{3-(-1)} = \frac 12$
Bruker x og y verdi i første punkt og finner b:
$2 = \frac 12 \cdot -1 + b \\ b = \frac 52$
$y= \frac 12x + \frac 52$
Oppgave 10
a)
Bruker Pytagoras på trekant ABC og får:
AB = $\sqrt{2^2-1^2} = \sqrt 3$
Bruker Pytagoras på trekant DEF og får:
DF = $\sqrt{1^2 + 1^2} = \sqrt 2$
b)
Cosinus til en vinkel er hosliggende katet delt på hypotenus.
Sinus til en vinkel er motstående katet delt på hypotenus.
Tangens til en vinkel er motstående katet delt på hosliggende katet.
| u | sin u | cos u | tan u |
| $30^{\circ}$ | $\frac 12$ | $\frac{\sqrt 3}{2}$ | $\frac{1}{\sqrt 3}$ |
| $45^{\circ}$ | $\frac{\sqrt 2}{2}$ | $\frac{\sqrt 2}{2}$ | 1 |
| $60^{\circ}$ | $\frac{\sqrt 3}{2}$ | $\frac 12$ | $\sqrt 3$ |
Oppgave 11
a)
Trekker to, sannsynlighet for ikke "Jump":
P( ikke Jump) = $\frac 69 \cdot \frac 58 = \frac 13 \cdot \frac 54 = \frac 5{12}$
b)
P ('"surf" og "catch") = $ \frac 29 \cdot \frac48 + \frac 49 \cdot \frac 28 = \frac 19 + \frac 19 = \frac 29 $
c)
P( to like flasker) = $\frac 29 \cdot \frac 18 + \frac 39 \cdot \frac 28 + \frac 49 \cdot \frac 38 \\ \frac1{36} + \frac 3{36} + \frac 6{36} = \frac{10}{36} = \frac {5}{18}$
Oppgave 12
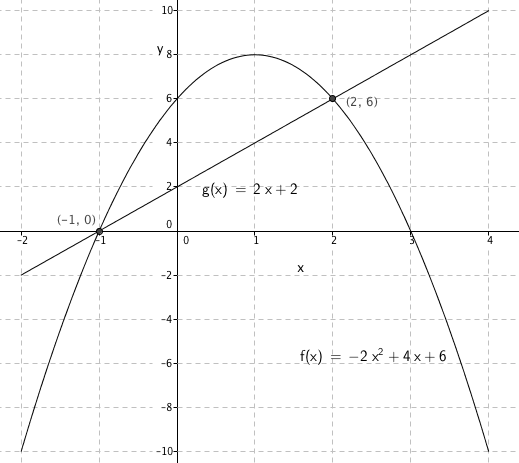
$f(x)= -2x^2+4x+6$
a)
Skjæring med y - akse:
x = 0 som gir punktet (0,6).
f(0) = 6
Skjæring med x - akse:
f(x) = 0
b)
c)
Vi ser fra figuren i b at f(x) = g(x) har løsninger for x = -1 og for x = 2.
Oppgave 13
Jordens radius er r, og omkretsen er O.
$O = 2\pi r$
Dersom vi forlenger tauet med 20 meter blir ny omkrets: O + 20. Vi må da finne tilhørende radius.
$r= \frac{O}{2 \pi}$
Ny radius blir:
$r_{20} = \frac{O+20}{2 \pi} = \frac{O}{2 \pi} + \frac{10}{\pi} $
Tauet vil være ca. 3 meter over bakkenivå så det vil være mulig å gå under tauet.
DEL TO
Oppgave 1
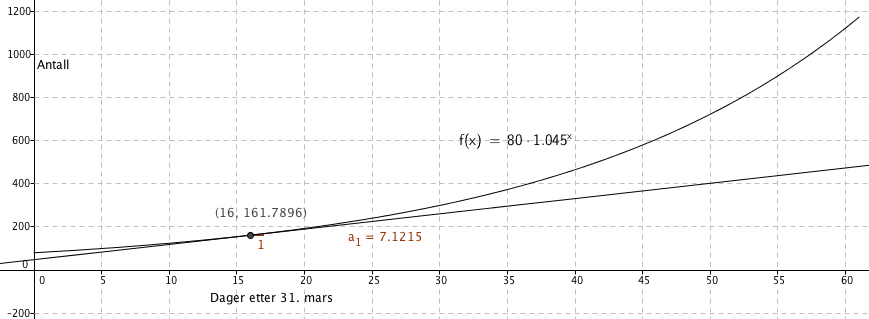
a)
80 personer.
1,045 tilsvarerer en vekst på 4,5%
b)
$f(61) = 80 \cdot 1,045^{61} = 1173$
Ja, antallet vil være ca 1170.
c)
f(16) forteller hvor mange "likes" det var 16. april, 162.
f´(16) forteller om den momentane endringen denne dagen, en økning på ca 7 "likes".
Oppgave 2
Fra ungdomskolen vet man at når vinklene i en trekant er 30, 60 og 90 grader, er korteste katet halvparten av hypotenusens lengde. Dvs. BC = 4.
Bruker pytagoras på trekanten BCD og finner at $CD = \sqrt{64-16} = \sqrt{48} = 4 \sqrt {3}$
Men, oppgaven krever CAS, så da må vi taste litt... :
Som er i sammsvar med hva vi fant over.
Finner så AB:
Finner så AD:
Oppgave 3
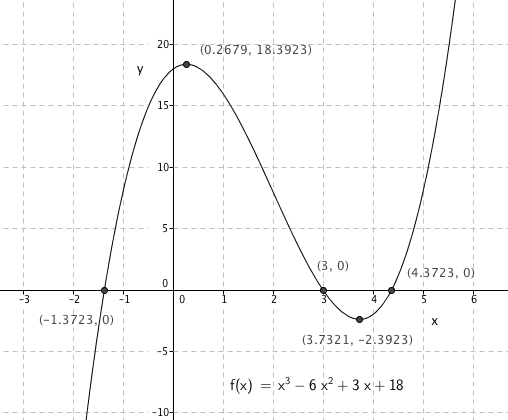
a)
Nullpunkter: (-1,37 , 0) og (4,37 , 0)
Ekstremalpunkter: Maksimum: (0,27 , 18,39) , Minimum: (3,73 , -2,39)
b)
Eksakt ekstremalpunkt:
Maksimumspunkt: $(2- \sqrt 3, 8 + 6 \sqrt 3)$
Minimumspunkt: $(2 + \sqrt 3, 8 - 6 \sqrt 3)$
c)
Tangenter med stigningstall 3:
y = 3x - 14
og
y = 3x + 18
d)
Oppgave 4
Antall små is : x
Antall store is: y
20 liter is gir $12 \cdot 20 = 240$ kuler.
2x + 3y = 240
Liten is koster 24 kroner og stor is 32 kroner. Hun solgte for 2752 kroner:
24x + 32y = 2752
Vi kan bruke CAS verktøyet i Geogebra:
Det blir solgt 32 store is, og 72 små is den dagen.
Oppgave 5
Vi har symmetri og tre sirkler.
Arealet av sirkel med diameter a: $A_{AD}=\pi r^2 = \pi \frac{a^2}{4} $
Areal av sort område: $A_{skravert} = A_{AC} - A_{AB} = \frac{\pi a^2}{9} - \frac{\pi a^2}{36} = \frac{\pi a^2}{12} $
12:4 = 3, dvs. forholdet mellom arealet av sirkelen og det skraverte området er 3.