R1 2014 vår LØSNING: Forskjell mellom sideversjoner
| (117 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://ndla.no/nb/node/140553?fag=57933 Løsning fra NDLA] | |||
[http://www.matematikk.net/matteprat/download/file.php?id=291 løsning som pdf laget av mattepratbruker claves] | [http://www.matematikk.net/matteprat/download/file.php?id=291 løsning som pdf laget av mattepratbruker claves] | ||
| Linje 7: | Linje 9: | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
$f(x)= ln(x^2+x) \\ f´(x)= \frac{1\cdot ( 2x+1)}{x^2+x} = \frac{2x+1}{x^2+x}$ | |||
===b)=== | |||
$g(x)= x \cdot e^x \\ g´(x)= e^x + xe^x = e^x (1+x)$ | |||
===c)=== | |||
$h(x)= (x^2+3)^4 \\ h´(x)= 4(x^2+3)^3 \cdot 2x = 8x(x^2+3)^3$ | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | |||
$P(x)= x^3-7x^2+14x-8 $ | |||
En går opp i -8, og P(1) = 1 - 7 + 14 -8 = 0. | |||
P har et nullpunkt for x = 1 | |||
===b)=== | |||
$x^3-7x^2+14x-8 : (x-1)= x^2-6x+8 \\ -(x^3-x^2) \\ \quad \quad -6x^2+14x \\ \quad \quad -(6x^2+6x) \\ \quad \quad \quad \quad \quad 8x-8 $ | |||
Abc formel eller lignende gir følgende førstegradsfaktorer: | |||
P(x)= (x-1)(x- 2)(x- 4) | |||
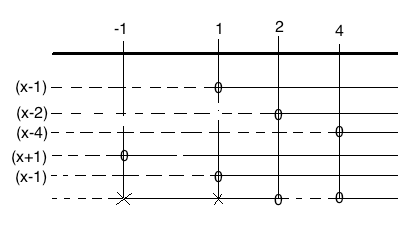
===c)=== | |||
[[File:r1-v2014-12c.png]] | |||
$x \in < -1, 1> \cup <1,2] \cup [4, \rightarrow>$ | |||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | |||
$-2 \vec a + \vec b= -2[-2,1] + [3,6] = [4, -2] + [3,6] = [7, 4] $ | |||
Skalarprodukt: | |||
$ \vec a \cdot \vec b = [-2,1]\cdot[3,6] = -6 + 6 =0$ | |||
===b)=== | |||
$\vec b || \vec c \\ s[3,6] = [k-1, 4] \\ s = \frac 23 \wedge k = 3$ | |||
===c)=== | |||
k slik at $| \vec c| = |2 \vec a| \\ \sqrt{(k-1)^2 + 16} = \sqrt{16+ 4} \\ (k-1)^2 = 4 \\ k-1 = \pm 2 \\ k= -1 \vee k = 3$ | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
$f(x)= 3x^4-6x^2 = 3x^2(x^2-2) \\ f(x)=0 \\ x=0 \vee x= - \sqrt 2 \vee x = \sqrt 2$ | |||
===b)=== | |||
$f´(x) = 12x^3-12x = 12x(x^2-1)$ | |||
Vi ser at f har ekstremalpunkter for x = 0 og for $x = \pm 1$ | |||
f(0) = 0 , dette er også et nullpunkt. | |||
f( -1) = f( 1) = -3 | |||
Da må (0,0) vare et maksimumspunkt, og (-1, -3) og (1, -3) er minimumspunkter (kan se det uten fortegnsskjema, siden (0,0) også er et nullpunkt). | |||
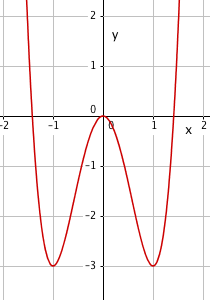
===c)=== | |||
[[File:r1-v2014-14c.png]] | |||
==Oppgave 5== | ==Oppgave 5== | ||
Trekanten ABS er likebeint. Vinkel BAS er 27 grader. Vinkel S er 180 - 54 = 126 grader. S er en sentralvinkel. Vinkelen ACB er en pereferivinkel som spenner over samme bue som S og er derfor 63 grader. | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
p er oddetall større enn 1. Både p - 1 og p + 1 vil da være partall. Alle partall er delelige på 2 og kan skrives på formen 2n, der n er et naturlig tall. Derfor vil | |||
$ \frac{p+1}{2} \wedge \frac{p -1}{2}$ være hele tall. | |||
===b)=== | |||
$( \frac{p+1}{2})^2 - ( \frac{p-1}{2})^2 = (\frac{p+1+p-1}{2})( \frac{p+1-p+1}{2}) =p$ | |||
$( \frac{151+1}{2})^2 - ( \frac{151-1}{2})^2 = 76^2 - 75^2$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
$H(x)=x^x \quad x>0 \\ h(x)= (e^{lnx})^x = e^{x lnx}$ | |||
(sjekk potensreglene) | |||
===b)=== | |||
$h´(x) = (e^{u})´\cdot u´\\ h´(x) = e^{x lnx}(lnx + \frac 1x \cdot x) = x^x(lnx +1)$ | |||
==DEL TO== | ==DEL TO== | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
$D: (0,y) \\ \vec{BA} = [-4,4] \\ \vec{CD} = [-4,y-4]$ | |||
For parallelle vektorer er det slik at det finnes en konstant k som multiplisert med den ene vektoren gir den andre vektoren. I dette tilfelle må k være lik 1, siden førstekoordinatene i begge vektorene er like, -4. Får da at 4= y-4, dvs y= 8. | |||
D: (0,8) | |||
===b)=== | |||
$\vec{BC} = [-1,5] \\ \vec{OM} = \vec{OB} +\frac 12 \vec{BC } = [5,-1] +\frac 12 [-1,5] = [ \frac{9}{2}, \frac{3}{2}]$ | |||
Koordinatene til M er : $(\frac{9}{2},\frac {3}{2})$ | |||
===c)=== | |||
$\vec{AM} =[\frac 92 - 1, \frac 32 - 3]=[ \frac 72, - \frac 32 ] \\ \vec{OP} = \vec{OM} + \vec{MP} = \vec{OM} +3 \vec{AM} \\ \vec{OP} = [\frac 39, \frac 32] +3[\frac 72,- \frac 32] = [15, -3]$ | |||
Koordinatene til P er (15, -3). | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | |||
Hypergeometrisk situasjon: | |||
$\frac{\binom{12}{1} \binom{16}{4}}{\binom{28}{5}} = 0,222$ | |||
Det er 22,2% sannsynlig at akkurat en gutt blir med i gruppen. | |||
===b)=== | |||
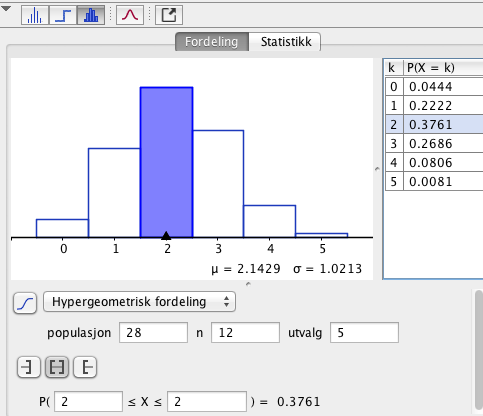
Løser denne enklest med sannsynlighetskalkulatoren i Geogebra. $\frac{44}{117} \approx 0,3716$ | |||
[[File:r1-v2014-22b.png]] | |||
Det blir med to gutter. | |||
===c)=== | |||
Vi vet at Betsy er med, derfor betinget. Fortsatt hypergeometrisk situasjon. Det er det 27 elever igjen, fire skal trekkes, en av dem skal være Arne: | |||
$\frac{\binom{1}{1} \binom{26}{3}}{\binom{27}{4}} = 0,1481$ | |||
Det er 14,8% sannsynlig at Arne også blir med. | |||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | |||
$f(x)= 6x \cdot e^{- \frac{x^2}{8}} \\ f´(x)= 6e^{- \frac{x^2}{8}} + 6x \cdot e^{- \frac{x^2}{8}} \cdot (- \frac x4) \\ f´(x)=6e^{- \frac{x^2}{8}} - \frac 32 x^2e^{- \frac{x^2}{8}} \\ f´(x)= \frac 32(4-x^2)e^{- \frac{x^2}{8}}$ | |||
===b)=== | |||
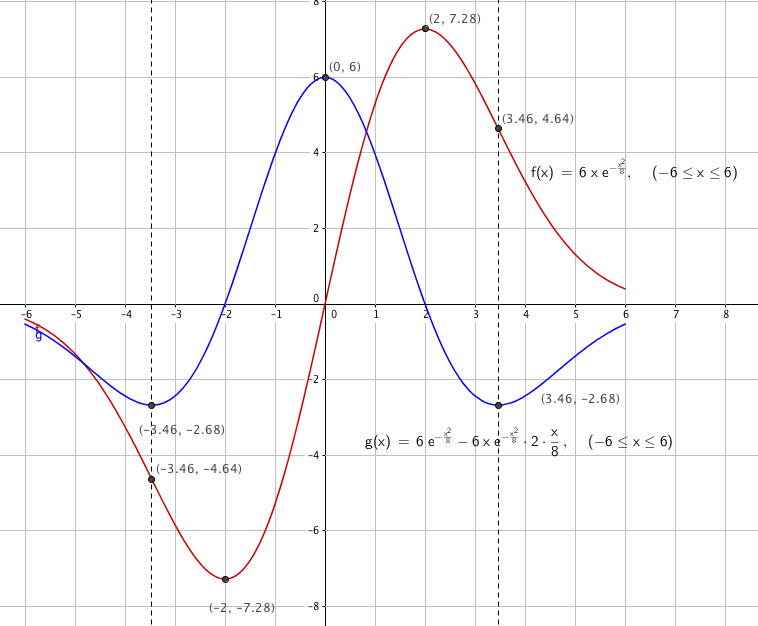
[[File:r1-v2014-23abc2.png]] | |||
Figuren vis f(x) (rød graf) og Grafen til f´(x)=g(x) (blå), i samme koordinatsystem. | |||
===c)=== | |||
Den deriverte til f(x), g(x) er null for x = -2 og for x = 2. Det betyr at disse er ekstremalpunkter. til f. Fra grafen ser vi at f ha et minimumspunkt for i ( -2, -7.28), og et maksimumspunkt i (2, 7.28). Tilgi meg for å ha brukt en fornuftig, men etter norsk standard feil desimalnotasjon. | |||
Vendepunktene til f finner vi der den deriverte til f, g har ekstremalpunkter, x= -3,46, x= 0 og x= 3,46, noe som gir følgene vendepunkter: | |||
(-3.46, -4.46) fra hul siden ned til opp, | |||
(0,0) fra hul side opp til ned, og | |||
(3.46, 4.46) fra hul side ned til opp. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
Benevningen er desimeter, dm, i resten av oppgaven er benevninger utelatt. | |||
Overflaten av boksen består av en bunn med areal $x^2$ og fire sideflater med arealet $xh$. Overflaten blir da $x^2+ 4xh$, og siden det samlede arealet skal være 12 får vi: | |||
$x^2+4xh=12$ | |||
Uttrykk for h: | |||
$x^2+4xh=12 \\ 4xh= 12-x^2 \\ h = \frac{12-x^2}{4x} \\ h=\frac{3}{x} - \frac{x}{4}$ | |||
===b)=== | |||
$x^2$ må være større enn null og mindre enn tolv, dvs $0<x< \sqrt {12}$. | |||
===c)=== | |||
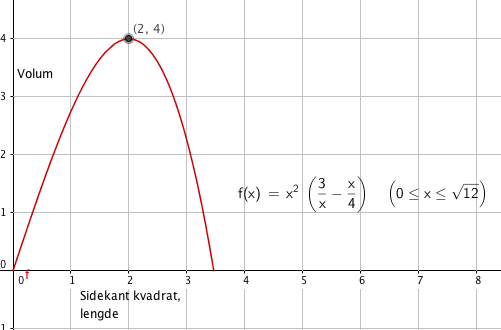
[[File:r1-v2014-24c.png]] | |||
Det spørres ikke om grafen over, men det kan være greit å se hvordan ting ser ut... | |||
Volum av kar: $V(x) = x^2h= x^2( \frac 3x - \frac x4) = 3x - \frac{x^3}{4}$ | |||
===d)=== | |||
$V´(x)= 3 - \frac 34x^2 \\ V´(x)=0 \\ 3- \frac 34 x^2 =0 \\ x = \pm 2$ | |||
Bruker den positive verdien for x og finner at V(2) = 4. Siden alle mål var i dm. tilsvarer dette 4 liter. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
Ballen treffer bakken når y-koordinaten til posisjonsvektoren er null: $15-4,9t^2 =0 \\ t^2 = \frac{15}{4,9} \\t = \pm 1,75$ | |||
Den treffer bakken etter 1,75 sekunder. | |||
===b)=== | |||
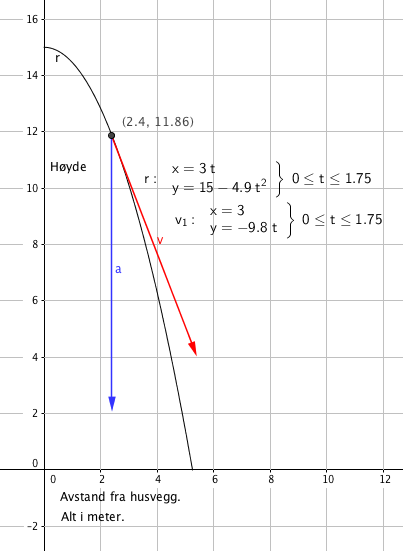
[[File:r1-v2014-25bcd.png]] | |||
===c)=== | |||
For tegning av fartsvektor se figur i b. Fartsvektoren er den deriverte av posisjonsvektoren. Fartsvektoren blir da [3,9.8t] = [3, 7.84]. | |||
For å finne banefarten bruker vi Pytagoras og finner at den er $|v|=+ \sqrt{3^2+7,84^2} = 8,39 $. | |||
Vinkelen til farten er: $tan \alpha = \frac{3}{7,84} \\ \alpha \approx 21^{\circ}$ | |||
Farten er 8,39 m/s og har en retning på ca 21 grader fra husveggen (loddlinjen eller vertikal akse). | |||
===d)=== | |||
Tyngdens akselerasjon virker. Den er $9,81 m/s^2$, nedover, altså i y- retning. Dersom man deriverer fartsvektoren får man en x komponent lik null og en y komponent lik - 9,8 (fordi positiv retning er oppover og akselerasjonen er nedover.) | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | ===a)=== | ||
$n^n \cdot ( \frac xn)^{lgx} = x^n \\ ( \frac xn)^{lgx} = ( \frac xn)^n \\ lg ( \frac xn)^{lgx} = lg ( \frac xn)^n$ | |||
===b)=== | ===b)=== | ||
$ \lg ( \frac xn)^{\lg x} = \lg ( \frac xn)^n \\ \lg x( \lg x - \lg n) = n( \lg x - \lg n) \\ \lg x(\lg x - \lg n) - n(\lg x-\lg n)=0 \\ (\lg x - n)( \lg x - \lg n)=0$ | |||
===c)=== | ===c)=== | ||
$lgx - n =0 \\ lgx =n \\ x= 10^n$ | |||
eller | |||
$lgx - lgn = 0 \\ x = n$ | |||
Siste sideversjon per 2. mai 2016 kl. 12:47
løsning som pdf laget av mattepratbruker claves
Diskusjon om denne oppgaven på matteprat
DEL EN
Oppgave 1
a)
$f(x)= ln(x^2+x) \\ f´(x)= \frac{1\cdot ( 2x+1)}{x^2+x} = \frac{2x+1}{x^2+x}$
b)
$g(x)= x \cdot e^x \\ g´(x)= e^x + xe^x = e^x (1+x)$
c)
$h(x)= (x^2+3)^4 \\ h´(x)= 4(x^2+3)^3 \cdot 2x = 8x(x^2+3)^3$
Oppgave 2
a)
$P(x)= x^3-7x^2+14x-8 $
En går opp i -8, og P(1) = 1 - 7 + 14 -8 = 0.
P har et nullpunkt for x = 1
b)
$x^3-7x^2+14x-8 : (x-1)= x^2-6x+8 \\ -(x^3-x^2) \\ \quad \quad -6x^2+14x \\ \quad \quad -(6x^2+6x) \\ \quad \quad \quad \quad \quad 8x-8 $
Abc formel eller lignende gir følgende førstegradsfaktorer:
P(x)= (x-1)(x- 2)(x- 4)
c)
$x \in < -1, 1> \cup <1,2] \cup [4, \rightarrow>$
Oppgave 3
a)
$-2 \vec a + \vec b= -2[-2,1] + [3,6] = [4, -2] + [3,6] = [7, 4] $
Skalarprodukt:
$ \vec a \cdot \vec b = [-2,1]\cdot[3,6] = -6 + 6 =0$
b)
$\vec b || \vec c \\ s[3,6] = [k-1, 4] \\ s = \frac 23 \wedge k = 3$
c)
k slik at $| \vec c| = |2 \vec a| \\ \sqrt{(k-1)^2 + 16} = \sqrt{16+ 4} \\ (k-1)^2 = 4 \\ k-1 = \pm 2 \\ k= -1 \vee k = 3$
Oppgave 4
a)
$f(x)= 3x^4-6x^2 = 3x^2(x^2-2) \\ f(x)=0 \\ x=0 \vee x= - \sqrt 2 \vee x = \sqrt 2$
b)
$f´(x) = 12x^3-12x = 12x(x^2-1)$
Vi ser at f har ekstremalpunkter for x = 0 og for $x = \pm 1$
f(0) = 0 , dette er også et nullpunkt.
f( -1) = f( 1) = -3
Da må (0,0) vare et maksimumspunkt, og (-1, -3) og (1, -3) er minimumspunkter (kan se det uten fortegnsskjema, siden (0,0) også er et nullpunkt).
c)
Oppgave 5
Trekanten ABS er likebeint. Vinkel BAS er 27 grader. Vinkel S er 180 - 54 = 126 grader. S er en sentralvinkel. Vinkelen ACB er en pereferivinkel som spenner over samme bue som S og er derfor 63 grader.
Oppgave 6
a)
p er oddetall større enn 1. Både p - 1 og p + 1 vil da være partall. Alle partall er delelige på 2 og kan skrives på formen 2n, der n er et naturlig tall. Derfor vil
$ \frac{p+1}{2} \wedge \frac{p -1}{2}$ være hele tall.
b)
$( \frac{p+1}{2})^2 - ( \frac{p-1}{2})^2 = (\frac{p+1+p-1}{2})( \frac{p+1-p+1}{2}) =p$
$( \frac{151+1}{2})^2 - ( \frac{151-1}{2})^2 = 76^2 - 75^2$
Oppgave 7
a)
$H(x)=x^x \quad x>0 \\ h(x)= (e^{lnx})^x = e^{x lnx}$
(sjekk potensreglene)
b)
$h´(x) = (e^{u})´\cdot u´\\ h´(x) = e^{x lnx}(lnx + \frac 1x \cdot x) = x^x(lnx +1)$
DEL TO
Oppgave 1
a)
$D: (0,y) \\ \vec{BA} = [-4,4] \\ \vec{CD} = [-4,y-4]$
For parallelle vektorer er det slik at det finnes en konstant k som multiplisert med den ene vektoren gir den andre vektoren. I dette tilfelle må k være lik 1, siden førstekoordinatene i begge vektorene er like, -4. Får da at 4= y-4, dvs y= 8.
D: (0,8)
b)
$\vec{BC} = [-1,5] \\ \vec{OM} = \vec{OB} +\frac 12 \vec{BC } = [5,-1] +\frac 12 [-1,5] = [ \frac{9}{2}, \frac{3}{2}]$
Koordinatene til M er : $(\frac{9}{2},\frac {3}{2})$
c)
$\vec{AM} =[\frac 92 - 1, \frac 32 - 3]=[ \frac 72, - \frac 32 ] \\ \vec{OP} = \vec{OM} + \vec{MP} = \vec{OM} +3 \vec{AM} \\ \vec{OP} = [\frac 39, \frac 32] +3[\frac 72,- \frac 32] = [15, -3]$
Koordinatene til P er (15, -3).
Oppgave 2
a)
Hypergeometrisk situasjon:
$\frac{\binom{12}{1} \binom{16}{4}}{\binom{28}{5}} = 0,222$
Det er 22,2% sannsynlig at akkurat en gutt blir med i gruppen.
b)
Løser denne enklest med sannsynlighetskalkulatoren i Geogebra. $\frac{44}{117} \approx 0,3716$
Det blir med to gutter.
c)
Vi vet at Betsy er med, derfor betinget. Fortsatt hypergeometrisk situasjon. Det er det 27 elever igjen, fire skal trekkes, en av dem skal være Arne:
$\frac{\binom{1}{1} \binom{26}{3}}{\binom{27}{4}} = 0,1481$
Det er 14,8% sannsynlig at Arne også blir med.
Oppgave 3
a)
$f(x)= 6x \cdot e^{- \frac{x^2}{8}} \\ f´(x)= 6e^{- \frac{x^2}{8}} + 6x \cdot e^{- \frac{x^2}{8}} \cdot (- \frac x4) \\ f´(x)=6e^{- \frac{x^2}{8}} - \frac 32 x^2e^{- \frac{x^2}{8}} \\ f´(x)= \frac 32(4-x^2)e^{- \frac{x^2}{8}}$
b)
Figuren vis f(x) (rød graf) og Grafen til f´(x)=g(x) (blå), i samme koordinatsystem.
c)
Den deriverte til f(x), g(x) er null for x = -2 og for x = 2. Det betyr at disse er ekstremalpunkter. til f. Fra grafen ser vi at f ha et minimumspunkt for i ( -2, -7.28), og et maksimumspunkt i (2, 7.28). Tilgi meg for å ha brukt en fornuftig, men etter norsk standard feil desimalnotasjon.
Vendepunktene til f finner vi der den deriverte til f, g har ekstremalpunkter, x= -3,46, x= 0 og x= 3,46, noe som gir følgene vendepunkter:
(-3.46, -4.46) fra hul siden ned til opp,
(0,0) fra hul side opp til ned, og
(3.46, 4.46) fra hul side ned til opp.
Oppgave 4
a)
Benevningen er desimeter, dm, i resten av oppgaven er benevninger utelatt.
Overflaten av boksen består av en bunn med areal $x^2$ og fire sideflater med arealet $xh$. Overflaten blir da $x^2+ 4xh$, og siden det samlede arealet skal være 12 får vi:
$x^2+4xh=12$
Uttrykk for h:
$x^2+4xh=12 \\ 4xh= 12-x^2 \\ h = \frac{12-x^2}{4x} \\ h=\frac{3}{x} - \frac{x}{4}$
b)
$x^2$ må være større enn null og mindre enn tolv, dvs $0<x< \sqrt {12}$.
c)
Det spørres ikke om grafen over, men det kan være greit å se hvordan ting ser ut...
Volum av kar: $V(x) = x^2h= x^2( \frac 3x - \frac x4) = 3x - \frac{x^3}{4}$
d)
$V´(x)= 3 - \frac 34x^2 \\ V´(x)=0 \\ 3- \frac 34 x^2 =0 \\ x = \pm 2$
Bruker den positive verdien for x og finner at V(2) = 4. Siden alle mål var i dm. tilsvarer dette 4 liter.
Oppgave 5
a)
Ballen treffer bakken når y-koordinaten til posisjonsvektoren er null: $15-4,9t^2 =0 \\ t^2 = \frac{15}{4,9} \\t = \pm 1,75$
Den treffer bakken etter 1,75 sekunder.
b)
c)
For tegning av fartsvektor se figur i b. Fartsvektoren er den deriverte av posisjonsvektoren. Fartsvektoren blir da [3,9.8t] = [3, 7.84].
For å finne banefarten bruker vi Pytagoras og finner at den er $|v|=+ \sqrt{3^2+7,84^2} = 8,39 $.
Vinkelen til farten er: $tan \alpha = \frac{3}{7,84} \\ \alpha \approx 21^{\circ}$
Farten er 8,39 m/s og har en retning på ca 21 grader fra husveggen (loddlinjen eller vertikal akse).
d)
Tyngdens akselerasjon virker. Den er $9,81 m/s^2$, nedover, altså i y- retning. Dersom man deriverer fartsvektoren får man en x komponent lik null og en y komponent lik - 9,8 (fordi positiv retning er oppover og akselerasjonen er nedover.)
Oppgave 6
a)
$n^n \cdot ( \frac xn)^{lgx} = x^n \\ ( \frac xn)^{lgx} = ( \frac xn)^n \\ lg ( \frac xn)^{lgx} = lg ( \frac xn)^n$
b)
$ \lg ( \frac xn)^{\lg x} = \lg ( \frac xn)^n \\ \lg x( \lg x - \lg n) = n( \lg x - \lg n) \\ \lg x(\lg x - \lg n) - n(\lg x-\lg n)=0 \\ (\lg x - n)( \lg x - \lg n)=0$
c)
$lgx - n =0 \\ lgx =n \\ x= 10^n$
eller
$lgx - lgn = 0 \\ x = n$