S1 2014 høst LØSNING: Forskjell mellom sideversjoner
| (101 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 17: | Linje 17: | ||
==Oppgave 3== | ==Oppgave 3== | ||
<math> \left[ \begin{align*}2x =y - 4 \\ 4x^2+3y=12 \end{align*}\right] </math> | |||
<math> \left[ \begin{align*}y =2x + 4 \\ 4x^2+3(2x + 4) =12 \end{align*}\right] </math> | |||
Løser x av ligning to og får: | |||
$4x^2+6x+12 =12 \\ 4x^2+6x = 0 \\ x ( 4x+6) = 0 \\ x= 0 \vee x = - \frac 32$ | |||
Setter inn x verdier i ligning en og finner tilhørende y verdi: | |||
$ x= 0 \Rightarrow y = 4 , \quad x= - \frac 32 \Rightarrow y = 1 \\ x = 0 \wedge y=4 \quad \vee \quad x= - \frac 32 \wedge y=1 $ | |||
==Oppgave 4== | ==Oppgave 4== | ||
$lg(\frac{a^2}{b}) + lg(a^2b^2)- lg ( \frac ab) = | $\lg(\frac{a^2}{b}) + \lg(a^2b^2)- \lg ( \frac ab) = 2\lg a - \lg b +2\lg a +2\lg b -\lg b + \lg a = 5\lg a$ | ||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | ===a)=== | ||
$f(x) = - \frac 23x^3 + x^2 +2 \quad D_f =\R \\ f´(x) = -2x^2+2x = 2x( -x + 1)$ | |||
===b)=== | ===b)=== | ||
$f´(x) = 0 \\ 2x(-x+1)= 0 \\ x=0 \vee x =1$ | |||
f har ekstremalpunkter for x = 0, og for x = 1. For å finne ut hva som er maksimum og hva som er minimumspunkt kan vi tegne et fortegnsskjema. | |||
[[File:s1-2014h-5b.png]] | |||
$f(0) =2 \wedge f(1) = \frac 73$ | |||
Minimumspunkt: $ (0,2)$ | |||
Maksimumspunkt: $(1, \frac 73)$ | |||
===c)=== | ===c)=== | ||
$f(3) = - \frac23 3^3 +3^2 + 2 = -2 \cdot 9 + 9 + 2= -7$ | |||
Funksjonen er positiv for alle x verdier fra minus uendelig til et sted etter maksimumspunktet. Funksjonen har derfor bare ett nullpunkt, for x ett sted mellom 1 og 3. | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | ===a)=== | ||
Dersom man kan bruke en bokstav flere ganger, et det | Dersom man kan bruke en bokstav flere ganger, et det trekning med tilbakelegging: $4 \cdot 4 \cdot 4 = 4^3 = 64$ | ||
Det er mulig å lage 64 koder med fire bokstaver i tre posisjoner. | Det er mulig å lage 64 koder med fire bokstaver i tre posisjoner. | ||
| Linje 35: | Linje 66: | ||
===b)=== | ===b)=== | ||
Dersom en bokstav kun kan brukes en gang har vi | Dersom en bokstav kun kan brukes en gang har vi trekning uten tilbakelegging: $ 4 \cdot 3 \cdot 2= 24$ | ||
Det er mulig å lage 24 koder dersom en bokstav kun skal brukes en gang. | Det er mulig å lage 24 koder dersom en bokstav kun skal brukes en gang. | ||
| Linje 43: | Linje 74: | ||
Det er ofte mange måter å løse problemer på. Her er en: Vi skal lage en kode på tre bokstaver. Koden skal bestå av to eller tre like bokstaver. | Det er ofte mange måter å løse problemer på. Her er en: Vi skal lage en kode på tre bokstaver. Koden skal bestå av to eller tre like bokstaver. | ||
Dersom koden består av bare like bokstaver er det kun fire muligheter, fordi vi bare har fire bokstaver. | Dersom koden består av bare like bokstaver er det kun fire muligheter, fordi vi bare har fire forskjellige bokstaver. | ||
Dersom man har to like bokstaver kan disse arrangeres slik: | |||
$AAx \\ AxA \\xAA$ | |||
Der x er bokstavene B, C eller D. | |||
Man har fire mulige doble bokstaver, tre forskjellige posisjoner, og tre mulige valg av bokstaver etter de doble er trukket. Det gir | |||
$ 4 \cdot 3 \cdot 3 = 36 $ muligheter. Om man i tillegg tar med de fire mulighetene for tre like bokstaver, ser man at det er mulig å lage 40 forskjellige koder dersom hver av kodene skal inneholde minst to like bokstaver. | |||
Dette fant vi ut ved å tenke, uten hjelp fra svaret i deloppgave a og b. Litt lettere blir det dersom man ser at det svaret man er ute etter i c, denne oppgaven, er svaret i a minus svaret i b. | |||
Alle fire bokstaver kan brukes flere ganger - Hver bokstav kan bare brukes en gang = 64 - 24 = 40 | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | ===a)=== | ||
$E(x) = 4x +1200 + \frac{20000}{x}, \quad x > 0 \\E(200) = 4 \cdot 200 +1200 + \frac{20000}{200} \\ E(200) = 2100$ | |||
Dersom det produseres 200 enheter er enhetskostnaden kr. 2100,- | |||
De samlede produksjonskostnadene blir: | |||
$K(x)= 200 \cdot E(200) = 420.000$ | |||
Totale produksjonskostnader blir 420 000 kroner. | |||
===b)=== | ===b)=== | ||
Overskudd er inntekter minus kostnader. | |||
$O(x) = I(x) - K(x) \\ O(c) = 2000x - ( 4x^2+1200x + 20000) \\ O(x) = -4x^2 + 800x -20000 $ | |||
===c)=== | ===c)=== | ||
Vi deriverer overskuddsfunksjonen og setter den deriverte lik null, og finner x. ( Vi ser at dette er en parabel med et maksimum, siden det er negativt fortegn foran andregradsleddet.) | |||
$O´(x) = -8x + 800 \\ O´(x) = 0 \Rightarrow -8x + 800 = 0 \\ x = 100$ | |||
Produksjon av hundre enheter gir det største overskuddet, O(100) = 20000 kr. | |||
==Oppgave 8 == | ==Oppgave 8 == | ||
| Linje 55: | Linje 122: | ||
Vi har fasiten så da er det bare å gå i gang. Definisjonen på den deriverte er: | Vi har fasiten så da er det bare å gå i gang. Definisjonen på den deriverte er: | ||
$ f´(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} | $ f´(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} $ | ||
Vi får da: | |||
$ \lim_{\Delta x \to 0} \frac{((x + \Delta x)^3-(x+\Delta x)) - (x^3-x)}{\Delta x} \\ | |||
= \lim_{\Delta x \to 0} \frac{(x+ \Delta x) (x+ \Delta x)(x+ \Delta x) - (x +\Delta x) -(x^3-x)}{\Delta x} \\ | |||
= \lim_{\Delta x \to 0} \frac{(x^2+2x(\Delta x) + ( \Delta x)^2)(x+ \Delta x) - (x + \Delta x) - (x^3 - x)}{\Delta x} \\ | |||
= \lim_{ \Delta x \to 0} \frac{x^3+ 2x^2 \Delta x + x (\Delta x)^2 +x^2 \Delta x +2x( \Delta x)^2 + ( \Delta x)^3 - x - \Delta x - x^3 + x }{\Delta x} \\ | |||
= \lim_{ \Delta x \to 0} \frac{ \Delta x ( 3x^2 + 3x( \Delta x) + (\Delta x)^2-1) }{\Delta x} \\ | |||
= \lim_{ \Delta x \to 0} 3x^2 + 3x( \Delta x) + (\Delta x)^2-1 \\ | |||
= 3x^2-1$ | |||
Hvilket skulle vises. (Delta x går jo mot null, så de to midterste leddene bortfaller.) | |||
==DEL TO== | ==DEL TO== | ||
===Oppgave 1 === | |||
===a)=== | |||
[[File:s1-2014h-1a2.png]] | |||
Man observerer at den momentane vekstfarten i (2, f(2)) er lik den gjennomsnittlige vekstfarten i intervallet [1,3]. | |||
===b)=== | |||
$f ' (a)= 2a+3 \\ gjennomsnitt = \frac{f(a+1)-f(a-1)}{(a+1)-(a-1)} \\ \frac{(a+1)^2+3(a+1)-5 -( (a-1)^2+3(a-1)-5)}{2} \\ = \frac{a^2+2x+1+3a+3-5-a^2+2a-1-3a+3+5}{2} \\ = \frac{4a+6}{2} \\ = 2a+3$ | |||
Man får samme resultat som i a, men nå rent generelt for x = a. | |||
===Oppgave 2 === | |||
===a)=== | |||
På sparekonto i dag: | |||
$K(3)= 10000 \cdot 1,04^3 = 11248,64 $ kroner. | |||
===b)=== | |||
$K(t) = 25000 \\ 10000 \cdot 1,04^t =25000 \\ t \cdot lg 1,04 = lg 2,5 \\ t = 23, 36$ | |||
Det vil ta ca. 23, 5 år før beløpet har vokst til 25000 kroner. | |||
===c)=== | |||
$x \cdot 1,04^7 = 25000 \\ x = \frac{25000}{1,04^7}x = 18997,95$ | |||
Beløpet som må stå inne i dag, for at han skal få 25000 kroner på konto om syv år er 18997,95 kroner. Han ha allerede 11248,64 kroner og må derfor sette inn 7749,31 kroner. | |||
==Oppgave 3== | |||
===a)=== | |||
$P(X=3)= \binom{10}{3} 0,4^3 \cdot (0,6)^{7} = 0,215 = 21,5$ % | |||
Det er 21,5% sannsynlig at bussen stopper ved tre holdeplasser, dvs. at den bruker 23 minutter på turen. | |||
===b)=== | |||
[[File:s1-h2014-3b.png]] | |||
Det er 63,3% sannsynlig at bussturen tar mindre enn 25 minutter. | |||
===c)=== | |||
Her har man en hypergeometrisk situasjon. | |||
[[File:s1-h2014-3c.png]] | |||
Det er 53,8 % sannsynlig at minst en sniker blir tatt. | |||
==Oppgave 4== | |||
===a)=== | |||
[[File:s1-h2014-4b.png]] | |||
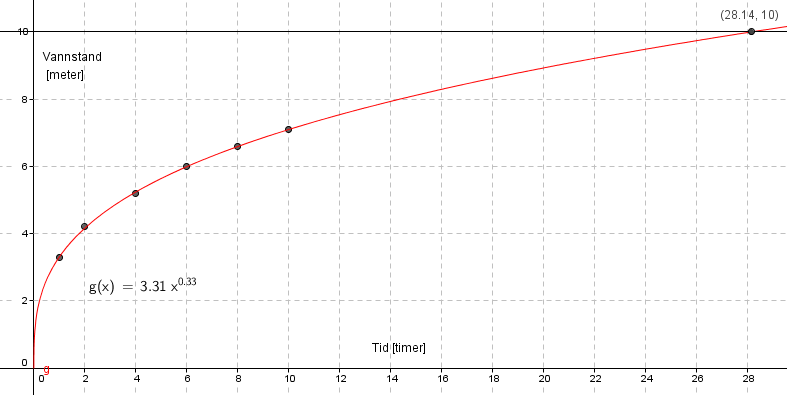
$g(x)= 3,31 \cdot x^{0,33}$ er en potensfunksjon sm passer til tallene i tabellen. | |||
===b)=== | |||
Fra figuren i a) ser man at det vil ta 28,14 timer, før tanken er full. Det tilsvare i overkant av 28 timer og 8 minutter. Vi kjenner ikke radius av kjeglens grunnflate og må derfor gå veien om vannmengde per time for å finne det totale volumet: | |||
$V = 18 m^3 /time \cdot 28,14 timer = 506,52 m^3$ | |||
===c)=== | |||
Ny tank skal romme 1000 $m^3$ og ha samme form som den gamle tanken. | |||
Radius i gammel tank: | |||
$r = \sqrt{\frac{3V}{\pi \cdot h}} \approx 6,95 m$ | |||
Forholdet mellom høyde og radius i gammel tank er $\frac hr = 1,44$. Forholdet skal være det samme i ny tank, siden formen skal være den samme: | |||
$V= \frac 13 \pi r^2 \cdot 1,44 r \Rightarrow r= \sqrt[3]{\frac{3V}{1,44 \pi}} = 8,72m$ | |||
Høyden i den nye tanken er $h = 1,44 r = 12,56 m$ | |||
Pumpen pumper 18 $m^3$ per time. Den bruker: $\frac{1000 m^3}{18 m^3/time} = 55,56 timer$, som tilsvarer ca. 55 timer og 34 minutter. | |||
==Oppgave 5== | |||
===a)=== | |||
[[File:s1-2014H-5b.png]] | |||
Bilene møtes i s, som er avstanden fra A. Da har bil A kjørt i 60 km/t i t antall timer. Bilen i B må kjøre motsatt vei og starter 20 minutter senere. Bil B kjører mot A i 40 km/t og det gjør den i (t - 1/3) timer. | |||
===b)=== | |||
<math> \left[ \begin{align*} s=60 \cdot t \\ s= 200 - 40 (t- \frac 13) \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} s=60 \cdot t \\ 60 \cdot t = 200 - 40 (t- \frac 13) \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} s=60 \cdot t \\ 100 \cdot t = 200 + \frac {40}{3} \end{align*}\right] </math> | |||
t = 2,133 timer som er ca. 2 timer og 8 minutter. | |||
Bilene møtes i s, som er ca. 128 kilometer fra A. | |||
===c)=== | |||
Dersom bilene skal møtes midt mellom A og B, vil bil A bruke $t= \frac{100}{60} = \frac 53$ timer. | |||
Bil B: $100 = 200 -v(\frac 53- \frac 13) \\ \frac 43v = 100 \\v = 75 km/t$ | |||
Bil B må holde en hastighet på 75 kilometer per time for at de skal møtes på midten. | |||
==Oppgave 6== | |||
===a)=== | |||
$8x + 4y = 900 \\ y = 225 + 2x $ | |||
Volum av prisme: | |||
$ V(x,y)= x^2y \\ | |||
V(x) = x^2(225-2x) \\ | |||
V(x)= -2x^3+225x^2$ | |||
Som skulle vises. | |||
===b)=== | |||
$V ' (x) = -6x^2 + 450x \\ V'(x)=0 \\ -6x^2+450x=0 \\ x=0 \vee x= 75$ | |||
Størst volum får pakken når x= 75 centimeter. Da er $y= 225 - 2 \cdot 75 = 75 $ cm. Man ser at volumet av pakken blir størst når alle sidene i prismet er like lange. | |||
==Oppgave 7== | |||
===a)=== | |||
$x \geq 0 \wedge y \geq 0$ : Man kan ikke produsere mindre enn null kg av noen av typene. | |||
$0,60x + 0,20y \leq 800$ , er begrensningen på mel. | |||
$0,40x + 0,80 y \leq 1000$ , er begrensningen på kjøttdeig. | |||
===b)=== | |||
[[File:s1-2014h-7bc.png]] | |||
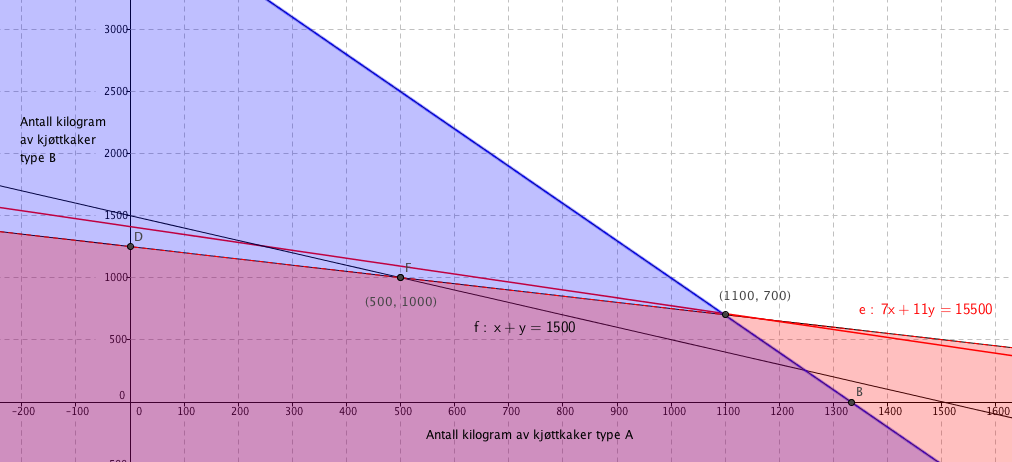
Inntektene blir størst om de produserer 1100 kg av type A og 700 kg av type B. Inntektene blir da: | |||
$70 \cdot 1100 + 110 \cdot 700 = 154000$ kroner. | |||
===c)=== | |||
Dersom de kun har kapasitet til å produsere 1500 kg, har man at x + y = 1500 (se linje i figur over). Den optimale produksjonen blir da 500 kg av A og 1000 kg av B. Inntektene blir da 145000 kroner. | |||
Siste sideversjon per 30. mar. 2015 kl. 04:23
DEL EN
Oppgave 1
a)
$2x -10 = x(x-5) \\ -x^2+7x-10 =0 \\ x= \frac{-7 \pm \sqrt{49- 4 \cdot(-1) \cdot (-10)}}{-2} \\x= \frac{-7\pm 3}{-2} \\ x= 2 \vee x = 5$
b)
$lg(\frac x2) + 3 =5 \\ lg( \frac x2) = 2 \\10^{lg( \frac x2)} = 10^2 \\ \frac x2 = 100 \\ x= 200 $
Oppgave 2
$995 \cdot 995 = (1000 -5)^2 = 1000000-2\cdot 5 \cdot 1000 + 25 = 990025$
Oppgave 3
<math> \left[ \begin{align*}2x =y - 4 \\ 4x^2+3y=12 \end{align*}\right] </math>
<math> \left[ \begin{align*}y =2x + 4 \\ 4x^2+3(2x + 4) =12 \end{align*}\right] </math>
Løser x av ligning to og får:
$4x^2+6x+12 =12 \\ 4x^2+6x = 0 \\ x ( 4x+6) = 0 \\ x= 0 \vee x = - \frac 32$
Setter inn x verdier i ligning en og finner tilhørende y verdi:
$ x= 0 \Rightarrow y = 4 , \quad x= - \frac 32 \Rightarrow y = 1 \\ x = 0 \wedge y=4 \quad \vee \quad x= - \frac 32 \wedge y=1 $
Oppgave 4
$\lg(\frac{a^2}{b}) + \lg(a^2b^2)- \lg ( \frac ab) = 2\lg a - \lg b +2\lg a +2\lg b -\lg b + \lg a = 5\lg a$
Oppgave 5
a)
$f(x) = - \frac 23x^3 + x^2 +2 \quad D_f =\R \\ f´(x) = -2x^2+2x = 2x( -x + 1)$
b)
$f´(x) = 0 \\ 2x(-x+1)= 0 \\ x=0 \vee x =1$
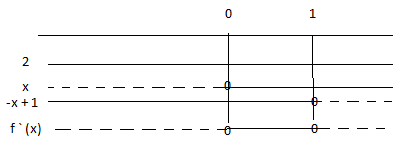
f har ekstremalpunkter for x = 0, og for x = 1. For å finne ut hva som er maksimum og hva som er minimumspunkt kan vi tegne et fortegnsskjema.
$f(0) =2 \wedge f(1) = \frac 73$
Minimumspunkt: $ (0,2)$
Maksimumspunkt: $(1, \frac 73)$
c)
$f(3) = - \frac23 3^3 +3^2 + 2 = -2 \cdot 9 + 9 + 2= -7$
Funksjonen er positiv for alle x verdier fra minus uendelig til et sted etter maksimumspunktet. Funksjonen har derfor bare ett nullpunkt, for x ett sted mellom 1 og 3.
Oppgave 6
a)
Dersom man kan bruke en bokstav flere ganger, et det trekning med tilbakelegging: $4 \cdot 4 \cdot 4 = 4^3 = 64$
Det er mulig å lage 64 koder med fire bokstaver i tre posisjoner.
b)
Dersom en bokstav kun kan brukes en gang har vi trekning uten tilbakelegging: $ 4 \cdot 3 \cdot 2= 24$
Det er mulig å lage 24 koder dersom en bokstav kun skal brukes en gang.
c)
Det er ofte mange måter å løse problemer på. Her er en: Vi skal lage en kode på tre bokstaver. Koden skal bestå av to eller tre like bokstaver.
Dersom koden består av bare like bokstaver er det kun fire muligheter, fordi vi bare har fire forskjellige bokstaver.
Dersom man har to like bokstaver kan disse arrangeres slik:
$AAx \\ AxA \\xAA$ Der x er bokstavene B, C eller D.
Man har fire mulige doble bokstaver, tre forskjellige posisjoner, og tre mulige valg av bokstaver etter de doble er trukket. Det gir
$ 4 \cdot 3 \cdot 3 = 36 $ muligheter. Om man i tillegg tar med de fire mulighetene for tre like bokstaver, ser man at det er mulig å lage 40 forskjellige koder dersom hver av kodene skal inneholde minst to like bokstaver.
Dette fant vi ut ved å tenke, uten hjelp fra svaret i deloppgave a og b. Litt lettere blir det dersom man ser at det svaret man er ute etter i c, denne oppgaven, er svaret i a minus svaret i b.
Alle fire bokstaver kan brukes flere ganger - Hver bokstav kan bare brukes en gang = 64 - 24 = 40
Oppgave 7
a)
$E(x) = 4x +1200 + \frac{20000}{x}, \quad x > 0 \\E(200) = 4 \cdot 200 +1200 + \frac{20000}{200} \\ E(200) = 2100$
Dersom det produseres 200 enheter er enhetskostnaden kr. 2100,-
De samlede produksjonskostnadene blir:
$K(x)= 200 \cdot E(200) = 420.000$
Totale produksjonskostnader blir 420 000 kroner.
b)
Overskudd er inntekter minus kostnader.
$O(x) = I(x) - K(x) \\ O(c) = 2000x - ( 4x^2+1200x + 20000) \\ O(x) = -4x^2 + 800x -20000 $
c)
Vi deriverer overskuddsfunksjonen og setter den deriverte lik null, og finner x. ( Vi ser at dette er en parabel med et maksimum, siden det er negativt fortegn foran andregradsleddet.)
$O´(x) = -8x + 800 \\ O´(x) = 0 \Rightarrow -8x + 800 = 0 \\ x = 100$
Produksjon av hundre enheter gir det største overskuddet, O(100) = 20000 kr.
Oppgave 8
$f(x) = x^3-x \\ f´(x)=3x^2-1$
Vi har fasiten så da er det bare å gå i gang. Definisjonen på den deriverte er:
$ f´(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} $
Vi får da:
$ \lim_{\Delta x \to 0} \frac{((x + \Delta x)^3-(x+\Delta x)) - (x^3-x)}{\Delta x} \\ = \lim_{\Delta x \to 0} \frac{(x+ \Delta x) (x+ \Delta x)(x+ \Delta x) - (x +\Delta x) -(x^3-x)}{\Delta x} \\ = \lim_{\Delta x \to 0} \frac{(x^2+2x(\Delta x) + ( \Delta x)^2)(x+ \Delta x) - (x + \Delta x) - (x^3 - x)}{\Delta x} \\ = \lim_{ \Delta x \to 0} \frac{x^3+ 2x^2 \Delta x + x (\Delta x)^2 +x^2 \Delta x +2x( \Delta x)^2 + ( \Delta x)^3 - x - \Delta x - x^3 + x }{\Delta x} \\ = \lim_{ \Delta x \to 0} \frac{ \Delta x ( 3x^2 + 3x( \Delta x) + (\Delta x)^2-1) }{\Delta x} \\ = \lim_{ \Delta x \to 0} 3x^2 + 3x( \Delta x) + (\Delta x)^2-1 \\ = 3x^2-1$
Hvilket skulle vises. (Delta x går jo mot null, så de to midterste leddene bortfaller.)
DEL TO
Oppgave 1
a)
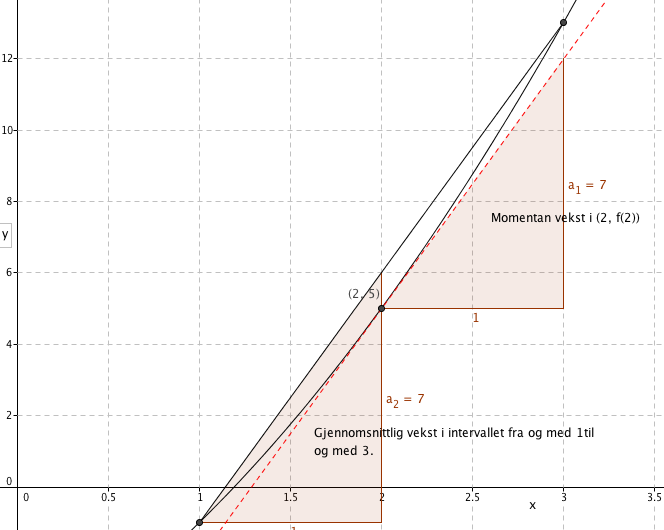
Man observerer at den momentane vekstfarten i (2, f(2)) er lik den gjennomsnittlige vekstfarten i intervallet [1,3].
b)
$f ' (a)= 2a+3 \\ gjennomsnitt = \frac{f(a+1)-f(a-1)}{(a+1)-(a-1)} \\ \frac{(a+1)^2+3(a+1)-5 -( (a-1)^2+3(a-1)-5)}{2} \\ = \frac{a^2+2x+1+3a+3-5-a^2+2a-1-3a+3+5}{2} \\ = \frac{4a+6}{2} \\ = 2a+3$
Man får samme resultat som i a, men nå rent generelt for x = a.
Oppgave 2
a)
På sparekonto i dag:
$K(3)= 10000 \cdot 1,04^3 = 11248,64 $ kroner.
b)
$K(t) = 25000 \\ 10000 \cdot 1,04^t =25000 \\ t \cdot lg 1,04 = lg 2,5 \\ t = 23, 36$
Det vil ta ca. 23, 5 år før beløpet har vokst til 25000 kroner.
c)
$x \cdot 1,04^7 = 25000 \\ x = \frac{25000}{1,04^7}x = 18997,95$
Beløpet som må stå inne i dag, for at han skal få 25000 kroner på konto om syv år er 18997,95 kroner. Han ha allerede 11248,64 kroner og må derfor sette inn 7749,31 kroner.
Oppgave 3
a)
$P(X=3)= \binom{10}{3} 0,4^3 \cdot (0,6)^{7} = 0,215 = 21,5$ %
Det er 21,5% sannsynlig at bussen stopper ved tre holdeplasser, dvs. at den bruker 23 minutter på turen.
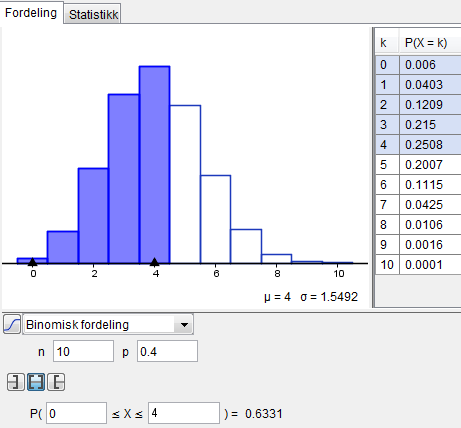
b)
Det er 63,3% sannsynlig at bussturen tar mindre enn 25 minutter.
c)
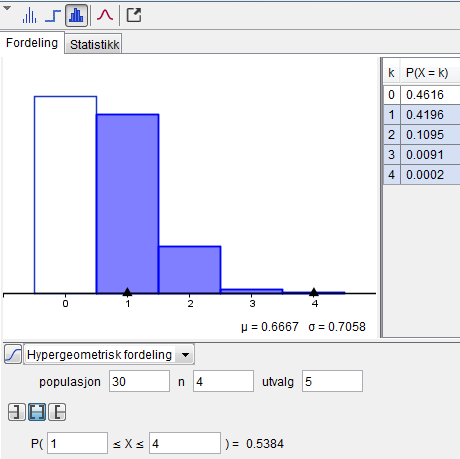
Her har man en hypergeometrisk situasjon.
Det er 53,8 % sannsynlig at minst en sniker blir tatt.
Oppgave 4
a)
$g(x)= 3,31 \cdot x^{0,33}$ er en potensfunksjon sm passer til tallene i tabellen.
b)
Fra figuren i a) ser man at det vil ta 28,14 timer, før tanken er full. Det tilsvare i overkant av 28 timer og 8 minutter. Vi kjenner ikke radius av kjeglens grunnflate og må derfor gå veien om vannmengde per time for å finne det totale volumet:
$V = 18 m^3 /time \cdot 28,14 timer = 506,52 m^3$
c)
Ny tank skal romme 1000 $m^3$ og ha samme form som den gamle tanken.
Radius i gammel tank:
$r = \sqrt{\frac{3V}{\pi \cdot h}} \approx 6,95 m$
Forholdet mellom høyde og radius i gammel tank er $\frac hr = 1,44$. Forholdet skal være det samme i ny tank, siden formen skal være den samme:
$V= \frac 13 \pi r^2 \cdot 1,44 r \Rightarrow r= \sqrt[3]{\frac{3V}{1,44 \pi}} = 8,72m$
Høyden i den nye tanken er $h = 1,44 r = 12,56 m$
Pumpen pumper 18 $m^3$ per time. Den bruker: $\frac{1000 m^3}{18 m^3/time} = 55,56 timer$, som tilsvarer ca. 55 timer og 34 minutter.
Oppgave 5
a)
Bilene møtes i s, som er avstanden fra A. Da har bil A kjørt i 60 km/t i t antall timer. Bilen i B må kjøre motsatt vei og starter 20 minutter senere. Bil B kjører mot A i 40 km/t og det gjør den i (t - 1/3) timer.
b)
<math> \left[ \begin{align*} s=60 \cdot t \\ s= 200 - 40 (t- \frac 13) \end{align*}\right] </math>
<math> \left[ \begin{align*} s=60 \cdot t \\ 60 \cdot t = 200 - 40 (t- \frac 13) \end{align*}\right] </math>
<math> \left[ \begin{align*} s=60 \cdot t \\ 100 \cdot t = 200 + \frac {40}{3} \end{align*}\right] </math>
t = 2,133 timer som er ca. 2 timer og 8 minutter.
Bilene møtes i s, som er ca. 128 kilometer fra A.
c)
Dersom bilene skal møtes midt mellom A og B, vil bil A bruke $t= \frac{100}{60} = \frac 53$ timer.
Bil B: $100 = 200 -v(\frac 53- \frac 13) \\ \frac 43v = 100 \\v = 75 km/t$
Bil B må holde en hastighet på 75 kilometer per time for at de skal møtes på midten.
Oppgave 6
a)
$8x + 4y = 900 \\ y = 225 + 2x $
Volum av prisme:
$ V(x,y)= x^2y \\ V(x) = x^2(225-2x) \\ V(x)= -2x^3+225x^2$
Som skulle vises.
b)
$V ' (x) = -6x^2 + 450x \\ V'(x)=0 \\ -6x^2+450x=0 \\ x=0 \vee x= 75$
Størst volum får pakken når x= 75 centimeter. Da er $y= 225 - 2 \cdot 75 = 75 $ cm. Man ser at volumet av pakken blir størst når alle sidene i prismet er like lange.
Oppgave 7
a)
$x \geq 0 \wedge y \geq 0$ : Man kan ikke produsere mindre enn null kg av noen av typene.
$0,60x + 0,20y \leq 800$ , er begrensningen på mel.
$0,40x + 0,80 y \leq 1000$ , er begrensningen på kjøttdeig.
b)
Inntektene blir størst om de produserer 1100 kg av type A og 700 kg av type B. Inntektene blir da:
$70 \cdot 1100 + 110 \cdot 700 = 154000$ kroner.
c)
Dersom de kun har kapasitet til å produsere 1500 kg, har man at x + y = 1500 (se linje i figur over). Den optimale produksjonen blir da 500 kg av A og 1000 kg av B. Inntektene blir da 145000 kroner.