1T 2014 vår LØSNING: Forskjell mellom sideversjoner
m Teksterstatting – «/ressurser/eksamen/» til «/res/eksamen/» |
|||
| (52 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://matematikk.net/ | [http://matematikk.net/res/eksamen/1T/1T_V14.pdf Oppgaven som pdf] | ||
[http://matematikk.net/matteprat/viewtopic.php?f=13&t=37463 Tråd om denne oppgaven på Matteprat] | [http://matematikk.net/matteprat/viewtopic.php?f=13&t=37463 Tråd om denne oppgaven på Matteprat] | ||
| Linje 33: | Linje 33: | ||
==Oppgave 5:== | ==Oppgave 5:== | ||
<math> \left[ \begin{align*}2x-3y=-7 \\ 3x-y=7 \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} y=3x-7 \\ 2x -3(3x-7) = -7] \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} 2x-9x + 21 = -7 \\ - 7x = - 28 \\ x= 4 \end{align*}\right] </math> | |||
<math> \left[ \begin{align*} 3x-y=7 \\ 12 - y =7\\ y=5 \end{align*}\right] </math> | |||
$ x = 4 \wedge y = 5$ | |||
==Oppgave 6:== | ==Oppgave 6:== | ||
| Linje 51: | Linje 59: | ||
==Oppgave 8:== | ==Oppgave 8:== | ||
[[File:8-1T-del1-2014.png]] | |||
===1)=== | |||
$AB= \sqrt{100 - 49} = \sqrt{51}$ | |||
AB er altså litt lengre enn 7 enheter. Dersom AB hadde vært syv enheter ville arealet vært 24,5, altså er det nå litt større enn 24,5. Påstanden er riktig. | |||
===2)=== | |||
$sin A = \frac{7}{10} \\ cos A = \frac{\sqrt{51}}{10}$ | |||
Påstanden er feil. | |||
==Oppgave 9:== | ==Oppgave 9:== | ||
| Linje 94: | Linje 117: | ||
===a)=== | ===a)=== | ||
[[File:1t-14-1abc.png]] | |||
Bruker Geogebra og finner at den lineære funksjonen som passer best med de oppgitte data er : | |||
y = 0,83x + 2,31 | |||
x er antall uker etter treningsstart. | |||
===b)=== | ===b)=== | ||
Avlesning av grafen i a gir ca. 23 km. | |||
===c)=== | ===c)=== | ||
Avlesning av grafen i a viser at det skjer den niende treningsuken. | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | ===a)=== | ||
[[File:opg1a-14vt.png]] | |||
===b)=== | ===b)=== | ||
$f(x)=0,0017x^3-0,13x^2+2,3x+72$ | |||
Fra funksjonsuttrykket ser man at f (0) = 72. Dvs. han veide 72 kg. den 1. jan 2013. | |||
===c)=== | ===c)=== | ||
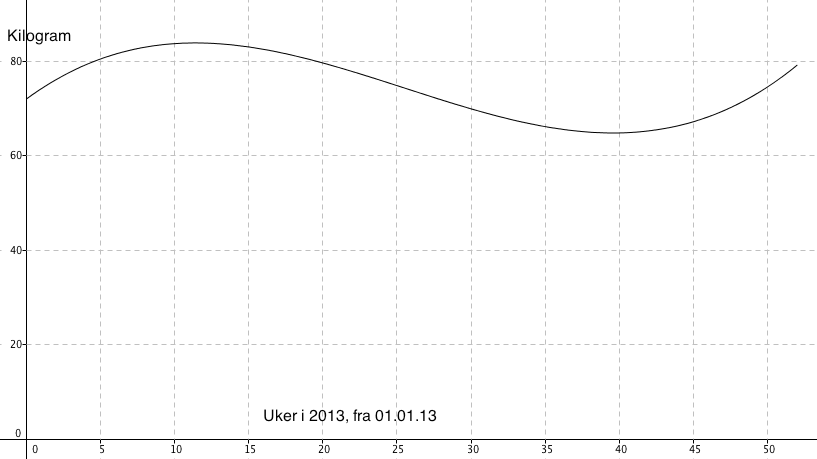
[[File:opg1b-14vt.png]] | |||
Fra figuren der man at han veide over 70 kg. fra uke 1 til 30 og fra uke 47 til 52, altså ca. 35 uker av året. | |||
===d)=== | ===d)=== | ||
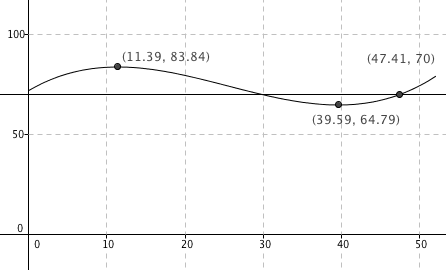
Fra Figuren i c ser man at han veide mest i uke 11, nesten 84 kg. Han veide minst i uke 39, da i underkant av 65 kg. Dersom man forholder seg til tallene over er det et vekttap på 19kg. over 28 uker. Det gir et vekttap på ca. 680 gram per uke. | |||
===e)=== | ===e)=== | ||
f'(3) = 1,57 | |||
f'(25) = -1,01 | |||
Har brukt Geogebra. Du kan også derivere for hånd, for så å sette inn 3 og 25 i argumentet. Det krever noe regning og tar trolig lengre tid. | |||
Svarene gir oss den momentane vektendringen i uke 3 og i uke 25. | |||
==Oppgave 3== | |||
===a)=== | |||
{| width="auto" | |||
| | |||
|Type 1 | |||
|Type 2 | |||
|Total | |||
|- | |||
|Feil | |||
|100 | |||
|600 | |||
|700 | |||
|- | |||
|Ikke feil | |||
|900 | |||
|3400 | |||
|4300 | |||
|- | |||
|Total | |||
|1000 | |||
|4000 | |||
|5000 | |||
|} | |||
===b)=== | |||
Det er 700 "mulige" for feil. En av hver type kan trekkes på to måter. Det gunstige resultatet, en av hver, kan man få ved å trekke type en først, og så type to, eller ved å trekke type to først, og så type en. | |||
Sannsynligheten for en av hver, gitt feil blir: | |||
$P( en \quad av \quad hver | feil) = 2 \cdot \frac{100}{700} \cdot \frac{600}{699} = 0,245$ | |||
Dvs. det er 24,5% sannsynlig at man har en av hver type, når man vet at begge er defekte. | |||
==Oppgave 4== | |||
'''a)''' | |||
H: Trekker hvit kule | |||
R: Trekker rød kule | |||
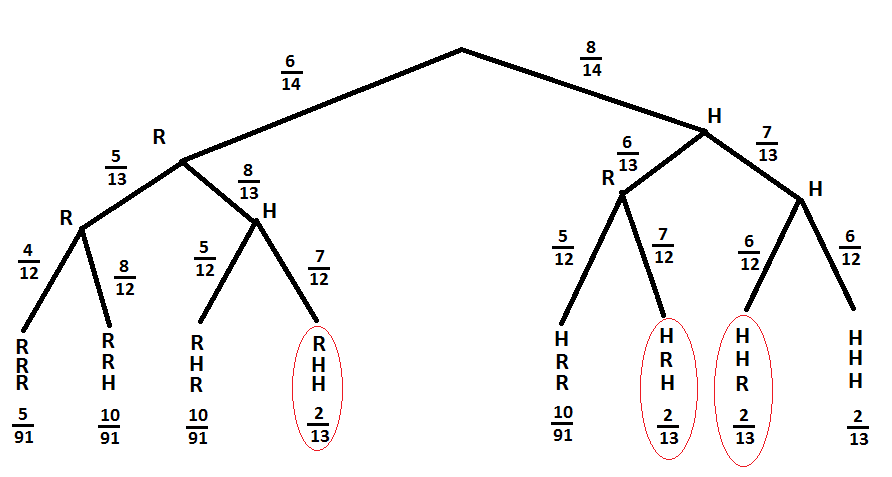
[[Fil:1PV2014del2oppg2a.png]] | |||
'''b)''' | |||
P(to hvite og én rød) = $P(R, H, H) + P(H, R, H) + P(H, H, R) = 3 \cdot \frac{2}{13}= \frac{6}{13}$ | |||
==Oppgave 5== | |||
De to delene som skal være like lange har lengde x. Vi har da 2x. | |||
Den tredje delen er dobbelt så lang som de to like, til sammen, altså er del tre lik 4x. | |||
Del fire er dobbelt så lang som del tre, altså 8x. | |||
Vi får da: | |||
$2x + 4x + 8 x = 35cm \\ 14x= 35cm \\ x = 2,5 cm$ | |||
De to like stykkene er 2,5 cm hver. Det tredje stykket er 10 cm. Det fjerde stykket er 20 cm. | |||
==Oppgave 6== | |||
Vi må først finne en vinkel. Til det bruker vi cosinussetningen. Når vi har en vinkel kan vi bruke arealsetningen. | |||
$a^2=b^2+c^2-2bcCosA \\ CosA = \frac{a^2-b^2-c^2}{-2bc} = \frac{5^2-4^2-8^2}{-2 \cdot 4 \cdot8} = \frac{-55}{-64}$ | |||
Vinkel A er 30,75 grader. | |||
Arealsetning: | |||
$A = \frac 12 bc SinA = \frac 12 \cdot 4 \cdot 8 \cdot sin 30,75 = 8,2$ | |||
== Oppgave 7== | |||
===a)=== | |||
$AB = 3,0 \cdot cos 52^{\circ} = 1,85$ | |||
Båten ligger 1,85 meter fra brygga. | |||
===b)=== | |||
Ny vannstand: | |||
$AC = 3,0 \cdot sin 52^{\circ} + 0,30 m = 2,66 m $ | |||
Bruker Pytagoras og finner ny avstand mellom båt og brygge: | |||
$AB = \sqrt{3^2 - 2,66^2} = 1,40 $ | |||
Båten ligger nå 1,40 meter fra brygga. | |||
==Oppgave 8== | |||
===a)=== | |||
Omkretsen er summen av de tre sidene. | |||
AB = 8 | |||
$BC = \sqrt{x^2 + 36}$ (pytagoras) | |||
$AC = \sqrt{(8-x)^2 +36} = \sqrt{64-16x +x^2 + 36} = \sqrt{x^2-16x+100}$ | |||
Dersom man legger sammen disse tre uttrykkene får man omkretsfunksjonen f, slik den er gitt i oppgaven: | |||
$f(x) = AB + BC + AC = 8 +\sqrt{x^2 + 36} +\sqrt{x^2-16x+100}$ | |||
x må ligge mellom 0 og 8 fordi AB = 8. | |||
===b)=== | |||
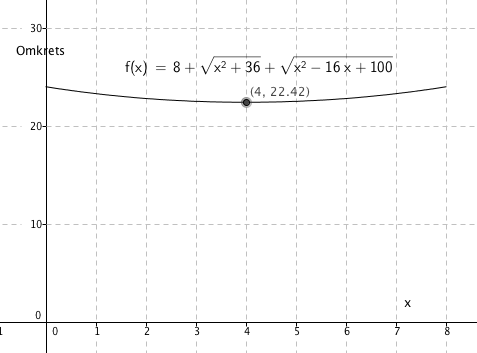
[[File:1t-08-del2-vol2.png]] | |||
Den minste omkretsen får man når x=4 (Geogebra, ekstremalpunkt). Man observerer at det er midtpunktet på AB. AC og BC vil være like lange, trekanten er da likebeint. Når x = 4 er omkretsen 22,42. | |||
==Oppgave 9== | |||
Han "flipper" først trekantene ADC og DBC på linjestykket AB. Så speilvender han trekanten DBE om linjestykket AB. Punktene F og G har samme avstand (6) fra linjestykket AB. I planet er den korteste vei mellom to punkter en rett linje. Han trekker denne. Den skjærer linjestykket AB i D´. I D´ har vi toppvinkler. I tillegg er vinkel A og B begge 90 grader. Vinklene i trekantene AD´F og GBD´er derfor like. Det er også sidene AF og GB. Av det kan man slutte at disse to trekantene er kongruente, og Petter har rett. | |||
Siste sideversjon per 19. okt. 2014 kl. 17:06
Tråd om denne oppgaven på Matteprat
Enda en tråd om denne oppgaven på Matteprat
DEL EN
Oppgave 1:
$2,5 \cdot 10^{15} \cdot 3,0 \cdot 10^{-5} = 7,5 \cdot 10^{15+(-5)} = 7,5 \cdot 10^{10}$
Oppgave 2:
$9^{ \frac12}\cdot 6^0 \cdot 4^{-1} \cdot \sqrt[3]{8^2} = \\ (3^2)^{\frac12} \cdot 1 \cdot \frac 14 \cdot \sqrt[3]{2^6} = \\ \frac34 \cdot 2^2 = 3$
Oppgave 3:
$2^{2-x} \cdot 2^{1+2x} =32 \\ 2^{2-x+1+2x} = 2^5 \\ 3+x=5 \\ x=2$
Oppgave 4:
$x^2 +8x +c \\$ Vi har at $a^2 +2ab +b^2 = (a+b)^2$
Dvs: c = $4^2 = 16$
Oppgave 5:
<math> \left[ \begin{align*}2x-3y=-7 \\ 3x-y=7 \end{align*}\right] </math>
<math> \left[ \begin{align*} y=3x-7 \\ 2x -3(3x-7) = -7] \end{align*}\right] </math>
<math> \left[ \begin{align*} 2x-9x + 21 = -7 \\ - 7x = - 28 \\ x= 4 \end{align*}\right] </math>
<math> \left[ \begin{align*} 3x-y=7 \\ 12 - y =7\\ y=5 \end{align*}\right] </math>
$ x = 4 \wedge y = 5$
Oppgave 6:
$\frac {6}{x-3} - \frac {5x+15}{x^2-9}+ 1= \\ \frac{6}{x-3} - \frac {5(x+3)}{(x+3)(x-3)}+ \frac {x-3}{x-3} = \\ \frac {6-5+ x - 3 }{x-3}= \\ \frac {x-2}{x-3}$
Oppgave 7:
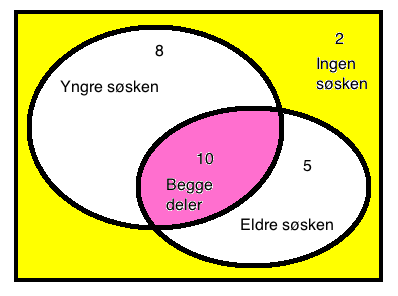
a)
b)
P(eldre men ikke yngre søsken) = $ \frac {5}{25} = \frac 15$
c)
P(yngre søsken gitt eldere søsken) = $\frac {10}{15}= \frac{2}{3}$
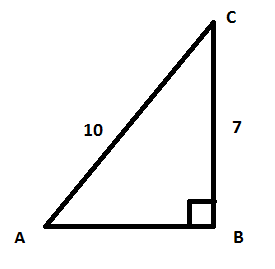
Oppgave 8:
1)
$AB= \sqrt{100 - 49} = \sqrt{51}$
AB er altså litt lengre enn 7 enheter. Dersom AB hadde vært syv enheter ville arealet vært 24,5, altså er det nå litt større enn 24,5. Påstanden er riktig.
2)
$sin A = \frac{7}{10} \\ cos A = \frac{\sqrt{51}}{10}$
Påstanden er feil.
Oppgave 9:
$f(x)= x^2+2x-3$
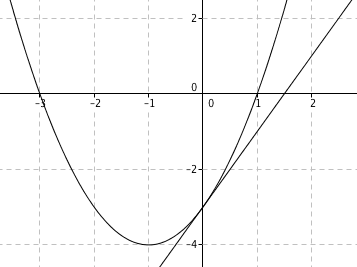
a)
Nullpunkt: $f(x)=0 \\ x^2+2x-3 = 0 \\ x= \frac{-2 \pm \sqrt{4-4 \cdot (-3)}}{2} \\ x= \frac{-2 \pm 4}{2} \\x= -3 \vee x= 1$
Nullpunktene er (-3, 0 ) og (1, 0).
b)
$f´(x) = 2x+2 \\f´(x)=2 \Rightarrow x = 0 $
Tangeringspunkt. ( 0 , f(0) ) som er (0, -3)
Likning for tangenten:
$y = ax+b \\ -3 = 2 \cdot 0 -3 \\ b = -3 \\ y=2x-3$
Den siste utregningen kunne vi sløyfet i dette tilfellet, siden vi vet at tangeringen skjer på y aksen (x = 0).
c)
Dette er del en, så du må tegne for hånd. Lag verditabell. Du må også markere hva som er x-akse og y-akse.
Oppgave 10:
$f(x) = x^2+bx+c $
Grafen skjærer y - aksen i (0, 4), dvs. f(0) = 4, altså er c = 4.
Funksjonen f har ett nullpunkt, dvs: $ b^2 - 4ac = 0 \\ b= \pm 4 \\ f(x)= x^2-4x+ 4 \vee f(x)= x^2+ 4x+ 4 $
DEL TO
Oppgave 1
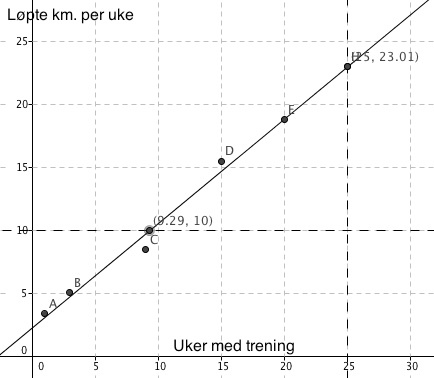
a)
Bruker Geogebra og finner at den lineære funksjonen som passer best med de oppgitte data er :
y = 0,83x + 2,31
x er antall uker etter treningsstart.
b)
Avlesning av grafen i a gir ca. 23 km.
c)
Avlesning av grafen i a viser at det skjer den niende treningsuken.
Oppgave 2
a)
b)
$f(x)=0,0017x^3-0,13x^2+2,3x+72$
Fra funksjonsuttrykket ser man at f (0) = 72. Dvs. han veide 72 kg. den 1. jan 2013.
c)
Fra figuren der man at han veide over 70 kg. fra uke 1 til 30 og fra uke 47 til 52, altså ca. 35 uker av året.
d)
Fra Figuren i c ser man at han veide mest i uke 11, nesten 84 kg. Han veide minst i uke 39, da i underkant av 65 kg. Dersom man forholder seg til tallene over er det et vekttap på 19kg. over 28 uker. Det gir et vekttap på ca. 680 gram per uke.
e)
f'(3) = 1,57 f'(25) = -1,01
Har brukt Geogebra. Du kan også derivere for hånd, for så å sette inn 3 og 25 i argumentet. Det krever noe regning og tar trolig lengre tid.
Svarene gir oss den momentane vektendringen i uke 3 og i uke 25.
Oppgave 3
a)
| Type 1 | Type 2 | Total | |
| Feil | 100 | 600 | 700 |
| Ikke feil | 900 | 3400 | 4300 |
| Total | 1000 | 4000 | 5000 |
b)
Det er 700 "mulige" for feil. En av hver type kan trekkes på to måter. Det gunstige resultatet, en av hver, kan man få ved å trekke type en først, og så type to, eller ved å trekke type to først, og så type en.
Sannsynligheten for en av hver, gitt feil blir:
$P( en \quad av \quad hver | feil) = 2 \cdot \frac{100}{700} \cdot \frac{600}{699} = 0,245$
Dvs. det er 24,5% sannsynlig at man har en av hver type, når man vet at begge er defekte.
Oppgave 4
a)
H: Trekker hvit kule
R: Trekker rød kule
b) P(to hvite og én rød) = $P(R, H, H) + P(H, R, H) + P(H, H, R) = 3 \cdot \frac{2}{13}= \frac{6}{13}$
Oppgave 5
De to delene som skal være like lange har lengde x. Vi har da 2x. Den tredje delen er dobbelt så lang som de to like, til sammen, altså er del tre lik 4x. Del fire er dobbelt så lang som del tre, altså 8x.
Vi får da:
$2x + 4x + 8 x = 35cm \\ 14x= 35cm \\ x = 2,5 cm$
De to like stykkene er 2,5 cm hver. Det tredje stykket er 10 cm. Det fjerde stykket er 20 cm.
Oppgave 6
Vi må først finne en vinkel. Til det bruker vi cosinussetningen. Når vi har en vinkel kan vi bruke arealsetningen.
$a^2=b^2+c^2-2bcCosA \\ CosA = \frac{a^2-b^2-c^2}{-2bc} = \frac{5^2-4^2-8^2}{-2 \cdot 4 \cdot8} = \frac{-55}{-64}$
Vinkel A er 30,75 grader.
Arealsetning:
$A = \frac 12 bc SinA = \frac 12 \cdot 4 \cdot 8 \cdot sin 30,75 = 8,2$
Oppgave 7
a)
$AB = 3,0 \cdot cos 52^{\circ} = 1,85$
Båten ligger 1,85 meter fra brygga.
b)
Ny vannstand:
$AC = 3,0 \cdot sin 52^{\circ} + 0,30 m = 2,66 m $
Bruker Pytagoras og finner ny avstand mellom båt og brygge:
$AB = \sqrt{3^2 - 2,66^2} = 1,40 $
Båten ligger nå 1,40 meter fra brygga.
Oppgave 8
a)
Omkretsen er summen av de tre sidene.
AB = 8
$BC = \sqrt{x^2 + 36}$ (pytagoras)
$AC = \sqrt{(8-x)^2 +36} = \sqrt{64-16x +x^2 + 36} = \sqrt{x^2-16x+100}$
Dersom man legger sammen disse tre uttrykkene får man omkretsfunksjonen f, slik den er gitt i oppgaven:
$f(x) = AB + BC + AC = 8 +\sqrt{x^2 + 36} +\sqrt{x^2-16x+100}$
x må ligge mellom 0 og 8 fordi AB = 8.
b)
Den minste omkretsen får man når x=4 (Geogebra, ekstremalpunkt). Man observerer at det er midtpunktet på AB. AC og BC vil være like lange, trekanten er da likebeint. Når x = 4 er omkretsen 22,42.
Oppgave 9
Han "flipper" først trekantene ADC og DBC på linjestykket AB. Så speilvender han trekanten DBE om linjestykket AB. Punktene F og G har samme avstand (6) fra linjestykket AB. I planet er den korteste vei mellom to punkter en rett linje. Han trekker denne. Den skjærer linjestykket AB i D´. I D´ har vi toppvinkler. I tillegg er vinkel A og B begge 90 grader. Vinklene i trekantene AD´F og GBD´er derfor like. Det er også sidene AF og GB. Av det kan man slutte at disse to trekantene er kongruente, og Petter har rett.