2P 2011 vår LØSNING: Forskjell mellom sideversjoner
m Teksterstatting – «/ressurser/eksamen/» til «/res/eksamen/» |
|||
| (62 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
==MAT 1015== | ==MAT 1015== | ||
[http://ndla.no/nb/node/88902?fag=53 Løsning fra NDLA] | [http://ndla.no/nb/node/88902?fag=53 Løsning fra NDLA] | ||
{{EksLenker|1= | |||
*[http://www.matematikk.net/res/eksamen/2P/sensur/2011V_Sensorveiledning_MAT1015_2P_V2011.pdf Sensorveiledning] | |||
*[http://www.matematikk.net/res/eksamen/2P/sensur/2011V_Forhandsensurrapport_MAT1015_Matematikk_2P_V20.pdf Forhandsensurrapport] | |||
}} | |||
= Del 1 = | = Del 1 = | ||
| Linje 119: | Linje 123: | ||
=== f) === | === f) === | ||
Grunnlaget er forskjellig. | |||
I begge butikkene er prisen 100%. I den ene øker prisen med 20%, da blir den nye prisen 120%. I den andre butikken øker prisen med 10%, da blir den nye prisen 110%. Så øker den med 10% igjen, denne gangen av 110% som gir en total på 11% av det som var før første økning, dvs. en økning på 121% | |||
En vare som koster 100 kroner og blir satt opp 20% koster da 120 kroner. | |||
En vare som koster 100 kroner og blir satt opp 10% koster da 110 kroner. Når den blir satt opp nye 10% er det med grunnlag 110 kroner. 10% av 110 kr. er 11 kroner. Ny pris blir da 121 kroner. | |||
=== g) === | |||
<p></p><table width="50%"> | |||
<tr> | |||
<td>Antall minutter</td> <td>Midtpunkt, $x_m$</td><td>Antall elever, f</td><td>$x_m \cdot f$</td> | |||
</tr> | |||
<tr> | |||
<td>[0,30></td> <td> 15 </td> <td> 1 </td> <td> 15 </td> | |||
</tr> | |||
<tr> | |||
<td>[30,60></td> <td> 45</td> <td> 3 </td> <td> 135 </td> | |||
</tr> | |||
<tr> | |||
<td>[60,120></td> <td> 90</td> <td> 5 </td> <td> 450 </td> | |||
</tr> | |||
<tr> | |||
<td>[120, 240></td> <td>180 </td> <td> 1 </td> <td> 180 </td> | |||
</tr> | |||
<tr> | |||
<td>SUM</td> <td></td> <td> 10 </td> <td> 780 </td> | |||
</tr> | |||
</table> | |||
Vi forutsetter at elevene i de forskjellige intervallene fordeler seg jevnt rundt midtpunktet i intervallet. Dette er derfor en for tilnærming. | |||
Gjennomsnitt $\frac{780}{10} = 78$ minutter. | |||
=== h) === | |||
I tillegg til titallsystemet som vi er relativt godt kjent med har vi blant annet totall- og firetallsystemet. | |||
Totallsystem: 64 - 32 - 16 - 8 - 4 - 2 - 1 | |||
Firetallsystem: 16 - 4 - 1 | |||
$27_{10} = 16 + 8 + 2 + 1 = 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 11011_2 $ | |||
I følge tabellen i oppgaven skal det tilsvare 123 i firetallsystemet. Det betyr at vi trenger en av sekstengruppen to firere og tre enere: | |||
$ 27_{10} = 1 \cdot 16_{10} + 2 \cdot 4_{10} + 3 \cdot 1_{10} = 123_{4} $ | |||
Første rad blir da: | |||
$27_{10} =11011_2 =123_{4}$ | |||
$ 101010_2 = 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 +0 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 32 + 0 +8 + 0+ 2 + 0 = 42_{10}$ | |||
Fra firetallsystemet over ser man at det trengs to sekstengrupper, to firergrupper og to energrupper, det blir 32 + 8 + 2, i firetallsysemet: $ 222_4$ | |||
Tabellen blir da: | |||
$27_{10} =11011_2 =123_{4}$ | |||
$42_{10} = 101010_2= 222_4$ | |||
== Oppgave 2 == | == Oppgave 2 == | ||
=== a) === | |||
= | <p></p><table width="50%"> | ||
<tr> | |||
<td>$^\circ$F</td> <td> 0 </td> <td> 50 </td> <td> 100 </td> | |||
</tr> | |||
<tr> | |||
<td>$^\circ$C</td> <td> -18</td> <td> 10 </td> <td> 38 </td> | |||
</tr> | |||
</table> | |||
=== b og c) === | |||
[[File:2-2p-v2011.png]] | |||
Kaka skal stekes på $178^\circ C$ | |||
= Del 2 = | = Del 2 = | ||
| Linje 143: | Linje 220: | ||
'''1)''' | '''1)''' | ||
En reduksjon på 11% per time gir etter en time: | |||
$220mg \cdot 0,89 = 196mg $ | |||
'''2)''' | '''2)''' | ||
Etter åtte timer: | |||
$220mg \cdot 0,89^8 = 87mg $ | |||
=== b) === | === b) === | ||
| Linje 153: | Linje 234: | ||
'''1)''' | '''1)''' | ||
Her går vi ut fra at antibiotikaen blir tatt opp i kroppen med en gang. I virkeligheten tar det lengre tid. | |||
Hun har 87mg fra første tablett pluss 220mg fra den nye tabletten, dvs. ca 307 mg. antibiotika. | |||
'''2)''' | '''2)''' | ||
Når hun tar den tredje tabletten har hun en liten rest fra den første tabletten i kroppen, en litt større rest fra den andre og 220mg fra den tredje: | |||
$220 \cdot 0,89^{16} + 220 \cdot 0,89^8 + 220 = 220(0,89^{16} + 0,89^8 + 0,89^0) = 220 + 87 + 34 = 341$mg | |||
=== c) === | === c) === | ||
[[File:3c-2p-v2011.png]] | |||
== Oppgave 4 == | == Oppgave 4 == | ||
=== a) === | === a) === | ||
[[file:4a-2p-v2011.png]] [[File:4a2-2p-v2011.png]] | |||
=== b) === | |||
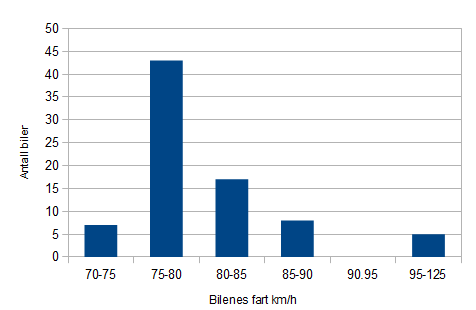
50 sone: ti prosent for fort, eller mer vil si alle biler som kjører i 55 km/h eller fortere. | |||
Det er totalt 29 biler som kjører for fort, av 80. : $\frac{29}{80} \cdot 100 \percent = 36,3 \percent $ | |||
80 sone: ti prosent for fort, eller mer vil si alle biler som kjører 88km/h eller fortere. Åtte biler kjører mellom 85 og 90 km/h. Dersom man antar at bilene fordeler seg jevnt i intervallet, (noe vi ikke har holdepunkter for ut fra dataene), vil ca. tre biler ligge over 88 km/h. Det vil da til sammen være 8 biler som kjørere mer enn 10% for fort, av 80 biler. Det er 10% av de bilene som ble målt. | |||
=== c) === | |||
FEMTISONE: | |||
[[File:4c-2p-v2011.png]] | |||
ÅTTISONE: | |||
[[File:4c2-2p-v2011.png]] | |||
=== | === d) === | ||
Her testes prosentvis del av det hele nok en gang, litt fantasiløst og unødvendig, men her er løsningen: | |||
= | $\frac {3}{80} \cdot 100 \percent = 3,8 \percent$ | ||
I femtisonen ligger gjennomsnittsfarten ca 4 % over fartsgrensen. | |||
= | $ \frac {1}{80} \cdot 100 \percent = 1,3 \percent $ | ||
I åttisonen ligger gjennomsnittsfarten drøye en prosent over fartsgrensen. | |||
=== e) === | === e) === | ||
I femtisonen er det flere som kjører for fort. De fleste av disse kjører bare "litt" for fort. I åttisonen er det ikke så mange som kjørere for fort, men fem av disse kjører mye for fort. | |||
== Oppgave 5 == | == Oppgave 5 == | ||
=== a) === | === a) === | ||
$(40-32) \cdot 0,66 + 21,75 = 27 cm$ | |||
=== b) === | === b) === | ||
| Linje 189: | Linje 300: | ||
'''1)''' | '''1)''' | ||
20 er minste størrelse. (x-20) blir antall størrelser over minste størrelse. En størrelse opp øker skoens lengde med 0,5 cm. $(x-20) \cdot 0,5$ blir da lengden over minstelengden. Når man plusser på 21,5 finner man lengden y til skostørrelse x. | |||
'''2)''' | |||
$y_{norsk} = (x-32) \cdot 0,66 + 21,75$ Centimeter | |||
=== c) === | |||
Størrelse 43 i norske sko gir skolengde: | |||
$(x-32) \cdot 0,66 +21,75 = 29$cm | |||
I kinesisk skostørrelse tilsvarer det | |||
$29 = (x-20) \cdot 0.5 + 21,5 \\ x = 35$ | |||
Norsk størrelse 43 tilsvarer kinesisk størrelse 35. | |||
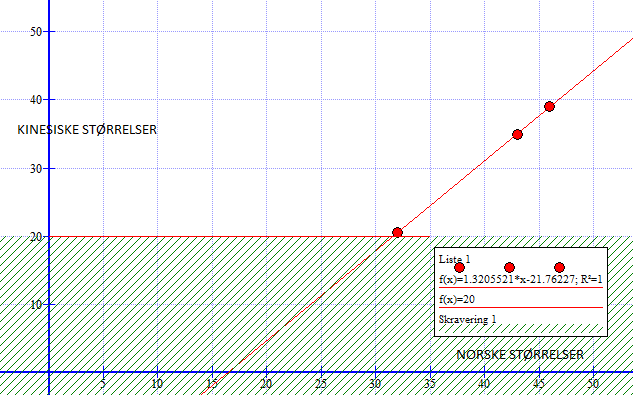
=== d) === | |||
= | <p></p><table width="50%"> | ||
<tr> | |||
<td>Norsk størrelse</td> <td> Kinesisk størrelse </td> | |||
</tr> | |||
<tr> | |||
<td>32</td> <td> 20,5</td> | |||
</tr> | |||
<tr> | |||
<td>43</td> <td> 35</td> | |||
</tr> | |||
<tr> | |||
<td>46</td> <td> 39</td> | |||
</tr> | |||
</table> | |||
[[File:5d-2p-v2011.png]] | |||
= | Formelen $y = 1,32x-21,8$ gjelder når x er et heltall større eller lik 32. | ||
== Oppgave 6 == | |||
=== a) === | |||
$29 = 16 + 8 + 4 + 0 + 1 = 2^4 + 2^3 +2^2 + 2^0$ | |||
=== | === b) === | ||
$1 + 0+ 4 + 8 + 16 \\ 25 + 0 + 100 + 200 + 400 = 725 $ | |||
=== c) === | |||
Den kan brukes fordi "hoppet" fra en toerpotens til den neste er en dobling. | |||
== Oppgave 7 == | == Oppgave 7 == | ||
| Linje 220: | Linje 361: | ||
'''1)''' | '''1)''' | ||
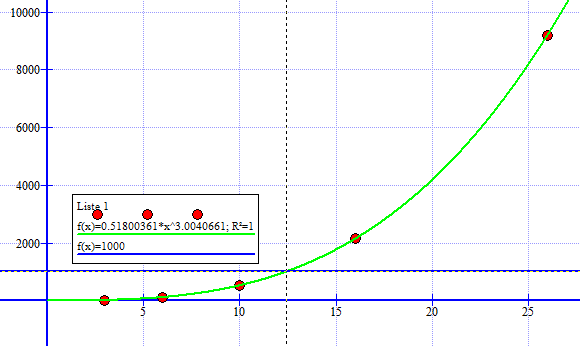
Fra figuren nedenfor ser man at $f(x) = 0,52 \cdot x^{3,0}$ er en god modell for sammenhengen mellom diameter og volum til kulene. | |||
'''2)''' | '''2)''' | ||
[[File: 7ab-2p-v2011.png]] | |||
=== b) === | ===b)=== | ||
Fra figuren over ser man at diameteren er 12,4 cm. når volumet er 1000ml. | |||
=== c) === | === c) === | ||
$V = \frac 43 \pi r^3 \\ Diameter \quad = x \\ r = \frac x2 \\ V = \frac 43 \pi ( \frac x2)^3 \\ V = \frac{4 \cdot \pi}{3 \cdot 8}x^3 \\ V = 0,52x^3 $ | |||
Dette er i samsvar med modellen i a. | |||
Siste sideversjon per 19. okt. 2014 kl. 17:07
MAT 1015
Del 1
Oppgave 1
a)
1) <math> 36 200 = 3.62 \cdot 10^4 </math>
2) <math> 0.000 642 = 6.42 \cdot 10^{-4} </math>
3) <math> 53 \text{ millioner} = 5.3 \cdot 10^7 </math>
4) <math> 0.034 \cdot 10^{-2} = 3.4 \cdot 10^{-4} </math>
b)
| Prosentvis endring | Vekstfaktor |
| + 2% | 1 + 0,02 = 1,02 |
| - 68 % | 1-0,68 = 0,32 |
| -75% | 0,25 |
| + 100% | 2 |
c)
1) <math>a^4 \cdot \big( a^2 \big)^{-3} \cdot a^0 = a^4 \cdot a^{2 \cdot (-3)} \cdot a^0 = a^4 \cdot a^{-6} \cdot a^0 = a^{4 - 6 + 0} = a^{-2}</math>
2) <math>\frac{2^{-3} \cdot 4^3 } {8^2} = \frac{2^{-3} \cdot (2^2)^3 } {(2^3)^2} = \frac{2^{-3} \cdot 2^6 } {2^6} = 2^{-3} = \frac{1}{8} </math>
d)
0, 0, 2, 2, 2, 3, 4, 5, 5, 5
1)
Median = <Math>\frac {2+3}{2} = 2,5</Math>
Gjennomsnitt = <Math>\frac {2+2+2+3+4+5+5+5}{10} = 2,8</Math>
2)
| Antall Mål | Frekvens | Kumulativ Frekvens |
| 0 | 2 | 2 |
| 1 | 0 | 2 |
| 2 | 3 | 5 |
| 3 | 1 | 6 |
| 4 | 1 | 7 |
| 5 | 3 | 10 |
3) Den kumulative frekvensen for to mål er fem. Det betyr at i fem av kampene ble det skåret to mål eller mindre.
e)
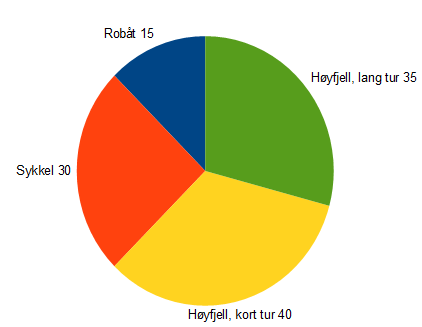
| TUR | Antall elever | Gradetall, sektor |
| Robåt | 15 | $ \frac{15 \cdot 360^{\circ}}{120} = 45^{\circ}$ |
| Sykkel | 30 | $ \frac{30 \cdot 360^{\circ}}{120} = 90^{\circ}$ |
| Høyfjell, kort løype | 40 | $ \frac{40 \cdot 360^{\circ}}{120} = 120^{\circ}$ |
| Høyfjell, lang løype | 35 | $ \frac{35 \cdot 360^{\circ}}{120} = 105^{\circ}$ |
f)
Grunnlaget er forskjellig. I begge butikkene er prisen 100%. I den ene øker prisen med 20%, da blir den nye prisen 120%. I den andre butikken øker prisen med 10%, da blir den nye prisen 110%. Så øker den med 10% igjen, denne gangen av 110% som gir en total på 11% av det som var før første økning, dvs. en økning på 121%
En vare som koster 100 kroner og blir satt opp 20% koster da 120 kroner.
En vare som koster 100 kroner og blir satt opp 10% koster da 110 kroner. Når den blir satt opp nye 10% er det med grunnlag 110 kroner. 10% av 110 kr. er 11 kroner. Ny pris blir da 121 kroner.
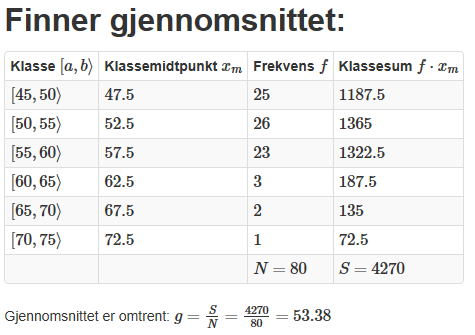
g)
| Antall minutter | Midtpunkt, $x_m$ | Antall elever, f | $x_m \cdot f$ |
| [0,30> | 15 | 1 | 15 |
| [30,60> | 45 | 3 | 135 |
| [60,120> | 90 | 5 | 450 |
| [120, 240> | 180 | 1 | 180 |
| SUM | 10 | 780 |
Vi forutsetter at elevene i de forskjellige intervallene fordeler seg jevnt rundt midtpunktet i intervallet. Dette er derfor en for tilnærming.
Gjennomsnitt $\frac{780}{10} = 78$ minutter.
h)
I tillegg til titallsystemet som vi er relativt godt kjent med har vi blant annet totall- og firetallsystemet.
Totallsystem: 64 - 32 - 16 - 8 - 4 - 2 - 1
Firetallsystem: 16 - 4 - 1
$27_{10} = 16 + 8 + 2 + 1 = 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 11011_2 $
I følge tabellen i oppgaven skal det tilsvare 123 i firetallsystemet. Det betyr at vi trenger en av sekstengruppen to firere og tre enere:
$ 27_{10} = 1 \cdot 16_{10} + 2 \cdot 4_{10} + 3 \cdot 1_{10} = 123_{4} $
Første rad blir da:
$27_{10} =11011_2 =123_{4}$
$ 101010_2 = 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 +0 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 32 + 0 +8 + 0+ 2 + 0 = 42_{10}$
Fra firetallsystemet over ser man at det trengs to sekstengrupper, to firergrupper og to energrupper, det blir 32 + 8 + 2, i firetallsysemet: $ 222_4$
Tabellen blir da:
$27_{10} =11011_2 =123_{4}$
$42_{10} = 101010_2= 222_4$
Oppgave 2
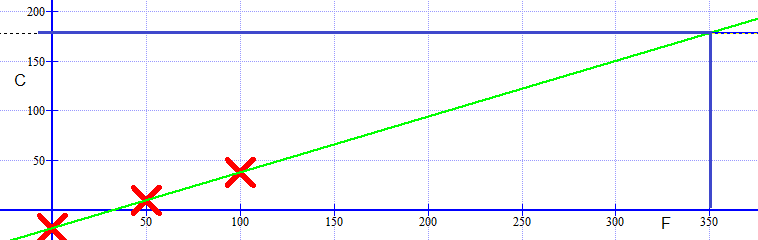
a)
| $^\circ$F | 0 | 50 | 100 |
| $^\circ$C | -18 | 10 | 38 |
b og c)
Kaka skal stekes på $178^\circ C$
Del 2
Oppgave 3
a)
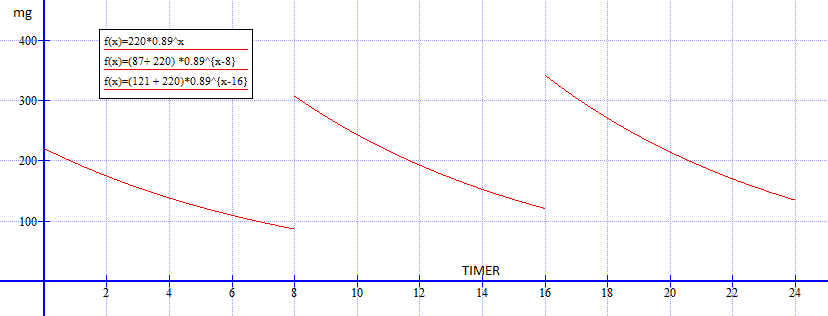
1) En reduksjon på 11% per time gir etter en time:
$220mg \cdot 0,89 = 196mg $
2) Etter åtte timer:
$220mg \cdot 0,89^8 = 87mg $
b)
1) Her går vi ut fra at antibiotikaen blir tatt opp i kroppen med en gang. I virkeligheten tar det lengre tid.
Hun har 87mg fra første tablett pluss 220mg fra den nye tabletten, dvs. ca 307 mg. antibiotika.
2)
Når hun tar den tredje tabletten har hun en liten rest fra den første tabletten i kroppen, en litt større rest fra den andre og 220mg fra den tredje:
$220 \cdot 0,89^{16} + 220 \cdot 0,89^8 + 220 = 220(0,89^{16} + 0,89^8 + 0,89^0) = 220 + 87 + 34 = 341$mg
c)
Oppgave 4
a)
b)
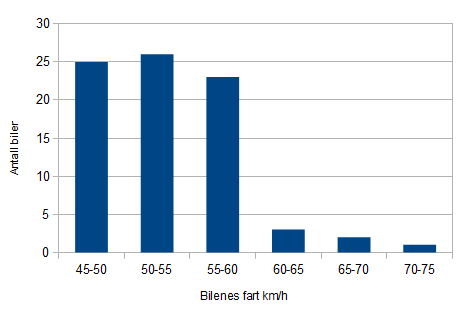
50 sone: ti prosent for fort, eller mer vil si alle biler som kjører i 55 km/h eller fortere.
Det er totalt 29 biler som kjører for fort, av 80. : $\frac{29}{80} \cdot 100 \percent = 36,3 \percent $
80 sone: ti prosent for fort, eller mer vil si alle biler som kjører 88km/h eller fortere. Åtte biler kjører mellom 85 og 90 km/h. Dersom man antar at bilene fordeler seg jevnt i intervallet, (noe vi ikke har holdepunkter for ut fra dataene), vil ca. tre biler ligge over 88 km/h. Det vil da til sammen være 8 biler som kjørere mer enn 10% for fort, av 80 biler. Det er 10% av de bilene som ble målt.
c)
FEMTISONE:
ÅTTISONE:
d)
Her testes prosentvis del av det hele nok en gang, litt fantasiløst og unødvendig, men her er løsningen:
$\frac {3}{80} \cdot 100 \percent = 3,8 \percent$
I femtisonen ligger gjennomsnittsfarten ca 4 % over fartsgrensen.
$ \frac {1}{80} \cdot 100 \percent = 1,3 \percent $
I åttisonen ligger gjennomsnittsfarten drøye en prosent over fartsgrensen.
e)
I femtisonen er det flere som kjører for fort. De fleste av disse kjører bare "litt" for fort. I åttisonen er det ikke så mange som kjørere for fort, men fem av disse kjører mye for fort.
Oppgave 5
a)
$(40-32) \cdot 0,66 + 21,75 = 27 cm$
b)
1) 20 er minste størrelse. (x-20) blir antall størrelser over minste størrelse. En størrelse opp øker skoens lengde med 0,5 cm. $(x-20) \cdot 0,5$ blir da lengden over minstelengden. Når man plusser på 21,5 finner man lengden y til skostørrelse x.
2)
$y_{norsk} = (x-32) \cdot 0,66 + 21,75$ Centimeter
c)
Størrelse 43 i norske sko gir skolengde:
$(x-32) \cdot 0,66 +21,75 = 29$cm
I kinesisk skostørrelse tilsvarer det
$29 = (x-20) \cdot 0.5 + 21,5 \\ x = 35$
Norsk størrelse 43 tilsvarer kinesisk størrelse 35.
d)
| Norsk størrelse | Kinesisk størrelse |
| 32 | 20,5 |
| 43 | 35 |
| 46 | 39 |
Formelen $y = 1,32x-21,8$ gjelder når x er et heltall større eller lik 32.
Oppgave 6
a)
$29 = 16 + 8 + 4 + 0 + 1 = 2^4 + 2^3 +2^2 + 2^0$
b)
$1 + 0+ 4 + 8 + 16 \\ 25 + 0 + 100 + 200 + 400 = 725 $
c)
Den kan brukes fordi "hoppet" fra en toerpotens til den neste er en dobling.
Oppgave 7
a)
1)
Fra figuren nedenfor ser man at $f(x) = 0,52 \cdot x^{3,0}$ er en god modell for sammenhengen mellom diameter og volum til kulene.
2)
b)
Fra figuren over ser man at diameteren er 12,4 cm. når volumet er 1000ml.
c)
$V = \frac 43 \pi r^3 \\ Diameter \quad = x \\ r = \frac x2 \\ V = \frac 43 \pi ( \frac x2)^3 \\ V = \frac{4 \cdot \pi}{3 \cdot 8}x^3 \\ V = 0,52x^3 $
Dette er i samsvar med modellen i a.