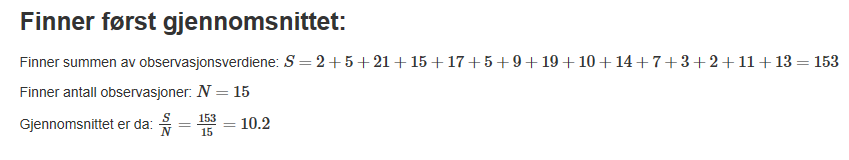2P 2011 høst LØSNING: Forskjell mellom sideversjoner
m Teksterstatting – «/ressurser/eksamen/» til «/res/eksamen/» |
|||
| (49 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
==MAT 1015== | ==MAT 1015== | ||
[http://ndla.no/nb/node/92723?fag=53 Løsning fra NDLA] | {{EksLenker|1= | ||
*[http://ndla.no/nb/node/92723?fag=53 Løsning fra NDLA] | |||
*[http://www.matematikk.net/res/eksamen/2P/sensur/2011H_Vurderingsskjema_MAT1015_Matematikk_2P_H11.pdf Vurderingsskjema] | |||
*[http://www.matematikk.net/res/eksamen/2P/sensur/2011H_Sensorveiledning_MAT1015_Matematikk_2P_H11 Sensorveiledning] | |||
}} | |||
==DEL EN== | ==DEL EN== | ||
| Linje 93: | Linje 97: | ||
|+ | |+ | ||
|- | |- | ||
! | ! | ||
! | ! April | ||
! | !Mai | ||
! | ! Juni | ||
|- | |- | ||
! | ! Per | ||
| | | 225 || 90 || 450 | ||
|- | |- | ||
! | ! Pål | ||
| | |675 || 180 || 450 | ||
|- | |- | ||
! | ! Espen | ||
| | | 0 || 630 || 900 | ||
|- | |- | ||
|} | |||
a) | |||
[[File:2a1-2p-h2011.png]] | |||
[[File:2a2-2p-h2011.png]] | |||
b) | |||
[[File:2b-2p-h2011.png]] | |||
==DEL TO== | |||
==Oppgave 3== | |||
a) | |||
Boken skulle vært levert for hundre år siden, altså er man 5200 uker for sent ute. | |||
Modeller: | |||
Gebyr1 (x) = $ 0,10 + (x-1)\cdot 0,05 $ | |||
Gebyr2 (x) = $ 0,10 \cdot 1,002^{x-1} $ | |||
Dersom modell 1 betales det: Gebyr1 (5200) = $ 0,10 + (5200-1)\cdot 0,05 = 260kr $ | |||
Dersom modell 2 betales det: Gebyr2 (5200) = $ 0,10 \cdot 1,002^{5200-1} = 3246 kr $ | |||
b) | |||
[[File:3b-2p-h2011.png]] | |||
Man observerer at den lineære modellen, modell en først kommer opp i ti kroner, etter ca. 198 uker. Den eksponentielle modellen når ti kroner etter ca. 2305 uker. Modellene gir like store kostnader etter ca. 3776 uker. | |||
==Oppgave 4== | |||
a) | |||
1) | |||
{| class="wikitable" style="text-align:center; width:200px; height:200px;" | |||
|+ | |||
|- | |||
!Årstall | |||
! 2005 | |||
!2006 | |||
! 2007 | |||
! 2008 | |||
!2009 | |||
! 2010 | |||
|- | |||
! Innbyggertall | |||
| 650 || 550 || 467 || 396 || 336|| 284 | |||
|- | |- | ||
! | ! Endring fra året før | ||
| || | | || -100|| -83|| -71|| -60|| -52 | ||
|- | |||
! Prosentvis endring fra året før | |||
| || -15,4% || -15,1% || -15,2% || -15,2%||-15,5% | |||
|- | |- | ||
| Linje 116: | Linje 182: | ||
|} | |} | ||
= | 2) | ||
Dersom antallet personer hadde avtatt med samme antall hvert år ville en lineær modell være fornuftig. Her ser man at den prosentvise nedgangen er tilnærmet konstant fra år til år, derfor er en eksponentiell modell det beste her, ut fra foreliggende datamengder (man har jo ingen garanti for at denne utviklingen vil fortsette). | |||
b) | |||
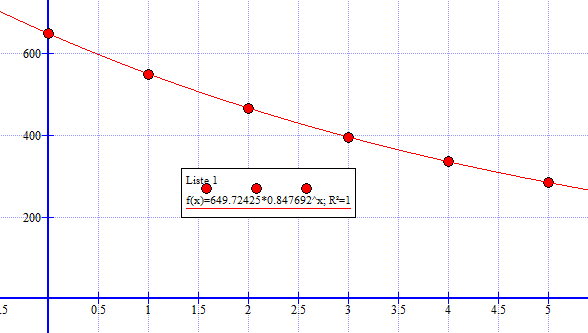
[[File: 4b-2p-h2011.png]] | |||
Man observerer at tilpasningen er god og at modellen er $ f(x) = 649,7 \cdot 0,848^x$ | |||
c) | |||
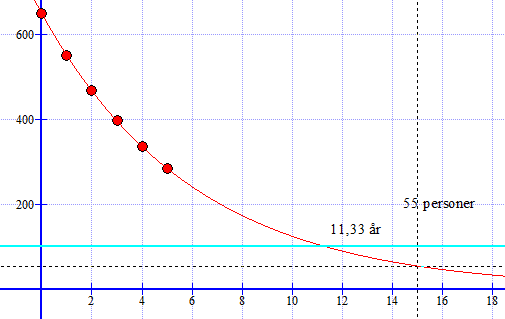
[[File: 4c-2p-h20111.png]] | |||
1) ca. 55 personer, fra figur. | |||
2) ca,11,33 år, fra figur. Dvs. i første halvdel av 2016. | |||
d) | |||
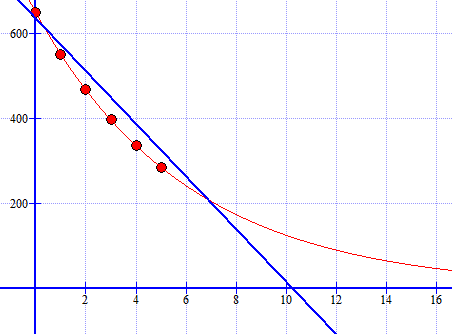
[[File:4d-2p-h2011.png]] | |||
Modellen (blå graf) er ikke brukbar i det hele tatt. Fra ca. 2015 gir den et negativt innbyggertall. Før 2012 overestimerer den antall innbyggere. | |||
==Oppgave 5== | ==Oppgave 5== | ||
a) | |||
[[File:5a1-2p-h2011.png]] = $ 2 \cdot 20^2 + 3 \cdot 20^1 + 17\cdot 20^0 = 800 + 60 + 17 = 877$ | |||
b) | |||
$ 76 = 60 +16 = 3 \cdot 20^1 + 16 \cdot 20^0 = $ [[File:5b-2p-h2011.png]] | |||
==Oppgave 6== | ==Oppgave 6== | ||
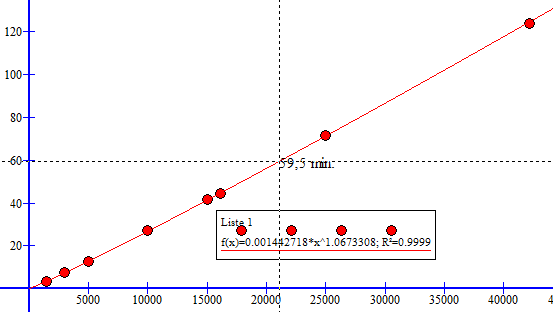
[[File: 5a-2p-h2011.png]] | |||
a) | |||
Fra figuren over: $ 0,001443 \cdot x^{1,067} = 1,44 \cdot 10{-3} \cdot x^{1,07}$ | |||
b) | |||
Se figuren over. | |||
c) | |||
Det tar ca 59,5 minutter, i følge figuren over. | |||
d) | |||
$ \frac{T_2}{T_1}= \frac{D_2}{D_1}^{1,06} \\ \frac{T_2}{71,617 min}= (\frac{20097,5m}{25000m})^{1,06} \\ T_2 = 71,617 min \cdot 0,8353499 \\ T_2 = 59,8min$ | |||
Dette stemmer godt med modellen i a, avviket er mindre enn 20 sekunder. | |||
==Oppgave 7== | ==Oppgave 7== | ||
a) | |||
Bruker sannsynlighetskalkulatoren på matematikk.net og får: | |||
Gjennomsnitt | |||
[[File:7a1-2p-h2011.png]] | |||
Standard avvik | |||
[[File:7a2-2p-h2011.png]] | |||
Median | |||
[[File:7a3-2p-h2011.png]] | |||
b) | |||
Ved en dobling av alle verdiene finner man: | |||
Gjennomsnitt | |||
[[File:7b1-2p-h2011.png]] | |||
Standard avvik | |||
[[File:7b2-2p-h2011.png]] | |||
Median | |||
[[File:7b3-2p-h2011.png]] | |||
c) | |||
Dersom antall tall i mengden er konstant og hver enkelt tallverdi dobles, vil median, gjennomsnitt og standardavvik også dobles. Dersom du synes dette er vanskelig å forstå kan du leke med små tallmengder. Prøv | |||
1,2,3 | |||
2,4,6 | |||
100, 200, 300. | |||
Siste sideversjon per 19. okt. 2014 kl. 17:07
MAT 1015
DEL EN
Oppgave 1
a)
1) 533 milliarder = 533 000 000 000 = <Math>5,33 \cdot 10^{11}</Math>
2) <math>0,000533 = 5,33 \cdot 10^{-4}</math>
b)
1) <math> 8 \cdot 2^{-2} = 8 \cdot \frac{1}{2^2} = \frac{8 \cdot 1}{4} = 2 </math>
2) <math> 2^3 \cdot (\frac{3}{2})^2 = 8 \cdot \frac{ 9} {4 } = \frac {8 \cdot 9 }{4 } = 2 \cdot 9 = 18</math>
c)
2, 1, 3, 4, 5, 5, 3, 6, 4, 3
Vi ordner i stigende rekkefølge:
1, 2, 3, 3, 3, 4, 4, 5, 5, 6
Median er de to tallene i midten, delt på to. 3 + 4 = 7. Så deler man på to: 7:2 = 3,5
Variasjonsbredden er 6 - 1 = 5, forteller oss bare at hele skalaen er i bruk.
Gjennomsnitt: <Math> \frac{1+2+3+3+3+4+4+5+5+6}{10} = 3,6</Math>
d)
40 000km = 40 000 000m
20cm/ ball = 0,2m/ ball
<math>\frac{4\cdot 10^7}{2 \cdot 10^{-1} } fotballer = 2 \cdot 10^8</math> fotballer.
e)
1)
<math>11_{2} = 2^1 + 2^0 = 3_{10} \\ 110_2 = 2^2+2^1 = 6_{10} \\ 1100_2 = 2^3 + 2^2 = 12_{10}</math>
2)
Alle verdigivene siffer øker med faktoren to, se oppgaven over, derfor blir tallet dobblet når man legger til en null bakerst.
3)
Følger vi systemet over er 24 = 11000 og 48 = 110000.
f)
De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56.
g)
| Fart (km/t) | Antall biler | klassemidtpunkt | klassemidtpunkt <Math> \cdot </Math> frekvens |
|---|---|---|---|
| [20,30> | 20 | 25 | 500 |
| [30,40> | 20 | 35 | 700 |
| [40,50> | 10 | 45 | 450 |
| 1650 |
Gjennomsnitt: 1650:50 = 33 kilometer i timen.
h)
Han har hatt en måned med 5 prosent vekst, to måneder med 0,8 prosent vekst og tre måneder med 15 prosent nedgang.
Oppgave 2
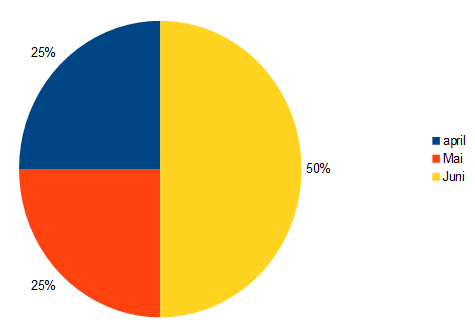
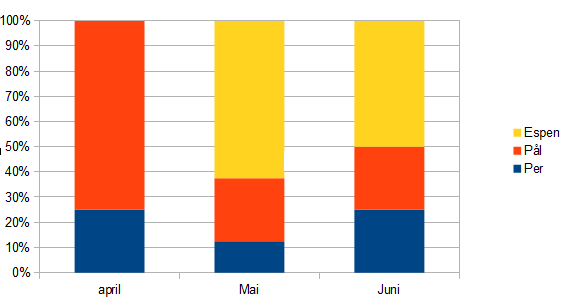
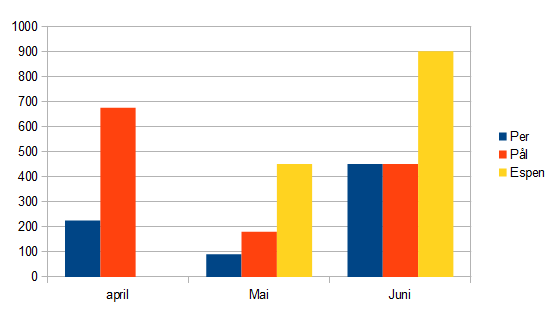
| April | Mai | Juni | |
|---|---|---|---|
| Per | 225 | 90 | 450 |
| Pål | 675 | 180 | 450 |
| Espen | 0 | 630 | 900 |
a)
b)
DEL TO
Oppgave 3
a)
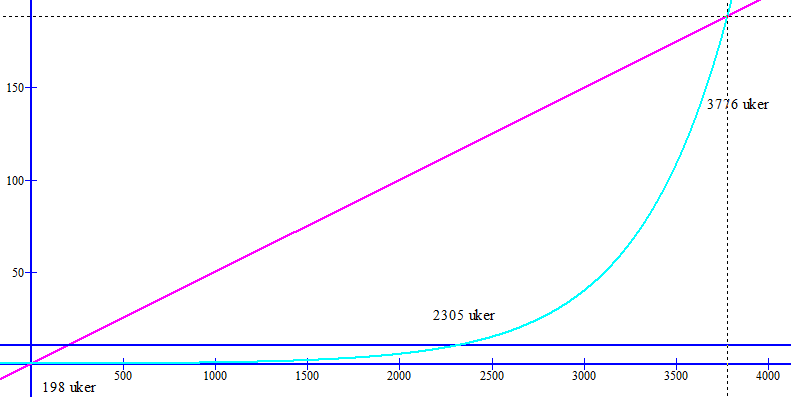
Boken skulle vært levert for hundre år siden, altså er man 5200 uker for sent ute.
Modeller:
Gebyr1 (x) = $ 0,10 + (x-1)\cdot 0,05 $
Gebyr2 (x) = $ 0,10 \cdot 1,002^{x-1} $
Dersom modell 1 betales det: Gebyr1 (5200) = $ 0,10 + (5200-1)\cdot 0,05 = 260kr $
Dersom modell 2 betales det: Gebyr2 (5200) = $ 0,10 \cdot 1,002^{5200-1} = 3246 kr $
b)
Man observerer at den lineære modellen, modell en først kommer opp i ti kroner, etter ca. 198 uker. Den eksponentielle modellen når ti kroner etter ca. 2305 uker. Modellene gir like store kostnader etter ca. 3776 uker.
Oppgave 4
a)
1)
| Årstall | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|---|
| Innbyggertall | 650 | 550 | 467 | 396 | 336 | 284 |
| Endring fra året før | -100 | -83 | -71 | -60 | -52 | |
| Prosentvis endring fra året før | -15,4% | -15,1% | -15,2% | -15,2% | -15,5% |
2)
Dersom antallet personer hadde avtatt med samme antall hvert år ville en lineær modell være fornuftig. Her ser man at den prosentvise nedgangen er tilnærmet konstant fra år til år, derfor er en eksponentiell modell det beste her, ut fra foreliggende datamengder (man har jo ingen garanti for at denne utviklingen vil fortsette).
b)
Man observerer at tilpasningen er god og at modellen er $ f(x) = 649,7 \cdot 0,848^x$
c)
1) ca. 55 personer, fra figur.
2) ca,11,33 år, fra figur. Dvs. i første halvdel av 2016.
d)
Modellen (blå graf) er ikke brukbar i det hele tatt. Fra ca. 2015 gir den et negativt innbyggertall. Før 2012 overestimerer den antall innbyggere.
Oppgave 5
a)
 = $ 2 \cdot 20^2 + 3 \cdot 20^1 + 17\cdot 20^0 = 800 + 60 + 17 = 877$
= $ 2 \cdot 20^2 + 3 \cdot 20^1 + 17\cdot 20^0 = 800 + 60 + 17 = 877$
b)
$ 76 = 60 +16 = 3 \cdot 20^1 + 16 \cdot 20^0 = $ 
Oppgave 6
a)
Fra figuren over: $ 0,001443 \cdot x^{1,067} = 1,44 \cdot 10{-3} \cdot x^{1,07}$
b)
Se figuren over.
c)
Det tar ca 59,5 minutter, i følge figuren over.
d)
$ \frac{T_2}{T_1}= \frac{D_2}{D_1}^{1,06} \\ \frac{T_2}{71,617 min}= (\frac{20097,5m}{25000m})^{1,06} \\ T_2 = 71,617 min \cdot 0,8353499 \\ T_2 = 59,8min$
Dette stemmer godt med modellen i a, avviket er mindre enn 20 sekunder.
Oppgave 7
a)
Bruker sannsynlighetskalkulatoren på matematikk.net og får:
Gjennomsnitt
Standard avvik
Median
b)
Ved en dobling av alle verdiene finner man:
Gjennomsnitt
Standard avvik
Median
c)
Dersom antall tall i mengden er konstant og hver enkelt tallverdi dobles, vil median, gjennomsnitt og standardavvik også dobles. Dersom du synes dette er vanskelig å forstå kan du leke med små tallmengder. Prøv
1,2,3
2,4,6
100, 200, 300.