2P-Y 2013 vår LØSNING: Forskjell mellom sideversjoner
m Teksterstatting – «/ressurser/eksamen/» til «/res/eksamen/» |
|||
| (2 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
[http://matematikk.net/ | [http://matematikk.net/res/eksamen/2PY/2P-Y_V13.pdf Oppgaven som pdf] | ||
[http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=35190 Diskusjon av denne oppgaven] | [http://www.matematikk.net/matteprat/viewtopic.php?f=13&t=35190 Diskusjon av denne oppgaven] | ||
| Linje 120: | Linje 120: | ||
Konverterer | Konverterer | ||
${{\color{red}{1}\cdot 2^{4}+\color{red}{1}\cdot 2^{3}+\color{red}{0}\cdot 2^{2}+\color{red}{1}\cdot 2^{1}+\color{red}{0}\cdot 2^{0} | ${26_{(10) } } = {16+8+0+2+0}= {{\color{red}{1}\cdot 2^{4}+\color{red}{1}\cdot 2^{3}+\color{red}{0}\cdot 2^{2}+\color{red}{1}\cdot 2^{1}+\color{red}{0}\cdot 2^{0}}} = {\color{red}{ \underline{ \underline{11010_{(2)} } } }}$ | ||
==Oppgave 6== | ==Oppgave 6== | ||
Siste sideversjon per 19. okt. 2014 kl. 17:07
Del 1
Oppgave 1
a)
Finn median:
Sorterer observasjonene:
Finner antall observasjoner:
Finner midtpunktet:
Fordi det er et partall antall observasjoner er medianen lik gjennomsnittet av de to verdiene som ligger på hver sin side av midtpunktet
Medianen er gjennomsnittet av verdiene nummer 5 og 6.
Finner gjennomsnitt:
Finner summen av observasjonsverdiene:
Finner antall observasjoner:
Gjennomsnittet er da:
Finn typetall:
Teller opp verdiene og lager en frekvenstabell:
| Verdi | Frekvens |
|---|---|
Ser i tabellen og finner de hyppigst forekommende verdiene
Typetall(ene) er: 1
b)
| Verdi x | Frekvens f | Kumulativ frekvens |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 2 | 3+2 = 5 |
| 3 | 2 | 5+2 = 7 |
| 4 | 1 | 7+1 = 8 |
| 5 | 2 | 8 + 2 = 10 |
Oppgave 2
Oppgave 3
A:
B:
Fordi
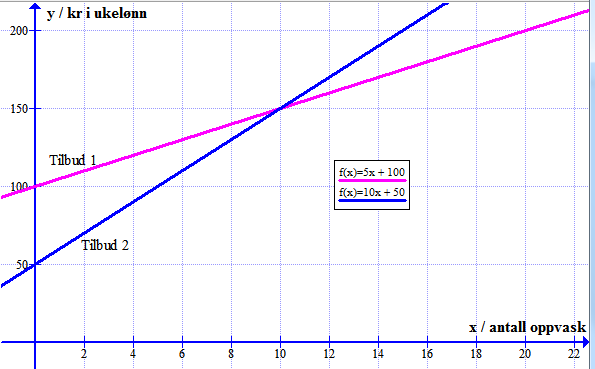
Oppgave 4
a)
Tilbud 1:
Tilbud 2:
b)
Ettersom dette er del 1 av eksamen, må denne grafen skisseres for hånd, men jeg bruker her Graph
Ser av grafen at det lønner seg for Sigvald med tilbud 1 dersom han vasker opp mindre enn 10 ganger i uka. Vi vet ikke hvor ofte de vasker opp i familien, men hvis de for eksempel vasker opp en gang om dagen, så lønner det seg for Sigvald med Tilbud 1.
Oppgave 5
| Plassverdisystem med grunntall 10 | Plassverdisystem med grunntall 2 |
|---|---|
Konverterer
Konverterer
Oppgave 6
a)
b)
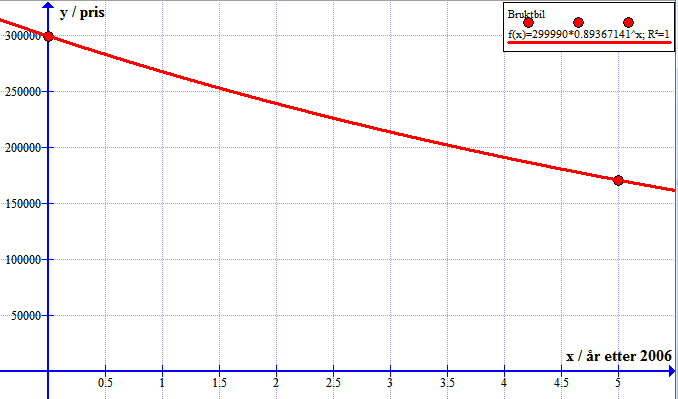
Graf C tilhører f.
Vi ser at graf A er en rett linje, men
Graf C synker raskest i starten, men etterhvert som bilen blir billigere så går den mindre ned i verdi hvert år. Prisen synker med 10% hvert år, og det blir 10% av et mindre og mindre beløp.
Oppgave 7
| Inntekt (i 1000 kroner) | Klassemidtpunkt |
Antall personer |
Klassesum |
Gjennomsnittet er omtrent:
Oppgave 8
Løsning med krysstabell
a)
| Vært i USA | Ikke vært i USA | Totalt | |
|---|---|---|---|
| Vært i Spania | 4 | 7 | 11 |
| Ikke vært i Spania | 4 | 5 | 9 |
| Totalt | 8 | 12 | 20 |
b)
c)
Del 2
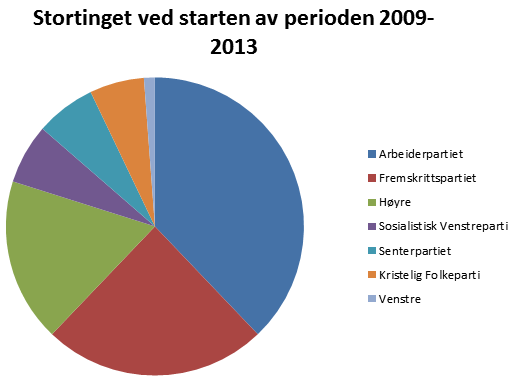
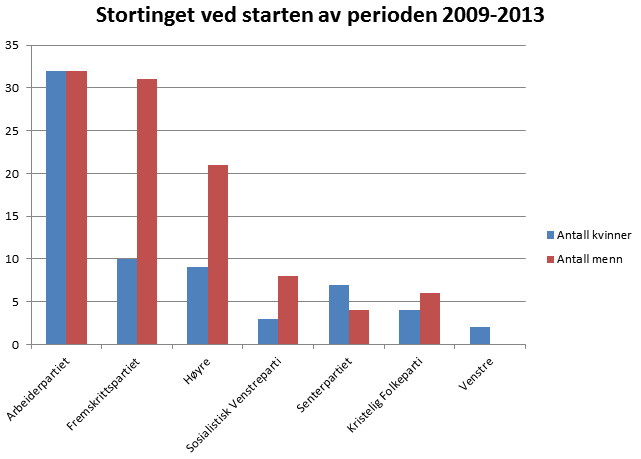
Oppgave 1
a)
Bruker Excel for å tegne sektordiagrammet..
b)
Oppgave 2
a)
Bruker programmet Graph Bruker funksjonen: "Sett inn funksjon".
b)
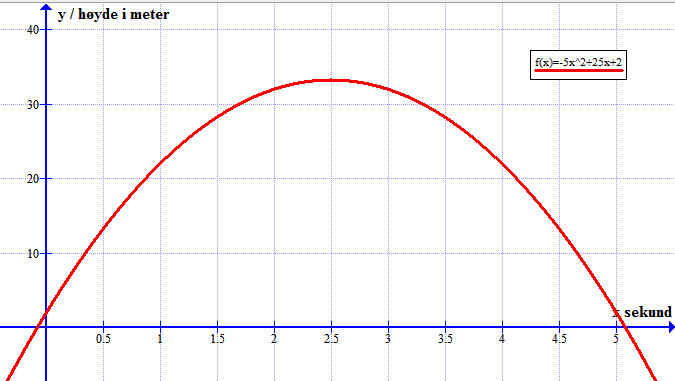
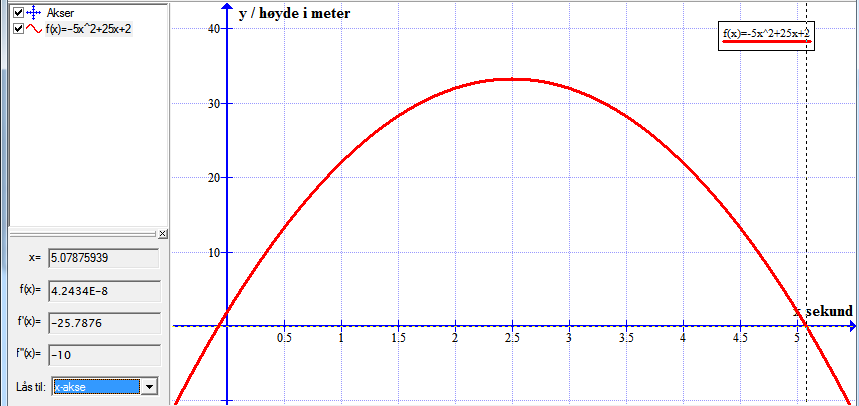
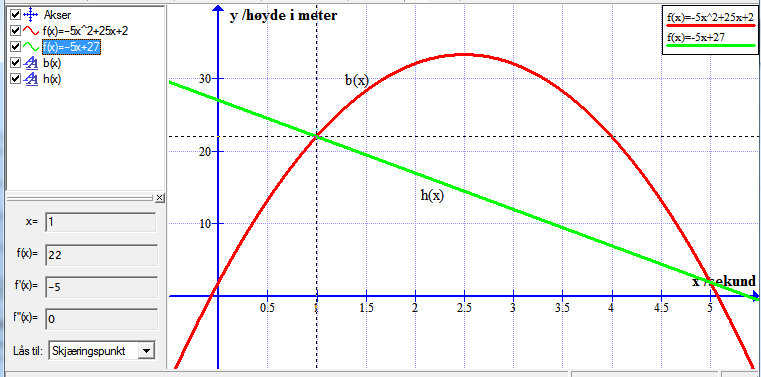
Bruker funksjonen: Beregn => "Lås til x-aksen" for å finne når ballen treffer bakken.
Leser av grafen at den treffer bakken ved tid 5.1 sekunder.
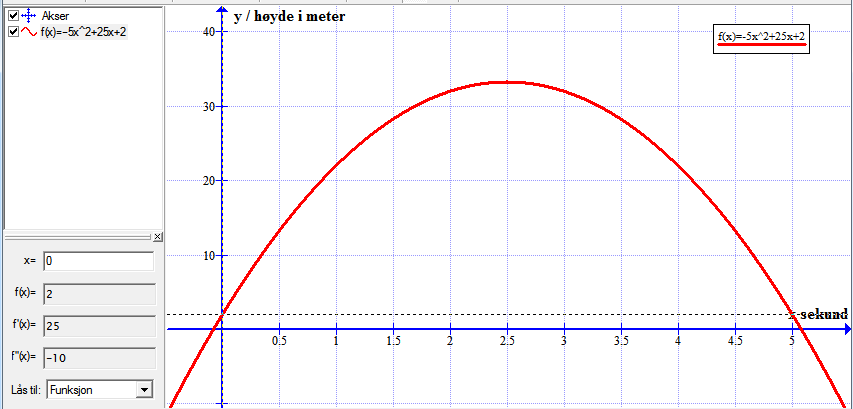
Bruker funksjonen: Beregn => "Lås til funksjon" for å finne høyden når ballen kastes. Velger x=0.
Leser av grafen at den er 2 meter over bakken når den kastes.
c)
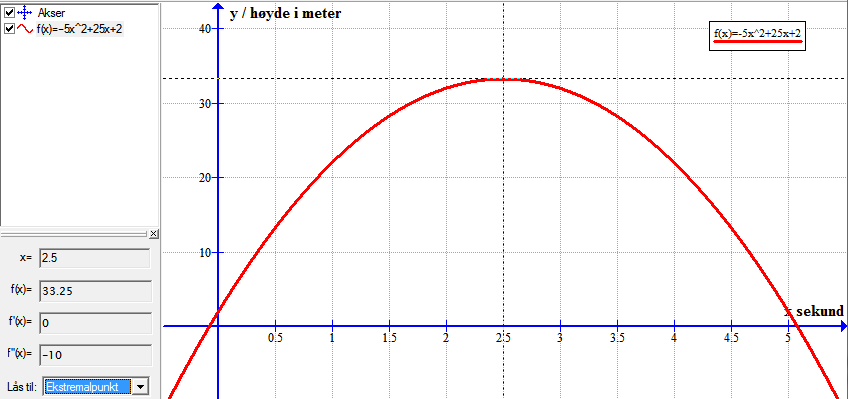
Bruker funksjonen: Beregn => "Lås til ekstremalpunkt" for å finne toppunktet.
Leser ut av grafen at ballen når sitt høyeste nivå etter 2.5 sekunder. Da er ballen 33.25 meter over bakken.
d)
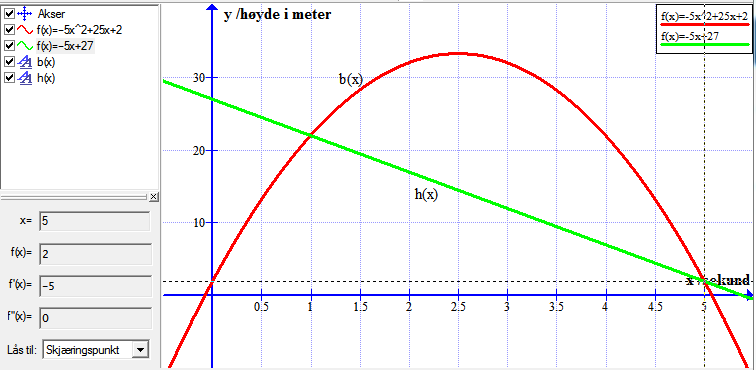
Bruker funksjonen: "Sett inn funksjon" for å tegne
Bruker funksjonen: Beregn => "Lås til skjæringspunkt" og klikker i nærheten av de to skjæringspunktene.
Leser ut av grafen at skjæringspunktene er
Skjæringspunkt 1:
Skjæringspunkt 2:
Oppgave 3
a)
Vinnertid 1968: 123.4
Vinnertid 2010:105,57
Vinnertiden sank med 14% fra 1968 til 2010.
b)
Bruker 2P-kalkulatoren. Funksjon: Verdiliste => Gjennomsnitt.
Gjennomsnitt1968: 125.06 sekunder
Gjennomsnitt 2010: 106.36 sekunder
Utregning for gjennomsnitt 1968 (ikke nødvendig å vise for å få full uttelling på oppgaven):
Finner summen av observasjonsverdiene:
Finner antall observasjoner:
Gjennomsnittet er da:
Utregning for gjennomsnitt 2010 (ikke nødvendig å vise for å få full uttelling på oppgaven):
Finner summen av observasjonsverdiene:
Finner antall observasjoner:
Gjennomsnittet er da:
c)
Bruker 2P-kalkulatoren. Funksjon: Verdiliste => Standardavvik.
Standardavvik 1968: 0.714 sekunder
Standardavvik 2010: 0.387 sekunder
Årsaken til at standardavviket er større i 1968 enn i 2010 er at det er større forskjell mellom de beste og de dårligste i 1968 enn i 2010. Det er er jevnere og høyere nivå i 2010. Det er spesielt 2 løpere som skiller seg ut i 1968: Kees Verkerk og Eduard Matusevitsj. Verkerk er mye bedre enn de andre, og Matusevitsj er mye dårligere enn de andre. Hvis vi fjerner disse to fra resultatlista, så vil forskjellen i standardavviket bli en del mindre.
Utregning for standardavvik 1968 (ikke nødvendig å vise): Finner først gjennomsnittet:
Finner summen av observasjonsverdiene:
Finner antall observasjoner:
Gjennomsnittet er da:
Bruker gjennomsnittet for å regne ut variansen:
| Verdi |
|
|---|---|
Variansen er:
Standardavviket er:
Utregning for standardavvik 2010 (ikke nødvendig å vise):
Finner først gjennomsnittet:
Finner summen av observasjonsverdiene:
Finner antall observasjoner:
Gjennomsnittet er da:
Bruker gjennomsnittet for å regne ut variansen
| Verdi |
|
|---|---|
Variansen er:
Bruker variansen for å regne ut standardavvik
Standardavviket er:
Oppgave 4
a)
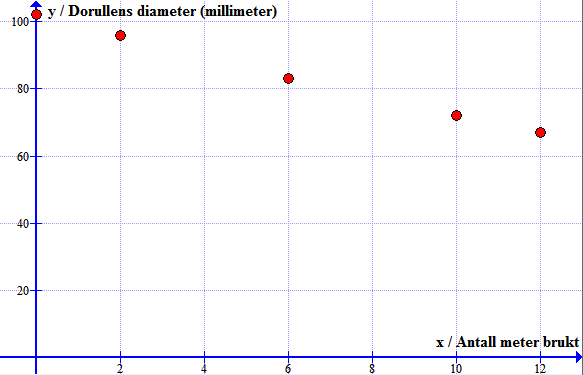
Bruker programmet Graph Bruker funksjonen: "Sett inn punktliste".
b)
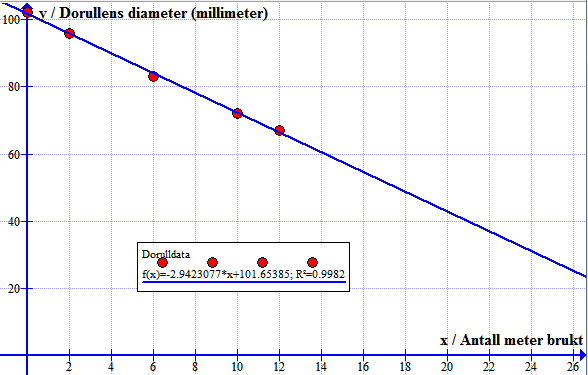
Bruker funksjonen: "Sett inn trendlinje" => Lineær.
Finner at funksjonen
c)
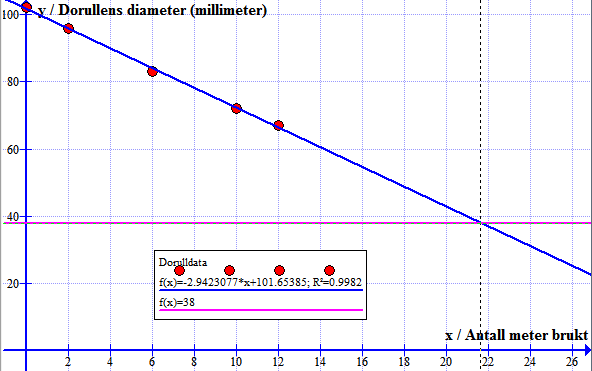
Bruker funksjonen: Sett inn funksjon y=38. Beregn => "lås til skjæringspunkt"
Ser at dorullen er tom når man har brukt 21.6 meter. Dorullen inneholder altså 21.6 meter papir.
d)
Modellen sier at det er 21.6 meter på rullen. Det som står på pakken og modellen stemmer altså godt.
Oppgave 5
a)
I en lineær modell synker verdien med et fast beløp hvert år. I oppgaven står det at det årlige verditapet er 25780 kr dermed er det en lineær modell. For å kontrollere kan vi se at fra 2006 til 2011 er det 5 år.
Modellen er:
b)
Løsningsalternativ 1
Forsøker meg fram på kalkulatoren for å finne det årlige verditapet. Vet at prisen etter 5 år er
Ser at vekstfaktoren som passer best er mellom 0.89 og 0.90. Bruker 0.89. Da er den prosentvise nedgangen på
Den eksponentielle modellen er da
Løsningsalternativ 2 Bruker Graph, og setter inn de to kjente punktene, og bruker så funksjonen "sett inn trendlinje" for å finne en eksponentialfunksjon som passer til observasjonene.
Den eksponentielle modellen er da
Løsningsalternativ 3
Den eksponentielle modellen er da
c)
Den lineære modellen:
Den eksponentielle modellen: