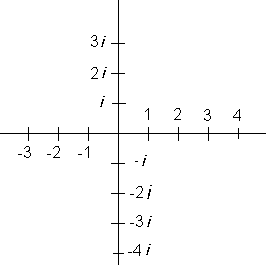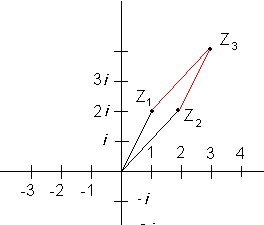Komplekse tall: Forskjell mellom sideversjoner
m Teksterstatting – «</tex>» til «</math>» |
|||
| (9 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
Z =a + ib er formen komplekse tall skrives på. a og b er reelle tall mens i er den imaginære enheten. < | Z =a + ib er formen komplekse tall skrives på. a og b er reelle tall mens i er den imaginære enheten. <math>i^2</math> er størrelsen som tilfredstiller | ||
< | <math> i^2= -1</math>. | ||
Kvadratroten av -1 = i. Det betyr at andregradslikninger alltid har en løsning innenfor denne tallmengden. | Kvadratroten av -1 = i. Det betyr at andregradslikninger alltid har en løsning innenfor denne tallmengden. | ||
| Linje 16: | Linje 16: | ||
Potenser av < | Potenser av <math>i^n</math> kan alltid reduseres til pluss/minus 1 eller pluss/minus i. Eksempelvis er <math>i^3 = i^2 \cdot i = -1 \cdot i = - i</math> | ||
Summering av to komplekse tall gjøres ved å summere realdelen for seg og imaginærdelen for seg. Dersom vi skal summere | Summering av to komplekse tall gjøres ved å summere realdelen for seg og imaginærdelen for seg. Dersom vi skal summere <math>Z_1 = 1 + 2i \quad og \quad Z_2 = 2 + 2i</math> blir resultatet <math>Z_3 = 3 + 4i</math> | ||
Generelt kan summen av det komplekse tallene Z = a + ib og W = c + id uttrykkes som | Generelt kan summen av det komplekse tallene Z = a + ib og W = c + id uttrykkes som | ||
| Linje 28: | Linje 28: | ||
[[Bilde:Kompleksplan2.gif]] | [[Bilde:Kompleksplan2.gif]] | ||
Lengden av linjestykket | Lengden av linjestykket <math>OZ_n</math> kan vi finne ved å bruke Pytagoras. Lengden er gitt ved <math>|Z_n| = \sqrt{a^2 + b^2}</math>. <math>|Z_n|</math> kalles absoluttverdien eller modulen av det komplekse tallet <math>Z_n</math> | ||
Subtraksjon utføres ved å subtrahere realdelen for seg og imaginærdelen for seg, altså analogt til addisjon. Generelt har vi | Subtraksjon utføres ved å subtrahere realdelen for seg og imaginærdelen for seg, altså analogt til addisjon. Generelt har vi | ||
| Linje 34: | Linje 34: | ||
Z - W = (a - c) + i(b - d) | Z - W = (a - c) + i(b - d) | ||
Vi kan oppgi det komplekse tallet som et produkt av lengden | Vi kan oppgi det komplekse tallet som et produkt av lengden <math>OZ_n</math> og vinkelen mellom X aksen og linjestykket <math>OZ_n</math>. | ||
[[Bilde:Kompleks3.gif]] | [[Bilde:Kompleks3.gif]] | ||
| Linje 42: | Linje 42: | ||
Z = r(cos θ + isin θ). θ kalles argumentet til Z og skrives arg Z. Argumentet til Z er entydig bestemt i [0,2π > | Z = r(cos θ + isin θ). θ kalles argumentet til Z og skrives arg Z. Argumentet til Z er entydig bestemt i [0,2π > | ||
punktet kalles det konjugerte komplekse tallet til Z. | punktet <math> \overline{Z}= a-bi</math> kalles det konjugerte komplekse tallet til Z. | ||
en viktig egenskap er: | en viktig egenskap er:<p></p> | ||
<math>Z \cdot \overline{Z} = a^2 + b^2 =|Z|^2</math> | |||
'''Multiplikasjon.'''<p></p> | |||
Multiplikasjon utføres på vanlig måte: <p></p><math>(a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i</math> | |||
Multiplikasjon utføres på vanlig måte: (a + bi)(c + di) = ac + adi + bci + | <p></p> | ||
'''Divisjon.'''<p></p> | |||
Divisjon. Vi multipliserer teller og nevner med det konjugerte komplekse tallet til nevneren. Da får vi et reelt tall i nevneren: | Vi multipliserer teller og nevner med det konjugerte komplekse tallet til nevneren. Da får vi et reelt tall i nevneren:<p></p> | ||
< | <math>\frac{a+bi}{c+di} = \frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac {ac-adi +bci -bdi^2}{c^2 -cdi + cdi -d^2i^2}= \frac {ac+bd -(ad-bc)i}{c^2 + d^2}</math> | ||
---- | |||
[[X Hovedside | Tilbake til X hovedside]] | |||
---- | ---- | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Siste sideversjon per 5. feb. 2013 kl. 20:58
Z =a + ib er formen komplekse tall skrives på. a og b er reelle tall mens i er den imaginære enheten. <math>i^2</math> er størrelsen som tilfredstiller <math> i^2= -1</math>.
Kvadratroten av -1 = i. Det betyr at andregradslikninger alltid har en løsning innenfor denne tallmengden.
a kalles for realdelen og skrives ofte a = Re(Z), b kalles for imaginærdelen og skrives ofte b = Im(Z).
Mengden av alle komplekse tall kalles for C. De reelle tallene er inkludert i C.
For å visualisere de komplekse tallene kan vi bruke XY planet. Vi setter a =X og b = Y. Det komplekse planet C ser da slik ut:
REGNEREGLER FOR KOMPLEKSE TALL
Potenser av <math>i^n</math> kan alltid reduseres til pluss/minus 1 eller pluss/minus i. Eksempelvis er <math>i^3 = i^2 \cdot i = -1 \cdot i = - i</math>
Summering av to komplekse tall gjøres ved å summere realdelen for seg og imaginærdelen for seg. Dersom vi skal summere <math>Z_1 = 1 + 2i \quad og \quad Z_2 = 2 + 2i</math> blir resultatet <math>Z_3 = 3 + 4i</math>
Generelt kan summen av det komplekse tallene Z = a + ib og W = c + id uttrykkes som
Z + W = (a + c) + i(b + d).
Vi kan oppfatte de komplekse tallene som vektorer i det komplekse plan. Regneoperasjonen over kan da fremstilles slik;
Lengden av linjestykket <math>OZ_n</math> kan vi finne ved å bruke Pytagoras. Lengden er gitt ved <math>|Z_n| = \sqrt{a^2 + b^2}</math>. <math>|Z_n|</math> kalles absoluttverdien eller modulen av det komplekse tallet <math>Z_n</math>
Subtraksjon utføres ved å subtrahere realdelen for seg og imaginærdelen for seg, altså analogt til addisjon. Generelt har vi
Z - W = (a - c) + i(b - d)
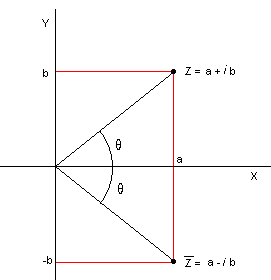
Vi kan oppgi det komplekse tallet som et produkt av lengden <math>OZ_n</math> og vinkelen mellom X aksen og linjestykket <math>OZ_n</math>.
Fra figuren over ser vi at Z kan utrykkes som lengden av OZ og θ. Dersom vi kaller absoluttverdien av Z for r får vi :
Z = r(cos θ + isin θ). θ kalles argumentet til Z og skrives arg Z. Argumentet til Z er entydig bestemt i [0,2π >
punktet <math> \overline{Z}= a-bi</math> kalles det konjugerte komplekse tallet til Z.
en viktig egenskap er:
<math>Z \cdot \overline{Z} = a^2 + b^2 =|Z|^2</math>
Multiplikasjon.
Multiplikasjon utføres på vanlig måte:
<math>(a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i</math>
Divisjon.
Vi multipliserer teller og nevner med det konjugerte komplekse tallet til nevneren. Da får vi et reelt tall i nevneren:
<math>\frac{a+bi}{c+di} = \frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac {ac-adi +bci -bdi^2}{c^2 -cdi + cdi -d^2i^2}= \frac {ac+bd -(ad-bc)i}{c^2 + d^2}</math>