2P 2023 Vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (23 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 4: | Linje 4: | ||
[https://matematikk.net/matteprat/download/file.php?id=4707 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | [https://matematikk.net/matteprat/download/file.php?id=4707 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | ||
[https://kublakanutdanning.no/eksamen-2p-var-2023/ Videoløsning av KublaKan Utdanning] | |||
| Linje 19: | Linje 22: | ||
Prisstigning brød:$\frac{42}{40} = 1,05$ som tilsvarer 5% økning. | Prisstigning brød:$\frac{42}{40} = 1,05$ som tilsvarer 5% økning. | ||
Prisindeks 2017 - 2019 har økt med: | |||
$109,2-104,5=4,7$ prosentpoeng | |||
Forskjellen er 4,7 og basis er 104,5 det betyr at endringen blir mindre enn 5%, hvilket betyr at prisen på dette brødet øker mer enn prisindeksen på brød generelt. | |||
===Oppgave 2=== | ===Oppgave 2=== | ||
| Linje 36: | Linje 42: | ||
$\frac{A_2}{A_1} = \frac{2gh}{\frac{gh}{2}} = 4 $ | $\frac{A_2}{A_1} = \frac{2gh}{\frac{gh}{2}} = 4 $ | ||
===Oppgave 3 | ===Oppgave 3=== | ||
Dersom den prosentvise prisstigningen er større enn den prosentvise lønnsøkningen får man mindre for lønna si, man får redusert kjøpekraft. Dette tar reallønna hensyn til. Den nominelle lønna er det du får utbetalt fra arbeidsgiver. Dersom prisstigningen i perioden har vært mindre enn 16% kan Truls være fornøyd fordi han da har fått økt kjøpekraft. Sammenhengen mellom nominell lønn og reallønn er: | Dersom den prosentvise prisstigningen er større enn den prosentvise lønnsøkningen får man mindre for lønna si, man får redusert kjøpekraft. Dette tar reallønna hensyn til. Den nominelle lønna er det du får utbetalt fra arbeidsgiver. Dersom prisstigningen i perioden har vært mindre enn 16% kan Truls være fornøyd fordi han da har fått økt kjøpekraft. Sammenhengen mellom nominell lønn og reallønn er: | ||
| Linje 43: | Linje 49: | ||
$ Reallønn = nominellønn \cdot kroneverdi = lønn \cdot \frac{100}{indeks}$ | $ Reallønn = nominellønn \cdot kroneverdi = lønn \cdot \frac{100}{indeks}$ | ||
===Oppgave 4 | ===Oppgave 4=== | ||
Den grønne grafen med stigningstall 1 og konstantledd 1 er grafen til f. | |||
Den grå/lilla grafen er grafen til andregradsfunksjonen g. | |||
Den blå grafen med stigningstall -1 og konstantledd 5 er grafen til h. | |||
====a)==== | ====a)==== | ||
En likning som har to løsninger er for eksempel: | |||
f | $f(x) = g(x)$ | ||
det vil si | |||
$x+1 = x^2-4x+5$ | |||
Vi ser at grafene krysser hverandre for x = 1 og x = 4 | Vi ser at grafene krysser hverandre for x = 1 og x = 4 | ||
====b)==== | ====b)==== | ||
En ulikhet som bare har positive løsninger er: | |||
$f(x) > | $f(x) > g(x) $ | ||
det vil si | |||
$x> | $x+1 > x^2-4x+5$ | ||
Vi ser at grafen til f | Vi ser at grafen til f har større funksjonsverdi enn grafen til g for alle x mellom 1 og 4. | ||
Løsningen er: $1<x<4$ | |||
==DEL TO== | ==DEL TO== | ||
| Linje 77: | Linje 93: | ||
$3x + y = 1046 $ | $3x + y = 1046 $ | ||
[[File:28082023- | Figuren viser løsning med CAS i geogebra: | ||
[[File:28082023-03.png]] | |||
===Oppgave 2=== | |||
Bruker Excel til å beregne gjennomsnittet. Jeg kan da endre på tallet som var bak kaffeflekken, og se hvordan det påvirker gjennomsnittet. | |||
[[File: | [[File: 2PY-V23-del2-2.png]] | ||
Figuren viser | Figuren viser at dersom vedkommende drikker 2 kopper kaffe blir gjennomsnittet akkurat 4. | ||
Gjennomsnittet blir større enn 4 dersom tallet som skjuler seg bak flekken er 3 eller større. | |||
===Oppgave 3=== | |||
Samlet vekstfaktor for vare A om tre måneder: $1,07^3 = 1,225$ det vil si at prisen vil være 22,5 % høyere om tre måneder enn den er nå. | |||
Samlet vekstfaktor for vare B for tre måneder siden: $0,93^{-3} = 1,243$ det vil si at prisen var 24,3 % høyere for tre måneder siden enn den er nå. | |||
Malins påstand er altså ikke riktig. | |||
===Oppgave 4=== | ===Oppgave 4=== | ||
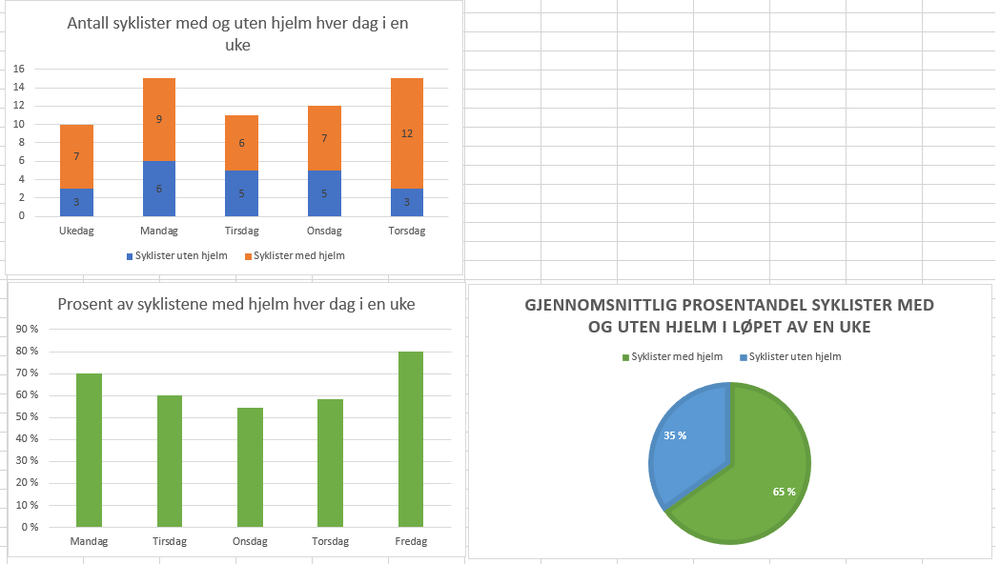
[[File: 2P_V23_del2_oppgave4.png | 1000px]] | |||
[[File: 2P_V23_del2_oppgave4b.png | 1000px]] | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
====a)==== | |||
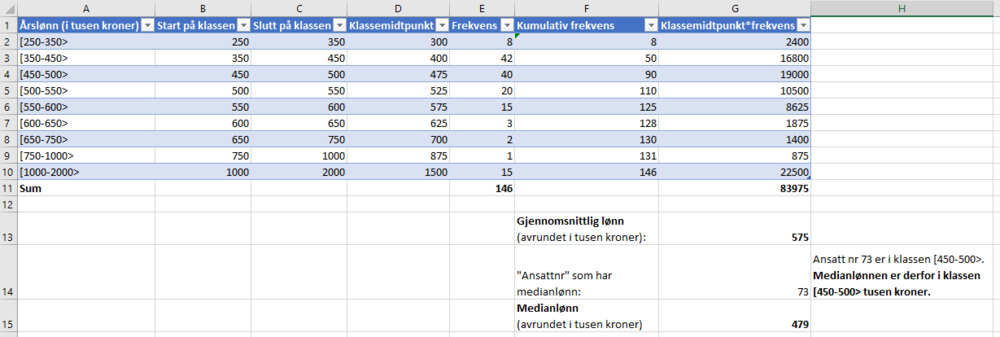
Bruker Excel til å beregne gjennomsnitt og median. | |||
[[File: 2P_V23_del2_oppg5.png|1000px]] | |||
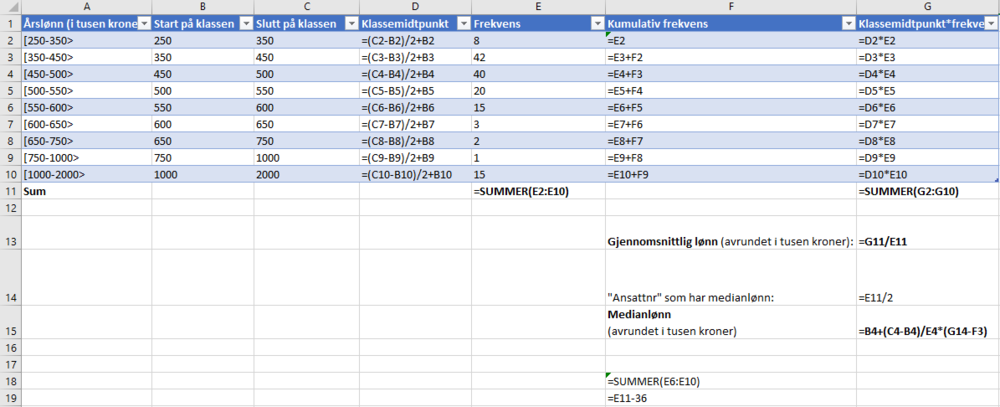
Med formler: | |||
[[File: 2P_V23_del2_oppg5b2.png | 1000 px]] | |||
====b)==== | |||
Gjennomsnittslønnen er ca. 575 000 kr, mens medianlønnen er ca. 479 000 kr. | |||
Gjennomsnittslønnen "dras opp" av de 15 ansatte med lønn over 1 million kr. Vi ser i tabellen at kun 36 ansatte har lønn over 550 000 kr, mens 110 ansatte har lønn under 550 000 kr. De vil si at de aller fleste har lønn under gjennomsnittet. | |||
Medianlønnen forteller oss at halvparten av de ansatte har lønn under eller lik 479 000 kr. Sånn sett representerer medianlønnen de ansattes lønn best. | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
For et rektangel har vi at arealet A = lengde*bredde. | |||
Vekstfaktor for å øke lengden med en gitt prosentandel: $1+\frac{p}{100}$ | |||
Vekstfaktor for å minke bredden med en gitt prosentandel: $1-\frac{p}{100}$ | |||
Samlet vekstfaktor for arealet: $(1+\frac{p}{100})\cdot(1-\frac{p}{100}) = 1-\frac{p}{100}+\frac{p}{100}-\frac{p^2}{10000}=1-\frac{p^2}{10000}$ | |||
Vi ser at den samlede vekstfaktoren for arealet blir mindre enn 1, uansett hvilken prosentandel vi velger. Arealet av den nye parkeringsplassen vil altså bli mindre uansett prosentandel. | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
====a)==== | |||
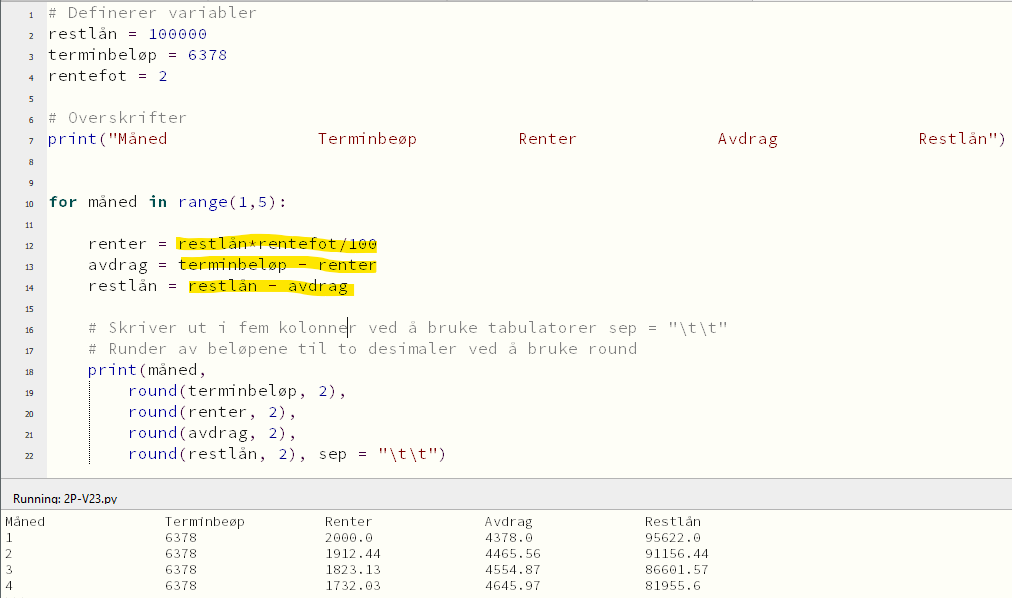
Siden terminbeløpet er likt hver måned, er det et annuitetslån. Jeg setter inn riktige formler i linje 12, 13 og 14 og kjører programmet. | |||
[[File: 2P_V23_del2_7a.png]] | |||
====b)==== | |||
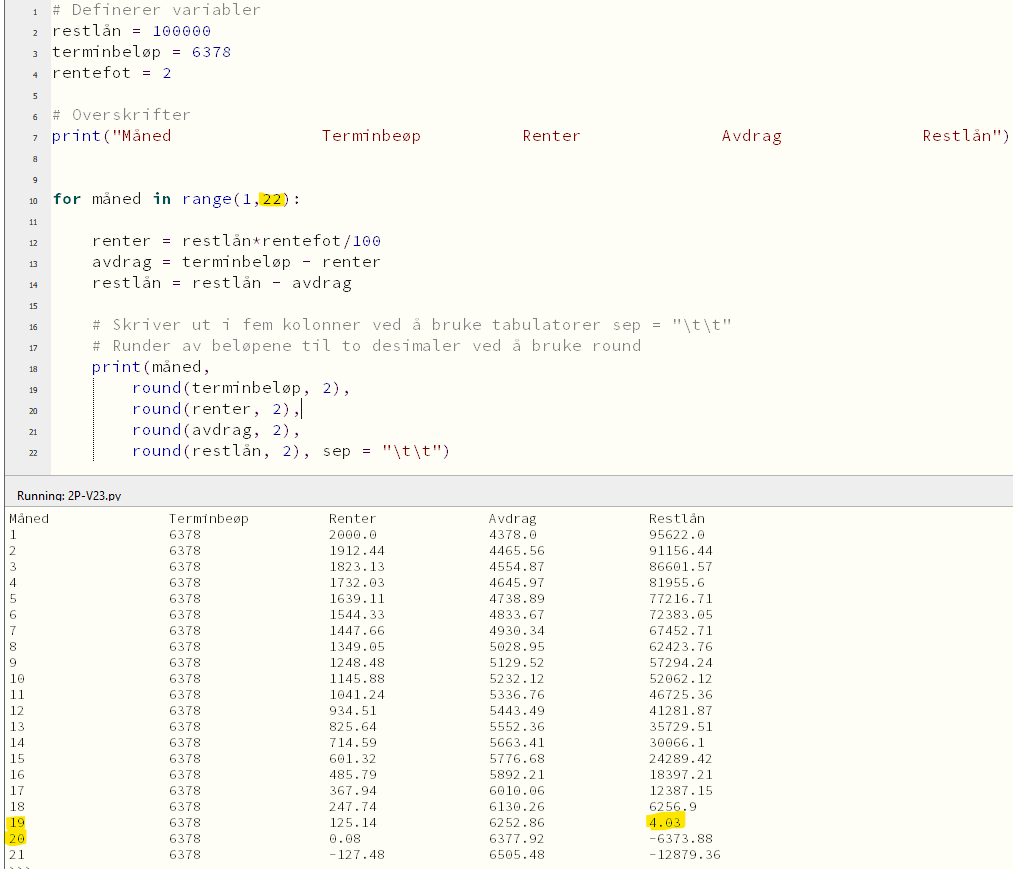
Jeg endrer antall måneder som skrives ut i for-løkken på linje 10. Jeg må bare prøve meg frem, og skriver ut 22 måneder. | |||
Jeg ser at etter 19 måneder er det bare 4 kroner igjen av lånet, så jeg vil anse det som nedbetalt da. | |||
[[File: 2P_V23_del2_7b.png]] | |||
Siste sideversjon per 26. nov. 2024 kl. 08:39
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsning av KublaKan Utdanning
DEL EN
Oppgave 1
a)
En økning fra 100 til 113,3 tilsvarer 13,3% : $\frac{113,3}{100} = 1,133 $ som er vekstfaktoren til 13,3 prosent økning.
b)
Prisstigning brød:$\frac{42}{40} = 1,05$ som tilsvarer 5% økning.
Prisindeks 2017 - 2019 har økt med:
$109,2-104,5=4,7$ prosentpoeng
Forskjellen er 4,7 og basis er 104,5 det betyr at endringen blir mindre enn 5%, hvilket betyr at prisen på dette brødet øker mer enn prisindeksen på brød generelt.
Oppgave 2
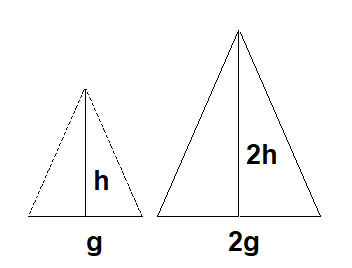
Dersom en trekant a har fire ganger arealet av trekant b og er formlik må både grunnlinje og høyde i a være dobbelt så lang/høy som i trekant b.
$A_1 = \frac{gh}{2}$
$A_2 = \frac{2g \cdot 2h}{2} = 2gh$
$\frac{A_2}{A_1} = \frac{2gh}{\frac{gh}{2}} = 4 $
Oppgave 3
Dersom den prosentvise prisstigningen er større enn den prosentvise lønnsøkningen får man mindre for lønna si, man får redusert kjøpekraft. Dette tar reallønna hensyn til. Den nominelle lønna er det du får utbetalt fra arbeidsgiver. Dersom prisstigningen i perioden har vært mindre enn 16% kan Truls være fornøyd fordi han da har fått økt kjøpekraft. Sammenhengen mellom nominell lønn og reallønn er:
$ Reallønn = nominellønn \cdot kroneverdi = lønn \cdot \frac{100}{indeks}$
Oppgave 4
Den grønne grafen med stigningstall 1 og konstantledd 1 er grafen til f.
Den grå/lilla grafen er grafen til andregradsfunksjonen g.
Den blå grafen med stigningstall -1 og konstantledd 5 er grafen til h.
a)
En likning som har to løsninger er for eksempel:
$f(x) = g(x)$
det vil si
$x+1 = x^2-4x+5$
Vi ser at grafene krysser hverandre for x = 1 og x = 4
b)
En ulikhet som bare har positive løsninger er:
$f(x) > g(x) $
det vil si
$x+1 > x^2-4x+5$
Vi ser at grafen til f har større funksjonsverdi enn grafen til g for alle x mellom 1 og 4.
Løsningen er: $1<x<4$
DEL TO
Oppgave 1
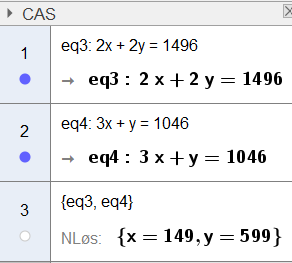
Vi stiller opp to likninger fra figurene: x er prisen på t-skjorte, og y er prisen på bukser.
$2x + 2y = 1496 $
$3x + y = 1046 $
Figuren viser løsning med CAS i geogebra:
Oppgave 2
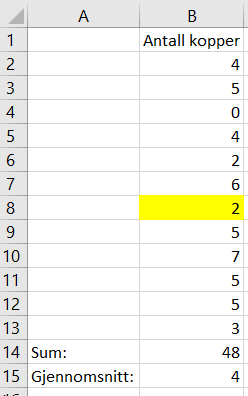
Bruker Excel til å beregne gjennomsnittet. Jeg kan da endre på tallet som var bak kaffeflekken, og se hvordan det påvirker gjennomsnittet.
Figuren viser at dersom vedkommende drikker 2 kopper kaffe blir gjennomsnittet akkurat 4.
Gjennomsnittet blir større enn 4 dersom tallet som skjuler seg bak flekken er 3 eller større.
Oppgave 3
Samlet vekstfaktor for vare A om tre måneder: $1,07^3 = 1,225$ det vil si at prisen vil være 22,5 % høyere om tre måneder enn den er nå.
Samlet vekstfaktor for vare B for tre måneder siden: $0,93^{-3} = 1,243$ det vil si at prisen var 24,3 % høyere for tre måneder siden enn den er nå.
Malins påstand er altså ikke riktig.
Oppgave 4
Oppgave 5
a)
Bruker Excel til å beregne gjennomsnitt og median.
Med formler:
b)
Gjennomsnittslønnen er ca. 575 000 kr, mens medianlønnen er ca. 479 000 kr.
Gjennomsnittslønnen "dras opp" av de 15 ansatte med lønn over 1 million kr. Vi ser i tabellen at kun 36 ansatte har lønn over 550 000 kr, mens 110 ansatte har lønn under 550 000 kr. De vil si at de aller fleste har lønn under gjennomsnittet.
Medianlønnen forteller oss at halvparten av de ansatte har lønn under eller lik 479 000 kr. Sånn sett representerer medianlønnen de ansattes lønn best.
Oppgave 6
For et rektangel har vi at arealet A = lengde*bredde.
Vekstfaktor for å øke lengden med en gitt prosentandel: $1+\frac{p}{100}$
Vekstfaktor for å minke bredden med en gitt prosentandel: $1-\frac{p}{100}$
Samlet vekstfaktor for arealet: $(1+\frac{p}{100})\cdot(1-\frac{p}{100}) = 1-\frac{p}{100}+\frac{p}{100}-\frac{p^2}{10000}=1-\frac{p^2}{10000}$
Vi ser at den samlede vekstfaktoren for arealet blir mindre enn 1, uansett hvilken prosentandel vi velger. Arealet av den nye parkeringsplassen vil altså bli mindre uansett prosentandel.
Oppgave 7
a)
Siden terminbeløpet er likt hver måned, er det et annuitetslån. Jeg setter inn riktige formler i linje 12, 13 og 14 og kjører programmet.
b)
Jeg endrer antall måneder som skrives ut i for-løkken på linje 10. Jeg må bare prøve meg frem, og skriver ut 22 måneder.
Jeg ser at etter 19 måneder er det bare 4 kroner igjen av lånet, så jeg vil anse det som nedbetalt da.