Funksjoner II: Forskjell mellom sideversjoner
| (23 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 71: | Linje 71: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel | '''Eksempel 3:''' | ||
[[File:19072024-01.png|400px]] | [[File:19072024-01.png|400px]] | ||
| Linje 81: | Linje 81: | ||
===Den deriverte til inverse funksjoner=== | ===Den deriverte til inverse funksjoner=== | ||
Dersom vi kjenner den omvendte funksjonen kan vi derivere den på vanlig måte. Dersom vi ikke kjenner den omvendte funksjonen kan vi | Dersom vi kjenner den omvendte funksjonen kan vi derivere den på vanlig måte. Dersom vi ikke kjenner den omvendte funksjonen kan vi allikevel finne den deriverte i et punkt, ved å gå veien om den deriverte til funksjonen. | ||
| Linje 97: | Linje 97: | ||
Det kan være umulig å finne g, men vi kan fortsatt finne den deriverte til g i et punkt. | Det kan være umulig å finne g, men vi kan fortsatt finne den deriverte til g i et punkt. | ||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 4:''' | |||
Vi ser på funksjonen $f(x) = x^2, \quad x \in [0,2]$ Vi ønsker å finne den deriverte til den omvendte funksjonen g(x), for x=3. Da må vi først finne den x verdi som gir f(x)=3, husk at g sin definisjonsmengde er f sin verdimengde. f(x) = 3 gir x = 1,732. Vi bruker formelen for derivasjon av den omvendte funksjonen: | |||
$g'(3) = \frac{1}{f'(1,732)}= \frac{1}{2 \cdot 1,732} = 0,288$. | |||
[[File: 20072024-01.png|500px]] | |||
Vi observerer at dette stemmer godt med grafene i figuren. Det er kanskje ikke så overraskende siden vi har symmetri om y=x, ikke bare for grafene til f og g, men også for korresponderende tangenter. | |||
</div> | </div> | ||
| Linje 125: | Linje 141: | ||
$|a| \geq 0$ | $|a| \geq 0$ | ||
$|a| = 0 \Leftrightarrow a=0$ | |||
$|ab|= |a|\cdot|b|$ | |||
$|\frac ab | = \frac {|a|}{|b|}, \quad \quad b \neq 0$ | |||
$|-a| = |a|$ | |||
$|a| \leq b \Leftrightarrow \quad -b \leq a \leq b$ | |||
$|a| \geq b \Leftrightarrow \quad a \leq -b$ eller $a \geq b$ | |||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 5:''' | |||
Fuksjonen absoluttverdien av x skrives slik: | |||
\[ f(x)= |x| = \begin{cases} | |||
\quad x,\quad x\geq 0 \\ | |||
\, \quad -x,\quad x < 0 \\ | |||
\end{cases} \] | |||
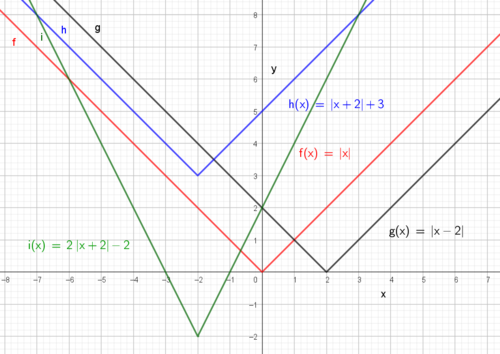
Den røde grafen viser funksjonen. Vi observerer at den knekker i origo og danner 45 grader med x og y aksen. La oss se hvordan den kan påvirkes. | |||
[[File:21072024-01.png|500px]] | |||
|x - a| gir knekkpunktet a enheter til høyre for origo (y-aksen). | x + b | skyver knekkpunktet b enheter til venstre for origo. Fortsatt ligger knekkpunktet på x- aksen. | |||
\<div> | |x| + a flytter knekkpunktet til a enheter over aksen, |x| - b flytter det b enheter under x - aksen. | ||
Vi finner nullpunktene til i(x): | |||
$i(x)=0$ | |||
$2|x+2|-2=0$ | |||
$|x+2|=1$ | |||
$x+2 = 1 \vee -(x+2)=1$ | |||
$x= -1 \vee x = -3$ | |||
</div> | |||
Siste sideversjon per 21. jul. 2024 kl. 17:32
Omvendte funksjoner
Vi har en funksjon $f(x) = 0,25x$ Dersom vi setter inn x = 4 får vi funksjonsverdien 1. Vi har altså gått fra verdien 4 i definisjonsmengden til verdien 1 i verdimengden. En funksjon som tar oss tilbake fra 1 til 4 vil være en omvendt funksjon til f. Den ser slik ut: $f^{-1}(x) = 4x.$ Det som er definisjonsmengden til $f$ blir verdimengden til $f^{-1}$. $f$ og $f^{-1}$ er omvendte eller inverse funksjoner.
$f^{-1}(f(x)) = x$
Funksjonens definisjonsmengde blir den inverse funksjonens verdimengde.
Funksjonens verdimengde blir den inverse funksjonens definisjonsmengde.
Hvordan finne vi så den omvendte funksjonen? (bruker funksjonen over)
$f(x)= y$
$y = 0,25x$
$x= \frac{y}{0,25}$
$x = 4y$
$f^{-1} (y) = 4y$
$f^{-1} (x) = 4x$
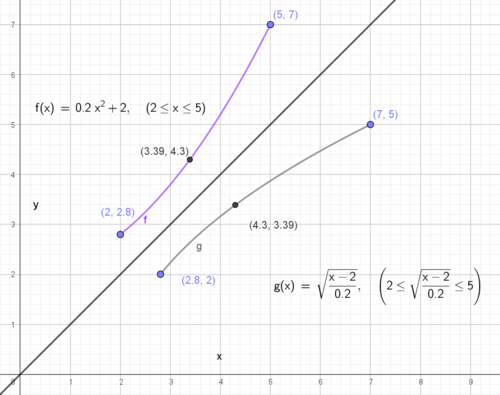
Eksempel 1:
f og g er omvendte funksjoner. Man observere at de speiler hverandre om linjen y = x. Vi observerer også at x koordinaten til f blir y koordinaten til g, i tilsvarende punkt på respektive grafer. Det som er definisjonsmengden til den ene funksjonen er verdimengden til den andre.
Geogebra: man finner den omvendte funksjonen til f ved å skrive invers(f).
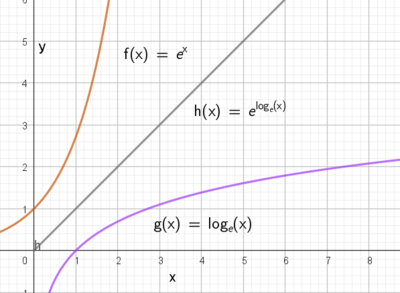
Eksempel 2:
$f(x) = e^x$ og $g(x) = ln(x)$ er omvedte funksjoner. ( $ln(x) = log_e(x)$)
$h(x) = f(g(x)) = e^{ln(x)}= x $ (definisjon).
Setter vi f inn i g får vi $g(f(x))= ln(e^x)= x \cdot ln(e) = x \cdot 1 = x$.
$e^x$ og $\ln(x)$ er inverse funksjoner.
En- entydig
En funksjon er en- entydig dersom:
$x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2) $ for alle $x_1, x_2 \in \mathbb{D}_f$
En funksjon f har en omvendt funksjon hvis og bare hvis den er entydig.
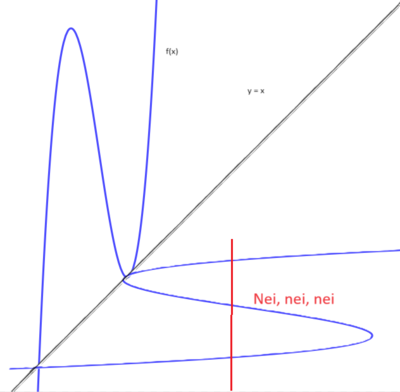
Eksempel 3:
Vi ser at når f(x) speiles om linjen y=x får vi en kurve som ikke tilfredsstiller kravene til en funksjon, fordi en x verdi krysser kurven i mer enn ett sted. f(x) er ikke en- entydig i definisjonsområdet og har derfor ingen omvendt funksjon.
Den deriverte til inverse funksjoner
Dersom vi kjenner den omvendte funksjonen kan vi derivere den på vanlig måte. Dersom vi ikke kjenner den omvendte funksjonen kan vi allikevel finne den deriverte i et punkt, ved å gå veien om den deriverte til funksjonen.
g(x) er den omvendte funksjonen til f(x):
$g(f(x)) = x$
$(g(f(x)))' = x'\quad$ Bruker kjerneregel på venstre side
$g'(f(x)) f'(x) = 1$
$g'(f(x)) = \frac{1}{f'(x)}$
Det kan være umulig å finne g, men vi kan fortsatt finne den deriverte til g i et punkt.
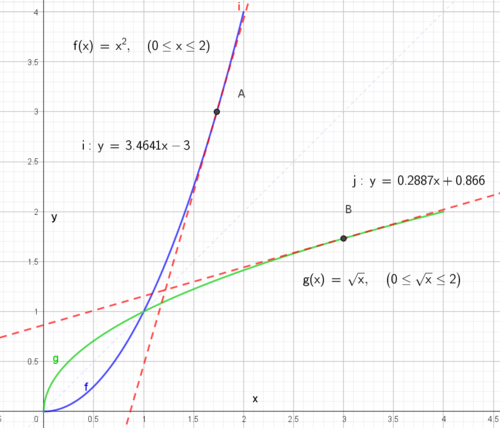
Eksempel 4:
Vi ser på funksjonen $f(x) = x^2, \quad x \in [0,2]$ Vi ønsker å finne den deriverte til den omvendte funksjonen g(x), for x=3. Da må vi først finne den x verdi som gir f(x)=3, husk at g sin definisjonsmengde er f sin verdimengde. f(x) = 3 gir x = 1,732. Vi bruker formelen for derivasjon av den omvendte funksjonen:
$g'(3) = \frac{1}{f'(1,732)}= \frac{1}{2 \cdot 1,732} = 0,288$.
Vi observerer at dette stemmer godt med grafene i figuren. Det er kanskje ikke så overraskende siden vi har symmetri om y=x, ikke bare for grafene til f og g, men også for korresponderende tangenter.
Absoluttverdifunksjoner
Absoluttverdi
Absoluttverdien er den positive verdien av uttrykket. Symbolet er vertikale "stolper". |3| = 3. Absoluttverdien av 3 er 3. |-3| = 3. Absoluttverdien av -3 er også 3. Man kan se på absoluttverdien som avstanden fra null, på tallinjen. Absoluttverdien sier noe om verdien, men ikke om retningen.
Absoluttverdi i den virkelige verden
Absoluttverdi er ikke en kunstig matematisk konstruksjon, men har en praktisk nytteverdi.
Mekanisk produksjon: Dersom du skal dreie en aksling til en maskin er det viktig at dimensjonen blir riktig. Dersom kunden ønsker at akslingen har en diameter på 100 mm. Kan det tenkes at du får denne beskrivelsen: |x-100|<0.1. Det betyr at akslingen kan ha et avvik på $\pm 0.1$ mm, altså må den være mellom 99,90 mm. og 100,10 mm.
Modellering Temperaturen i morgen blir mellom 12 og 16 grader: $|t-14|\leq 2$
Dette var bare to av mange praktiske anvendelser.
Noen viktige egenskaper:
$|a| \geq 0$
$|a| = 0 \Leftrightarrow a=0$
$|ab|= |a|\cdot|b|$
$|\frac ab | = \frac {|a|}{|b|}, \quad \quad b \neq 0$
$|-a| = |a|$
$|a| \leq b \Leftrightarrow \quad -b \leq a \leq b$
$|a| \geq b \Leftrightarrow \quad a \leq -b$ eller $a \geq b$
Eksempel 5:
Fuksjonen absoluttverdien av x skrives slik:
\[ f(x)= |x| = \begin{cases}
\quad x,\quad x\geq 0 \\
\, \quad -x,\quad x < 0 \\
\end{cases} \]
Den røde grafen viser funksjonen. Vi observerer at den knekker i origo og danner 45 grader med x og y aksen. La oss se hvordan den kan påvirkes.
|x - a| gir knekkpunktet a enheter til høyre for origo (y-aksen). | x + b | skyver knekkpunktet b enheter til venstre for origo. Fortsatt ligger knekkpunktet på x- aksen.
|x| + a flytter knekkpunktet til a enheter over aksen, |x| - b flytter det b enheter under x - aksen.
Vi finner nullpunktene til i(x):
$i(x)=0$
$2|x+2|-2=0$
$|x+2|=1$
$x+2 = 1 \vee -(x+2)=1$
$x= -1 \vee x = -3$