1T 2022 vår LK20 LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (20 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 2: | Linje 2: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=53910 Diskusjon av oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=53910 Diskusjon av oppgaven på matteprat] | ||
[https://www.youtube.com/watch?v=EVg396wJmOU Videoløsning av UDL.no] | |||
[https://matematikk.net/matteprat/download/file.php?id=4302 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | [https://matematikk.net/matteprat/download/file.php?id=4302 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | ||
| Linje 8: | Linje 10: | ||
[https://youtu.be/3gTmQ8iWjUk Videoløsning del 2 av Lektor Lainz] | [https://youtu.be/3gTmQ8iWjUk Videoløsning del 2 av Lektor Lainz] | ||
[https://youtu.be/v81gOpRjBCI Videoløsn. del 1 av matematikk.net] | |||
| Linje 28: | Linje 32: | ||
[[File:29082022- | [[File:29082022-05.png]] | ||
===Oppgave 2=== | ===Oppgave 2=== | ||
| Linje 48: | Linje 52: | ||
===Oppgave 4=== | ===Oppgave 4=== | ||
Først defineres en funksjon f som kvadrerer x. | |||
Så løper løkken gjennom tallene 1,2,3 osv. Disse kvadreres og printes. Når verdien til kvadratet når 400 stopper programmet. | |||
Programmet printer ut kvadrattallene | |||
Programmet printer ut de 20 første kvadrattallene. | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
| Linje 75: | Linje 84: | ||
==Oppgave 1== | ==Oppgave 1== | ||
Løser oppgaven i Geogebra. | |||
[[File: 1P_V22_del2_1abcd.png | 1000px]] | |||
===a)=== | |||
$V(0)=0$ (se algebrafeltet på skjermbildet). Det vil si at før tappingen starter (ved 0 minutter), så har det ikke blitt tappet ut noe vann av tanken (0 liter). | |||
===b)=== | |||
Verdimengden til V er 2000. Jeg fant høyeste punkt på grafen, A=(40,2000), ved å bruke knappen "Ekstremalpunkt". Laveste punkt er (0,0). Verdimengden er da 2000 - 0 = 2000. | |||
===c)=== | |||
Lager linjen y = 1000, og bruker knappen "skjæring mellom to objekt" mellom linjen og grafen til V. Får punkt B=(11.7, 1000). Det vil si at det tar 11,7 minutter før halvparten av vannet er tappet ut av tanken. Se punkt B. | |||
===d)=== | |||
Lager punkt C=(0,V(0)) og D=(30,V(30)), og lager en linje som gå gjennom disse to punktene med knappen "linje". Finner stigningstallet til linjen med knappen "stigning". Stigningstallet er 62,5 (se verdien a1 i algebrafeltet). Svaret forteller oss at fra 0 til 30 minutter etter at tappingen har startet, tappes vannet med en gjennomsnittlig fart på 62,5 liter per minutt. | |||
===e)=== | |||
[[File: 1P_V22_del2_1e.png | 1000px]] | |||
Lager en glider b med kommandoen "glider(0,40,1)". Lager et punkt E=(b,V(b)) og tangenten til V i punktet E med knappen "tangenter". Viser stigningstallet til tangenten med knappen "stigning". Flytter på glideren slik at punkt E flytter seg langs hele grafen til V, og ser om stigningstallet noen gang overstiger 105. Jeg finner at det høyeste stigningstallet er 100, når E=(0,0). Se verdien a2 i algebrafeltet. | |||
Det vil altså aldri tappes mer enn 105 liter i løpet av ett minutt. | |||
==Oppgave 2== | ==Oppgave 2== | ||
[[File:26082022-01.png]] [[File:26082022-02.png]] | |||
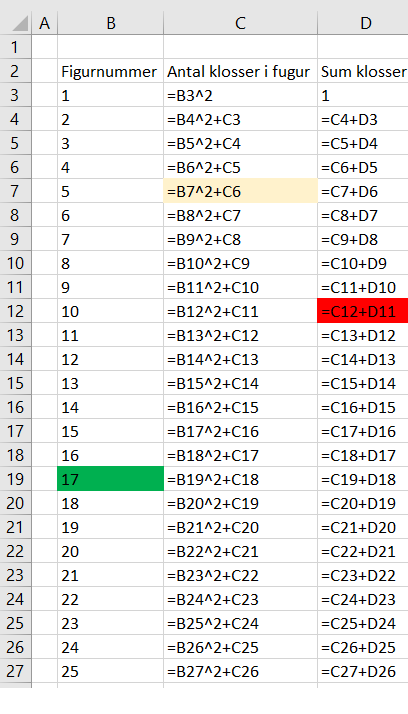
Arket viser figurene fra 1 - 25. Figur nummeret kvadres og figuren før legges til. | |||
===a)=== | |||
55 klosser | |||
===b)=== | |||
1210 klosser | |||
===c)=== | |||
Han kan lage 17 figurer og har 1279 klosser igjen. | |||
==Oppgave 3== | ==Oppgave 3== | ||
[[File:03.09.2022-01.png]] | |||
===a)=== | |||
Se linje 5. | |||
===b)=== | |||
Se linje 8. Må faktorisere ut 3 fra parentesen for å få uttrykket i oppgaven. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
[[File:26082022-03.png]] | |||
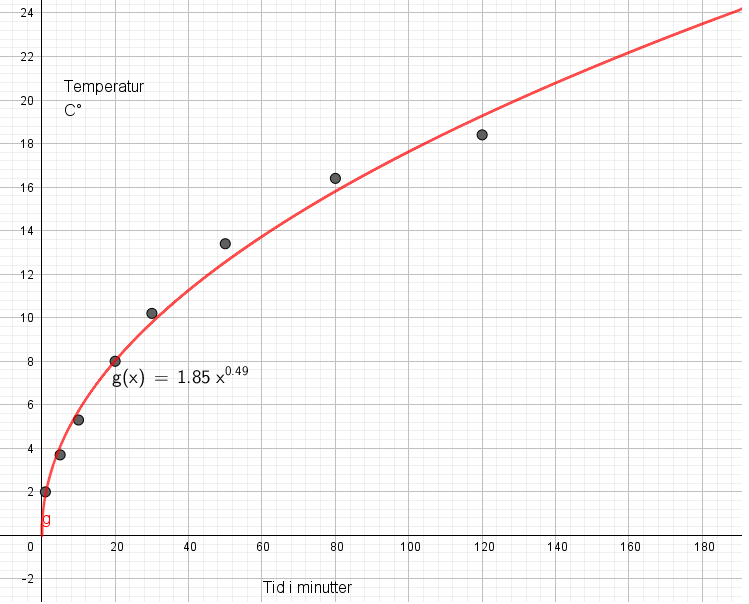
a = 1,85 og b = 0,49. | |||
===b)=== | |||
Modellen overestimerer allerede ved 120 minutter, men man kan si at den gir et greit bilde av temperaturforløpet de to første timene. | |||
===c)=== | |||
Utfører regresjonen i Geogebra og får : $f(x) = -18,09 \cdot 0,98^x$ | |||
===d)=== | |||
[[File:29082022-01.png]] | |||
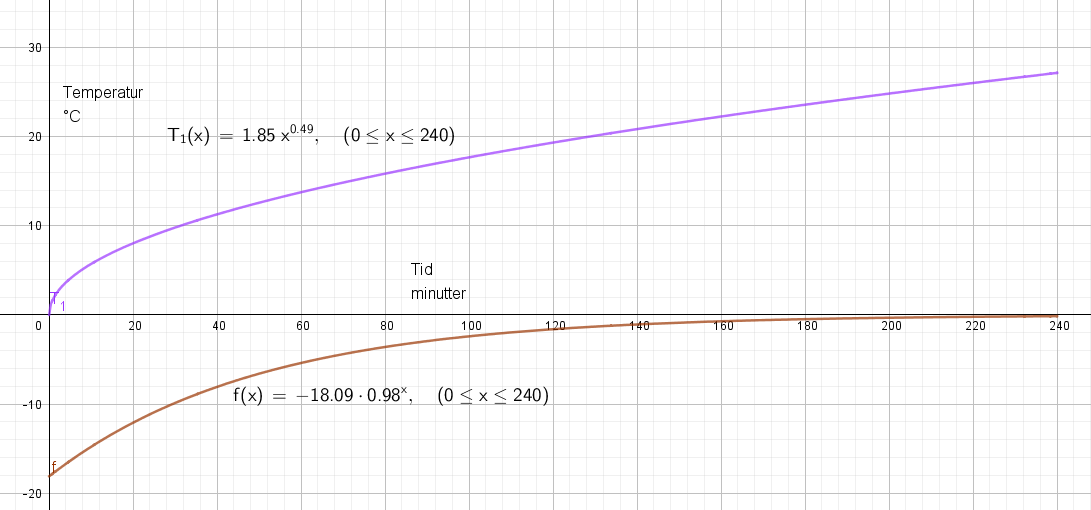
f flater ut og får derved et større gyldighetsområde. T vokser hele tiden og vil avvike fra virkeligheten etter ca 120 minutter. | |||
===e)=== | |||
$T_2(x)= -18,09 \cdot 0,98^x +20 $ | |||
$T_2(240)= -18,09 \cdot 0,98^{240} + 20 = 19,9 $ grader Celsius. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
Funksjonen har et min eller makspunkt i (1, f(1)). Stingningstall 6 for x=4 gir et minimumspunkt i (1,f(1)) | |||
$f(x)=ax^2+bx+c$ | |||
$f'(x) =2ax+b $ | |||
$1 = \frac{-b}{2a}$ og 8a + b = 6 gir f'(x) = 2x-2 | |||
===b)=== | |||
Det betyr at c = 4. a og b har vi fra oppgave a: | |||
$f(x)= x^2-2x+4$ | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
[[File:06092022-01.png]] | |||
Linje 2: x = 0 | |||
===b)=== | |||
'Se linje 3. b = - 3 eller b = 3. | |||
===c)=== | |||
Se linje 5 og 6. | |||
Siste sideversjon per 22. mai 2024 kl. 17:36
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsning del 1 av Lektor Lainz
Videoløsning del 2 av Lektor Lainz
Videoløsn. del 1 av matematikk.net
DEL EN
Oppgave 1
a)
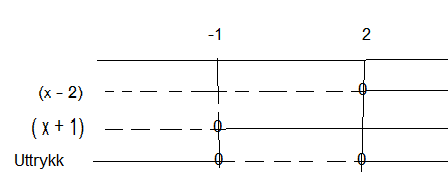
$(x-2)(x+1) =0 $
$ x-2=0 \vee x+1=0 $
$x=2 \vee x=-1$
b)
I området fra -1 til 2 er produktet i a negativt. En mulig ulikhet blir da (x-2)(x-1) > 0. (tegn fortegnsskjema dersom du ikke ser det direkte).
Oppgave 2
$9x^2-30x +r = (3x-s)^2 = 9x^2 - 6sx +s^2 $
Ser at s må være 5 og r lik $s^2. r = 25$
Oppgave 3
Når tangens til en vinkel er $\frac 34$ betyr det at forholdene mellom katene er 3/4. Katetene kan ha lengdene 3 og 4, 6 og 8, osv.
Sinus til vinkel B kan IKKE være 3/10, fordi det er forholdet mellom motstående katet og hypotenus. Dersom katetet er 3 er hypotenusen 5 og dersom hypotenusen er 10 er katetet 6.
Katetetene kan være 6 og 8 fordi forholdet mellom dem da er 3/4.
Hypotenusen kan være kortere enn 4. dersom et katet er 0,75 og det andre er 1,0 er forholdet 3/4 og hypotenusen mindre enn 4.
Oppgave 4
Først defineres en funksjon f som kvadrerer x.
Så løper løkken gjennom tallene 1,2,3 osv. Disse kvadreres og printes. Når verdien til kvadratet når 400 stopper programmet.
Programmet printer ut de 20 første kvadrattallene.
Oppgave 5
Vertikal asymptote er nevnerens nullpunkt. Dersom nevneren er (x+2) gir det vertikal asymptote x = -2. Dersom x går mot uendelig skal f gå mot 3.
$f(x)= \frac{3x}{x+2}$ eller $f(x) = \frac{6x}{2x + 4}$ er eksempler på slike funksjoner.
Oppgave 6
a)
f(3) = 0 derfor er f delelig på (x-3)
b)
$f(0) = -9$, kan derfor utelukke grafen i A.
Dersom vi deriverer funksjonen ser man at x koordinatene til ekstremalpunktene ligger nesten like langt fra origo, på hver sin side av y aksen. Det stemmer med grafen i figur C.
DEL TO
Oppgave 1
Løser oppgaven i Geogebra.
a)
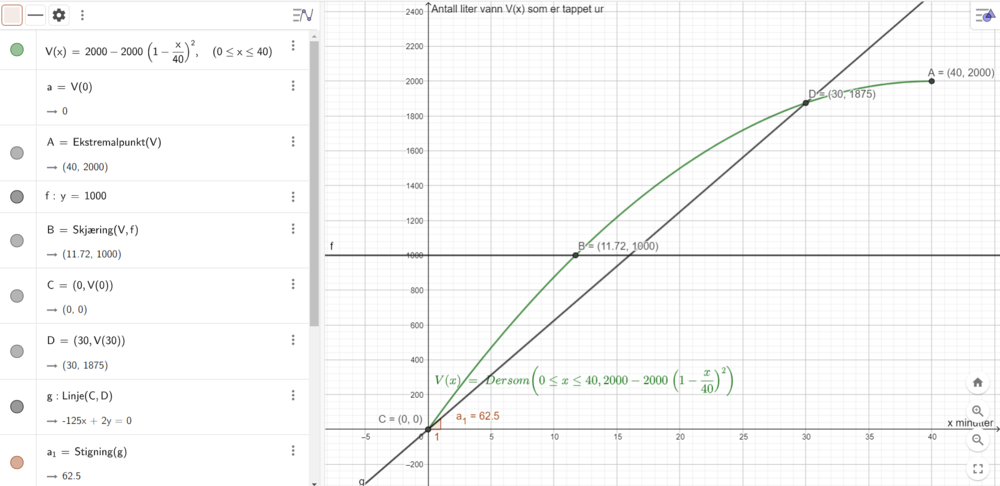
$V(0)=0$ (se algebrafeltet på skjermbildet). Det vil si at før tappingen starter (ved 0 minutter), så har det ikke blitt tappet ut noe vann av tanken (0 liter).
b)
Verdimengden til V er 2000. Jeg fant høyeste punkt på grafen, A=(40,2000), ved å bruke knappen "Ekstremalpunkt". Laveste punkt er (0,0). Verdimengden er da 2000 - 0 = 2000.
c)
Lager linjen y = 1000, og bruker knappen "skjæring mellom to objekt" mellom linjen og grafen til V. Får punkt B=(11.7, 1000). Det vil si at det tar 11,7 minutter før halvparten av vannet er tappet ut av tanken. Se punkt B.
d)
Lager punkt C=(0,V(0)) og D=(30,V(30)), og lager en linje som gå gjennom disse to punktene med knappen "linje". Finner stigningstallet til linjen med knappen "stigning". Stigningstallet er 62,5 (se verdien a1 i algebrafeltet). Svaret forteller oss at fra 0 til 30 minutter etter at tappingen har startet, tappes vannet med en gjennomsnittlig fart på 62,5 liter per minutt.
e)
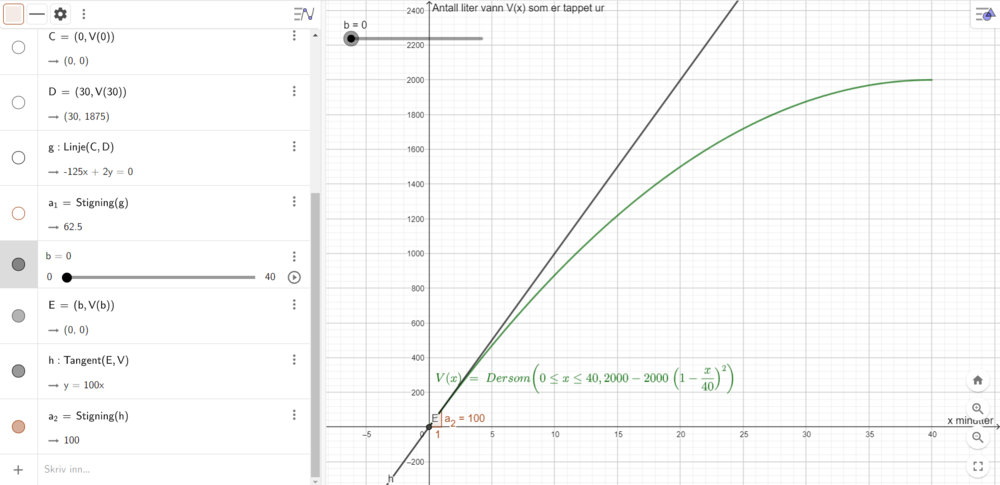
Lager en glider b med kommandoen "glider(0,40,1)". Lager et punkt E=(b,V(b)) og tangenten til V i punktet E med knappen "tangenter". Viser stigningstallet til tangenten med knappen "stigning". Flytter på glideren slik at punkt E flytter seg langs hele grafen til V, og ser om stigningstallet noen gang overstiger 105. Jeg finner at det høyeste stigningstallet er 100, når E=(0,0). Se verdien a2 i algebrafeltet.
Det vil altså aldri tappes mer enn 105 liter i løpet av ett minutt.
Oppgave 2
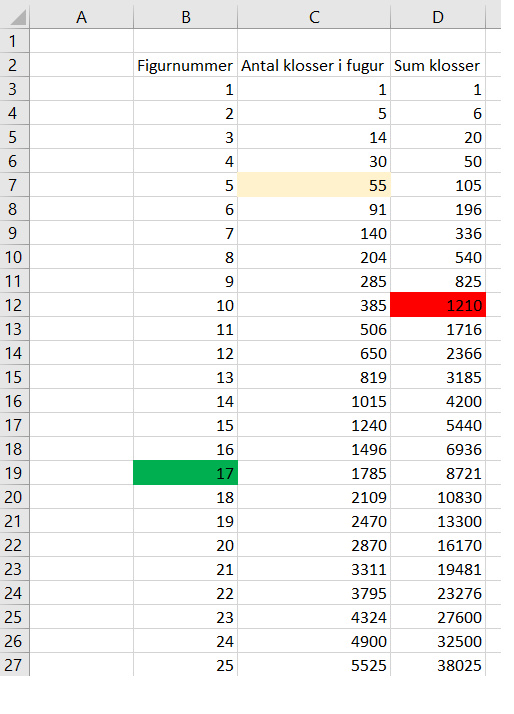
Arket viser figurene fra 1 - 25. Figur nummeret kvadres og figuren før legges til.
a)
55 klosser
b)
1210 klosser
c)
Han kan lage 17 figurer og har 1279 klosser igjen.
Oppgave 3
a)
Se linje 5.
b)
Se linje 8. Må faktorisere ut 3 fra parentesen for å få uttrykket i oppgaven.
Oppgave 4
a)
a = 1,85 og b = 0,49.
b)
Modellen overestimerer allerede ved 120 minutter, men man kan si at den gir et greit bilde av temperaturforløpet de to første timene.
c)
Utfører regresjonen i Geogebra og får : $f(x) = -18,09 \cdot 0,98^x$
d)
f flater ut og får derved et større gyldighetsområde. T vokser hele tiden og vil avvike fra virkeligheten etter ca 120 minutter.
e)
$T_2(x)= -18,09 \cdot 0,98^x +20 $
$T_2(240)= -18,09 \cdot 0,98^{240} + 20 = 19,9 $ grader Celsius.
Oppgave 5
a)
Funksjonen har et min eller makspunkt i (1, f(1)). Stingningstall 6 for x=4 gir et minimumspunkt i (1,f(1))
$f(x)=ax^2+bx+c$
$f'(x) =2ax+b $
$1 = \frac{-b}{2a}$ og 8a + b = 6 gir f'(x) = 2x-2
b)
Det betyr at c = 4. a og b har vi fra oppgave a:
$f(x)= x^2-2x+4$
Oppgave 6
a)
Linje 2: x = 0
b)
'Se linje 3. b = - 3 eller b = 3.
c)
Se linje 5 og 6.