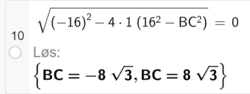1T 2022 høst LK20 LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (18 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 3: | Linje 3: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=54153 Diskusjon av oppgaven på matteprat] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=54153 Diskusjon av oppgaven på matteprat] | ||
[https://www.youtube.com/watch?v=_EFQzWiXPUM Videoløsning av UDL.no] | |||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=54153&p=247720#p247720 Løsningsforslag som pdf laget av Farhan Omar] | |||
[https://youtu.be/XUjHszcqZL0 Videoløsn. del 1 laget av matematikk.net] | |||
[https://www.youtube.com/watch?v=L4_eajjl_10 VIDEO 2.1 laget av matematikk.net] | |||
[https://youtu.be/6oNVx85vUA0 Videoløsning del 1 laget av Lektor Lainz] | |||
==DEL EN== | ==DEL EN== | ||
| Linje 128: | Linje 137: | ||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | |||
$r=2\sqrt{3}$, se CAS linje 1. Bruker arealsetningen. | |||
[[File: 1T-H22-del2-3.png|350px]] | |||
===b)=== | |||
Se bilde av CAS. | |||
Linje 2: finner vinkel B. | |||
Linje 3: bruker sinussetningen til å finne lengden BC. | |||
Linje 4: finner lengden AB, som er det dobbelte av radius. | |||
Linje 5: Bruker arealsetningen til å finne arealet til ABC. | |||
==Oppgave 4 == | ==Oppgave 4 == | ||
===a)=== | |||
$14^2 = 16^2 + x^2 −16x$ | |||
Dette forteller oss at det er en trekant med side $a = 14$, $b = 16$, $c = x$, og at $2bc\cdot cos(A)=16x$, som gir $cos(A)=0.5$ | |||
Det vil si at vinkel A er 60 grader. | |||
===b)=== | |||
Løser likningen i CAS. Får løsningene $x=6$ og $x=10$ | |||
[[File: H22-1T-del2-4.png|300px]] | |||
===c)=== | |||
Jeg vil løse likningen $x^2-16x+16^2-BC^2=0$ slik at den bare har én løsning. Da må diskriminanten i abc-formelen være lik 0. Bruker CAS til å løse dette: | |||
[[File: H22-1T-del2-4b.png|250px]] | |||
$BC=8\sqrt{3}$ gir bare én mulig trekant. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
Bruker regresjonsanalyse i Geogebra. Modellen blir $S(x)=2.03x^{0.47}$ | |||
===b)=== | |||
$\sqrt{9.81}\approx 3,13$ og $\pi\approx 3,14$, så vi kan forkorte pi med roten av g i formelen. Dermed har vi: | |||
$T=2\pi\sqrt{\frac{L}{g}} = 2\pi\frac{\sqrt{L}}{\sqrt{g}}\approx 2\sqrt{L}$ | |||
===c)=== | |||
Vi kaller snorlengden for x og svingetiden for S(x). Da er formelen fra oppgave b) slik: $S(x)=2\sqrt{x}$ | |||
Dette er tilnærmet samme formel som i oppgave a). $\sqrt{x}$ er det samme som $x^{0.5}$, så vi kan skrive formelen fra c) som $S(x)=2x^{0.5}$. Vi ser at dette er veldig likt formelen i oppgave a). | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
[[File:241122-01.png]] | |||
Det ser jo ganske riktig ut...... | |||
===b)=== | |||
I et rektangel er to og to sider like lange (rettvinklet). Dersom vi har 64 meter til rådighet har to av sidene lengden x. Det som er igjen av lengde er da 64 - 2x fordelt på de to andre sidene, En av disse sidene blir da 32-x (har delt på to). | |||
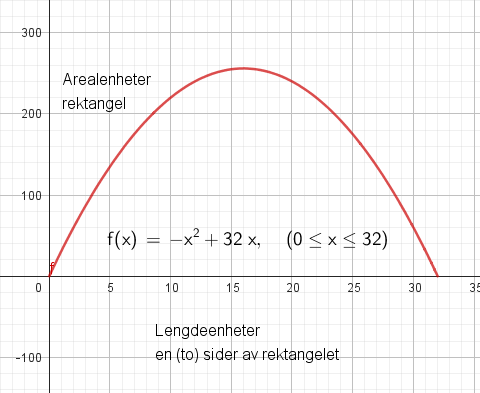
En funksjon for arealet blir da $A(x) = x \cdot (32-x)= -x^2 + 32x$ | |||
[[File:251122-01.png]] | |||
Vi observerer at man får det største arealet ved å lage et kvadrat (sidelengde 16 m), som er et spesialtilfelle av et rektangel. | |||
==Oppgave 7== | ==Oppgave 7== | ||
Løser oppgaven i CAS i Geogebra. | |||
[[File: H22-1T-del2-gardin.png|400px]] | [[File: H22-1T-del2-gardin.png|400px]] | ||
Linje 1-5: finner likning for en av parablene (tenker at origo er i øvre venstre hjørne av parabelen/gardinen). | |||
Linje 6: finner x-verdiene der hvor funksjonsverdien er -35. | |||
Linje 7: legger sammen lengdene til parablene (og kantene) som er langs den stiplede linjen 35 cm fra toppen. | |||
Linje 8: finner omtrentlig verdi. Bedriften må bruke et 468,2 cm langt tøystykke for å lage 8 gardiner. | |||
Siste sideversjon per 22. mai 2024 kl. 17:35
Diskusjon av oppgaven på matteprat
Løsningsforslag som pdf laget av Farhan Omar
Videoløsn. del 1 laget av matematikk.net
VIDEO 2.1 laget av matematikk.net
Videoløsning del 1 laget av Lektor Lainz
DEL EN
Oppgave 1
$tan\,u = \frac{motstående katet}{ hosliggende katet} = \frac 4 3$
$sin\,u = \frac{motstående katet}{ hypotenus} = \frac 4 5$
$cos\,u = \frac{ hosliggende katet}{ hypotenus} = \frac 3 5$
$ \frac{sin\,u}{ cos\,u} = \frac{\frac{4}{5}}{\frac{3}{5}} =\frac{4}{5}\cdot\frac{5}{3} = \frac{4}{3} = tan\,u $
hvilket skulle vises.
Oppgave 2
a)
Nullpunktene til f(x) er x=-4, x=2 og x=4.
Disse nullpunktene passer best med graf A.
b)
Dette er samme uttrykk som f(x) i oppgave a). Vi ser av tegninga til graf A, at f(x)>0 i intervallene $x \in \langle -4,2 \rangle$ og $x \in \langle 4,\rightarrow \rangle$
Oppgave 3
a)
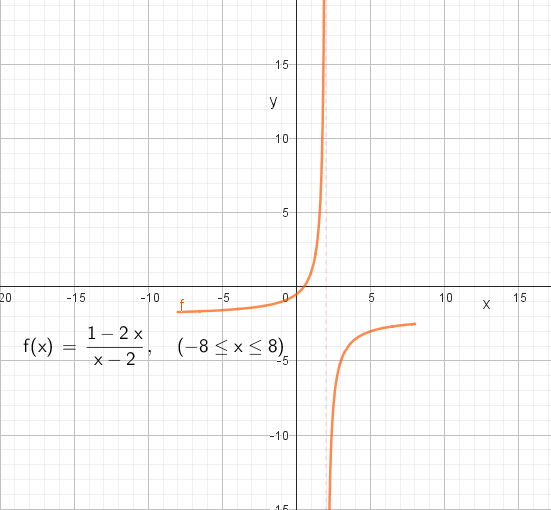
Lars ønsker å bruke programmet til å skrive ut x verdier med tilhørende funksjonsverdi, fra x=8 til x=-8. Det går bra helt til x=2, da prøver programmet å dele på null, og gir feilmelding.
b)
Lars kan legge til en if-setning inni while-løkka, som dersom x=2, skriver ut at funksjonsverdien ikke er definert. For eksempel fra linje 7, inni while-løkka:
if x == 2:
$\quad$ print(x, "funksjonsverdien er ikke definert")
else:
$\quad$ print(x,f(x))
x=x-1
c)
Bruk en verditabell til å tegne punktene inn i et koordinatsystem (for hånd). Grafen til funksjonen skal se slik ut:
Oppgave 4
Den deriverte til en parabel vil være en rett linje.
$f'(-2)= 9$ og $f'(8) =-11$, Dette er punkter på grafen til den deriverte.
Vi er på jakt etter likningen y = ax + b og finner først a:
$a= \frac{\Delta y}{\Delta x} = \frac{y_2 -y_1}{x_2 - x_1} = \frac{-11-9}{8 - (-2)} = -2$
$y = -2x + b$
Så kan vi bruke punktet( 8, -11) og får
$-11 = -2 \cdot 8 + b$ gir b = 5
Desom vi bruker det andre punktet: $9 = -2 \cdot (-2) +b$ gir også b = 5.
Likningen til den deriverte blir y = -2x + 5
DEL TO
Oppgave 1
Oppgaven kan løses grafisk, eller i CAS. Her vist i CAS. Se løsningen til 1P H22 for grafisk løsning.
a)
Da er x null, så temperaturen blir da 3,5 + 34,5 = 38 grader celsius når strømmen slåes av.
Se linje 2 i CAS, T(0) er lik 38.
b)
Se linje 3 i CAS. Det vil ta ca. 5,3 timer før temperaturen er under 20 grader.
c)
Se linje 4 i CAS. Stigningstallet er ca. -3.68 grader per time, mellom 0 og 4 timer etter at strømmen blir slått av. Det vil si at temperaturen gjennomsnittlig synker med 3,68 grader per time i dette intervallet.
d)
Se linje 5 og 6 i CAS. Temperaturen synker ikke med mer enn 5 grader per time, etter at strømmen har blitt slått av. (Modellen T(x) gjelder kun for $x\geq 0$)
Den mest ekstreme momentane endringen er i starten, rett etter at strømmen blir slått av. Da er endringen - 4,8
e)
3,5 er temperaturen til omgivelsene.
Oppgave 2
Antalls treroms er x og antall toroms er y.
x + y = 40
3x+ 2y = 90
Multipliserer første likning med -2. Legger så sammen likningene og får
x = 10. Da er y= 30.
Det er altså 10 treroms og 30 toroms i bygården.
Alternativt kan du tenke at det er 40 leiligheter, og hvis alle var toroms, ville det vært 80 rom til sammen. Siden det er 90 rom til sammen, vet vi da at det er 10 treromsleiligheter. De andre 30 er toromsleiligheter.
Oppgave 3
a)
$r=2\sqrt{3}$, se CAS linje 1. Bruker arealsetningen.
b)
Se bilde av CAS.
Linje 2: finner vinkel B.
Linje 3: bruker sinussetningen til å finne lengden BC.
Linje 4: finner lengden AB, som er det dobbelte av radius.
Linje 5: Bruker arealsetningen til å finne arealet til ABC.
Oppgave 4
a)
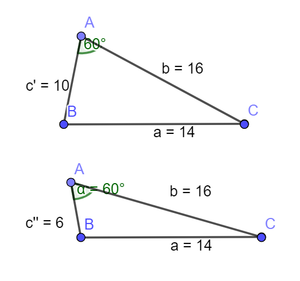
$14^2 = 16^2 + x^2 −16x$
Dette forteller oss at det er en trekant med side $a = 14$, $b = 16$, $c = x$, og at $2bc\cdot cos(A)=16x$, som gir $cos(A)=0.5$
Det vil si at vinkel A er 60 grader.
b)
Løser likningen i CAS. Får løsningene $x=6$ og $x=10$
c)
Jeg vil løse likningen $x^2-16x+16^2-BC^2=0$ slik at den bare har én løsning. Da må diskriminanten i abc-formelen være lik 0. Bruker CAS til å løse dette:
$BC=8\sqrt{3}$ gir bare én mulig trekant.
Oppgave 5
a)
Bruker regresjonsanalyse i Geogebra. Modellen blir $S(x)=2.03x^{0.47}$
b)
$\sqrt{9.81}\approx 3,13$ og $\pi\approx 3,14$, så vi kan forkorte pi med roten av g i formelen. Dermed har vi:
$T=2\pi\sqrt{\frac{L}{g}} = 2\pi\frac{\sqrt{L}}{\sqrt{g}}\approx 2\sqrt{L}$
c)
Vi kaller snorlengden for x og svingetiden for S(x). Da er formelen fra oppgave b) slik: $S(x)=2\sqrt{x}$
Dette er tilnærmet samme formel som i oppgave a). $\sqrt{x}$ er det samme som $x^{0.5}$, så vi kan skrive formelen fra c) som $S(x)=2x^{0.5}$. Vi ser at dette er veldig likt formelen i oppgave a).
Oppgave 6
a)
Det ser jo ganske riktig ut......
b)
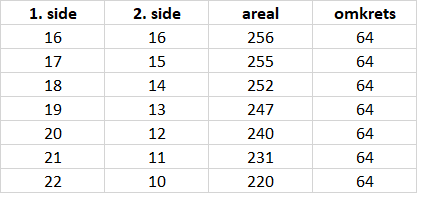
I et rektangel er to og to sider like lange (rettvinklet). Dersom vi har 64 meter til rådighet har to av sidene lengden x. Det som er igjen av lengde er da 64 - 2x fordelt på de to andre sidene, En av disse sidene blir da 32-x (har delt på to).
En funksjon for arealet blir da $A(x) = x \cdot (32-x)= -x^2 + 32x$
Vi observerer at man får det største arealet ved å lage et kvadrat (sidelengde 16 m), som er et spesialtilfelle av et rektangel.
Oppgave 7
Løser oppgaven i CAS i Geogebra.
Linje 1-5: finner likning for en av parablene (tenker at origo er i øvre venstre hjørne av parabelen/gardinen).
Linje 6: finner x-verdiene der hvor funksjonsverdien er -35.
Linje 7: legger sammen lengdene til parablene (og kantene) som er langs den stiplede linjen 35 cm fra toppen.
Linje 8: finner omtrentlig verdi. Bedriften må bruke et 468,2 cm langt tøystykke for å lage 8 gardiner.