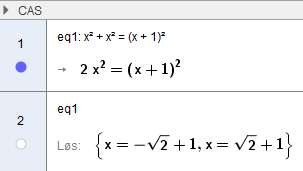1T 2021 Høst eksempel LK20 LØSNING: Forskjell mellom sideversjoner
| (17 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 16: | Linje 16: | ||
===Oppgave 3=== | ===Oppgave 3=== | ||
=== | $x^2 - 4< 2x-1$ | ||
$x^2-2x-3 < 0 $ | |||
$(x - 3)(x + 1 ) <0$ | |||
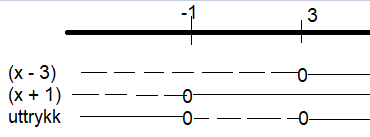
Lager et fortegnsskjema: | |||
[[File:141121-01.png]] | |||
Vi ser at ulikheten er mindre enn null i området -1 til 3. | |||
$x \in <-3, 3>$ | |||
===Oppgave 4=== | |||
Vi tester verdier for x og ser at x = 1 gir en løsning av likningen. Uttrykket er derfor delelig på (x-1) vi utfører polynomdivisjonen | Vi tester verdier for x og ser at x = 1 gir en løsning av likningen. Uttrykket er derfor delelig på (x-1) vi utfører polynomdivisjonen | ||
| Linje 42: | Linje 56: | ||
===Oppgave 6=== | ===Oppgave 6=== | ||
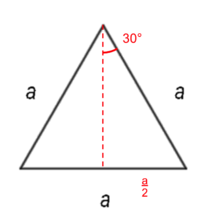
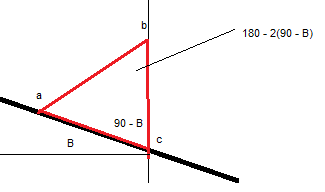
Vi nedfeller høyden i trekanten og får to rettvinklede trekanter. | Vi nedfeller høyden i trekanten og får to rettvinklede trekanter. | ||
Vinkelen mellom høyden og hypotenusen blir 30°: | |||
[[Fil: 1T Eksempel H21 del 1 6.png|200px]] | |||
Siden $\sin(v)=\frac{\text{motstående katet}}{\text{hypotenus}}$ | |||
$\sin(30°)=\frac{\frac{a}{2}}{a}=\underline{\underline{\frac{1}{2}}}$ | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
| Linje 74: | Linje 91: | ||
===Opppgave 3=== | ===Opppgave 3=== | ||
[[File: 141121-02.png]] | |||
===Oppgave 4=== | ===Oppgave 4=== | ||
[[ File: | [[ File:151121-01.png]] | ||
===Oppgave 5=== | |||
===a)=== | |||
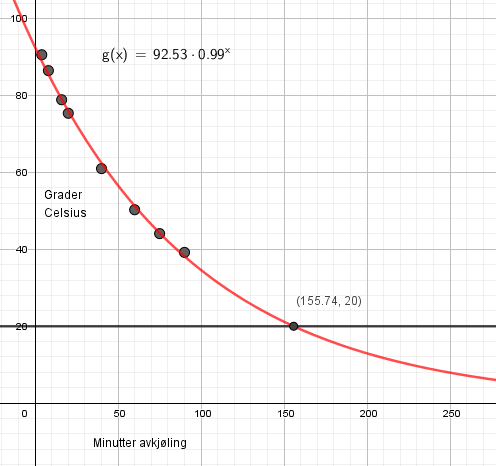
Tallene i tabell en gir oss temperaturen i gelene i avkjølingsforløpet fra 4 minutter til 90 minutter inn i avkjølingen. I dette tidsintervallet er modellen god fordi den følger de faktiske målepunkter godt, $R^2= 0,997 $. Uansett hvor lenge den avkjøles vil den aldri bli kaldere enn romtemperatur, 20 grader celsius. | |||
[[File:061121-04.png]] | |||
Modellen over er god i området 4 - 90 minutter. Vi ser fra de siste målingene at avkjølingen (60, 75, 90) begynner å gå saktere enn hva modellen predikerer. Etter som tiden går vil modellen underestimere temperaturen og etter ca. 156 minutter gir modellen oss verdier under romtemperatur, noe som ikke er i samsvar med virkeligheten. | |||
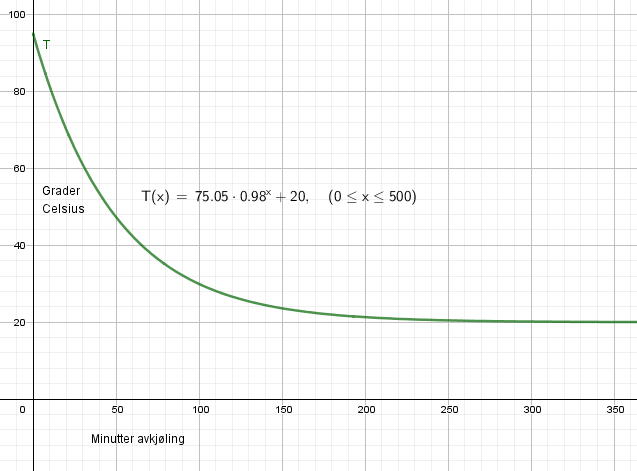
Vi trenger en modell som nærmere seg romtemperatur når tiden blir stor. Stine trekker fra 20 grader på alle målingen. Kjører man regresjon på tabell to i oppgaven får man et utrykk som dette $f(x)=75,05 \cdot 0,98^x$. Dersom vi plusser på romtemperaturen får vi | |||
[[File:081121-04.png]] | |||
===b)=== | |||
Modellen er gyldig så lenge romtemperaturen er stabil. | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
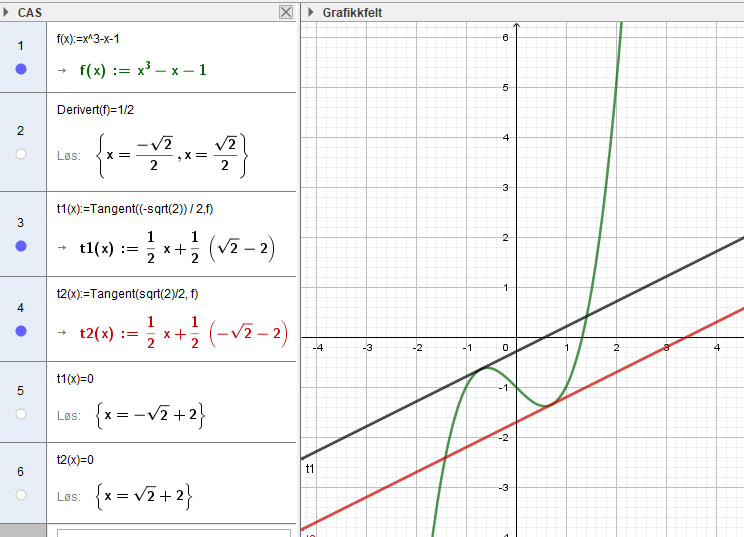
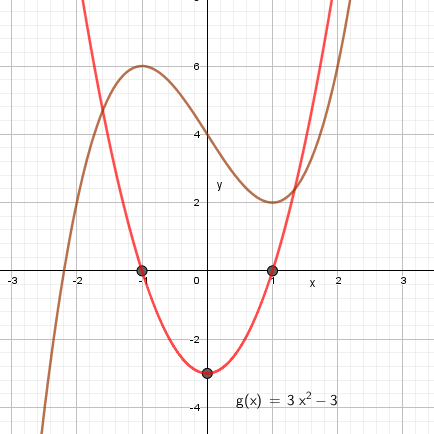
Grafen til den deriverte har nullpunkter i -1, 0 og i 1, 0 . Den har et minimum i (0 , -3). det ser vi fra stigningstallet til vendetangenten. Vi setter disse inn i Geogebra og kjører polynomregresjon. | |||
[[File: 081121-05.png]] | |||
Utrykket til den deriverte av f er $ 3x^2-3$ | |||
===Oppgave 7=== | ===Oppgave 7=== | ||
===a)=== | |||
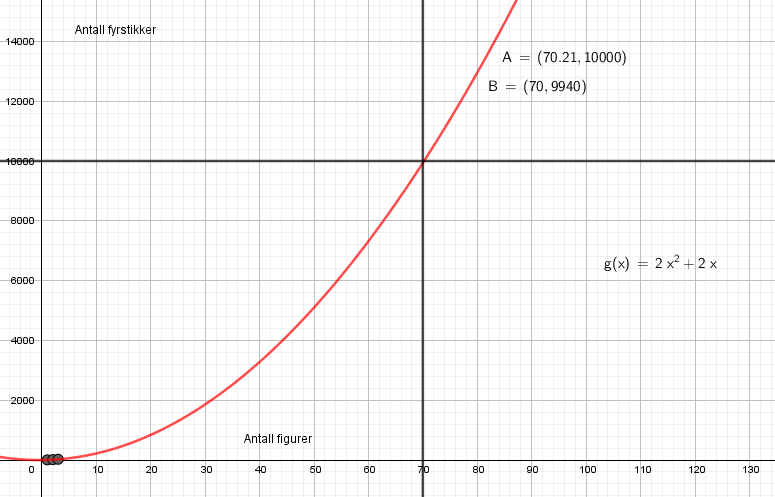
[[File:061121-01.png]] | |||
Bruker regresjon, finner et funksjonsuttrykk og ser at man kan lage 70 figurer. | |||
===b)=== | |||
Man får 60 fyrstikker tilovers. | |||
==Oppgave 8== | |||
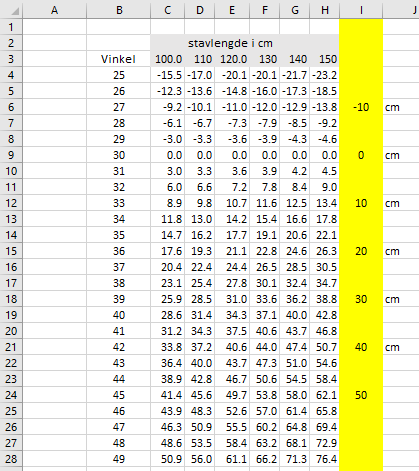
[[File:31122021-01.png]] | |||
Terrengets vinkel er gitt i kolonne B. Den gule kolonnen I gir oss resultatene fra "Stavmetoden". Selve tabellen gir oss fasit i forhold til underlagsvinkel og stavlengde. V ser at modellen passer god når underlagsvinkelen er i nærheten av 30 grader og stavlengden er 110 - 120 cm. | |||
Tabellen baserer seg på kosinussetningen: | |||
[[File:31122021-02.png]] | |||
Siste sideversjon per 25. mar. 2024 kl. 10:07
DEL EN
Oppgave 1
a)
Stigningstall : $a = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2- x_1} = \frac{7,3 - 4,7}{14 - 4} = \frac {2,6}{10} = 0,26$
b)
Temperaturen øker i gjennomsnitt med 0,26 grader i timen, fra 04 om natten, til 2 om ettermiddagen.
Oppgave 2
Siden AC er den lengste siden i den rettvinklede trekanten er AC hypotenusen. Tangens til en vinkel er motstående katet delt på hossliggende katet. For at det forholdet skal bi 1 må BC = AB = 4.
Oppgave 3
$x^2 - 4< 2x-1$
$x^2-2x-3 < 0 $
$(x - 3)(x + 1 ) <0$
Lager et fortegnsskjema:
Vi ser at ulikheten er mindre enn null i området -1 til 3.
$x \in <-3, 3>$
Oppgave 4
Vi tester verdier for x og ser at x = 1 gir en løsning av likningen. Uttrykket er derfor delelig på (x-1) vi utfører polynomdivisjonen
$x^3- 3x^2 -x + 3 : (x-1)$ og får som svar $x^2-2x -3$ som faktorisert er (x +1)(x-3). Bruk abc formelen om du ikke "ser" det.
Vi står da med følgende: (x-1)(x+1)(x-3)=0
Det gir løsninger for $x \in \{ -1, 1, 3 \}$
Oppgave 5
a)
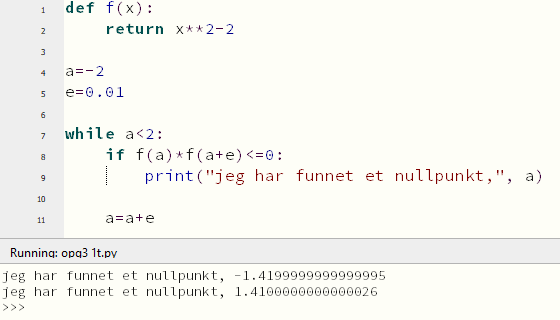
Linje 8: print("Diskriminant er negativ, ingen reelle løsninger")
Linje 10: print("Diskriminant lik null, en dobbeltrot")
Linje 12: print("Denne likningen har to løsninger")
b)
Programmet regner ut $d=b^2 -4ac$ til å være lik null, altså en dobbeltrot.
Oppgave 6
Vi nedfeller høyden i trekanten og får to rettvinklede trekanter. Vinkelen mellom høyden og hypotenusen blir 30°:
Siden $\sin(v)=\frac{\text{motstående katet}}{\text{hypotenus}}$
$\sin(30°)=\frac{\frac{a}{2}}{a}=\underline{\underline{\frac{1}{2}}}$
Oppgave 7
a)
f(0) = 3, f(-1) = 0 og f(-3) = 0. Det er altså grafen til f som er tegnet.
b)
Parabelen flyttes, men "smilet" er det samme, hvilket bety at koeffisienten a fortsatt er lik 1. Symmetrilinje $x = \frac{-b}{2a}$. Siden x = - 4 og a =1 må b = 8.
Vi vet at g(-4) = 1, det gir c = 17. Altså får vi $g(x) = x^2 + 8x +17$
DEL TO
Oppgave 1
r, s og t skal ha verdier som gjelder for alle verdier av x. Vi skriver $(sx + t)^2 = (sx + t)(sx + t)$ og ser at s = 2 fordi koefisienten i andregradsleddet er 4. t = 4 fordi t skal multipliseres med 2 og vi har to slike ledd. Til slutt blir r = 16 fordi $t^2 = r = 16$.
Oppgave 2
Lengden av sidene i kvadratet er $1 + \sqrt 2$.
Opppgave 3
Oppgave 4
Oppgave 5
a)
Tallene i tabell en gir oss temperaturen i gelene i avkjølingsforløpet fra 4 minutter til 90 minutter inn i avkjølingen. I dette tidsintervallet er modellen god fordi den følger de faktiske målepunkter godt, $R^2= 0,997 $. Uansett hvor lenge den avkjøles vil den aldri bli kaldere enn romtemperatur, 20 grader celsius.
Modellen over er god i området 4 - 90 minutter. Vi ser fra de siste målingene at avkjølingen (60, 75, 90) begynner å gå saktere enn hva modellen predikerer. Etter som tiden går vil modellen underestimere temperaturen og etter ca. 156 minutter gir modellen oss verdier under romtemperatur, noe som ikke er i samsvar med virkeligheten.
Vi trenger en modell som nærmere seg romtemperatur når tiden blir stor. Stine trekker fra 20 grader på alle målingen. Kjører man regresjon på tabell to i oppgaven får man et utrykk som dette $f(x)=75,05 \cdot 0,98^x$. Dersom vi plusser på romtemperaturen får vi
b)
Modellen er gyldig så lenge romtemperaturen er stabil.
Oppgave 6
Grafen til den deriverte har nullpunkter i -1, 0 og i 1, 0 . Den har et minimum i (0 , -3). det ser vi fra stigningstallet til vendetangenten. Vi setter disse inn i Geogebra og kjører polynomregresjon.
Utrykket til den deriverte av f er $ 3x^2-3$
Oppgave 7
a)
Bruker regresjon, finner et funksjonsuttrykk og ser at man kan lage 70 figurer.
b)
Man får 60 fyrstikker tilovers.
Oppgave 8
Terrengets vinkel er gitt i kolonne B. Den gule kolonnen I gir oss resultatene fra "Stavmetoden". Selve tabellen gir oss fasit i forhold til underlagsvinkel og stavlengde. V ser at modellen passer god når underlagsvinkelen er i nærheten av 30 grader og stavlengden er 110 - 120 cm.
Tabellen baserer seg på kosinussetningen: