Trigonometriske likninger: Forskjell mellom sideversjoner
| (53 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
Det finnes forskjellige typer trigonometriske | Det finnes forskjellige typer trigonometriske likninger og ofte er det forskjellige måter å løse dem på. Nedenfor følger en oversikt over de vanligste typene og et forslag til hvordan de kan løses. | ||
Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende: | Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende: | ||
| Linje 9: | Linje 9: | ||
:<math>\tan(x+\pi)=\tan\,x</math> | :<math>\tan(x+\pi)=\tan\,x</math> | ||
===Trigonometriske | ===1. Trigonometriske grunnlikninger=== | ||
Trigonometriske | Trigonometriske likninger som kun involverer én trigonometrisk funksjon, kaller vi trigonometriske grunnlikninger. Disse er de enkleste trigonometriske likningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser. | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Løsningsmetode for trigonometriske grunnlikninger''' | |||
Vi tar for oss ligningen | |||
$a\sin(bx)=c$ | |||
Vi vil løse denne ligninger for <math>x</math>. Det første vi gjør er å isolere <math>\sin(bx)</math> på venstresiden: | |||
$\sin(bx)=\frac ca$ | |||
Siden høyresiden er lik venstresiden, vil <math>\arcsin</math> av høyresiden være lik <math>\arcsin</math> av venstresiden. Altså: | |||
$\arcsin(\sin(bx))=\arcsin(\frac ca)$ | |||
Dette gir oss to uttrykk for <math>x</math>: | |||
$bx=\arcsin(\frac ca)\,\vee\,\pi-bx=\arcsin(\frac ca)$ | |||
Sinus er periodisk i <math>2\pi</math> så vi må legge til en vilkårlig multippel av <math>2\pi</math> på hver side. | |||
<math>bx+k\cdot2\pi=\arcsin(\frac ca)\,\vee\,\pi-bx+k\cdot2\pi=\arcsin(\frac ca)\,,\,k\in\mathbb{Z}</math> | |||
:Når vi isolerer <math>x</math> på venstresiden får vi | :Når vi isolerer <math>x</math> på venstresiden får vi | ||
::<math>x=\frac{\arcsin(\frac ca)-k\cdot2\pi}{b}\,\vee\,x=\frac{\arcsin(\frac ca)-\pi(2k+1)}{b}\,,\,k\in\mathbb{Z}</math> | ::<math>x=\frac{\arcsin(\frac ca)-k\cdot2\pi}{b}\,\vee\,x=\frac{\arcsin(\frac ca)-\pi(2k+1)}{b}\,,\,k\in\mathbb{Z}</math> | ||
Den samme fremgangsmåten kan benyttes på trigonometriske | Den samme fremgangsmåten kan benyttes på trigonometriske grunnlikninger med <math>\cos</math> og <math>\tan</math> også, men husk at disse har litt forskjellige egenskaper, så løsningene blir ikke de samme. | ||
</div> | </div> | ||
==='''EKSEMPEL 1.'''=== | |||
==='''EKSEMPEL'''=== | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''COS''' | '''COS''' | ||
$2cos(\pi x)=1 \quad \quad \quad x\in [0, 2\pi> | $2cos(\pi x)=1 \quad \quad \quad x\in [0, 2\pi> $ | ||
$cos( \pi x) = \frac 12 \\ \pi x = \frac{\pi}{3} +k2\pi \vee \pi x $ | |||
$= 2\pi-\frac{\pi}{3} + k2\pi \\ x= \frac 13+2k \vee x=2- \frac13 +2k \\ x= \frac 13 \vee x= \frac 73 \vee x= \frac{13}{3} \vee x= \frac 53 \vee x= \frac{11}{3} \vee x= \frac{17}{3}$ | |||
$x \in${$ \frac{1}{3}, \frac{5}{3}, \frac{7}{3}, \frac{11}{3}, \frac{13}{3}, \frac{17}{3}$} | $x \in${$ \frac{1}{3}, \frac{5}{3}, \frac{7}{3}, \frac{11}{3}, \frac{13}{3}, \frac{17}{3}$} | ||
| Linje 74: | Linje 85: | ||
</div> | </div> | ||
=== | ===2)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 83: | Linje 94: | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 2.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| Linje 95: | Linje 106: | ||
Merk at <math>\frac{\sqrt{5}+1}{2}>1</math>, altså har ikke denne | Merk at <math>\frac{\sqrt{5}+1}{2}>1</math>, altså har ikke denne grunnlikningen noen løsninger. | ||
Vi står igjen med kun den første trigonometriske | Vi står igjen med kun den første trigonometriske grunnlikningen. Når vi løser denne, får vi | ||
$x= 0,67 \vee x= 2,48$ | $x= 0,67 \vee x= 2,48$ | ||
| Linje 109: | Linje 120: | ||
</div> | </div> | ||
=== | ===3)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 118: | Linje 129: | ||
</div> | </div> | ||
===Eksempel 3.=== | |||
===Eksempel | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| Linje 131: | Linje 141: | ||
</div> | </div> | ||
=== | ===4)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 137: | Linje 147: | ||
$a cos^2 x + b sin x + c = 0 \quad$ eller $ \quad a sin^2 x + b cos x + c = 0$<p></p> | $a cos^2 x + b sin x + c = 0 \quad$ eller $ \quad a sin^2 x + b cos x + c = 0$<p></p> | ||
Ligningen løses ved å erstatte $ | Ligningen løses ved å erstatte $sin^2x \quad $ med $1 - cos^2 x \quad$ eller $ cos^2 x \quad$ med $1 - sin^2 x$ | ||
</div> | </div> | ||
==='''Eksempel | ==='''Eksempel 4.'''=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
:::<math>\sin\,x+2cos^2x=1\,,\,x\in[0,2\pi > </math> | :::<math>\sin\,x+2cos^2x=1\,,\,x\in[0,2\pi > </math> | ||
::Vi kjenner identiteten <math>\sin^2x+\cos^2x=1</math>. Den kan vi bruke her for å omforme ligningen til | ::Vi kjenner identiteten <math>\sin^2x+\cos^2x=1</math>. | ||
Den kan vi bruke her for å omforme ligningen til | |||
:::<math>\sin\,x+2-2\sin^2x=1</math> | :::<math>\sin\,x+2-2\sin^2x=1</math> | ||
| Linje 152: | Linje 164: | ||
:::<math>2\sin^2x-\sin\,x-1=0</math> | :::<math>2\sin^2x-\sin\,x-1=0</math> | ||
::Dette er en andregradslikning i | ::Dette er en andregradslikning i $\sin\,x$, som vi kan løse: | ||
:::<math>\sin\,x=\frac{1\pm\sqrt{1+8}}{4}=\frac{1\pm 3}{4}</math> | :::<math>\sin\,x=\frac{1\pm\sqrt{1+8}}{4}=\frac{1\pm 3}{4}</math> | ||
| Linje 164: | Linje 176: | ||
$x= \frac {\pi}{2} \vee x= \frac{7 \pi}{6} \vee x= \frac{11 \pi}{6}$ | $x= \frac {\pi}{2} \vee x= \frac{7 \pi}{6} \vee x= \frac{11 \pi}{6}$ | ||
$x \in${$\frac {\pi}{2}, \frac{7 \pi}{6}, \frac{11 \pi}{6}$} | |||
Slik ser det ut: | Slik ser det ut: | ||
| Linje 170: | Linje 184: | ||
</div> | </div> | ||
=== | ===5)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
<math>a sin^2 x + b sin x cos x + c cos^2 x = 0</math><p></p> | <math>a sin^2 x + b sin x cos x + c cos^2 x = 0</math><p></p> | ||
Løses ved å dividere begge sider av likhetstegnet med $cos^2 x$ | Løses ved å dividere begge sider av likhetstegnet med $cos^2 x \quad \quad cos x \neq 0$ | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 5.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
$2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi>\\ 2tan^2x+3tanx-1=0 \\ 2u^2+3u | $2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi>\\ 2tan^2x+3tanx-1=0 \\ 2u^2+3u-1=0$ | ||
$tan x =-1,06 \vee tanx = 0,27 \\x= -1,06 + k\pi \vee x= 0,27 + k\pi \\ x = 0,27 \vee x=3,45 \vee x=2,08 \vee x=5,22 $ | |||
$x \in$ {0,27 , 2,08 , 3,45 , 5,22} | |||
Slik ser det ut: | Slik ser det ut: | ||
| Linje 192: | Linje 207: | ||
</div> | </div> | ||
=== | ===6)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 199: | Linje 214: | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 6. === | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
[[Bilde:Trig-3-4-3- | $4sin^2x+ sinx cos x - 3cos^2x=3 \quad \quad x \in [0, 2\pi> \\4sin^2x+ sinx cos x - 3cos^2x = 3sin^2x + 3cos^2x \\ sin^2x + sinx cosx - 6cos^2 =0 \\ tan^2x + tanx - 6 = 0 \\ tanx = -3 \vee tanx = 2 \\ x= -1,24 +k\pi \vee x=1,11 + k\pi \\ x= 1,11 \vee x= 4,25 \vee x= 1,90 \vee x=5,04 $ | ||
$x \in ${1,11 , 1,90 , 4,25 , 5,04} | |||
Slik ser det ut: | |||
[[Bilde:Trig-3-4-3-14.png]] | |||
</div> | </div> | ||
=== | ===7)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;">Likninger av typen<p></p> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;">Likninger av typen<p></p> | ||
:::<math>a\sin cx + bcos cx = d</math> <p></p> | :::<math>a\sin cx + bcos cx = d</math> <p></p> | ||
Løses ved å skrive om til: <p></p> | Løses ved å skrive om til: <p></p> | ||
:::<math> Asin (cx + \varphi)=d</math> der <math>A=\sqrt{a^2+b^2}</math> og <math>\varphi</math> er gitt ved<math>\varphi = \frac ba</math> og <math>\varphi</math>ligger i samme kvadrant som (a,b). | :::<math> Asin (cx + \varphi)=d</math> der <math>A=\sqrt{a^2+b^2}</math> og <math>\varphi</math> er gitt ved <math> tan \varphi = \frac ba</math> og <math>\varphi</math>ligger i samme kvadrant som (a,b). | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 7.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
:'''Eksempel:'''<p></p> | :'''Eksempel:'''<p></p> | ||
<math>sin x + cos x = 1</math> <p></p> | <math>sin x + cos x = 1 \quad \quad \quad x\in [0,2\pi></math> <p></p> | ||
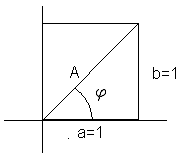
<math> A=\sqrt{a^2+b^2}= \sqrt 2 \\ a = b = 1 </math><p></p> | <math> A=\sqrt{a^2+b^2}= \sqrt 2 \\ a = b = 1 </math><p></p> | ||
Vinkelen <math>\varphi</math> ligger i første kvadrant, <math>\varphi =tan^{-1}(1)= \frac {\pi}{4} </math> | Vinkelen <math>\varphi</math> ligger i første kvadrant, <math>\varphi =tan^{-1}(1)= \frac {\pi}{4} </math> | ||
| Linje 229: | Linje 249: | ||
<p></p>Vi får<p></p> | <p></p>Vi får<p></p> | ||
$\sqrt 2 sin(x + \frac \pi 4) = 1 \\ sin (x+ \frac \pi 4) = \frac{\sqrt 2}{2} \\ x + \frac {\pi}{4} = \frac {\pi}{4} +2k\pi \vee x + \frac{\pi}{4}= \pi - \frac{\pi}{4} +2k\pi \\ x=0 \vee x= \frac {\pi}{2}$ | |||
$x \in$ {0, $\frac \pi 2$} | |||
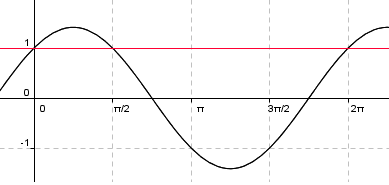
Det ser slik ut: | |||
[[Bilde:sincos.png]] | [[Bilde:sincos.png]] | ||
| Linje 235: | Linje 260: | ||
</div> | </div> | ||
===8)=== | |||
=== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 245: | Linje 269: | ||
</div> | </div> | ||
=== Eksempel | === Eksempel 8.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske | Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnlikninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen | ||
<math>\sin\,x\,\cos\,x-cos\,x=0\,,\,x\in [0,2\pi></math> | <math>\sin\,x\,\cos\,x-cos\,x=0\,,\,x\in [0,2\pi></math> | ||
Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på <math>\cos\,x</math>. | Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på <math>\cos\,x</math>. Generelt prøver man å ikke dele eller multiplisere med funksjoner av variabler, fordi du kan miste løsninger, eller lage falske løsninger. Dette gjelder generelt når du deler på null eller multipliserer med null. I stedet faktoriserer vi ligningen: | ||
<math>\cos\,x\,(\sin\,x-1)=0</math> | <math>\cos\,x\,(\sin\,x-1)=0</math> | ||
:Nå ser vi at for at ligningen skal oppfylles, må <math>\cos\,x=0</math> eller <math>\sin\,x-1=0</math>. Vi har klart å redusere den kompositte trigonometriske ligningen til to trigonometriske | :Nå ser vi at for at ligningen skal oppfylles, må <math>\cos\,x=0</math> eller <math>\sin\,x-1=0</math>. Vi har klart å redusere den kompositte trigonometriske ligningen til to trigonometriske grunnlikninger. | ||
::<math>\sin\,x=1 \,\Rightarrow\, x=\frac{\pi}{2}</math> | ::<math>\sin\,x=1 \,\Rightarrow\, x=\frac{\pi}{2}</math> | ||
Siste sideversjon per 8. aug. 2023 kl. 03:33
Det finnes forskjellige typer trigonometriske likninger og ofte er det forskjellige måter å løse dem på. Nedenfor følger en oversikt over de vanligste typene og et forslag til hvordan de kan løses.
Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende:
- <math>\sin(x+2\pi)=\sin\,x</math>
- <math>\cos(x+2\pi)=\cos\,x</math>
- <math>\tan(x+\pi)=\tan\,x</math>
1. Trigonometriske grunnlikninger
Trigonometriske likninger som kun involverer én trigonometrisk funksjon, kaller vi trigonometriske grunnlikninger. Disse er de enkleste trigonometriske likningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser.
Løsningsmetode for trigonometriske grunnlikninger
Vi tar for oss ligningen
$a\sin(bx)=c$
Vi vil løse denne ligninger for <math>x</math>. Det første vi gjør er å isolere <math>\sin(bx)</math> på venstresiden:
$\sin(bx)=\frac ca$
Siden høyresiden er lik venstresiden, vil <math>\arcsin</math> av høyresiden være lik <math>\arcsin</math> av venstresiden. Altså:
$\arcsin(\sin(bx))=\arcsin(\frac ca)$ Dette gir oss to uttrykk for <math>x</math>:
$bx=\arcsin(\frac ca)\,\vee\,\pi-bx=\arcsin(\frac ca)$
Sinus er periodisk i <math>2\pi</math> så vi må legge til en vilkårlig multippel av <math>2\pi</math> på hver side.
<math>bx+k\cdot2\pi=\arcsin(\frac ca)\,\vee\,\pi-bx+k\cdot2\pi=\arcsin(\frac ca)\,,\,k\in\mathbb{Z}</math>
- Når vi isolerer <math>x</math> på venstresiden får vi
- <math>x=\frac{\arcsin(\frac ca)-k\cdot2\pi}{b}\,\vee\,x=\frac{\arcsin(\frac ca)-\pi(2k+1)}{b}\,,\,k\in\mathbb{Z}</math>
Den samme fremgangsmåten kan benyttes på trigonometriske grunnlikninger med <math>\cos</math> og <math>\tan</math> også, men husk at disse har litt forskjellige egenskaper, så løsningene blir ikke de samme.
EKSEMPEL 1.
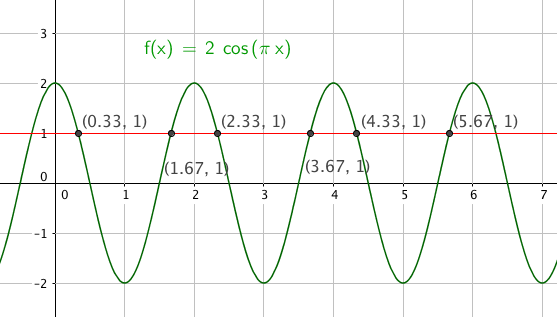
COS
$2cos(\pi x)=1 \quad \quad \quad x\in [0, 2\pi> $
$cos( \pi x) = \frac 12 \\ \pi x = \frac{\pi}{3} +k2\pi \vee \pi x $
$= 2\pi-\frac{\pi}{3} + k2\pi \\ x= \frac 13+2k \vee x=2- \frac13 +2k \\ x= \frac 13 \vee x= \frac 73 \vee x= \frac{13}{3} \vee x= \frac 53 \vee x= \frac{11}{3} \vee x= \frac{17}{3}$
$x \in${$ \frac{1}{3}, \frac{5}{3}, \frac{7}{3}, \frac{11}{3}, \frac{13}{3}, \frac{17}{3}$}
Slik ser det ut:
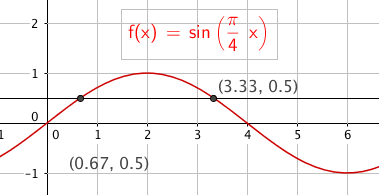
SIN
$sin( \frac{\pi}{4}x) = \frac 12 \quad \quad \quad x \in[0, 2 \pi> \\ \frac{\pi}{4}x = \frac{\pi}{6} +2k \pi \vee \frac{\pi}{4}x = \pi - \frac{\pi}{6} +2k \pi \\ x= \frac 23 +8k \vee x = 4- \frac 23 + 8k \\ x= \frac 23 \vee x = \frac{10}{3}$
$x \in ${$ \frac 23, \frac{10}{3}$}
Slik ser det ut:
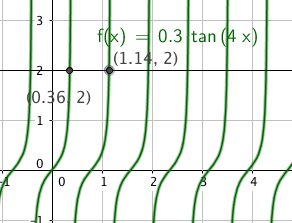
TAN
$0,3 tan(4x)= 2 \quad \quad \quad x \in [0, \frac{\pi}{2}> \\ tan(4x) = 6,667 \\ 4x = 1,42 + k \pi \\ x= 0,36 \vee x= 1,14$
$x \in ${ 0,36 , 1,14}
Slik ser det ut:
2)
$a cos^2 x + b cos x + c = 0 \quad $ eller $ \quad a sin^2 x + b sin x + c = 0$
Løses ved å erstatt cos x , eventuelt sin x, med u. Løser andregradsligningen og setter løsningen(e) lik cos x (eller sin x) og finner mulige x verdier.
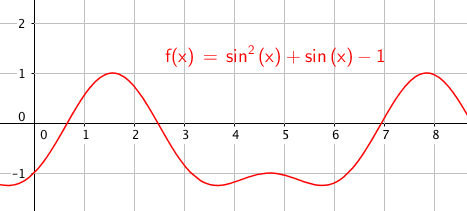
Eksempel 2.
<math>\sin^2x+\sin\,x-1=0\,,\,x\in[0,2\pi></math>
Setter sin x = u og bruker andregradsformelen, og får:
<math>\sin\,x=\frac{\sqrt{5}-1}{2}</math>
<math>\sin\,x=\frac{\sqrt{5}+1}{2}</math>
Merk at <math>\frac{\sqrt{5}+1}{2}>1</math>, altså har ikke denne grunnlikningen noen løsninger.
Vi står igjen med kun den første trigonometriske grunnlikningen. Når vi løser denne, får vi
$x= 0,67 \vee x= 2,48$
Slik ser det ut:
$x \in${0,67 , 2,48}
3)
Begge sider divideres med cos x (forskjellig fra null). Vi får da en identitet i tan x.
Eksempel 3.
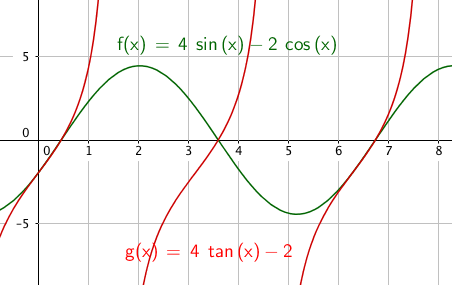
$4sinx-2cosx=0 \quad \quad x \in [0, 2 \pi>\\ 4tanx-2=0 \\ tanx = \frac 12 \\ x = tan^{-1}(\frac 12) = 0,46 + k \pi \\ x= 0,46 \vee x = 3,61$
$x \in$ {0,46 , 3,61}
Slik ser det ut:
4)
Ligningen løses ved å erstatte $sin^2x \quad $ med $1 - cos^2 x \quad$ eller $ cos^2 x \quad$ med $1 - sin^2 x$
Eksempel 4.
- <math>\sin\,x+2cos^2x=1\,,\,x\in[0,2\pi > </math>
- Vi kjenner identiteten <math>\sin^2x+\cos^2x=1</math>.
Den kan vi bruke her for å omforme ligningen til
- <math>\sin\,x+2-2\sin^2x=1</math>
- <math>2\sin^2x-\sin\,x-1=0</math>
- Dette er en andregradslikning i $\sin\,x$, som vi kan løse:
- <math>\sin\,x=\frac{1\pm\sqrt{1+8}}{4}=\frac{1\pm 3}{4}</math>
- <math>\sin\,x=\frac{1+3}{4}=1 \,\vee\,\sin\,x=\frac{1-3}{4}=-\frac12</math>
- <math>\sin\,x=1\,\Rightarrow\,x=\frac{\pi}{2}</math>
- <math>\sin\,x=-\frac12\,\Rightarrow\,x=\frac{7\pi}{6} \,\vee\,x=\frac{11\pi}{6}</math>
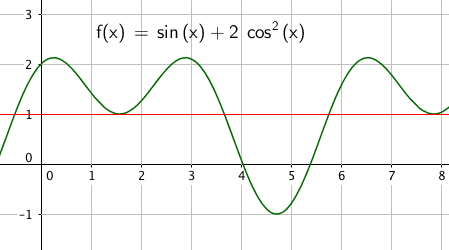
$x= \frac {\pi}{2} \vee x= \frac{7 \pi}{6} \vee x= \frac{11 \pi}{6}$
$x \in${$\frac {\pi}{2}, \frac{7 \pi}{6}, \frac{11 \pi}{6}$}
Slik ser det ut:
5)
Løses ved å dividere begge sider av likhetstegnet med $cos^2 x \quad \quad cos x \neq 0$
Eksempel 5.
$2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi>\\ 2tan^2x+3tanx-1=0 \\ 2u^2+3u-1=0$
$tan x =-1,06 \vee tanx = 0,27 \\x= -1,06 + k\pi \vee x= 0,27 + k\pi \\ x = 0,27 \vee x=3,45 \vee x=2,08 \vee x=5,22 $
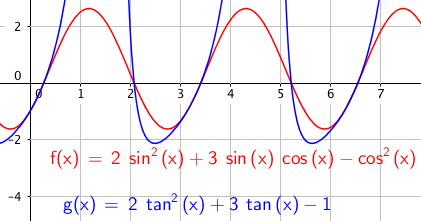
$x \in$ {0,27 , 2,08 , 3,45 , 5,22}
Slik ser det ut:
6)
Her må konstantleddet skrives om : $d = d \cdot 1 =d(sin^2 x + cos^2 x)$ . Ligningen løses nå som beskrevet i punktet over.
Eksempel 6.
$4sin^2x+ sinx cos x - 3cos^2x=3 \quad \quad x \in [0, 2\pi> \\4sin^2x+ sinx cos x - 3cos^2x = 3sin^2x + 3cos^2x \\ sin^2x + sinx cosx - 6cos^2 =0 \\ tan^2x + tanx - 6 = 0 \\ tanx = -3 \vee tanx = 2 \\ x= -1,24 +k\pi \vee x=1,11 + k\pi \\ x= 1,11 \vee x= 4,25 \vee x= 1,90 \vee x=5,04 $
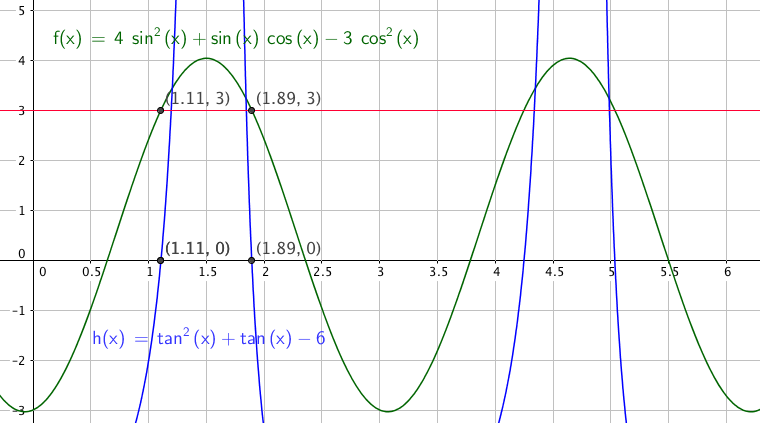
$x \in ${1,11 , 1,90 , 4,25 , 5,04}
Slik ser det ut:
7)
- <math>a\sin cx + bcos cx = d</math>
- <math> Asin (cx + \varphi)=d</math> der <math>A=\sqrt{a^2+b^2}</math> og <math>\varphi</math> er gitt ved <math> tan \varphi = \frac ba</math> og <math>\varphi</math>ligger i samme kvadrant som (a,b).
Eksempel 7.
- Eksempel:
Vinkelen <math>\varphi</math> ligger i første kvadrant, <math>\varphi =tan^{-1}(1)= \frac {\pi}{4} </math>
Vi får$\sqrt 2 sin(x + \frac \pi 4) = 1 \\ sin (x+ \frac \pi 4) = \frac{\sqrt 2}{2} \\ x + \frac {\pi}{4} = \frac {\pi}{4} +2k\pi \vee x + \frac{\pi}{4}= \pi - \frac{\pi}{4} +2k\pi \\ x=0 \vee x= \frac {\pi}{2}$
$x \in$ {0, $\frac \pi 2$}
Det ser slik ut:
8)
$a^2\pm ab= 0 \Rightarrow a( a \pm b)= 0$
a og b er sinx og cosx, eler cosx og sinx.
Eksempel 8.
Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnlikninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen
<math>\sin\,x\,\cos\,x-cos\,x=0\,,\,x\in [0,2\pi></math>
Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på <math>\cos\,x</math>. Generelt prøver man å ikke dele eller multiplisere med funksjoner av variabler, fordi du kan miste løsninger, eller lage falske løsninger. Dette gjelder generelt når du deler på null eller multipliserer med null. I stedet faktoriserer vi ligningen:
<math>\cos\,x\,(\sin\,x-1)=0</math>
- Nå ser vi at for at ligningen skal oppfylles, må <math>\cos\,x=0</math> eller <math>\sin\,x-1=0</math>. Vi har klart å redusere den kompositte trigonometriske ligningen til to trigonometriske grunnlikninger.
- <math>\sin\,x=1 \,\Rightarrow\, x=\frac{\pi}{2}</math>
- <math>\cos\,x=0 \,\Rightarrow\, x=\frac{\pi}{2} \,\vee\, x=\frac{3\pi}{2}</math>
$ x \in${$\frac{\pi}{2} , \frac{3\pi}{2}$}
- NB: Dersom du på forhånd har sjekket at det du deler eller multipliserer med ikke er lik null, er det greit å gjennomføre operasjonen. Dette kan gjøres ved å plugge inn null for den aktuelle faktoren og se om likningen oppfylles.