Trigonometriske likninger: Forskjell mellom sideversjoner
| (71 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 1: | Linje 1: | ||
Det finnes forskjellige typer trigonometriske | Det finnes forskjellige typer trigonometriske likninger og ofte er det forskjellige måter å løse dem på. Nedenfor følger en oversikt over de vanligste typene og et forslag til hvordan de kan løses. | ||
Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende: | Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende: | ||
| Linje 9: | Linje 9: | ||
: | : | ||
===Trigonometriske | ===1. Trigonometriske grunnlikninger=== | ||
Trigonometriske | Trigonometriske likninger som kun involverer én trigonometrisk funksjon, kaller vi trigonometriske grunnlikninger. Disse er de enkleste trigonometriske likningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser. | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Løsningsmetode for trigonometriske grunnlikninger''' | |||
Vi tar for oss ligningen | |||
$a\sin(bx)=c$ | |||
Vi vil løse denne ligninger for | |||
$\sin(bx)=\frac ca$ | |||
Siden høyresiden er lik venstresiden, vil | |||
$\arcsin(\sin(bx))=\arcsin(\frac ca)$ | |||
Dette gir oss to uttrykk for | |||
$bx=\arcsin(\frac ca)\,\vee\,\pi-bx=\arcsin(\frac ca)$ | |||
Sinus er periodisk i | |||
:Når vi isolerer | :Når vi isolerer | ||
:: | :: | ||
Den samme fremgangsmåten kan benyttes på trigonometriske | Den samme fremgangsmåten kan benyttes på trigonometriske grunnlikninger med | ||
</div> | </div> | ||
==='''EKSEMPEL 1.'''=== | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
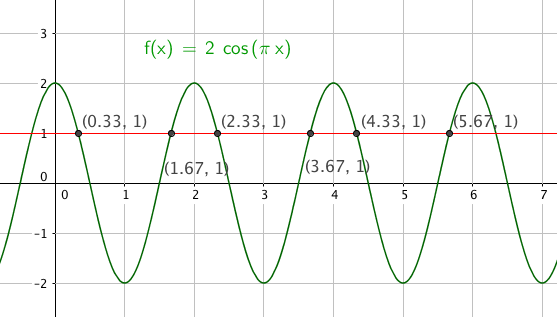
'''COS''' | |||
== | $cos( \pi x) = \frac 12 \ \pi x = \frac{\pi}{3} +k2\pi \vee \pi x $ | ||
$ | $x \in${$ \frac{1}{3}, \frac{5}{3}, \frac{7}{3}, \frac{11}{3}, \frac{13}{3}, \frac{17}{3}$} | ||
Slik ser det ut: | |||
[[Bilde:Trig-3-4-3-11.png]] | [[Bilde:Trig-3-4-3-11.png]] | ||
'''SIN''' | |||
Slik ser det ut: | |||
[[Bilde:Trig-3-4-3-12.png]] | [[Bilde:Trig-3-4-3-12.png]] | ||
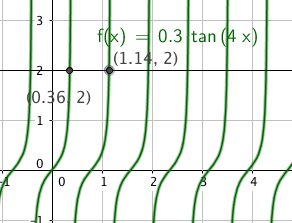
'''TAN''' | |||
Slik ser det ut: | |||
[[Bilde:Trig-3-4-3-13.png]] | [[Bilde:Trig-3-4-3-13.png]] | ||
| Linje 50: | Linje 85: | ||
</div> | </div> | ||
=== | ===2)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 59: | Linje 94: | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 2.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| Linje 71: | Linje 106: | ||
Merk at | Merk at | ||
Vi står igjen med kun den første trigonometriske | Vi står igjen med kun den første trigonometriske grunnlikningen. Når vi løser denne, får vi | ||
| Linje 85: | Linje 120: | ||
</div> | </div> | ||
=== | ===3)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 94: | Linje 129: | ||
</div> | </div> | ||
===Eksempel 3.=== | |||
===Eksempel | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
| Linje 107: | Linje 141: | ||
</div> | </div> | ||
=== | ===4)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 113: | Linje 147: | ||
Ligningen løses ved å erstatte $ | Ligningen løses ved å erstatte $sin^2x \quad | ||
</div> | </div> | ||
==='''Eksempel | ==='''Eksempel 4.'''=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
::: | ::: | ||
::Vi kjenner identiteten | ::Vi kjenner identiteten | ||
Den kan vi bruke her for å omforme ligningen til | |||
::: | ::: | ||
| Linje 128: | Linje 164: | ||
::: | ::: | ||
::Dette er en andregradslikning i | ::Dette er en andregradslikning i $\sin\,x$, som vi kan løse: | ||
::: | ::: | ||
| Linje 140: | Linje 176: | ||
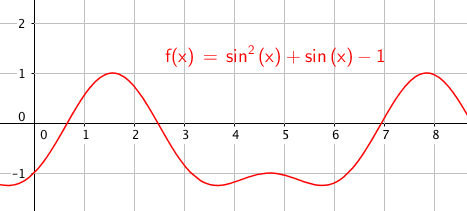
Slik ser det ut: | Slik ser det ut: | ||
| Linje 146: | Linje 184: | ||
</div> | </div> | ||
=== | ===5)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
Løses ved å dividere begge sider av likhetstegnet med | Løses ved å dividere begge sider av likhetstegnet med $cos^2 x \quad \quad cos x \neq 0$ | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 5.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
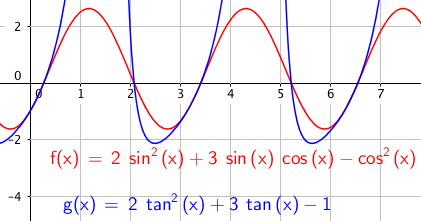
$2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi>\ 2tan^2x+3tanx-1=0 \ 2u^2+3u | $2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi>\ 2tan^2x+3tanx-1=0 \ 2u^2+3u-1=0$ | ||
$tan x =-1,06 \vee tanx = 0,27 \x= -1,06 + k\pi \vee x= 0,27 + k\pi \ x = 0,27 \vee x=3,45 \vee x=2,08 \vee x=5,22 $ | |||
Slik ser det ut: | Slik ser det ut: | ||
| Linje 168: | Linje 207: | ||
</div> | </div> | ||
=== | ===6)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 175: | Linje 214: | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 6. === | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
[[Bilde:Trig-3-4-3- | |||
Slik ser det ut: | |||
[[Bilde:Trig-3-4-3-14.png]] | |||
</div> | </div> | ||
=== | ===7)=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;">Likninger av typen<p></p> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;">Likninger av typen<p></p> | ||
::: | ::: | ||
Løses ved å skrive om til: <p></p> | Løses ved å skrive om til: <p></p> | ||
::: | ::: | ||
</div> | </div> | ||
===Eksempel | ===Eksempel 7.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
:'''Eksempel:'''<p></p> | :'''Eksempel:'''<p></p> | ||
<math>sin x + cos x = 1 \quad \quad \quad x\in [0,2\pi></math> <p></p> | |||
Vinkelen | Vinkelen | ||
| Linje 205: | Linje 249: | ||
<p></p>Vi får<p></p> | <p></p>Vi får<p></p> | ||
$\sqrt 2 sin(x + \frac \pi 4) = 1 \ sin (x+ \frac \pi 4) = \frac{\sqrt 2}{2} \ x + \frac {\pi}{4} = \frac {\pi}{4} +2k\pi \vee x + \frac{\pi}{4}= \pi - \frac{\pi}{4} +2k\pi \ x=0 \vee x= \frac {\pi}{2}$ | |||
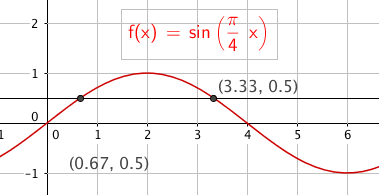
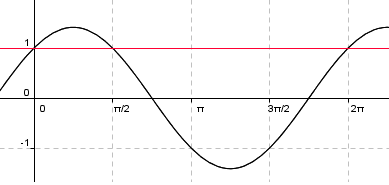
Det ser slik ut: | |||
[[Bilde:sincos.png]] | [[Bilde:sincos.png]] | ||
| Linje 211: | Linje 260: | ||
</div> | </div> | ||
===8)=== | |||
=== | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
| Linje 221: | Linje 269: | ||
</div> | </div> | ||
=== Eksempel | === Eksempel 8.=== | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske | Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnlikninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen | ||
Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på | Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på | ||
:Nå ser vi at for at ligningen skal oppfylles, må | :Nå ser vi at for at ligningen skal oppfylles, må | ||
:: | :: | ||
Siste sideversjon per 8. aug. 2023 kl. 03:33
Det finnes forskjellige typer trigonometriske likninger og ofte er det forskjellige måter å løse dem på. Nedenfor følger en oversikt over de vanligste typene og et forslag til hvordan de kan løses.
Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende:
1. Trigonometriske grunnlikninger
Trigonometriske likninger som kun involverer én trigonometrisk funksjon, kaller vi trigonometriske grunnlikninger. Disse er de enkleste trigonometriske likningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser.
Løsningsmetode for trigonometriske grunnlikninger
Vi tar for oss ligningen
Vi vil løse denne ligninger for
Siden høyresiden er lik venstresiden, vil
Sinus er periodisk i
- Når vi isolerer
Den samme fremgangsmåten kan benyttes på trigonometriske grunnlikninger med
EKSEMPEL 1.
2)
Løses ved å erstatt cos x , eventuelt sin x, med u. Løser andregradsligningen og setter løsningen(e) lik cos x (eller sin x) og finner mulige x verdier.
Eksempel 2.
Setter sin x = u og bruker andregradsformelen, og får:
Merk at
Vi står igjen med kun den første trigonometriske grunnlikningen. Når vi løser denne, får vi
Slik ser det ut:
3)
Begge sider divideres med cos x (forskjellig fra null). Vi får da en identitet i tan x.
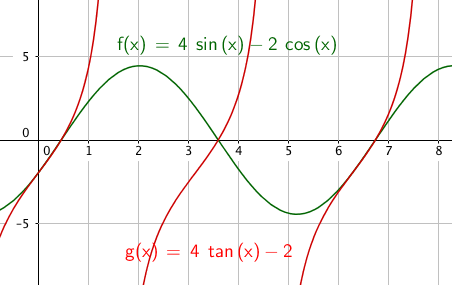
Eksempel 3.
4)
Ligningen løses ved å erstatte
Eksempel 4.
- Vi kjenner identiteten
- Vi kjenner identiteten
Den kan vi bruke her for å omforme ligningen til
- Dette er en andregradslikning i
- Dette er en andregradslikning i
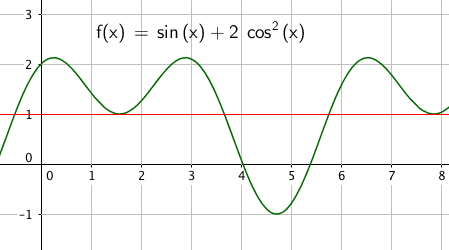
Slik ser det ut:
5)
Løses ved å dividere begge sider av likhetstegnet med
Eksempel 5.
6)
Her må konstantleddet skrives om :
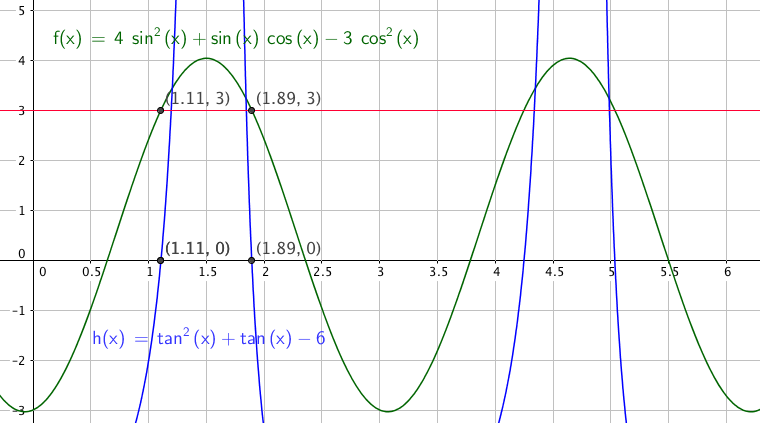
Eksempel 6.
7)
Eksempel 7.
8)
a og b er sinx og cosx, eler cosx og sinx.
Eksempel 8.
Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnlikninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen
Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på
- Nå ser vi at for at ligningen skal oppfylles, må
- NB: Dersom du på forhånd har sjekket at det du deler eller multipliserer med ikke er lik null, er det greit å gjennomføre operasjonen. Dette kan gjøres ved å plugge inn null for den aktuelle faktoren og se om likningen oppfylles.