Potenser og logaritmer: Forskjell mellom sideversjoner
| (10 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 542: | Linje 542: | ||
'''Eksempel 24:''' | '''Eksempel 24:''' | ||
<br> For å regne ut eller forenkle, der man har flere tall på standardform i samme uttrykk, bruker man potensreglene: <p></p><math>\frac{2\cdot 10^{-23}\cdot 6 \cdot 10^{47}}{8 \cdot 10^{-5}}= \frac{2 \cdot 6}{8} \cdot 10^{-23+47-(-5)}=\frac{12}{8}\cdot 10^{29}=1,5 \cdot 10^{29}</math> | <br> For å regne ut eller forenkle, der man har flere tall på standardform i samme uttrykk, bruker man potensreglene: <p></p><math>\frac{2\cdot 10^{-23}\cdot 6 \cdot 10^{47}}{8 \cdot 10^{-5}}= \frac{2 \cdot 6}{8} \cdot 10^{-23+47-(-5)}=\frac{12}{8}\cdot 10^{29}=1,5 \cdot 10^{29}</math> | ||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |||
:[https://youtu.be/_zNlxt-Lap4 '''Video eksempel:''' Regner med standardform] | |||
</div> | </div> | ||
| Linje 570: | Linje 577: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel 25:''' | |||
<math> log 100^{24} = 24 \cdot log 100 =24 \cdot 2 = 48 </math> | <math> log 100^{24} = 24 \cdot log 100 =24 \cdot 2 = 48 </math> | ||
| Linje 588: | Linje 598: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel 26:''' | |||
<math> log (10\cdot 100) = log 10 + log 100 = 1 + 2 = 3 </math><br><br> | <math> log (10\cdot 100) = log 10 + log 100 = 1 + 2 = 3 </math><br><br> | ||
10 ganger 100 er 1000. Logaritmen til 1000 er 3. Man ser at formelen stemmer. | 10 ganger 100 er 1000. Logaritmen til 1000 er 3. Man ser at formelen stemmer. | ||
| Linje 605: | Linje 619: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel 27:''' | |||
<math> log \frac {10.000}{100} = log 10.000 - log 100 = 4-2 = 2</math><br><br> | <math> log \frac {10.000}{100} = log 10.000 - log 100 = 4-2 = 2</math><br><br> | ||
Titusen delt på hundre er hundre.Logaritmen til hundre er to. | Titusen delt på hundre er hundre.Logaritmen til hundre er to. | ||
| Linje 612: | Linje 630: | ||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85F%2B860%2B861%2B862%2B863%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=85F%2B860%2B861%2B862%2B863%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
== Bruk av regneregler for logaritmer == | === Bruk av regneregler for logaritmer === | ||
I praktisk oppgaveregning får man ofte bruk for å kombinere de tre reglene over. Her er et par eksempler:<br><br> | I praktisk oppgaveregning får man ofte bruk for å kombinere de tre reglene over. Her er et par eksempler:<br><br> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<br> | '''Eksempel 28:'''<br> | ||
Vis at <math>3logx - log 8x +3log2-logx^2 = 0 </math><br><br> | Vis at | ||
<math>3logx - log 8x +3log2-logx^2 = 0 </math><br><br> | |||
<math>3logx - (log 8 + log x) +log2^3- 2logx = </math><br><br> | <math>3logx - (log 8 + log x) +log2^3- 2logx = </math><br><br> | ||
<math>3logx - log 8 - log x + log 8 - 2logx = 0 </math> | <math>3logx - log 8 - log x + log 8 - 2logx = 0 </math> | ||
| Linje 625: | Linje 645: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<br> | '''Eksempel 29:'''<br> | ||
Skriv enklest mulig: | Skriv enklest mulig: | ||
<math>log(3x) - log x^3 - log(\frac3x)+ 2logx</math><br><br> | <math>log(3x) - log x^3 - log(\frac3x)+ 2logx</math><br><br> | ||
<math> (log3 + log x) - 3log x - (log 3 - log x)+ 2logx = </math><br><br> | <math> (log3 + log x) - 3log x - (log 3 - log x)+ 2logx = </math><br><br> | ||
<math> log3 + log x - 3log x - log 3 + log x + 2logx = log x </math><br><br> | <math> log3 + log x - 3log x - log 3 + log x + 2logx = log x </math><br><br> | ||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |||
:[https://youtu.be/uhY7yUKjeGE '''Video eksempel:''' Forenkling av logaritmeuttrykk] | |||
</div> | </div> | ||
| Linje 652: | Linje 678: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' | '''Eksempel 30:''' | ||
<br> | <br> | ||
Du vil nok oppleve at de fleste kalkulatorer har problemer med andre baser enn 10 og e, men et enkelt eksempel illustrerer sammenhengen.<br> | Du vil nok oppleve at de fleste kalkulatorer har problemer med andre baser enn 10 og e, men et enkelt eksempel illustrerer sammenhengen.<br> | ||
| Linje 668: | Linje 694: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<br><br> | '''Eksempel 31:'''<br><br> | ||
Hva er logaritmen til 16807, med 7 som base?<br><br> | Hva er logaritmen til 16807, med 7 som base?<br><br> | ||
<math>log_7 16807 = \frac{log_{10} 16807}{ log_{10} 7 } = 5 </math><br> | <math>log_7 16807 = \frac{log_{10} 16807}{ log_{10} 7 } = 5 </math><br> | ||
| Linje 698: | Linje 724: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' | '''Eksempel 32:''' | ||
<br> | |||
Konsentrasjonen av <math> H^+ </math> ioner i et avløp fra en bedrift måles over en periode på 3 år og gir følgende gjennomsnittsresultater: <br> | Konsentrasjonen av <math> H^+ </math> ioner i et avløp fra en bedrift måles over en periode på 3 år og gir følgende gjennomsnittsresultater: <br> | ||
| Linje 727: | Linje 753: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' | '''Eksempel 33:''' | ||
<br> | <br> | ||
Hva er konsentrasjonen av <math>H^+ </math> ioner i en løsning der pH er 13?<br><br> | Hva er konsentrasjonen av <math>H^+ </math> ioner i en løsning der pH er 13?<br><br> | ||
| Linje 736: | Linje 762: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' | '''Eksempel 34:''' | ||
<br> | <br> | ||
Hva er pH dersom konsentrasjonen av <math>H^+ </math> i løsningen er <math>5,7 \cdot 10^{-9} </math>?<br><br> | Hva er pH dersom konsentrasjonen av <math>H^+ </math> i løsningen er <math>5,7 \cdot 10^{-9} </math>?<br><br> | ||
| Linje 838: | Linje 864: | ||
</div> | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |||
:[https://youtu.be/jaLqqvWGd44 '''Video eksempel:''' Løsning av logaritmelikninger] | |||
</div> | |||
Siste sideversjon per 2. apr. 2023 kl. 13:50
Potenser uten brøkeksponent
Innledning
1000 kan skrives som 10 · 10 · 10 og 100 som 10 · 10. Noen ganger ønsker man å skrive tallene på denne måten. Å skrive 1.000.000 som 10 · 10 · 10 · 10 · 10 · 10 er både plasskrevende og tungvindt. Man innfører derfor en ny måte å skrive tall på, og vi kalle den for potens.
Eksempel 1
$1000 = 10\cdot 10\cdot10 = 10^3$
En potens består av et grunntall og en eksponent.
Grunntallet i dette tilfellet
er 10
og eksponenten er 3. Eksponenten forteller oss hvor mange ganger grunntallet skal ganges
med seg selv.
Eksempel 2
| Tall | 100000 | 10000 | 1000 | 100 | 10 | 1 | 0,1 | 0,01 | 0,001 |
| Potens | <math> 10^5 </math> | <math> 10^4 </math> | <math>10^3 </math> | <math>10^2 </math> | <math>10^1 </math> | <math>10^0 </math> | <math>10^ {-1} </math> | <math>10^{-2} </math> | <math>10^{-3} </math> |
Eksempel 3
<math>10^9 = 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot10 \cdot 10 \cdot 10 = 1 000 000 000</math>
Som man ser fra eksempel tre kan potenser ha andre grunntall enn ti.
Regneregler for potenser uten brøkesponent
Reglene nedenfor gjelder kun når potensene har samme grunntall.
Multiplikasjon av potenser
Dersom man skal multiplisere <math>4^3</math> med <math>4^4</math> får man;<math>4^3\cdot 4^4= 4\cdot4\cdot4\cdot4\cdot4\cdot4\cdot4 = 4^{3+4}</math>
Den generelle regel for potensmultiplikasjon er:
<math>a^n \cdot a^m = a^{n+m}</math>
Eksempel 4
<math>a^3 \cdot a^2=a^{3+2} = a^5</math>
Divisjon av potenser
Den generelle regel for potensdivisjon er:
<math> \frac{a^n}{a^m} = a^{n-m}</math>
Eksempel 5
<math> \frac{a^3}{a^2} =a^{3-2} = a^1 =a</math>
Potens av potenser
<math> (a^n)^m = a^{n\cdot m}</math>
Eksempel 6
<math> (a^3)^2=a^{3 \cdot 2}= a^6</math>
Tall i nulte
Alle tall (og bokstaver) opphøyd i null er per. definisjon lik 1.
<math> a^0=1</math>
Eksempel 7
<math> \frac{x^5 \cdot x^2}{x^7} = x^{5+2-7}=x^0=1 </math>
Negativ eksponent
<math> a^{-n}= \frac{1}{a^n}</math>
Eksempel 8
<math> 2^{-3}= \frac{1}{2^3} =\frac{1}{8}</math>
Divisor og divident med samme eksponent og forskjellig grunntall
<math> \frac{a^m}{b^m} = (\frac{a}{b})^m </math>
Eksempel 9
<math> \frac{2^5}{7^5} = (\frac{2}{7})^5 </math>
Faktorer med samme eksponent og forskjellige grunntall
<math> a^m \cdot b^m = (ab)^m </math>
Eksempel 10
<math> 3^5 \cdot x^5 = (3x)^5 </math>
Sammensatte problemer
Ofte får man regnestykker der man må kombinere to eller flere regneregler. Her er et par eksempler:
Eksempel 11
<math> \frac{(3^5)^{-2} \cdot 3^{4}}{9^{-1}} = \frac{3^{-10} \cdot 3^{4}}{3^{-2}} = 3^{-10+4-(-2)} = 3^{-4}= \frac{1}{3^4} = \frac{1}{81} </math>
Eksempel 12
<math> \frac{(a^2b^4)^{3} \cdot b \cdot (a^{-2}b^5)^{-1}}{a^{-2}b^9} = \frac{a^6b^{12} \cdot b \cdot a^{2}b^{-5}}{a^{-2}b^9} = a^{6+2-(-2)}b^{12+1+(-5)-9} = a^{10}b^{-1} = \frac {a^{10}}{b} </math>
Kvadratrot
Kvadratroten av et tall m, er et tall n som ganget med seg selv gir m, og skrives $ \sqrt {m} $
Hva er kvadratroten av 4? Tallet som ganget med seg selv gir 4 er 2. Det skrives slik:
<math>\sqrt {4}= \sqrt {2 \cdot 2} = 2 </math>
Mer generelt: dersom n·n = m så er: <math>\sqrt{m}= \sqrt{n \cdot n} = n </math>
Man kan ikke ta kvadratroten av et negativt tall.
Ut fra navnet kvadratrot er det naturlig å tro et det er en sammenheng mellom kvadratrot og kvadrat. La oss se!
Et kvadrat har sidekanter med lengde k.
Arealet av kvadratet er k · k, eller k <math>^2</math>. Dersom man setter k = 10 cm betyr det at arealet av kvadratet er 100cm <math>^2</math>. Dersom man kjenner arealet av et kvadrat kan vi bruke kvadratroten til å finne lengden av sidekantene.
Et kvadrat med areal 81 cm <math>^2</math> har sidekanter med lengde:
<math>L = \sqrt{81cm^2}=9cm</math>
Kvadratroten kalles av og til for andreroten og kan også skrives slik:
<math> \sqrt{x}=\sqrt[2]{x}</math>
Det er nyttig å vite dette, men man bruker <math> \sqrt{x}</math> når man ønsker å skrive kvadratroten av x.
n'terot
På samme måten som man kan ta kvadratroten, eller andreroten av at tall, er det også mulig å ta tredjeroten. Tenk deg en terning med sidekanter k. Vi setter k = 5cm. Volumet av terningen blir V = k <math>^3</math> =k · k · k = 5cm · 5cm · 5cm = 125cm <math>^3</math>.
Tredjeroten, eller kubikkroten som den også kalles, kan man bruke til å finne sidekanten av en terning dersom man kjenner volumet. Eksemplet over løser man på følgende måte:
<math>\sqrt[3]{124cm^3}</math>
Når man skal finne tredjeroten jakter vi på det tallet som, ganget med seg selv tre ganger, har et produkt tilsvarende tallet under rottegnet. Vi kan skrive et generelt utrykk slik:
<math>\sqrt[n]{a}</math>
Her må n være et helt positivt tall. Dersom n = 2 (kvadratrot) pleier vi utelate 2 - tallet.
<math>\sqrt[4]{16} = \sqrt[4]{2 \cdot2 \cdot2 \cdot 2} =2 </math>
<math>\sqrt[5]{x^5} = \sqrt[5]{x \cdot x \cdot x \cdot x \cdot x} =x </math>
Rot som potens & brøk eksponent
Regneregler
$ \sqrt[n]{a}= a^{\frac{1}{n}} $
Eksempel 13
$ \sqrt [5]{32}= 32^{\frac{1}{5}} = (2^5) ^{\frac 1 5} =2 $
$a^{\frac{m}{n}}= \sqrt[n]{a^m} = (\sqrt[n]{a})^m $
Eksempel 14
$ 27^{\frac{2}{3}}= \sqrt[3]{27^2} = (\sqrt[3]{27})^2 = 3^2 = 9$
$(ab)^{\frac1n}=\sqrt[n]{a \cdot b} =\sqrt[n]{a}\cdot \sqrt[n]{b} $
Eksempel 15
$ (16x^8)^{\frac14}=\sqrt[4]{16 \cdot x^8} =\sqrt[4]{16}\cdot \sqrt[4]{x^8}
=\sqrt[4]{2 \cdot 2\cdot 2 \cdot2}\cdot \sqrt[4]{x \cdot x \cdot x\cdot x\cdot x \cdot x \cdot x \cdot x} = 2x^2 $
$( \frac ab)^{\frac 1n} =\sqrt[n]{\frac ab}= \frac{\sqrt[n]{a}}{\sqrt[n]{a}} $
Eksempel 16
$ ( \frac {8}{27})^{\frac 13} =\sqrt[3]{\frac {8}{27}}= \frac{2}{3} $
Samensatte problemer
Ofte er en kombinasjon av flere regler nødvendig for å løse et problem:
Skriv <math> \sqrt{a} \cdot a^{\frac{2}{3}} \cdot a^{- \frac {1}{6}}</math> enklest mulig.
<math> \sqrt{a} \cdot a^{\frac{2}{3}} \cdot a^{- \frac {1}{6}} =
a^{\frac{1}{2}+ \frac {2}{3} - \frac {1}{6}} =
a^{\frac{3}{6}+ \frac {4}{6} - \frac {1}{6}} =
a^{\frac{6}{6}} = a
</math>
<math> \frac{\sqrt[3]{a} \cdot \sqrt[4]{a} } {( \sqrt[12]{a})^5 } =
\frac{a^{\frac13} \cdot a^ {\frac14} } {a^{\frac{5}{12}} } =
a^{\frac13+\frac14-\frac{5}{12}}= a^{\frac{4}{12}+\frac{3}{12}-\frac{5}{12}}= a^{\frac{2}{12}}
= a^{\frac{1}{6}}= \sqrt[6]{a}
</math>
<math> \frac {(3a)^{\frac12} \cdot (3\sqrt{a})^{\frac{2}{3}}}{a^{-\frac 12}\cdot (3a^5)^{\frac16}} =
3^{\frac{1}{2}+ \frac {2}{3} - \frac {1}{6}}\cdot a^{\frac{1}{2}+ \frac {2}{6} -(- \frac {1}{2})- \frac56} =
3^{\frac{3}{6}+ \frac {4}{6} - \frac {1}{6}}\cdot a^{\frac{3}{6}+ \frac {2}{6} + \frac {3}{6}- \frac56} = 3 \cdot a^{ \frac 12} = 3 \cdot \sqrt a
</math>
Standardform
Det er plassbesparende å skrive store og små tall på standardform.
Man kan skrive 100 som <math>10^2</math>, men hva med 300? 300 kan skrives som <math>3 \cdot 100</math>, som kan skrives som <math>3 \cdot 10^2</math>. På samme måte kan for eksempel 320 skrives som <math>3,2 \cdot 10^2</math>.
Dette kaller man standardform.
Generelt ser formelen slik ut:
<math>
\pm k \cdot10^n </math>
Der n er et helt tall og 1≤ k < 10.
Eksempel 20:
Skriv 320000 på standardform.
Løsning:
Komma flyttes fem plasser mot venstre og man får<math>3,2 \cdot 10^5</math>
Eksempel 21:
Skriv 0,00000012 på standardform.
Løsning:
Komma flyttes syv plasser mot høyre og man får<math>1,2 \cdot 10^{-7}</math>
Eksempel 22:
For å ionisere et hydrogenatom trengs det en energimengde på 0,000 000 000 000 000 00218
Eksempel 23:
Utfør multiplikasjonen og skriv på standardform: <math>2,5 \cdot 10^{4} \cdot 5000</math>
Løsning:
<math>2,5 \cdot 10^{4} \cdot 5,0 \cdot 10^3 = 2,5 \cdot 5,0 \cdot 10^{4} \cdot 10^3 = 12,5 \cdot 10^{4+3} =12,5 \cdot 10^{7} </math> Legg merke til at man multipliserer tallene foran tierpotensene for seg, og brukerer regneregler for potenser på tierpotensene. Svaret over er ikke på standardform fordi 12,5 er større enn 10. Man flytter komma en plass mot venstre og øker eksponenten med en. Da får man at:<math>12,5 \cdot 10^{7} = 1,25 \cdot 10^{8} </math>
Eksempel 24:
For å regne ut eller forenkle, der man har flere tall på standardform i samme uttrykk, bruker man potensreglene: <math>\frac{2\cdot 10^{-23}\cdot 6 \cdot 10^{47}}{8 \cdot 10^{-5}}= \frac{2 \cdot 6}{8} \cdot 10^{-23+47-(-5)}=\frac{12}{8}\cdot 10^{29}=1,5 \cdot 10^{29}</math>
Logaritmer
Innledning
Logaritmeregningen ble introdusert av Napier rundt 1614, og arbeidet ble fullført av Briggs i 1628. Logaritmetabellene som de utviklet har vært i bruk helt fram til vår tid. Før kalkulatorer og regnemaskinenes tid spilte logaritmer en sentral rolle fordi de forenklet utregningen. Selv om man ikke er så avhengig av disse forenklingene i dag brukes logaritmer fortsatt, blant annet diagrammer der verdiene spenner over flere dekadiske enheter (1, 10, 100, 1000, ....).
Regneregler
Logaritmen til et tall x med basis b er definert som den inverse funksjonen til <math>b^x</math> (b opphøyd i x). En logaritme kan ha forskjellige basiser eller grunntall (større enn null og ikke lik en). Det vanligste grunntallet for en logaritme er 10 og betegnelsen er log eller lg.(Den naturlige logaritmen ln har grunntall e og behandles separat.) Dersom andre grunntall brukes er det spesifisert, for eksempel dersom grunntallet er 2 skrives det slik: <math>log_2 x</math>.
Logaritmer med grunntall 10 kalles den briggske logaritmen , etter matematikeren Henry Briggs. Vi har følgende definisjon:
<math>10^{log a} = a </math>
<math>log 1000 = 3\qquad \text{fordi} \qquad 10^3 = 1000 </math>
<math>log 1 = 0 \qquad \text{fordi} \qquad 10^0 = 1 </math>
<math>log 0,01 = -2 \qquad \text{fordi} \qquad 10^{-2} = 0,01 </math>
Man kan ikke ta logaritmen til et negativt tall.
Logaritmen av en potens
<math> \log a^x = x \cdot \log a </math>
Eksempel 25:
<math> log 100^{24} = 24 \cdot log 100 =24 \cdot 2 = 48 </math>
Logaritmen av et produkt
<math> log (a\cdot b) = log a + log b </math>
Eksempel 26:
<math> log (10\cdot 100) = log 10 + log 100 = 1 + 2 = 3 </math>
10 ganger 100 er 1000. Logaritmen til 1000 er 3. Man ser at formelen stemmer.
Logaritmen av en brøk
<math> log \frac ab = log a - log b </math>
Eksempel 27:
<math> log \frac {10.000}{100} = log 10.000 - log 100 = 4-2 = 2</math>
Titusen delt på hundre er hundre.Logaritmen til hundre er to.
Bruk av regneregler for logaritmer
I praktisk oppgaveregning får man ofte bruk for å kombinere de tre reglene over. Her er et par eksempler:
Eksempel 28:
Vis at
<math>3logx - log 8x +3log2-logx^2 = 0 </math>
<math>3logx - (log 8 + log x) +log2^3- 2logx = </math>
<math>3logx - log 8 - log x + log 8 - 2logx = 0 </math>
Eksempel 29:
Skriv enklest mulig:
<math>log(3x) - log x^3 - log(\frac3x)+ 2logx</math>
<math> (log3 + log x) - 3log x - (log 3 - log x)+ 2logx = </math>
<math> log3 + log x - 3log x - log 3 + log x + 2logx = log x </math>
Endring av base (grunntall)
Det vanligste er å bruke 10 eller e som base, men et hvilket som helst tall kan i utgangspunktet brukes som base. Gitt en base b gjelder
<math> b^{log_bx} = x </math>
Ønsker så å skifte til base a:
<math>log_a( b^{log_bx}) = log_a( x) </math>
<math>(log_bx) \cdot (log_a b)= log_a( x) </math>
<math> log_bx = \frac{log_a( x)}{ log_a b } </math>
alle a, b og x er positive størrelser
Eksempel 30:
Du vil nok oppleve at de fleste kalkulatorer har problemer med andre baser enn 10 og e, men et enkelt eksempel illustrerer sammenhengen.
<math> 3 \cdot 3 \cdot 3 \cdot 3 = 81 </math> , dvs. logaritmen til 81 er 4 dersom basen er 3, eller
<math> log_381 =4 </math>
Dersom man bruker formelen over får man:
<math> log_381 = \frac{log_{10}81}{log_{10}3} = 4</math>
Eksempel 31:
Hva er logaritmen til 16807, med 7 som base?
<math>log_7 16807 = \frac{log_{10} 16807}{ log_{10} 7 } = 5 </math>
Svaret kan lett verifiseres ved å regne ut <math> 7^5</math>
Praktisk bruk
Surhetsgrad – pH
Et mol stoff er 6,022045· 1023 (avogadros tall) partikler. Mol per liter [M] brukes som et mål på konsentrasjon i væsker.
pH er definert som den negative logaritmen til konsentrasjonen av <math>H^+ (H_3O^+)</math> ioner i en løsning:
<math> pH = - lg (H^+) </math>
pH 7 er nøytralt mens pH mindre enn 7 er surt. pH over 7 er basisk.
Dersom man bruker definisjonen finner man at
<math> pH 14 = 0,00000000000001M = 1\cdot 10^{-14} M </math>
<math> pH 7 = 0,0000001M = 1 \cdot 10^{-7} M </math>
<math> pH 0 = 1,0 M = 1 \cdot 10^0 M </math>
Eksempel 32:
Konsentrasjonen av <math> H^+ </math> ioner i et avløp fra en bedrift måles over en periode på 3 år og gir følgende gjennomsnittsresultater:
1. år - 0,035 M
2. år - 0,00015 M
3. år - 0,000095 M
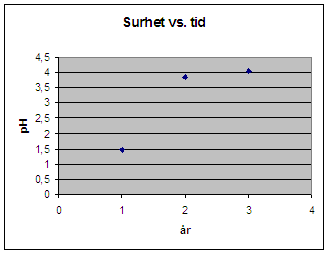
Nå kan man prøve å plotte resultatene direkte i et diagram, men man vil fort finne ut at man får problemer med skalaen fordi det er stor forskjell på observasjonene. Finner man pH de tre årene får man følgene resultater:
1. år - 0,035 M pH = - lg (0,035) = 1,5
2. år - 0,00015 M pH = - lg ( 0,00015) = 3,8
3. år - 0,000095 M pH = - lg (0,000095) = 4,0
Verdiene lar seg lettere plotte lineært når de er behandlet logaritmisk, i forhold til definisjonen for pH. Dersom du prøver å plotte konsentrasjonen direkte vil du få et problem med skalaen på aksene.
Eksempel 33:
Hva er konsentrasjonen av <math>H^+ </math> ioner i en løsning der pH er 13?
<math>13 = -lgC</math>
<math>c = 1 \cdot 10^{-13} </math>
Eksempel 34:
Hva er pH dersom konsentrasjonen av <math>H^+ </math> i løsningen er <math>5,7 \cdot 10^{-9} </math>?
<math>pH = - log(5,7 \cdot 10^{-9}) = 8,2</math>
Lyd - dB
Lyd
Lydstyrke måles I desibel, dB. Lyd er energi per flate og intensiteten på den svakeste lyden man kan høre er:
<math>I_0 = 10^{-12} [W/m^2] </math>
Dersom en lyd har intensiteten I er lydstyrken L, i desibel, gitt som
<math>L =10logI - 10logI_0 = 10logI + 120 </math>
Eksempel
Hva er lydintensiteten dersom lydstyrken er 60dB?
<math>L = 10logI + 120 </math>
<math>logI = \frac{L-120}{10} = \frac{60-120}{10} = -6 </math>
<math>I = 10^{-6} = 0,000001 [W/m^2] </math>
Eksempel
Hva er lydstyrken dersom intensiteten er <math>3,7 \cdot 10^{-3}[W/m^2] </math>?
<math>L = 10lg(3,7 \cdot 10^{-3}) + 120 = 96dB </math>
Eksempel
Hva skjer med lydstyrken når lydintensiteten dobles?
<math>L_2 = 10log(2I) + 120 </math>
<math>L_2= 10log2+ 10logI + 120 </math>
<math>L_2 = 3 +(10logI + 120) </math>
<math>L_2 = 3 + L </math>
Når man dobler intensiteten øker lydstyrken med 3dB.
Som man ser fra eksemplene over er det mer praktisk å arbeide i dB, framfor å skulle arbeide direkte med lyditensitet.
Richters skala
Jordskjelv forårsakes av spenninger i jordskorpa. Sentrum av et jordskjelv kalles et episenter. Et jordskjelv friggjør energi i form av bølgebevegelser, som kan forårsake store materielle skader. Dersom episenteret er i eller ved vann kan det forårsake en stor flodbølger som kalles for en tsunami.
En av forskerne som arbeidet med matematiske modeller for å angi størrelsen på et jordskjelv var Dr. Charles F. Richter. Hen var Amerikaner og levde fra 1900 til 1985. I 1935 kom han med en modell som sier noe om styrken til et jordskjelv.:
<math> E = 10^{1,44R - 1,32} </math>
Der E er skjelvets energi målt i kWh og R er Richtertallet. Et jordskjelv som er 5 eller lavere på Richter skala er svakt og vil normalt ikke gi materielle skader. Jordskjelv over 6 på Richters skala er sterke. Skjelv over 8 vil normalt være katastrofale for store områder, flere hundre kilometer fra episentret. De største skjelv mann kjenner tilsvarer ca. 10 på Richters skala. Til sammenligning tilsvarer den daglige energimengden jorden mottar fra solen ca. 12 på Richters skala.
Hvor mye energi er utløst dersom et jordskjelv måler 7,9 på Richterskala?
<math> E = 10^{1,44 \cdot 7,9 - 1,32} = 10^{10,056}= 1,13 \cdot 10^{10} kWh</math>
Et jordskjelv utløser en energimengde på <math>5 \cdot 10^6 kWh</math>. Hvor stort er det på Richterskala?
<math>5 \cdot 10^6 = 10^{1,44R - 1,32}</math>
<math>1,44R - 1,32 = log(5 \cdot 10^6)</math>
<math>R = 5,6 </math>