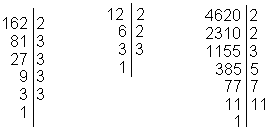Faktorisering, Delelighet, Fellesnevner: Forskjell mellom sideversjoner
| (33 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 17: | Linje 17: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<br>16 faktorisert skrives slik:<p></p> | '''Eksempel 1:'''<br>16 faktorisert skrives slik:<p></p> | ||
[[Bilde:Fak1.png]] | [[Bilde:Fak1.png]] | ||
| Linje 34: | Linje 34: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:'''<br> | '''Eksempel 2:'''<br> | ||
Vi faktoriserer tallene 162, 12 og 4620. | Vi faktoriserer tallene 162, 12 og 4620. | ||
<p></p> | <p></p> | ||
| Linje 50: | Linje 50: | ||
$4620 = 2 \cdot 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 $ | $4620 = 2 \cdot 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 $ | ||
</div> | </div> | ||
== Delelighet == | == Delelighet == | ||
| Linje 65: | Linje 56: | ||
'''Delelig med 2:''' <p></p> | '''Delelig med 2:''' <p></p> | ||
Et tall er delelig med to når siste siffer i tallet er delelig med to eller når det slutter på null. | Et tall er delelig med to når siste siffer i tallet er delelig med to eller når det slutter på null. | ||
</div> | </div> | ||
| Linje 73: | Linje 65: | ||
'''Eksempel:''' <p></p> | '''Eksempel 3:''' <p></p> | ||
24 er delelig med 2 fordi siste siffer, 4, er delelig med 2. 10 er delelig med to fordi det slutter med 0.</div> | 24 er delelig med 2 fordi siste siffer, 4, er delelig med 2. 10 er delelig med to fordi det slutter med 0.</div> | ||
| Linje 81: | Linje 75: | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Delelig med 3:'''<p></p> Dersom tallets tverrsum er delelig med tre er tallet delelig med tre.</div> | '''Delelig med 3:''' | ||
<p></p> Dersom tallets tverrsum er delelig med tre er tallet delelig med tre.</div> | |||
| Linje 87: | Linje 83: | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' <p></p> | '''Eksempel 4:''' <p></p> | ||
36 er delelig med 3 fordi tverrsummen av 36 er 3 + 6= 9 og 9 er delelig med 3.</ | |||
36 er delelig med 3 fordi tverrsummen av 36 er 3 + 6= 9 og 9 er delelig med 3.</div> | |||
< | <div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | ||
'''Delelig med 5:'''<p></p> | '''Delelig med 5:'''<p></p> | ||
Tall som ender på 0 og 5 er delelige med 5. | Tall som ender på 0 og 5 er delelige med 5. | ||
</ | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' <p></p> | '''Eksempel 5:''' <p></p> | ||
65 er delelig med 5 fordi det siste siffer i tallet er 5. | 65 er delelig med 5 fordi det siste siffer i tallet er 5. | ||
</div> | </div> | ||
<div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |||
:[https://youtu.be/E154zzHQ1VQ Video eksempel] | |||
</div> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=B1B%2BB1C%2BB20%2BB1E%2BB1F%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | [http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=B1B%2BB1C%2BB20%2BB1E%2BB1F%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | ||
| Linje 106: | Linje 115: | ||
== Fellesnevner == | == Fellesnevner == | ||
Når vi skal finne fellesnevner må vi først faktorisere alle nevnerne. Vi bruker metoden | Når vi skal finne fellesnevner må vi først faktorisere alle nevnerne. Vi bruker metoden i eksempel 1 og 2: | ||
< | <div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | ||
'''Eksempel:''' <p></p> | '''Eksempel 6:''' <p></p> | ||
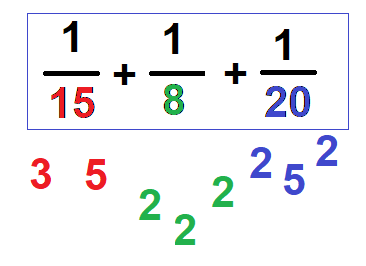
Vi har nevnerne 15, 8 og 20. Disse faktoriseres som vist i eksemplet over. Fellesnevneren må inneholde alle faktorene av 15, 8 og 20. | Vi har nevnerne 15, 8 og 20. Disse faktoriseres som vist i eksemplet over. Fellesnevneren må inneholde alle faktorene av 15, 8 og 20. | ||
| Linje 116: | Linje 125: | ||
"den som har flest vinner". | "den som har flest vinner". | ||
[[Bilde: | |||
[[Bilde:Skjermbilde 2023-03-09 114922.png ]] | |||
Vi begynner med de laveste tallet som er to. Åtte faktorisert gir tre (grønne) toere, altså skal disse med i fellesnevner. Når vi faktoriserer 15 får vi 3 og 5 (rød). Vi har ikke disse med i fellesnevnere fra før, så disse må være med. Fellesnevneren ser da slik ut: | |||
Det betyr at vi trenger tre 2 -ere i fellesnevner. Neste tall er 3, som det bare er en av. Vi ser at det er to 5 -ere, en fra 15 og en fra 20. Vi tar med en 5 -er. | Det betyr at vi trenger tre 2 -ere i fellesnevner. Neste tall er 3, som det bare er en av. Vi ser at det er to 5 -ere, en fra 15 og en fra 20. Vi tar med en 5 -er. | ||
| Linje 125: | Linje 138: | ||
Figuren viser at fellesnevner inkluderer alle faktorene som forekommer i hver av de faktoriserte nevnerne. | Figuren viser at fellesnevner inkluderer alle faktorene som forekommer i hver av de faktoriserte nevnerne. | ||
</ | </div> | ||
| Linje 132: | Linje 145: | ||
De faktorene som er med i fellesnevner og ikke i brøkens nevner, er de faktorene brøken må utvides med for at man oppnår å få fellesnevner i brøken. (se [[Brøkregning]] ). | De faktorene som er med i fellesnevner og ikke i brøkens nevner, er de faktorene brøken må utvides med for at man oppnår å få fellesnevner i brøken. (se [[Brøkregning]] ). | ||
<div style="padding: 1em; border: 1px blue; background-color: #FFFF66 ;"> | |||
:[https://youtu.be/Zj9-qbqDUIc Video eksempel] | |||
</div> | |||
== MFM == | == MFM == | ||
Minste felles multiplum skrives ofte MFM. Dersom vi skal finne minste felles multiplum av 12 og 18 starter vi med å faktorisere begge tallene: 12 = 2·2·3 og 18 = 2·3·3. I dette tilfellet blir MFM = 2·2·3·3 = 36, fordi 36 er det minste tallet både 12 og 18 går opp i, altså deres minste felles multiplum. | '''Minste felles multiplum''' skrives ofte MFM. Dersom vi skal finne minste felles multiplum av 12 og 18 starter vi med å faktorisere begge tallene: 12 = 2·2·3 og 18 = 2·3·3. I dette tilfellet blir MFM = 2·2·3·3 = 36, fordi 36 er det minste tallet både 12 og 18 går opp i, altså deres minste felles multiplum. | ||
Vi skriver det slik: | Vi skriver det slik: | ||
| Linje 145: | Linje 163: | ||
== SFD == | == SFD == | ||
Det største tallet som går opp i både 12 og 18 er 6. Vi sier at 6 er største felles divisor, sfd, eller største felles mål. | Det største tallet som går opp i både 12 og 18 er 6. Vi sier at 6 er '''største felles divisor''', sfd, eller største felles mål. | ||
Vi skriver det slik: | Vi skriver det slik: | ||
| Linje 152: | Linje 170: | ||
Sammenhengen mellom minste felles multiplum og største felles divisor er: | Sammenhengen mellom minste felles multiplum og største felles divisor er: | ||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
a·b = mfm (a ,b)· sfd (a, b) | a·b = mfm (a ,b)· sfd (a, b) | ||
</div> | |||
<div style="padding: 1em; border: 1px blue; background-color: #F8ADB6;"> | |||
'''Eksempel 7:''' | |||
Produktet av 16 og 24 er $16 \cdot 24= 384$ | |||
$16= 2 \cdot 2 \cdot 2 \cdot 2$ | |||
$24= 2 \cdot 2 \cdot 2 \cdot 3$ | |||
$MFM(16, 24)= 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 48$ | |||
$SFD(16, 24) = 2 \cdot 2 \cdot 2 = 8$ | |||
Vi observerer at | |||
$MFM(16, 24) \cdot SFD(16,24) = 48 \cdot 8 = 384$ som jo er produktet av 16 og 24. | |||
</div> | |||
==Faktorisering av ledd== | |||
$4x^2-8x = 4x(x-2)$ | |||
Uttrykket består av to ledd på venstre side. Ledd er uttrykk som adskilles av pluss eller minus. I eksempelet er $4x^2$ og $8x$ to ledd. På høyresiden har man tre faktorer, 4, x og (x-2). Faktorer er del av et produkt. | |||
Når du har klart for deg hva et ledd er og hvor mange ledd det er i utrykket, ser du etter felles faktorer i leddene, og setter det / dem utenfor en parentes. Det som står igjen inni parentesen er den faktoren du må gange det som står på utsiden av parentesen med, for å komme tilbake til uttrykket som var utgangspunktet. | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=B16%2BB17%2BB18%2BB19%2BB1A%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
Siste sideversjon per 11. mar. 2023 kl. 13:51
Faktorisering av tall
Faktorisering er ofte brukt i matematikken. Det går ut på å skrive et tall som produktet av faktorer. Tallet 4 kan skrives som 2 · 2. Dersom vi skriver 4 som 2 ·2 har vi faktorisert 4. Dette bruker vi ofte når vi skal finne fellesnevner eller forkorte.
Dersom vi skriver 8 = 2 · 4 har vi faktorisert 8. Men, vi har ikke primtallsfaktorisert siden 4 ikke er et primtall. Dersom vi skriver 8 = 2 · 2 · 2 har vi primtallsfaktorisert 8.
Gjør følgende:
Skriv tallet som skal faktoriseres på venstre side av en lang loddrett strek. Begynn med å prøve å dele tallet på 2. Dersom det er mulig skriver du 2 på høyre side av streken og svaret du får under tallet på venstre side av streken. Når du ikke kan dele på 2 lenger prøver vi med 3. Slik fortsetter vi med 5, 7 osv. Dersom man multiplisere alle primtallene på høyre side av streken skal man få det tallet man startet med.
16 faktorisert skrives slik:
Vi delte på to fire ganger. Dersom vi multipliserer divisorene ender vi opp med det tallet vi startet med.
2 ·2 · 2 · 2 =16
16 på faktorisert form skrives altså som 2 · 2 · 2 · 2.
Eksempel 2:
Vi faktoriserer tallene 162, 12 og 4620.
Vi begynner med å dele på 2. Når det ikke går lenger prøver vi med det neste primtallet.
$162= 2 \cdot 3 \cdot 3 \cdot 3 \cdot 3 $
$12= 2 \cdot 2 \cdot 3 $
$4620 = 2 \cdot 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 $
Delelighet
Et tall er delelig med to når siste siffer i tallet er delelig med to eller når det slutter på null.
Delelig med 3:
Dersom tallets tverrsum er delelig med tre er tallet delelig med tre.
Tall som ender på 0 og 5 er delelige med 5.
65 er delelig med 5 fordi det siste siffer i tallet er 5.
Fellesnevner
Når vi skal finne fellesnevner må vi først faktorisere alle nevnerne. Vi bruker metoden i eksempel 1 og 2:
Vi har nevnerne 15, 8 og 20. Disse faktoriseres som vist i eksemplet over. Fellesnevneren må inneholde alle faktorene av 15, 8 og 20.
Vi begynner med den minste faktoren, 2. Den forekommer tre ganger i 8 og to ganger i 20. Vi har følgende regel:
"den som har flest vinner".
Vi begynner med de laveste tallet som er to. Åtte faktorisert gir tre (grønne) toere, altså skal disse med i fellesnevner. Når vi faktoriserer 15 får vi 3 og 5 (rød). Vi har ikke disse med i fellesnevnere fra før, så disse må være med. Fellesnevneren ser da slik ut:
Det betyr at vi trenger tre 2 -ere i fellesnevner. Neste tall er 3, som det bare er en av. Vi ser at det er to 5 -ere, en fra 15 og en fra 20. Vi tar med en 5 -er.
Fellesnevner, som også kalles minste felles multiplum, er:
FN = 2 · 2 · 2 · 3 · 5 = 120
Figuren viser at fellesnevner inkluderer alle faktorene som forekommer i hver av de faktoriserte nevnerne.
De faktorene som er med i fellesnevner og ikke i brøkens nevner, er de faktorene brøken må utvides med for at man oppnår å få fellesnevner i brøken. (se Brøkregning ).
MFM
Minste felles multiplum skrives ofte MFM. Dersom vi skal finne minste felles multiplum av 12 og 18 starter vi med å faktorisere begge tallene: 12 = 2·2·3 og 18 = 2·3·3. I dette tilfellet blir MFM = 2·2·3·3 = 36, fordi 36 er det minste tallet både 12 og 18 går opp i, altså deres minste felles multiplum.
Vi skriver det slik:
mfm(12, 18) = 36
Dette finne vi ved å samle primtallsfaktorene fra 2 og oppover, der flest antall "like" er tellende; vi samler 2-er faktorene fra 12 fordi 12 har to 2-er faktorer mens 18 bare har en. Treerfaktorene kommer fra 18 fordi 18 har to 3-er faktorer mot 12's ene.
SFD
Det største tallet som går opp i både 12 og 18 er 6. Vi sier at 6 er største felles divisor, sfd, eller største felles mål.
Vi skriver det slik:
sfd ( 12, 18) = 6
Sammenhengen mellom minste felles multiplum og største felles divisor er:
a·b = mfm (a ,b)· sfd (a, b)
Eksempel 7:
Produktet av 16 og 24 er $16 \cdot 24= 384$
$16= 2 \cdot 2 \cdot 2 \cdot 2$
$24= 2 \cdot 2 \cdot 2 \cdot 3$
$MFM(16, 24)= 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 48$
$SFD(16, 24) = 2 \cdot 2 \cdot 2 = 8$
Vi observerer at
$MFM(16, 24) \cdot SFD(16,24) = 48 \cdot 8 = 384$ som jo er produktet av 16 og 24.
Faktorisering av ledd
$4x^2-8x = 4x(x-2)$
Uttrykket består av to ledd på venstre side. Ledd er uttrykk som adskilles av pluss eller minus. I eksempelet er $4x^2$ og $8x$ to ledd. På høyresiden har man tre faktorer, 4, x og (x-2). Faktorer er del av et produkt.
Når du har klart for deg hva et ledd er og hvor mange ledd det er i utrykket, ser du etter felles faktorer i leddene, og setter det / dem utenfor en parentes. Det som står igjen inni parentesen er den faktoren du må gange det som står på utsiden av parentesen med, for å komme tilbake til uttrykket som var utgangspunktet.