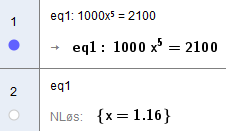2P 2021 vår LØSNING: Forskjell mellom sideversjoner
mIngen redigeringsforklaring |
|||
| (46 mellomliggende versjoner av en annen bruker er ikke vist) | |||
| Linje 7: | Linje 7: | ||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHWOQ70eqozJojw-jW_B8pF5 Videoløsninger til del 1 laget av Lektor Håkon Raustøl] | [https://www.youtube.com/playlist?list=PLplkS_rtcCHWOQ70eqozJojw-jW_B8pF5 Videoløsninger til del 1 laget av Lektor Håkon Raustøl] | ||
[https://youtu.be/ojJdNxyKWns Videoløsning del 1 av lektor lainz] | |||
==DEL 1== | ==DEL 1== | ||
| Linje 94: | Linje 94: | ||
===a)=== | ===a)=== | ||
Dersom en størrelse forandrer seg med en gitt prosent hver eneste tidsperiode har man en situasjon med eksponentiell vekst. | Dersom en størrelse forandrer seg med en gitt prosent hver eneste tidsperiode har man en situasjon med eksponentiell vekst. Bakterier kan vokse tilnærmet eksponentielt. | ||
===b)=== | |||
I en bakteriekultur er det 50 000 bakterier. Kulturen vokser med 5% per time. Hvor lang tid tar det før man har 1 000 000 bakterier? | |||
Kan løses på mange måter. Grafisk: tegn $f(x) = 50 000 \cdot 1,05^x$ og y= 1 000 000 i samme koordinatsystem og finn skjæring. | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 111: | Linje 114: | ||
===c)=== | ===c)=== | ||
Pinner: $P(n)= n + (n-1) = 2n-1$. | |||
Kuler: $ K(n)= n \cdot (n-1) = n^2-n$ | |||
==DEL 2== | ==DEL 2== | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
[[File:24022022-5.png]] | |||
Ved å velge potensregresjon får man funksjonen S (x). | |||
===b)=== | |||
I 2011, tre år etter 2008 var bestanden ca.7.686.000 tonn. | |||
===c)=== | |||
Modellen passer dårlig i forhold til prognosen havforskningsinstituttet har. Olavs "modell" flater ut. Den kan gi en omtrentlig beskrivelse av historien, men er ikke en modell som er egnet til å si noe om framtiden. | |||
==Oppgave 2== | ==Oppgave 2== | ||
===a)=== | |||
[[File: 24022022-61.png]] | |||
===b)=== | |||
I perioden 2007 til 2017 var produksjonen lavere enn 84 000 tonn. | |||
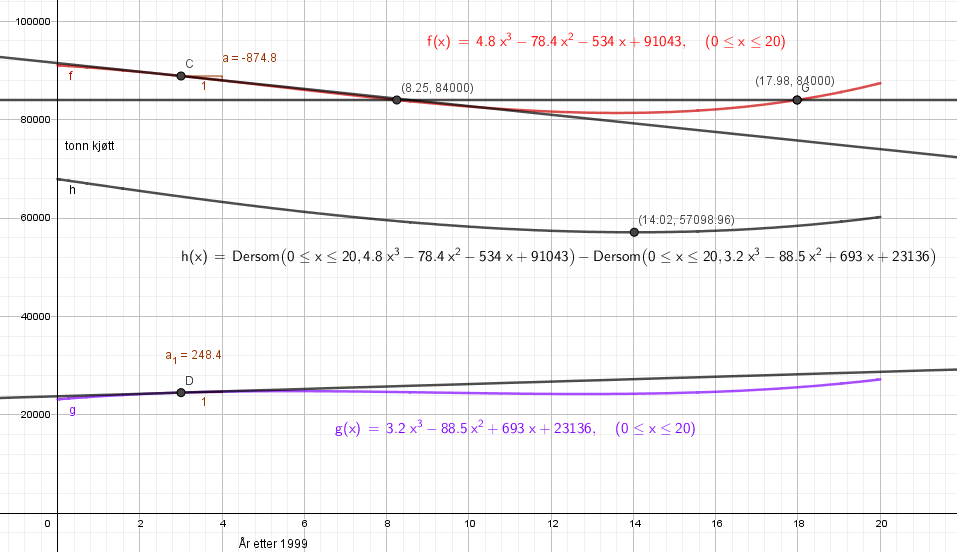
===c)=== | |||
Den momentane veksten uttrykker endringen i øyeblikket og i 2002 var produksjon av storfekjøtt ned med 875 tonn og produksjon sauekjøtt økte med 248 tonn. | |||
===d)=== | |||
Bunnpunktet på h er i 2013. Da er forskjellen mellom produksjon av storfekjøtt og sauekjøtt på sitt laveste, 57099 tonn. | |||
==Oppgave 3== | ==Oppgave 3== | ||
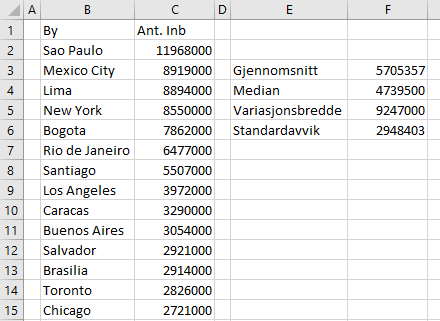
===a)=== | |||
[[File: 25022022-6.png]] [[File: 25022022-7.png]] | |||
===b)=== | |||
Byene i Europa er gjennomgående mindre, men en eller 2-3 er med på å dra opp gjennomsnittet. Vi ser at medianverdi i Europa er betydelig lavere enn i Amerika. Begge spredningsmålene, variasjonsbredde og standardavvik er større i Europa. Det betyr større spredning i størrelse, og sammen med forskjellen på median og gjennomsnitt støtter det opp om at Europa har ca. 1-3 byer som drar opp snittet betydelig. | |||
===c)=== | |||
I de fjorten største byene i Europa bor det $14 \cdot 4808000 = 67 312000$ personer. Trekker man fra Itanbul blir antallet 51.793.000 og deler man det på 13 får man ett gjennomsnitt på 3.984.077 personer. | |||
==Oppgave 4== | ==Oppgave 4== | ||
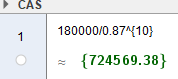
===a)=== | |||
Bruker vekstfaktor: | |||
[[File: 25022022-2.png]] | |||
Den var verdt ca 725 000 kroner. | |||
===b)=== | |||
[[File:25022022-1.png]] | |||
Den synker med ca. 11% per år. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
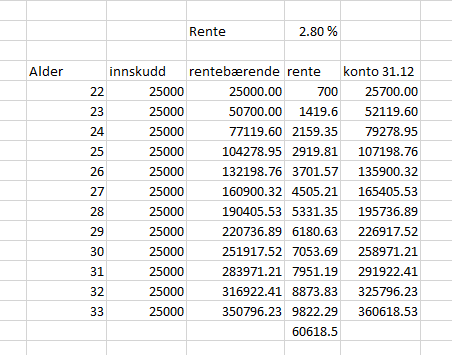
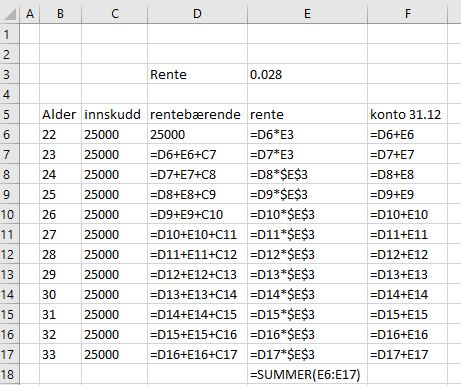
[[File:02032022-01.png ]] [[File:02032022-02.png ]] | |||
===b)=== | |||
60618,50 kroner. | |||
==Oppgave 6== | ==Oppgave 6== | ||
Situasjon 1 beskrives av graf A, x aksen er kilogram jordbær og y aksen er lønn. | |||
Situasjon 2 beskrives av graf B, selv om den siste grafen trolig burde startet noe høyere pga. akkumulert virkestoff. x aksen viser tre døgn. | |||
Situasjon 3 beskrives av graf D. | |||
Situasjon 4 beskrives av graf F, når de fleste kjenner til ryktet flater kurven ut. Samme type kurve som bæreevnen i en populasjon. | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
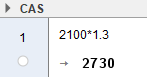
[[File:25022022-3.png]] | |||
I September fikk de 2730 henvendelser. | |||
===b)=== | |||
$\frac{400}{3600}= 0,11$ som tilsvarer en nedgang på 11%. | |||
===c)=== | |||
Først finner vi vekstfaktoren så vi kan bestemme den prosentvise veksten: Det er fem perioder: | |||
[[File:25022022-4.png]] | |||
Veksten er på ca 16%, vekstfaktor 1,16. Summen av henvendelser blir: | |||
[[File:25022022-5.png]] | |||
Altså rett i underkant av 9000 henvendelser. | |||
Siste sideversjon per 15. mai 2022 kl. 18:52
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Videoløsninger til del 1 laget av Lektor Håkon Raustøl
Videoløsning del 1 av lektor lainz
DEL 1
Oppgave 1
0,0,0,0, 4, 13, 15,17,20,26
Median er (4+13)/2 = 8,5.
Typetall er 0.
Gjennomsnitt er 95/10 = 9,5
Variasjonsbredde er 26 - 0 = 26.
Oppgave 2
Vi gjør alt om til standardform:
250 millioner = $2,5\cdot 10^8$
$0,25 \cdot 10^{10} = 2,5 \cdot 10^9$
$2500\cdot 10^7 = 2,5 \cdot 10^{10}$
$0,250 \cdot 10^{-5} = 2,5 \cdot 10^{-6}$
$0,025 \cdot 10^{-2} = 2,5 \cdot 10^{-4}$
$0,0025\% = \frac{0,0025}{100} = 0,000025 = 2,5 \cdot 10^{-5}$
Da er det bare å ta utgangspunkt i eksponentene for å få stigende rekkefølge.
$0,250 \cdot 10^{-5} = 2,5 \cdot 10^{-6}$
$0,0025\% = \frac{0,0025}{100} = 0,000025 = 2,5 \cdot 10^{-5}$
$0,025 \cdot 10^{-2} = 2,5 \cdot 10^{-4}$
250 millioner = $2,5\cdot 10^8$
$0,25 \cdot 10^{10} = 2,5 \cdot 10^9$
$2500\cdot 10^7 = 2,5 \cdot 10^{10}$
Oppgave 3
$(x \cdot 0,9)\cdot 0,8 = 720$
$0,72 x = 720$
$x= \frac{720}{0,72} = 1000$
Varen kostet 1000 kroner før første nedsettelse.
Oppgave 4
a)
$P(x)= \frac{3000}{x} +100$
b)
$P(x)=130$
$130 = \frac{3000}{x} + 100$
$130x - 100x = 3000$
x =100
For at prisen skal bli lavere enn 130 kroner, må minst 101 personer komme på avslutningen.
Oppgave 5
a)
b)
Oppgave 6
a)
Dersom en størrelse forandrer seg med en gitt prosent hver eneste tidsperiode har man en situasjon med eksponentiell vekst. Bakterier kan vokse tilnærmet eksponentielt.
b)
I en bakteriekultur er det 50 000 bakterier. Kulturen vokser med 5% per time. Hvor lang tid tar det før man har 1 000 000 bakterier?
Kan løses på mange måter. Grafisk: tegn $f(x) = 50 000 \cdot 1,05^x$ og y= 1 000 000 i samme koordinatsystem og finn skjæring.
Oppgave 7
a)
b)
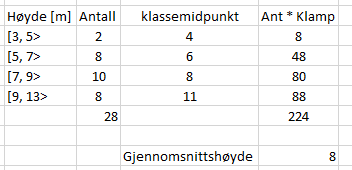
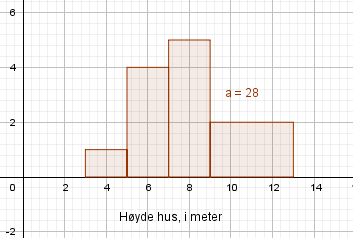
I figur 10 vil det vøre 10 + 9 pinner, altså 19. Det vil være 10 ganger 9 kuler, altså 90.
c)
Pinner: $P(n)= n + (n-1) = 2n-1$.
Kuler: $ K(n)= n \cdot (n-1) = n^2-n$
DEL 2
Oppgave 1
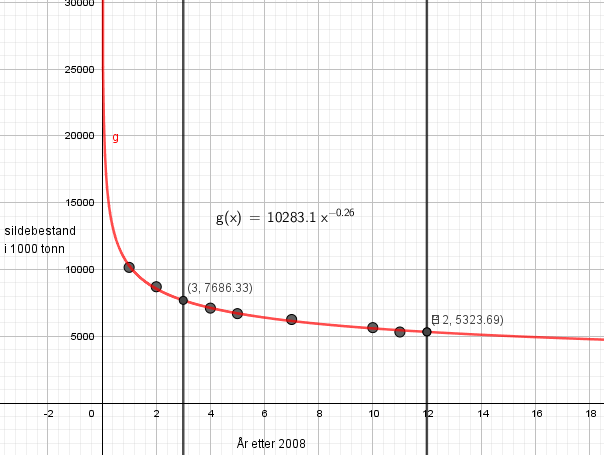
a)
Ved å velge potensregresjon får man funksjonen S (x).
b)
I 2011, tre år etter 2008 var bestanden ca.7.686.000 tonn.
c)
Modellen passer dårlig i forhold til prognosen havforskningsinstituttet har. Olavs "modell" flater ut. Den kan gi en omtrentlig beskrivelse av historien, men er ikke en modell som er egnet til å si noe om framtiden.
Oppgave 2
a)
b)
I perioden 2007 til 2017 var produksjonen lavere enn 84 000 tonn.
c)
Den momentane veksten uttrykker endringen i øyeblikket og i 2002 var produksjon av storfekjøtt ned med 875 tonn og produksjon sauekjøtt økte med 248 tonn.
d)
Bunnpunktet på h er i 2013. Da er forskjellen mellom produksjon av storfekjøtt og sauekjøtt på sitt laveste, 57099 tonn.
Oppgave 3
a)
b)
Byene i Europa er gjennomgående mindre, men en eller 2-3 er med på å dra opp gjennomsnittet. Vi ser at medianverdi i Europa er betydelig lavere enn i Amerika. Begge spredningsmålene, variasjonsbredde og standardavvik er større i Europa. Det betyr større spredning i størrelse, og sammen med forskjellen på median og gjennomsnitt støtter det opp om at Europa har ca. 1-3 byer som drar opp snittet betydelig.
c)
I de fjorten største byene i Europa bor det $14 \cdot 4808000 = 67 312000$ personer. Trekker man fra Itanbul blir antallet 51.793.000 og deler man det på 13 får man ett gjennomsnitt på 3.984.077 personer.
Oppgave 4
a)
Bruker vekstfaktor:
Den var verdt ca 725 000 kroner.
b)
Den synker med ca. 11% per år.
Oppgave 5
a)
b)
60618,50 kroner.
Oppgave 6
Situasjon 1 beskrives av graf A, x aksen er kilogram jordbær og y aksen er lønn.
Situasjon 2 beskrives av graf B, selv om den siste grafen trolig burde startet noe høyere pga. akkumulert virkestoff. x aksen viser tre døgn.
Situasjon 3 beskrives av graf D.
Situasjon 4 beskrives av graf F, når de fleste kjenner til ryktet flater kurven ut. Samme type kurve som bæreevnen i en populasjon.
Oppgave 7
a)
I September fikk de 2730 henvendelser.
b)
$\frac{400}{3600}= 0,11$ som tilsvarer en nedgang på 11%.
c)
Først finner vi vekstfaktoren så vi kan bestemme den prosentvise veksten: Det er fem perioder:
Veksten er på ca 16%, vekstfaktor 1,16. Summen av henvendelser blir:
Altså rett i underkant av 9000 henvendelser.