Tall: Forskjell mellom sideversjoner
Ny side: 2.5. Naturlige tall De naturlige tallene er: 1,2,3,4,5,6,7......... Vi kaller denne tallmengden for N. 2.6. Partall Partallene er 2,4,6,8,10,12…………. Partall er delelig på to.... |
m 0 er også et naturlig tall. |
||
| (27 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
== Naturlige tall, - $\mathbb{N}$== | |||
De naturlige tallene er: 1,2,3,4,5,6,7......... Vi kaller denne tallmengden for N. | De naturlige tallene er: 0, 1, 2, 3, 4, 5, 6, 7, ............Vi kaller denne tallmengden for $\mathbb{N}$. | ||
=== Partall === | |||
2. | Partallene er 2, 4, 6, 8....2n, der n er et naturlig tall forskjellig fra null. | ||
=== Oddetall === | |||
Oddetallene er 1,3,5,7,9,11…….. Oddetallene er ikke delelige på to. Oddetall er en del av de naturlige tallene. | Oddetallene er 1,3,5,7,9,11…….. Oddetallene er ikke delelige på to. Oddetall er en del av de naturlige tallene. | ||
Dersom du lurer på om et tall kan deles på et annet kan du se på | Dersom du lurer på om et tall kan deles på et annet kan du se på [[Faktorisering, Delelighet, Fellesnevner#Delelighet|Delelighet]]. | ||
=== Primtall === | |||
Primtall er naturlige tall som kun er delelige på seg selv og en. Legg merke till at 1 ikke er et primtall. | Primtall er naturlige tall som kun er delelige på seg selv og en. Legg merke till at 1 ikke er et primtall. | ||
| Linje 23: | Linje 28: | ||
Primtall er en del av de naturlige tallene. | Primtall er en del av de naturlige tallene. | ||
== Hele tall, - $\mathbb{Z}$ == | |||
Dersom vi tar alle de naturlige tallene inkluderer de hele negative tallene får vi en tallmengde vi kaller for Z, som er de hele tallene. | Dersom vi tar alle de naturlige tallene inkluderer de hele negative tallene får vi en tallmengde vi kaller for $\mathbb{Z}$, som er de hele tallene. | ||
Z : ....., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,....... | Z : ....., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,....... | ||
== Rasjonale tall, - $\mathbb{Q}$ == | |||
En brøk er det vi kaller et rasjonalt tall. Et rasjonalt tall kan skrives som a/b. Alle rasjonale tall har enten en avsluttende desimal (teller delt på nevner har rest null etter et gitt antall desimaler), eller en periodisk desimalutvikling. | En brøk er det vi kaller et rasjonalt tall. Et rasjonalt tall kan skrives som a/b. Alle rasjonale tall har enten en avsluttende desimal (teller delt på nevner har rest null etter et gitt antall desimaler), eller en periodisk desimalutvikling. | ||
| Linje 39: | Linje 46: | ||
4/11 kan skrives som 0,363636363636363636........ | 4/11 kan skrives som 0,363636363636363636........ | ||
Det første eksempelet har en avsluttende desimal. Vi ser at i de to siste eksemplene | Det første eksempelet har en avsluttende desimal. Vi ser at i de to siste eksemplene gjentas sifrene i det uendelige. I tallet 0,666666... kan vi si at perioden er 6. I tallet 0,36363636 er perioden 36. Alle desimaltall som har en periode er rasjonale tall. Vi kaller de rasjonale tallene for $\mathbb{Q}$ . | ||
== Reelle tall, - $\mathbb{R}$ == | |||
Det finnes enkelte tall som ikke kan skrives som brøk. Et eksempel på det er tallet π (pi). Dersom du prøver å trykke det symbolet på kalkulatoren får du 3,141592654...... Det er ingen periode her, som det er i de rasjonale tallene. Vi kaller denne type tall for et irrasjonalt tall. De rasjonale og de irrasjonale tallene danner den tallmengden som vi kaller for de reelle tallene. Vi bruker symbolet $\mathbb{R}$ . $\mathbb{R}$ inneholder alle tallene på tallinja. | |||
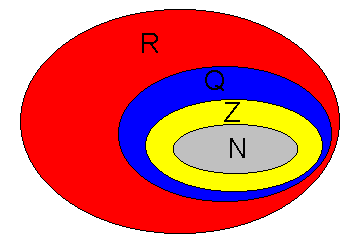
[[Image:mengder.gif]] | |||
''Figuren viser tallmengdene på tallinja. Legg merke til at $\mathbb{N}$ er en delmengde av $\mathbb{Z}$ og $\mathbb{Z}$ er igjen en delmengde av $\mathbb{Q}$ osv.'' | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=AC0%2BAC1%2BAC2%2BAC3%2BAC4%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
---- | |||
[[Ungdomstrinn Hovedside | Tilbake til Ungdomstrinn Hovedside]]<p></p> | |||
[[Hovedside| Tilbake til hovedside]] | |||
[[Category:Geometri]] | |||
[[Category:U - trinn]] [[Category:Ped]] | |||
[[Kategori:1T]] | [[Kategori:1T]] | ||
[[Kategori:Logikk og mengdelære]] | |||
Siste sideversjon per 3. sep. 2021 kl. 08:17
Naturlige tall, - $\mathbb{N}$
De naturlige tallene er: 0, 1, 2, 3, 4, 5, 6, 7, ............Vi kaller denne tallmengden for $\mathbb{N}$.
Partall
Partallene er 2, 4, 6, 8....2n, der n er et naturlig tall forskjellig fra null.
Oddetall
Oddetallene er 1,3,5,7,9,11…….. Oddetallene er ikke delelige på to. Oddetall er en del av de naturlige tallene.
Dersom du lurer på om et tall kan deles på et annet kan du se på Delelighet.
Primtall
Primtall er naturlige tall som kun er delelige på seg selv og en. Legg merke till at 1 ikke er et primtall.
De minste primtallene er: 2,3,5,7,11,13,...................
Et naturlig tall som ikke er et primtall kaller vi et sammensatt tall. Sammensatte tall kan faktoriseres.
Primtall er en del av de naturlige tallene.
Hele tall, - $\mathbb{Z}$
Dersom vi tar alle de naturlige tallene inkluderer de hele negative tallene får vi en tallmengde vi kaller for $\mathbb{Z}$, som er de hele tallene.
Z : ....., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4,.......
Rasjonale tall, - $\mathbb{Q}$
En brøk er det vi kaller et rasjonalt tall. Et rasjonalt tall kan skrives som a/b. Alle rasjonale tall har enten en avsluttende desimal (teller delt på nevner har rest null etter et gitt antall desimaler), eller en periodisk desimalutvikling.
1/5 kan skrives som 0,2
2/3 kan skrives som 0,666666666666...........
4/11 kan skrives som 0,363636363636363636........
Det første eksempelet har en avsluttende desimal. Vi ser at i de to siste eksemplene gjentas sifrene i det uendelige. I tallet 0,666666... kan vi si at perioden er 6. I tallet 0,36363636 er perioden 36. Alle desimaltall som har en periode er rasjonale tall. Vi kaller de rasjonale tallene for $\mathbb{Q}$ .
Reelle tall, - $\mathbb{R}$
Det finnes enkelte tall som ikke kan skrives som brøk. Et eksempel på det er tallet π (pi). Dersom du prøver å trykke det symbolet på kalkulatoren får du 3,141592654...... Det er ingen periode her, som det er i de rasjonale tallene. Vi kaller denne type tall for et irrasjonalt tall. De rasjonale og de irrasjonale tallene danner den tallmengden som vi kaller for de reelle tallene. Vi bruker symbolet $\mathbb{R}$ . $\mathbb{R}$ inneholder alle tallene på tallinja.
Figuren viser tallmengdene på tallinja. Legg merke til at $\mathbb{N}$ er en delmengde av $\mathbb{Z}$ og $\mathbb{Z}$ er igjen en delmengde av $\mathbb{Q}$ osv.