2P 2020 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (59 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 6: | Linje 6: | ||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=51505&start=30#p238346 Løsning del 2 laget av Kristian Saug] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=51505&start=30#p238346 Løsning del 2 laget av Kristian Saug] | ||
[https://youtu.be/nxAGObz6IUE Videoløsning del 1 av Lektor Lainz] | |||
[https://youtu.be/Ab8Da7zlO3I Videoløsning del 2 av Lektor Lainz] | |||
=DEL 1= | =DEL 1= | ||
| Linje 26: | Linje 30: | ||
===b)=== | ===b)=== | ||
{| width="auto" | {| width="auto" | ||
| Antall ganger en elev hjelper | | Antall ganger en elev hjelper | ||
| Linje 87: | Linje 92: | ||
Det er en prisforskjell på 60 kr mellom flybussen og bybanen, og flybussen koster 100 kr. | Det er en prisforskjell på 60 kr mellom flybussen og bybanen, og flybussen koster 100 kr. | ||
$\frac{60}{100}=60% | $\frac{60}{100}=60$% | ||
Bybanen er 60% billigere sammenlignet med flybussen. | Bybanen er 60% billigere sammenlignet med flybussen. | ||
| Linje 95: | Linje 100: | ||
Det er en prisforskjell på 60 kr mellom flybussen og bybanen, og bybanen koster 40 kr. | Det er en prisforskjell på 60 kr mellom flybussen og bybanen, og bybanen koster 40 kr. | ||
$\frac{60}{40}=\frac{3}{2}=1,5 = 150% | $\frac{60}{40}=\frac{3}{2}=1,5 = 150$% | ||
Flybussen er 150% dyrere sammenlignet med bybanen. | Flybussen er 150% dyrere sammenlignet med bybanen. | ||
==Oppgave 3== | ==Oppgave 3== | ||
Lineær vekst vil si at vi har en fast startverdi (konstantledd), og deretter en konstant vekst per enhet (et konstant stigningstall). Et eksempel er en drosjetur der hvor startprisen er 60 kr, og prisen per km er 16 kr. Vi kan da uttrykket prisen for turen, y, etter x km kjørt, ved $y=16x+60$ | |||
Eksponentiell vekst vil si at vi har en fast startverdi, og deretter en prosentvis økning per enhet. Et eksempel er en leilighet som koster 3.000.000 kr, og hvor prisen går opp med 1,5% per år. Vi kan da uttrykke prisen på leiligheten, f(x), etter x år ved $f(x)=3000000\cdot 1,015^x$ | |||
==Oppgave 4== | |||
Gjør om tonn til gram: $45$ tonn $= 45 000 000$ g | |||
Regner ut antall hengelåser: $\frac{45 000 000}{50}=900 000 = 9\cdot 10^5$ | |||
Det var omtrent $ 9\cdot 10^5$ hengelåser på rekkverket. | |||
==Oppgave 5== | |||
===a)=== | |||
{| width="auto" | |||
|Poeng | |||
|Klassemidtpunkt, m | |||
|Antall elever, a | |||
|$m\cdot a$ | |||
|- | |||
| $[ \, 0,10 \rangle$ | |||
| 5 | |||
| 4 | |||
| 20 | |||
|- | |||
| $[ \, 10,20 \rangle$ | |||
|15 | |||
|12 | |||
|180 | |||
|- | |||
|$[ \, 20,30 \rangle$ | |||
|25 | |||
|34 | |||
|850 | |||
|- | |||
|$[ \, 30,40 \rangle$ | |||
|35 | |||
|30 | |||
|1050 | |||
|- | |||
|$[ \, 40,60 \rangle$ | |||
|50 | |||
|20 | |||
|1000 | |||
|- | |||
|Sum | |||
| | |||
|100 | |||
|3100 | |||
|} | |||
Gjennomsnitt: $\frac{3100}{100}=31$ | |||
Gjennomsnittlig antall poeng på kartleggingsprøven var 31. | |||
===b)=== | |||
Beregninger for å lage histogram: | |||
{| width="auto" | |||
|Poeng | |||
|Klassebredde | |||
|Antall elever (frekvens) | |||
|Frekvens / klassebredde | |||
|- | |||
| $[ \, 0,10 \rangle$ | |||
| 10 | |||
| 4 | |||
| 0,4 | |||
|- | |||
| $[ \, 10,20 \rangle$ | |||
|10 | |||
|12 | |||
|1,2 | |||
|- | |||
|$[ \, 20,30 \rangle$ | |||
|10 | |||
|34 | |||
|3,4 | |||
|- | |||
|$[ \, 30,40 \rangle$ | |||
|10 | |||
|30 | |||
|3 | |||
|- | |||
|$[ \, 40,60 \rangle$ | |||
|20 | |||
|20 | |||
|1 | |||
|} | |||
Histogram (som du må tegne for hånd): | |||
[[File: 2P_v20_5b.png]] | |||
==Oppgave 6== | |||
===a)=== | |||
$f(x)=200000\cdot 0,95^{10}$ | |||
===b)=== | |||
Dersom båtens verdi sank med 10 000 kr per år i 10 år, ville den hatt et totalt verditap på 100 000 kr, og være verdt 100 000 kr om 10 år. Men dette er ikke tilfellet, båtens verdi synker prosentvis hvert år, og båtens verditap blir derfor lavere og lavere for hvert år. | |||
Nærmere forklart: det første året minker verdien av båten med 5% av 200 000 kr, altså 10000 kr. Det andre året er verdien av båten 190 000 kr, og verdien av båten synker fremdeler med 5% hvert år. 5% av 190 000 kr er 9500 kr, det vil si at båtens verdi synker med mindre enn 10 000 kr det andre året. Båtens verdi blir lavere og lavere for hvert år, og 5% av verdien blir et lavere og lavere verditap for hvert år. Båtens verdi synker altså ikke med 10 000 kr hvert år, og det totale verditapet etter 10 år blir lavere enn 100 000 kr. Båten er verdt mer enn 100 000 kr etter 10 år. | |||
==Oppgave 7== | |||
===a)=== | |||
Jeg bruker tabell for å få en oversikt både til oppgave a) og b). | |||
{| width="auto" | |||
| | |||
|Figur 1 | |||
|Figur 2 | |||
|Figur 3 | |||
|Figur 10 | |||
|Figur n | |||
|- | |||
|Antall grønne kvadrater | |||
|$2\cdot 4=8$ | |||
|$3\cdot 4=12$ | |||
|$4\cdot 4=16$ | |||
|$11\cdot 4=44$ | |||
|$(n+1)\cdot 4$ | |||
|- | |||
|Antall hvite kvadrater | |||
|$1^2=1$ | |||
|$2^2=4$ | |||
|$3^3=9$ | |||
|$10^2=100$ | |||
|$n^2$ | |||
|} | |||
Det er 44 grønne kvadrater i figur 10, se utregning i tabellen. | |||
===b)=== | |||
Et uttrykk for antall grønne kvadrater når antall små hvite kvadrater er $n^2$: | |||
$(n+1)\cdot 4 \\= 4n+4$ | |||
Se tabellen i a) for tankegangen bak. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
Bruker Geogebra for å tegne grafene til M og T. | |||
[[File: 2P_v20_1a.png]] | |||
===b)=== | |||
Bruker "skjæringspunkt mellom to objekt" og finner skjæringspunktet mellom grafene til M og T, se punkt A. | |||
[[File: 2P_v20_1b.png]] | |||
Daglengden var lik i de to byene omtrent 79 døgn etter 31 desember, det vil si 20. mars 2019. | |||
Utregning av dato: 79-31-28=20. Dette som følge av at det er 31 dager i januar, og 28 dager i februar (2019 er ikke et skuddår). | |||
===c)=== | |||
Lager punktet $B=(0,M(0))$ for 31.desember, og punktet $C=(121,M(121))$ for 1.mai. | |||
For å finne x-verdien i punkt C beregner vi 31 dager i januar + 28 dager i februar + 31 dager i mars + 30 dager i april + 1 dag til 1. mai. Jeg velger her å ta med 1. mai, men det er mulig å la være. | |||
Lager linjen f mellom punkt B og C ved å bruke knappen "Linje". Finner stigningstallet a til linjen f ved knappen "Stigning". Man kan også se stigningstallet ut fra likningen til linjen f. Stigningstallet er omtrent 4,6 minutter per dag. | |||
[[File: 2P_v20_1c2.png]] | |||
Daglengden i Mandal økte i gjennomsnitt med 4,6 minutter per dag fra 31. desember til 1. mai. | |||
===d)=== | |||
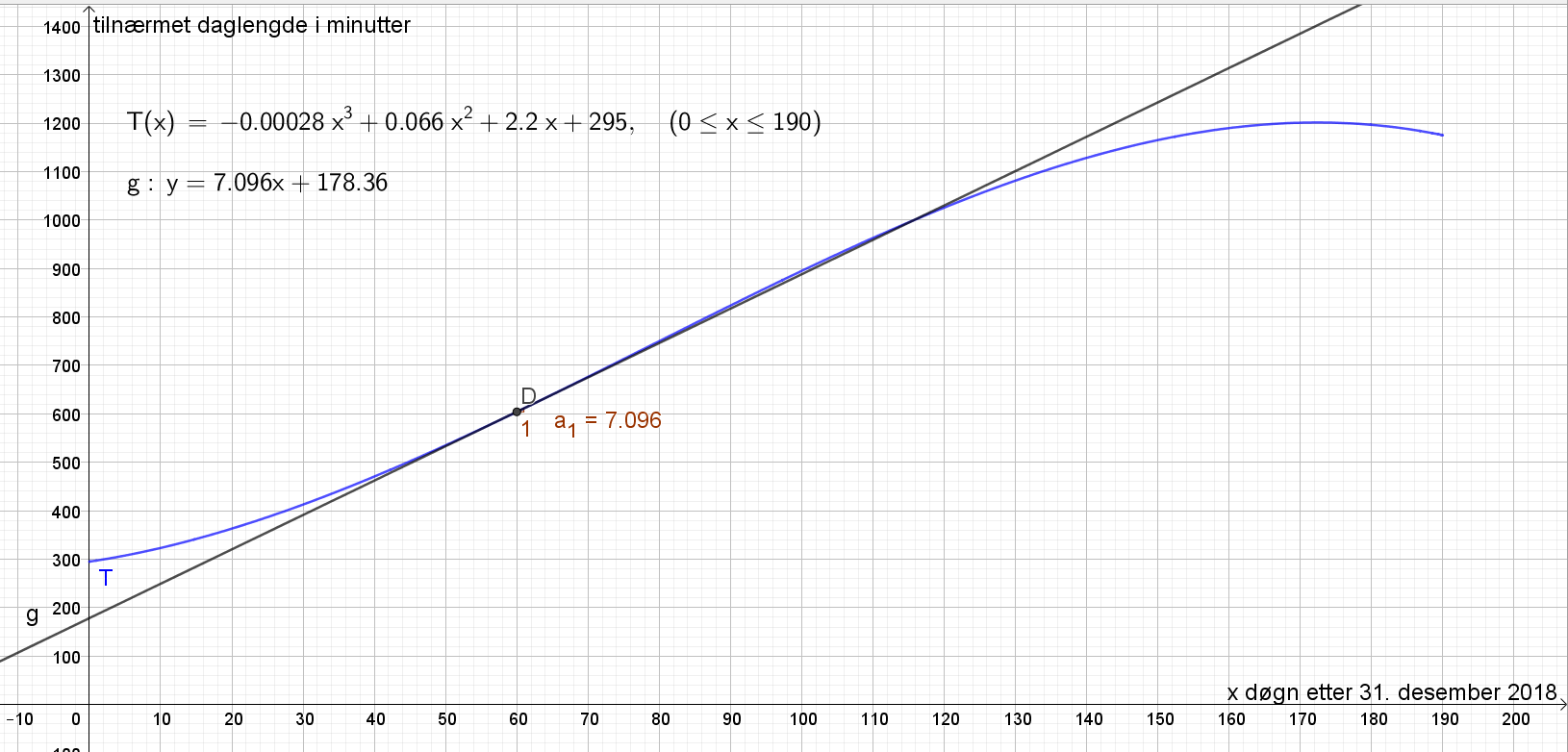
Lager punktet $D=(60,T(60))$ og lager tangenten g ved hjelp av knappen "Tangenter". Jeg finner stigningstallet a til tangenten ved å bruke knappen "Stigningstall". Jeg kan også se stigningstallet av funksjonsuttrykket for linjen g. Stigningstallet er omtrent 7,1 minutter per døgn. | |||
[[File: 2P_v20_1d.png]] | |||
Stigningstallet forteller oss at daglengden i Trondheim øker med 7,1 minutter per døgn den 1.mars. | |||
Utregning for å finne dato: 60-31-28 = 1. Dette som følge av at det er 31 dager i januar, og 28 dager i februar (2019 er ikke et skuddår). | |||
==Oppgave 2== | |||
<b>Diagram 1</b> | |||
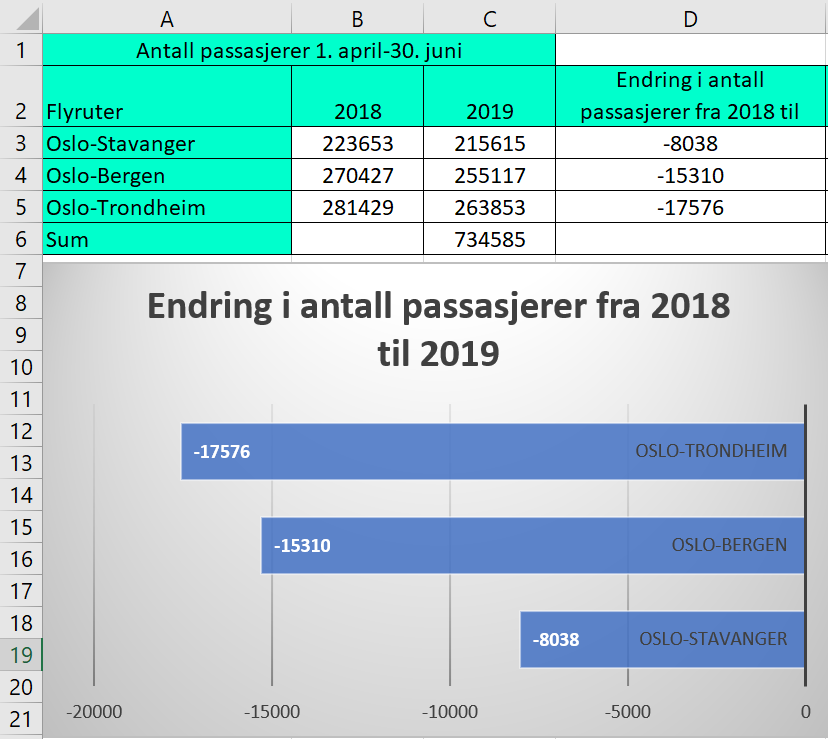
Bruker Excel for å beregne endring i antall passasjerer fra 2018 til 2019, og lage et passende diagram. | |||
[[File: 2P_v20_2-1.png]] | |||
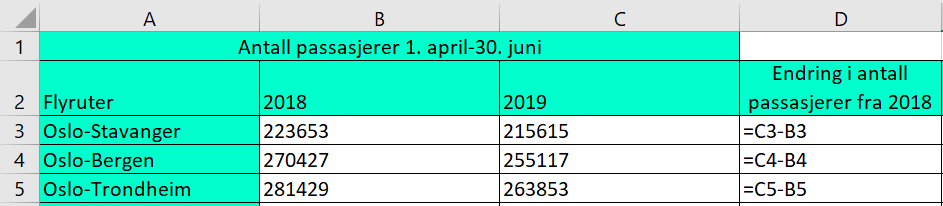
Med formler: | |||
[[File: 2P_v20_2-2.png]] | |||
<b>Diagram 2</b> | |||
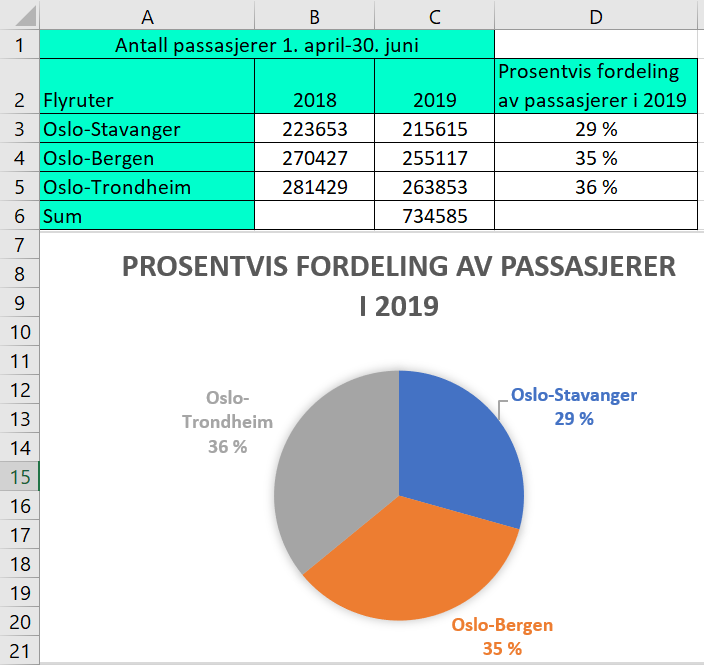
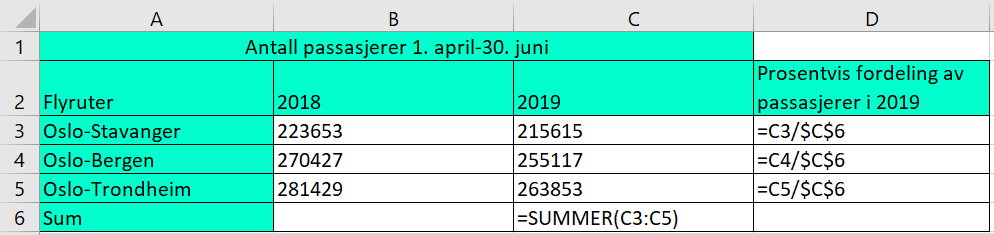
Bruker Excel for å beregne den prosentvise fordelingen av passasjerer mellom de tre flyrutene i 2019. | |||
[[File: 2P_v20_2-3.png]] | |||
Med formler: | |||
[[File: 2P_v20_2-4.png]] | |||
==Oppgave 3== | |||
$100000\cdot 1,0185^{-5}=91242$ | |||
Aina hadde 91242 kr på konto for 5 år siden. | |||
==Oppgave 4== | |||
===a)=== | |||
Lars sin modell skal øke med et fast antall hoppekreps hver dag, det vil si at han lager en lineær modell. | |||
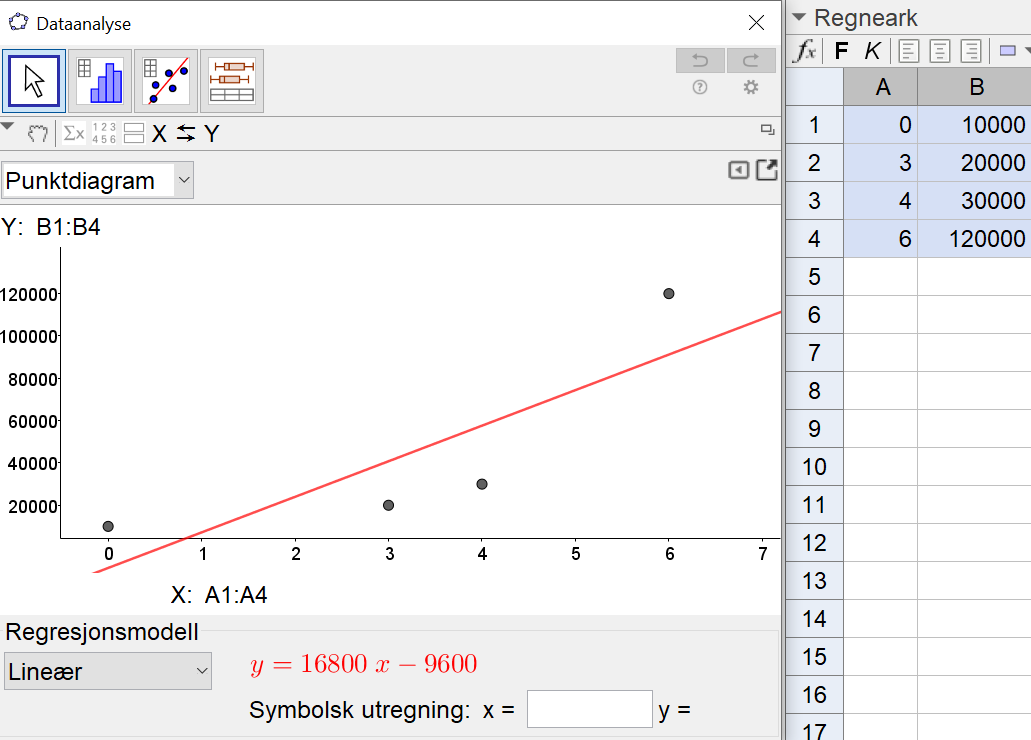
Jeg bruker regresjonsanalyse i Geogebra til å finne en lineær modellen ut fra datapunktene vi har. | |||
[[File: 2P_v20_4a.png]] | |||
Den lineære modellen er $y= 16800x-9600$ | |||
Stigningstallet betyr at antallet øker med 16800 hoppekreps per dag. | |||
Konstantleddet betyr at i x=0 (den 30. april) var antall hoppekreps -9600. Det stemmer ikke med observasjonen til Lars og Lene, og det er heller ikke mulig med et negativt antall hoppekreps. Modellen er ikke godt egnet til dette datasettet. | |||
===b)=== | |||
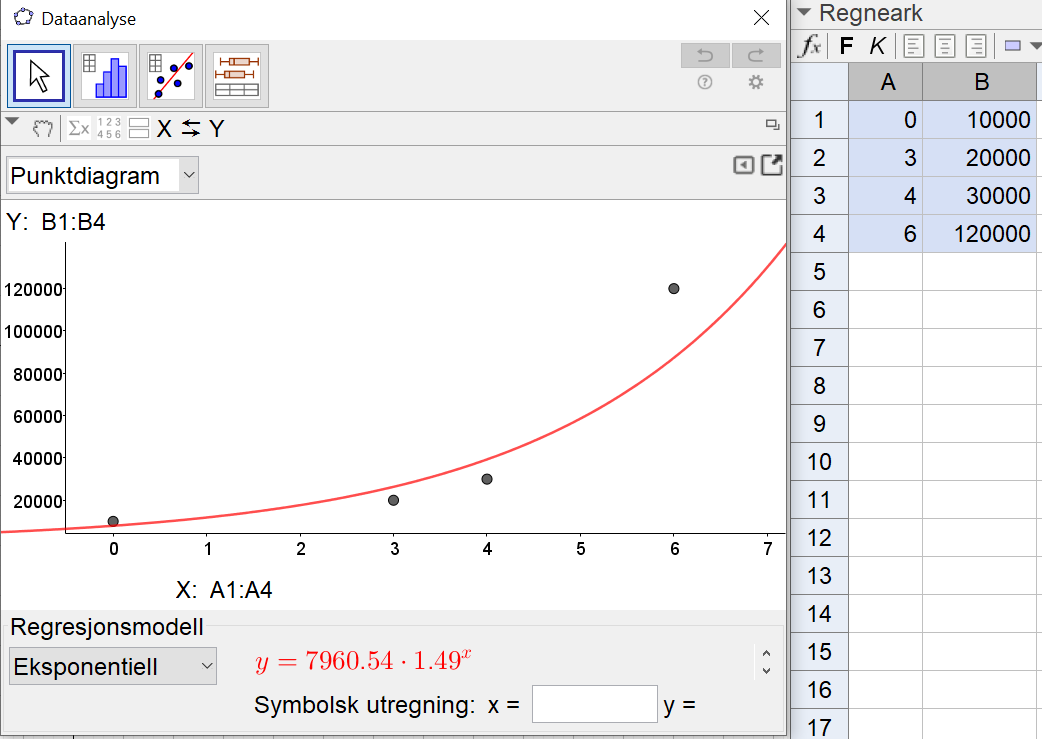
Lene sin modell skal øke med en fast prosent hver dag, det vil si at hun lager en eksponentiell modell. | |||
Jeg bruker regresjonsanalyse i Geogebra til å finne en eksponentiell modellen ut fra datapunktene vi har. | |||
[[File: 2P_v20_4b.png]] | |||
Den eksponentielle modellen er $f(x)=7961\cdot 1,49^x$ | |||
1,49 er vekstfaktoren, som vil si at antall hoppekreps øker med 49% per dag. | |||
7961 er antallet hoppekreps vi starter med i x=0 (den 30. april). Det stemmer ikke helt med observasjonen til Lars og Lene, men det er likevel en tilnærmet god nok modell til datasettet vi har. | |||
===c)=== | |||
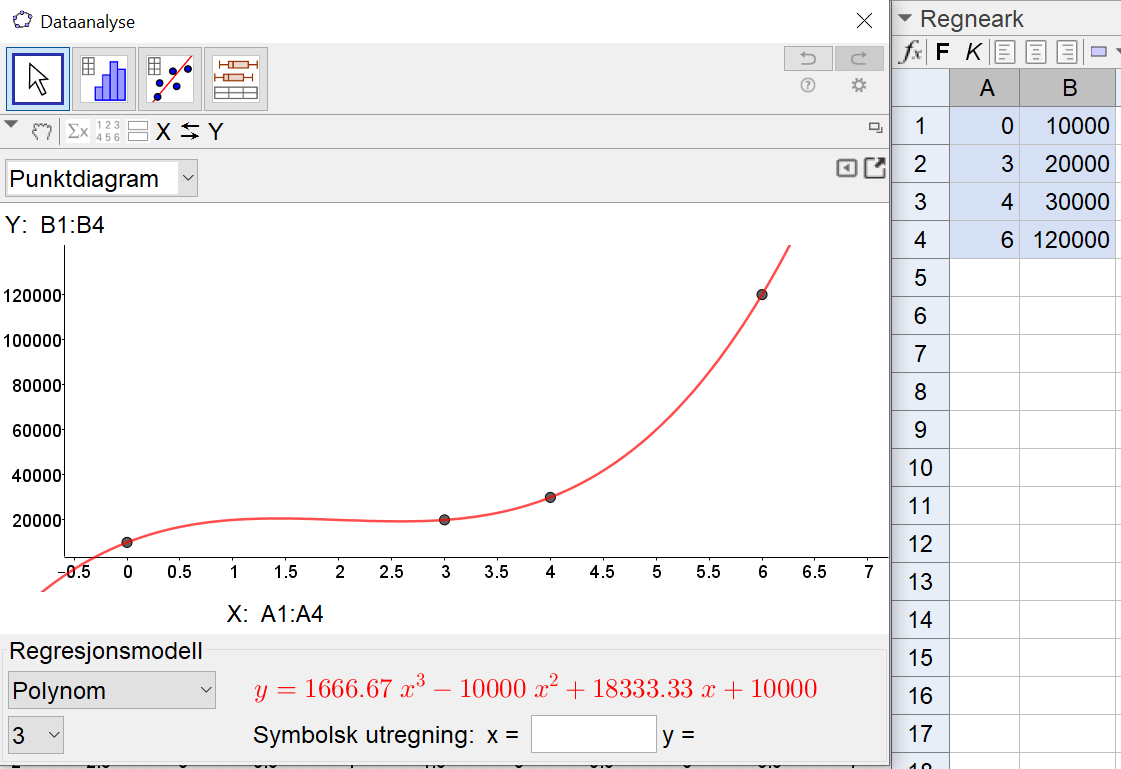
Jeg bruker regresjonsanalyse i Geogebra til å finne en polynomfunksjon av tredje grad som modell, ut fra datapunktene vi har. | |||
[[File: 2P_v20_5c.png]] | |||
===d)=== | |||
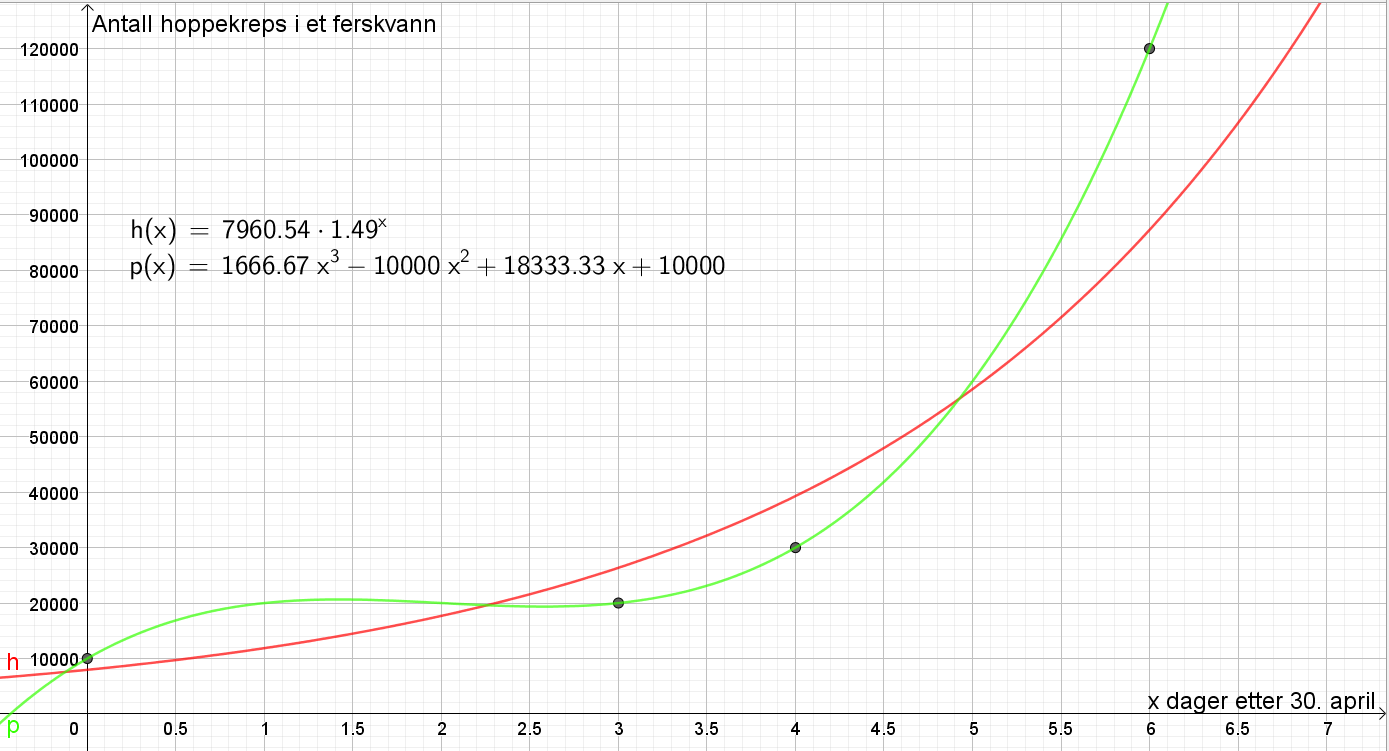
Bruker Geogebra til å tegne begge grafer. | |||
[[File: 2P_v20_4d2.png]] | |||
Grafen til <i>h</i> vokser i hele perioden og modellerer altså at antall hoppekreps stadig øker. | |||
Grafen til <i>p</i> har et lokalt toppunkt, og ifølge denne modellen synker faktisk antall hoppekreps i en kort periode, før antallet igjen vokser. | |||
Grafen til <i>p</i> passer godt til datapunktene vi har og grafen til <i>h</i> kan også modellere antall hoppekreps på en god måte. Begge modellene har omtrent riktig antall hoppekreps som startveri i x=0. | |||
Ingen av modellene er gyldige til evig tid, det er vanskelig å si hvordan hoppekrepspopulasjonen vil utvikle seg videre. Vi vet ikke om populasjonen stabiliserer seg på et visst antall individer, eller om antallet svinger opp og ned, eller til og med synker dramatisk. | |||
==Oppgave 5== | |||
===a)=== | |||
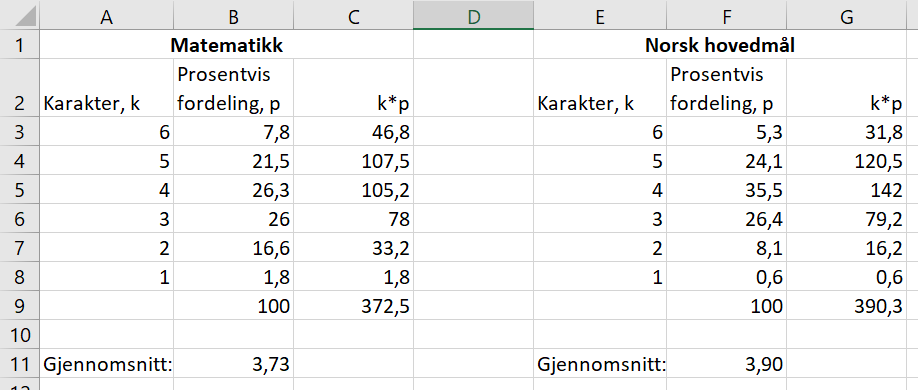
Bruker Excel til å regne ut gjennomsnittskarakterene. | |||
[[File: 2P_v20_5a.png]] | |||
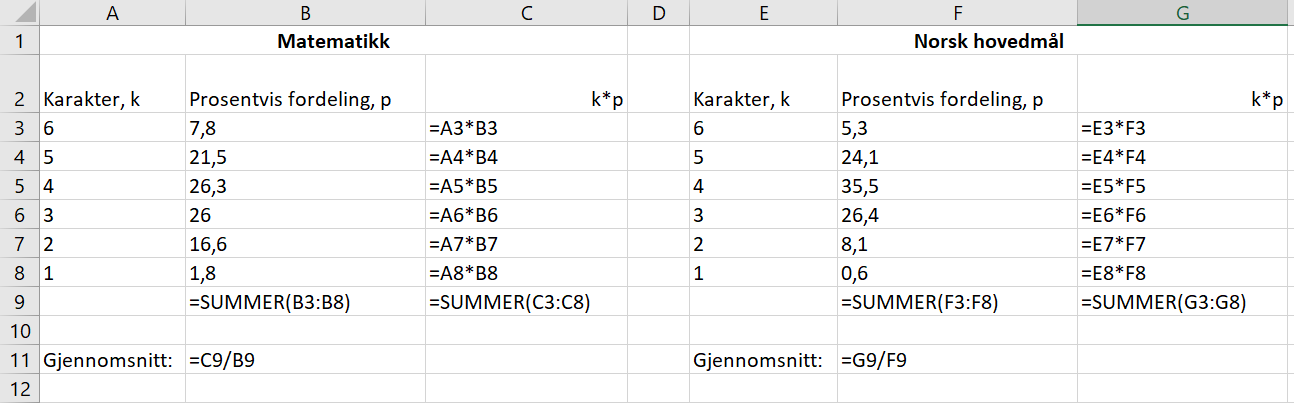
Med formler: | |||
[[File: 2P_v20_5a2.png]] | |||
Gjennomsnittskarakteren i matematikk er 3,73, og gjennomsnittskarakteren i norsk er 3,90. | |||
===b)=== | |||
Det er flere elever med karakter som avviker fra gjennomsnittet i matematikk enn i norsk, altså flere med karakter 1, 2 og 6. Derfor er standardavviket større i matematikk enn i norsk. Det er særlig mange flere med karakter 2, og færre med karakter 4 i matematikk enn i norsk. | |||
===c)=== | |||
Påstand 1) er feil. Størrelsen på gjennomsnittet påvirker ikke størrelsen på standardavviket. Det som påvirker størrelsen på standardavviket, er hvor mye verdiene avviker fra gjennomsnittet, og hvor mange verdier som avviker fra gjennomsnittet. | |||
Påstand 2) er riktig. Dersom ingen verdier avviker fra gjennomsnittet, er standardavviket lik null, og alle verdiene i datasettet er like. | |||
==Oppgave 6== | |||
===a)=== | |||
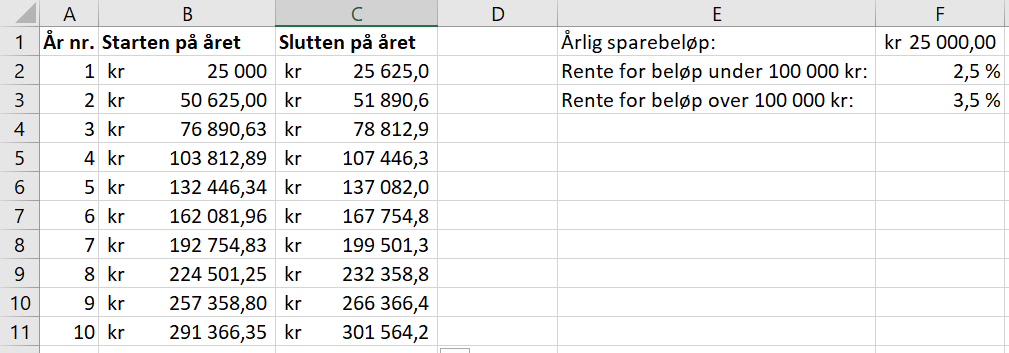
Bruker Excel for å løse oppgaven. | |||
[[File: 2P_v20_6.png]] | |||
Med formler: | |||
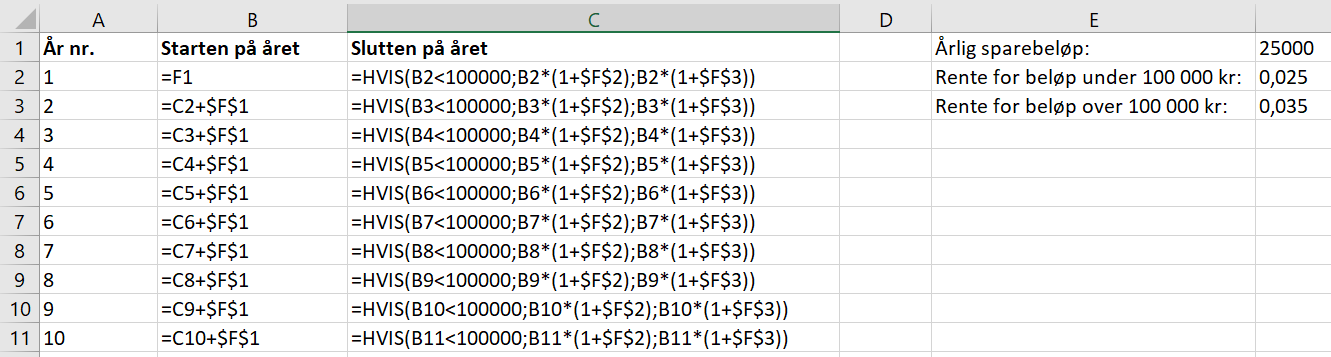
[[File: 2P_v20_6_2.png]] | |||
===b)=== | |||
$301564,2-(10\cdot 25000)=51564,2$ | |||
Linn har fått til sammen 51 564,2 kr i rente i løpet av disse 10 årene. | |||
==Oppgave 7== | |||
I graf A synker funksjonsverdien sakte til å begynne med, og raskere etter hvert. Det passer ikke med en eksponentiell funksjon. | |||
I graf B synker funksjonsverdien med en konstant størrelse for hver enhet langs x-aksen. Det passer ikke med en eksponentiell funksjon. | |||
Grafen C illustrerer en størrelse som avtar eksponentielt. For en størrelse som avtar eksponentielt, synker funksjonsverdien med en fast prosent av funksjonsverdien for hver enhet langs x-aksen. I starten synker funksjonsverdien derfor ganske raskt, og saktere avtar etter hvert. | |||
==Oppgave 8== | |||
Total vekstfaktor for Svein: $1,04\cdot 1,06=1,1024$. Det tilsvarer 10,24% lønnsøkning. | |||
Total vekstfaktor for Tore: $1,08\cdot 1,02=1,1016$. Det tilsvarer 10,16% lønnsøkning. | |||
Svein hadde <i>litt</i> høyere lønn enn Tore i 2019. | |||
Siste sideversjon per 13. mai 2021 kl. 07:46
Diskusjon av oppgaven på matteprat
Løsning del 1 laget av Kristian Saug
Løsning del 2 laget av Kristian Saug
Videoløsning del 1 av Lektor Lainz
Videoløsning del 2 av Lektor Lainz
DEL 1
Oppgave 1
a)
Skriver tallene i stigende rekkefølge:
$0\quad 0\quad 5\quad 5\quad 7\quad 7\quad 7\quad 7\quad 7\quad 7\quad 8\quad 8\quad 8\quad 8\quad 10\quad 10\quad 10\quad 10\quad 14\quad 14$
Medianen er gjennomsnittet av de to midterste tallene (siden det er et partall antall tall): $\frac{7+8}{2}=7,5$
Gjennomsnitt: $\frac{0\cdot 2 + 5\cdot 2+7\cdot 6+8\cdot 4 + 10\cdot 4 + 14\cdot 2}{20} =\frac{0+10+42+32+40+28}{20} =\frac{152}{20} = \frac{76}{10}=7,6$
Typetallet er det tallet som forekommer flest ganger: $7$
Variasjonsbredden = største verdi - minste verdi = $14 - 0 = 14$
b)
| Antall ganger en elev hjelper
til med husarbeid hjemme |
Frekvens | Kumulativ frekvens | Relativ Frekvens | Relativ kumulativ frekvens |
| 0 | 2 | 2 | 0,1 | 0,1 |
| 5 | 2 | 4 | 0,1 | 0,2 |
| 7 | 6 | 10 | 0,3 | 0,5 |
| 8 | 4 | 14 | 0,2 | 0,7 |
| 10 | 4 | 18 | 0,2 | 0,9 |
| 14 | 2 | 20 | 0,1 | 1 |
Tallene i nest siste rad:
Frekvens på 4 betyr at 4 elever i klassen svarte at de hjalp til 10 ganger med husarbeid i løpet av en uke.
Kumulativ frekvens på 18 betyr at 18 elever i klassen hjalp til opptil 10 ganger (mellom 0 og 10 ganger).
Relativ frekvens på 0,2 betyr at 20% av elevene hjalp til 10 ganger.
Relativ kumulativ frekvens på 0,9 betyr at 90% av elevene hjalp til opptil 10 ganger (mellom 0 og 10 ganger).
Oppgave 2
a)
Det er en prisforskjell på 60 kr mellom flybussen og bybanen, og flybussen koster 100 kr.
$\frac{60}{100}=60$%
Bybanen er 60% billigere sammenlignet med flybussen.
b)
Det er en prisforskjell på 60 kr mellom flybussen og bybanen, og bybanen koster 40 kr.
$\frac{60}{40}=\frac{3}{2}=1,5 = 150$%
Flybussen er 150% dyrere sammenlignet med bybanen.
Oppgave 3
Lineær vekst vil si at vi har en fast startverdi (konstantledd), og deretter en konstant vekst per enhet (et konstant stigningstall). Et eksempel er en drosjetur der hvor startprisen er 60 kr, og prisen per km er 16 kr. Vi kan da uttrykket prisen for turen, y, etter x km kjørt, ved $y=16x+60$
Eksponentiell vekst vil si at vi har en fast startverdi, og deretter en prosentvis økning per enhet. Et eksempel er en leilighet som koster 3.000.000 kr, og hvor prisen går opp med 1,5% per år. Vi kan da uttrykke prisen på leiligheten, f(x), etter x år ved $f(x)=3000000\cdot 1,015^x$
Oppgave 4
Gjør om tonn til gram: $45$ tonn $= 45 000 000$ g
Regner ut antall hengelåser: $\frac{45 000 000}{50}=900 000 = 9\cdot 10^5$
Det var omtrent $ 9\cdot 10^5$ hengelåser på rekkverket.
Oppgave 5
a)
| Poeng | Klassemidtpunkt, m | Antall elever, a | $m\cdot a$ |
| $[ \, 0,10 \rangle$ | 5 | 4 | 20 |
| $[ \, 10,20 \rangle$ | 15 | 12 | 180 |
| $[ \, 20,30 \rangle$ | 25 | 34 | 850 |
| $[ \, 30,40 \rangle$ | 35 | 30 | 1050 |
| $[ \, 40,60 \rangle$ | 50 | 20 | 1000 |
| Sum | 100 | 3100 |
Gjennomsnitt: $\frac{3100}{100}=31$
Gjennomsnittlig antall poeng på kartleggingsprøven var 31.
b)
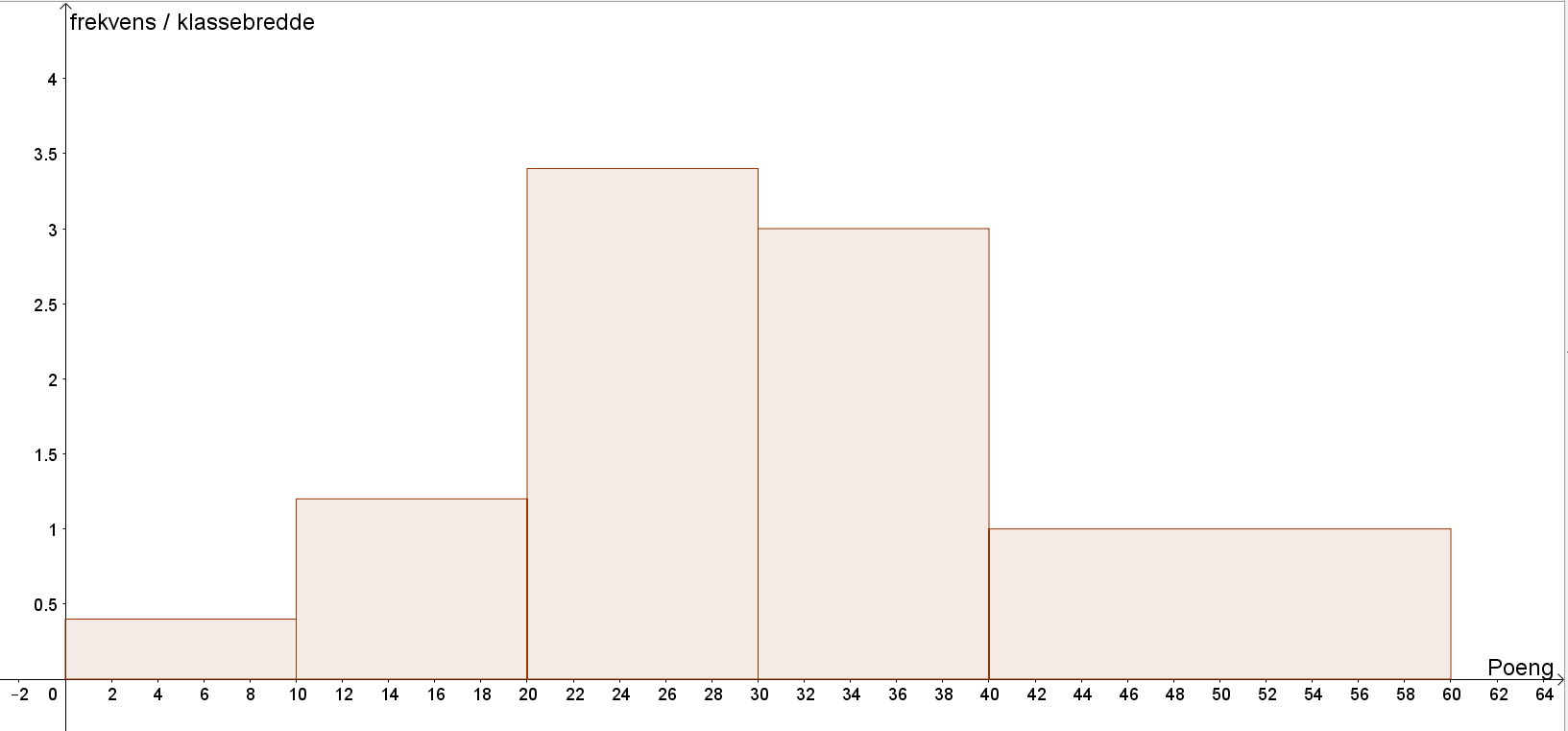
Beregninger for å lage histogram:
| Poeng | Klassebredde | Antall elever (frekvens) | Frekvens / klassebredde |
| $[ \, 0,10 \rangle$ | 10 | 4 | 0,4 |
| $[ \, 10,20 \rangle$ | 10 | 12 | 1,2 |
| $[ \, 20,30 \rangle$ | 10 | 34 | 3,4 |
| $[ \, 30,40 \rangle$ | 10 | 30 | 3 |
| $[ \, 40,60 \rangle$ | 20 | 20 | 1 |
Histogram (som du må tegne for hånd):
Oppgave 6
a)
$f(x)=200000\cdot 0,95^{10}$
b)
Dersom båtens verdi sank med 10 000 kr per år i 10 år, ville den hatt et totalt verditap på 100 000 kr, og være verdt 100 000 kr om 10 år. Men dette er ikke tilfellet, båtens verdi synker prosentvis hvert år, og båtens verditap blir derfor lavere og lavere for hvert år.
Nærmere forklart: det første året minker verdien av båten med 5% av 200 000 kr, altså 10000 kr. Det andre året er verdien av båten 190 000 kr, og verdien av båten synker fremdeler med 5% hvert år. 5% av 190 000 kr er 9500 kr, det vil si at båtens verdi synker med mindre enn 10 000 kr det andre året. Båtens verdi blir lavere og lavere for hvert år, og 5% av verdien blir et lavere og lavere verditap for hvert år. Båtens verdi synker altså ikke med 10 000 kr hvert år, og det totale verditapet etter 10 år blir lavere enn 100 000 kr. Båten er verdt mer enn 100 000 kr etter 10 år.
Oppgave 7
a)
Jeg bruker tabell for å få en oversikt både til oppgave a) og b).
| Figur 1 | Figur 2 | Figur 3 | Figur 10 | Figur n | |
| Antall grønne kvadrater | $2\cdot 4=8$ | $3\cdot 4=12$ | $4\cdot 4=16$ | $11\cdot 4=44$ | $(n+1)\cdot 4$ |
| Antall hvite kvadrater | $1^2=1$ | $2^2=4$ | $3^3=9$ | $10^2=100$ | $n^2$ |
Det er 44 grønne kvadrater i figur 10, se utregning i tabellen.
b)
Et uttrykk for antall grønne kvadrater når antall små hvite kvadrater er $n^2$:
$(n+1)\cdot 4 \\= 4n+4$
Se tabellen i a) for tankegangen bak.
DEL 2
Oppgave 1
a)
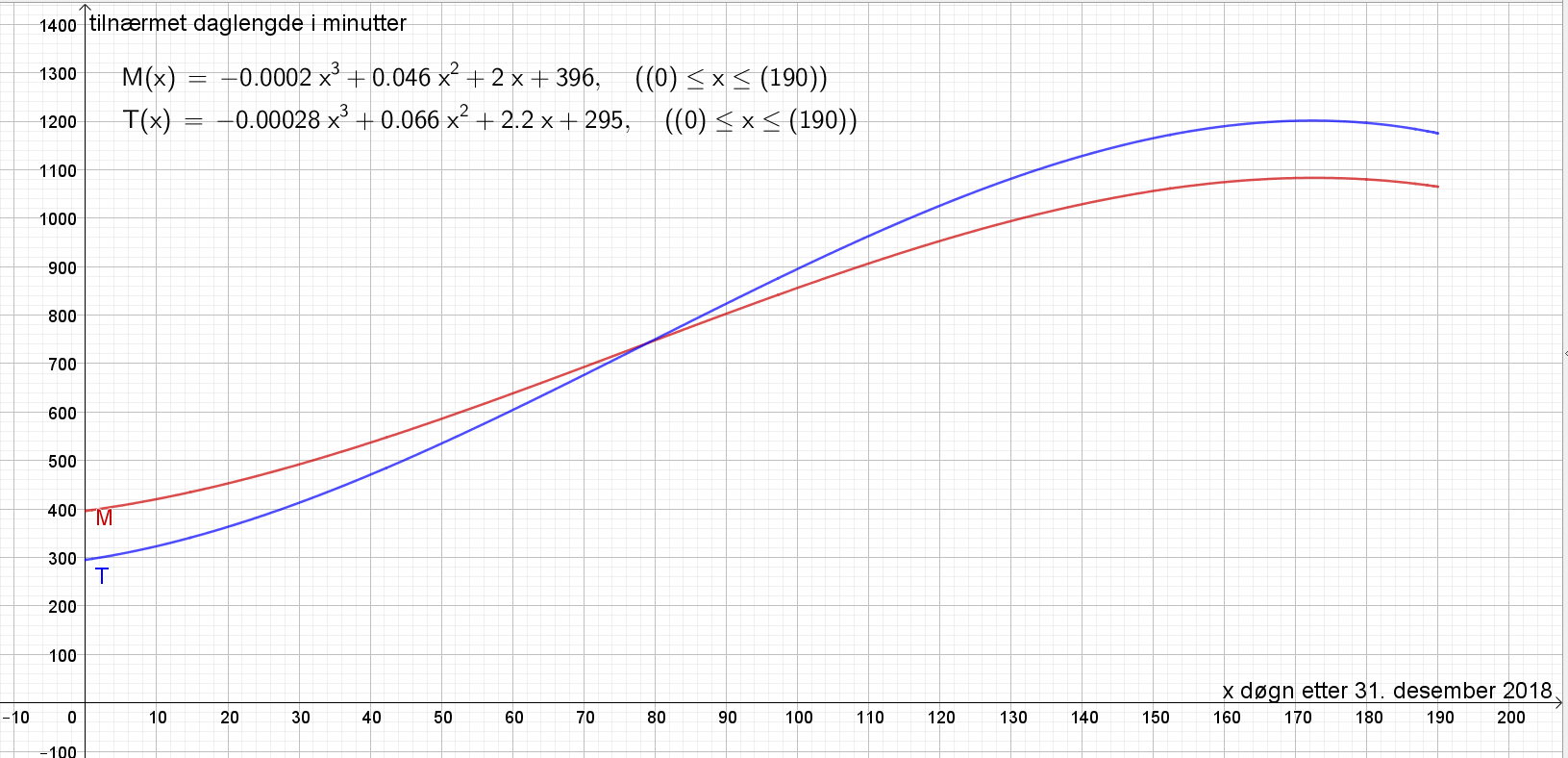
Bruker Geogebra for å tegne grafene til M og T.
b)
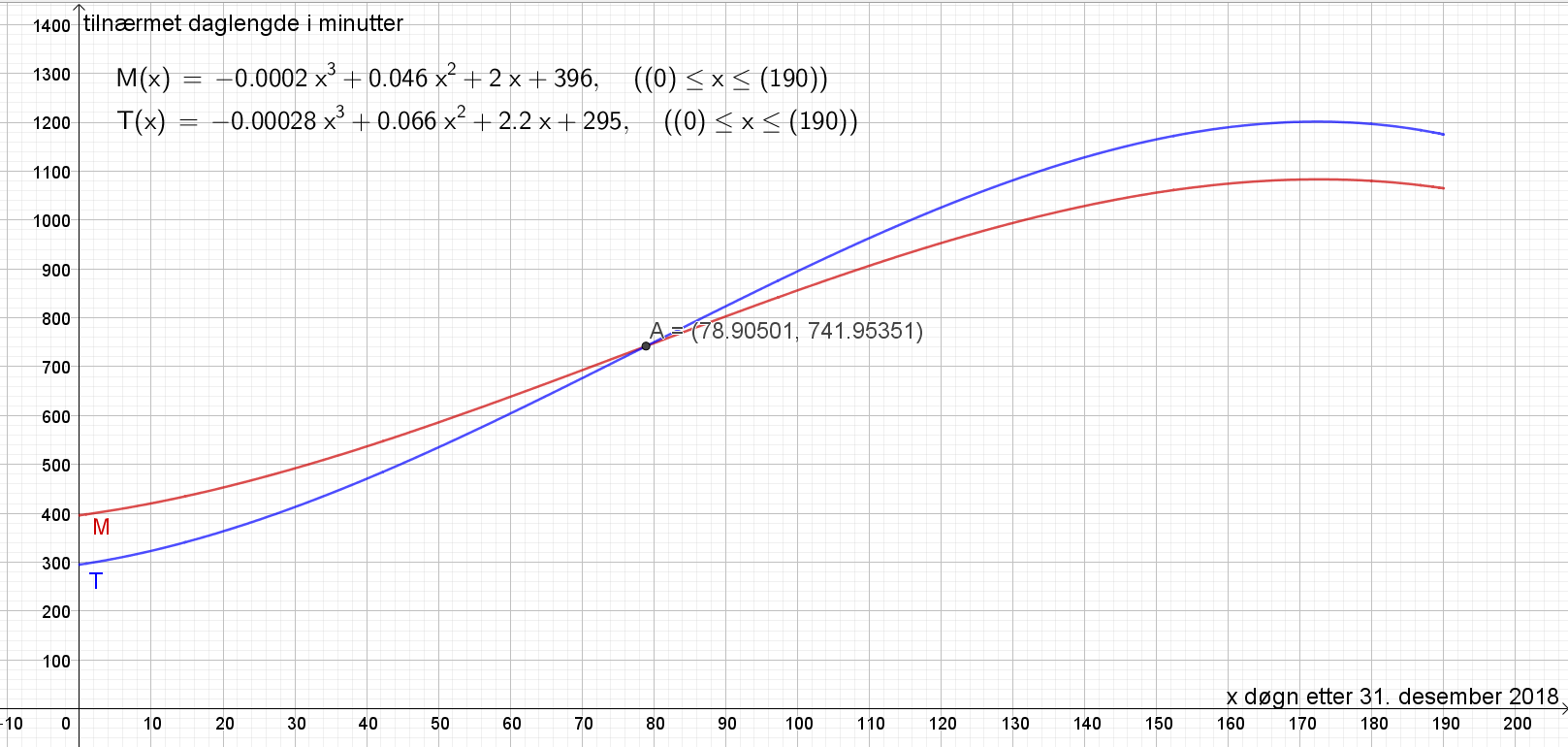
Bruker "skjæringspunkt mellom to objekt" og finner skjæringspunktet mellom grafene til M og T, se punkt A.
Daglengden var lik i de to byene omtrent 79 døgn etter 31 desember, det vil si 20. mars 2019.
Utregning av dato: 79-31-28=20. Dette som følge av at det er 31 dager i januar, og 28 dager i februar (2019 er ikke et skuddår).
c)
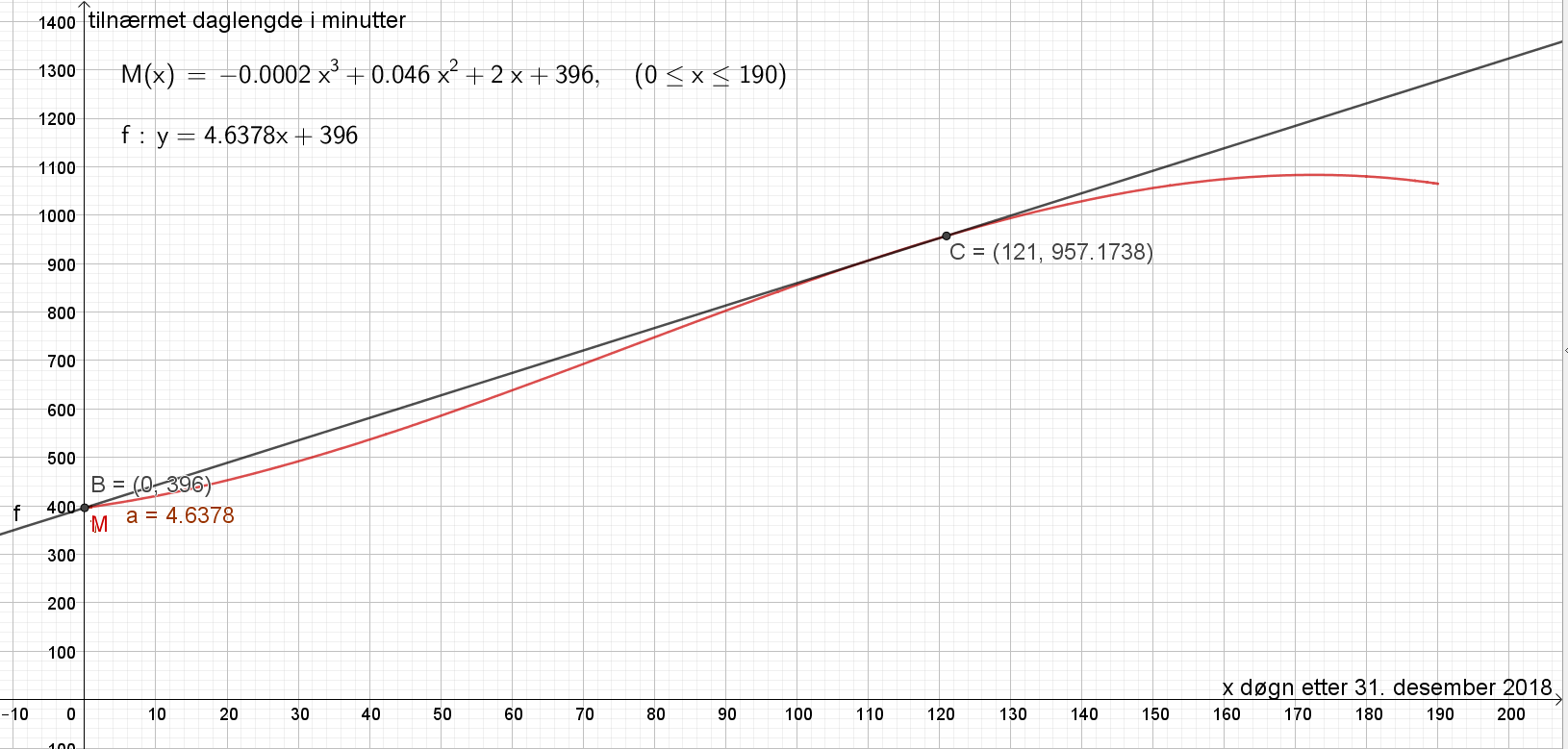
Lager punktet $B=(0,M(0))$ for 31.desember, og punktet $C=(121,M(121))$ for 1.mai.
For å finne x-verdien i punkt C beregner vi 31 dager i januar + 28 dager i februar + 31 dager i mars + 30 dager i april + 1 dag til 1. mai. Jeg velger her å ta med 1. mai, men det er mulig å la være.
Lager linjen f mellom punkt B og C ved å bruke knappen "Linje". Finner stigningstallet a til linjen f ved knappen "Stigning". Man kan også se stigningstallet ut fra likningen til linjen f. Stigningstallet er omtrent 4,6 minutter per dag.
Daglengden i Mandal økte i gjennomsnitt med 4,6 minutter per dag fra 31. desember til 1. mai.
d)
Lager punktet $D=(60,T(60))$ og lager tangenten g ved hjelp av knappen "Tangenter". Jeg finner stigningstallet a til tangenten ved å bruke knappen "Stigningstall". Jeg kan også se stigningstallet av funksjonsuttrykket for linjen g. Stigningstallet er omtrent 7,1 minutter per døgn.
Stigningstallet forteller oss at daglengden i Trondheim øker med 7,1 minutter per døgn den 1.mars.
Utregning for å finne dato: 60-31-28 = 1. Dette som følge av at det er 31 dager i januar, og 28 dager i februar (2019 er ikke et skuddår).
Oppgave 2
Diagram 1
Bruker Excel for å beregne endring i antall passasjerer fra 2018 til 2019, og lage et passende diagram.
Med formler:
Diagram 2
Bruker Excel for å beregne den prosentvise fordelingen av passasjerer mellom de tre flyrutene i 2019.
Med formler:
Oppgave 3
$100000\cdot 1,0185^{-5}=91242$
Aina hadde 91242 kr på konto for 5 år siden.
Oppgave 4
a)
Lars sin modell skal øke med et fast antall hoppekreps hver dag, det vil si at han lager en lineær modell.
Jeg bruker regresjonsanalyse i Geogebra til å finne en lineær modellen ut fra datapunktene vi har.
Den lineære modellen er $y= 16800x-9600$
Stigningstallet betyr at antallet øker med 16800 hoppekreps per dag.
Konstantleddet betyr at i x=0 (den 30. april) var antall hoppekreps -9600. Det stemmer ikke med observasjonen til Lars og Lene, og det er heller ikke mulig med et negativt antall hoppekreps. Modellen er ikke godt egnet til dette datasettet.
b)
Lene sin modell skal øke med en fast prosent hver dag, det vil si at hun lager en eksponentiell modell.
Jeg bruker regresjonsanalyse i Geogebra til å finne en eksponentiell modellen ut fra datapunktene vi har.
Den eksponentielle modellen er $f(x)=7961\cdot 1,49^x$
1,49 er vekstfaktoren, som vil si at antall hoppekreps øker med 49% per dag.
7961 er antallet hoppekreps vi starter med i x=0 (den 30. april). Det stemmer ikke helt med observasjonen til Lars og Lene, men det er likevel en tilnærmet god nok modell til datasettet vi har.
c)
Jeg bruker regresjonsanalyse i Geogebra til å finne en polynomfunksjon av tredje grad som modell, ut fra datapunktene vi har.
d)
Bruker Geogebra til å tegne begge grafer.
Grafen til h vokser i hele perioden og modellerer altså at antall hoppekreps stadig øker. Grafen til p har et lokalt toppunkt, og ifølge denne modellen synker faktisk antall hoppekreps i en kort periode, før antallet igjen vokser.
Grafen til p passer godt til datapunktene vi har og grafen til h kan også modellere antall hoppekreps på en god måte. Begge modellene har omtrent riktig antall hoppekreps som startveri i x=0.
Ingen av modellene er gyldige til evig tid, det er vanskelig å si hvordan hoppekrepspopulasjonen vil utvikle seg videre. Vi vet ikke om populasjonen stabiliserer seg på et visst antall individer, eller om antallet svinger opp og ned, eller til og med synker dramatisk.
Oppgave 5
a)
Bruker Excel til å regne ut gjennomsnittskarakterene.
Med formler:
Gjennomsnittskarakteren i matematikk er 3,73, og gjennomsnittskarakteren i norsk er 3,90.
b)
Det er flere elever med karakter som avviker fra gjennomsnittet i matematikk enn i norsk, altså flere med karakter 1, 2 og 6. Derfor er standardavviket større i matematikk enn i norsk. Det er særlig mange flere med karakter 2, og færre med karakter 4 i matematikk enn i norsk.
c)
Påstand 1) er feil. Størrelsen på gjennomsnittet påvirker ikke størrelsen på standardavviket. Det som påvirker størrelsen på standardavviket, er hvor mye verdiene avviker fra gjennomsnittet, og hvor mange verdier som avviker fra gjennomsnittet.
Påstand 2) er riktig. Dersom ingen verdier avviker fra gjennomsnittet, er standardavviket lik null, og alle verdiene i datasettet er like.
Oppgave 6
a)
Bruker Excel for å løse oppgaven.
Med formler:
b)
$301564,2-(10\cdot 25000)=51564,2$
Linn har fått til sammen 51 564,2 kr i rente i løpet av disse 10 årene.
Oppgave 7
I graf A synker funksjonsverdien sakte til å begynne med, og raskere etter hvert. Det passer ikke med en eksponentiell funksjon.
I graf B synker funksjonsverdien med en konstant størrelse for hver enhet langs x-aksen. Det passer ikke med en eksponentiell funksjon.
Grafen C illustrerer en størrelse som avtar eksponentielt. For en størrelse som avtar eksponentielt, synker funksjonsverdien med en fast prosent av funksjonsverdien for hver enhet langs x-aksen. I starten synker funksjonsverdien derfor ganske raskt, og saktere avtar etter hvert.
Oppgave 8
Total vekstfaktor for Svein: $1,04\cdot 1,06=1,1024$. Det tilsvarer 10,24% lønnsøkning.
Total vekstfaktor for Tore: $1,08\cdot 1,02=1,1016$. Det tilsvarer 10,16% lønnsøkning.
Svein hadde litt høyere lønn enn Tore i 2019.