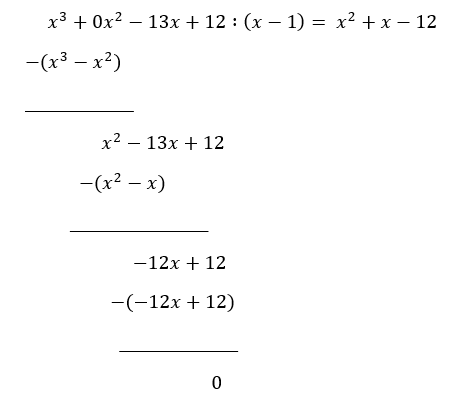R1 2018 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| (37 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 8: | Linje 8: | ||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHVZoWZ3vh89Jil5_D73IyaZ Løsning som video av Lektor Håkon Raustøl] | [https://www.youtube.com/playlist?list=PLplkS_rtcCHVZoWZ3vh89Jil5_D73IyaZ Løsning som video av Lektor Håkon Raustøl] | ||
[https://youtu.be/v20rWpDv7y8 Løsning del 1 som video av Lainz] | |||
[https://youtu.be/N77a8V57QIA Løsning del 2 som video av Lainz] | |||
=DEL 1= | |||
==Oppgave 1== | |||
===a)=== | |||
$f(x)=x^4-x+2$ | |||
$f'(x)=4x^3-1$ | |||
===b)=== | |||
$g(x)=x^3\cdot ln(x)$ | |||
$g'(x)=3x^2\cdot ln(x) + x^3 \cdot \frac{1}{x} = 3x^2ln(x)+x^2$ | |||
===c)=== | |||
$h(x)=e^{2x^2+x}$ | |||
$h'(x)=(4x+1)e^{2x^2+x}$ | |||
==Oppgave 2== | |||
===a)=== | |||
$\frac{1}{2x-2}+\frac{2}{x-3}-\frac{x-2}{x^2-4x+3} \\ = \frac{1\cdot \color{blue}{(x-3)}}{2(x-1)\color{blue}{(x-3)}}+\frac{2\cdot \color{red}{2(x-1)}}{\color{red}{2(x-1)}(x-3)}-\frac{\color{orange}{2}(x-2)}{\color{orange}{2}(x-1)(x-3)} \\ =\frac{ (x-3) + (4x-4) - (2x-4)}{2(x-1)(x-3)} \\ = \frac{x+4x-2x -3-4+4}{2(x-1)(x-3)} \\ = \frac{3x-3}{2(x-1)(x-3)} \\ = \frac{3(x-1)}{2(x-1)(x-3)} \\ = \frac{3}{2(x-3)} \\ = \frac{3}{2x-6}$ | |||
===b)=== | |||
$2ln(x\cdot y^3)-\frac{1}{2}ln(\frac{x^4}{y^2}) \\ = 2(ln(x)+ln(y^3))-\frac{1}{2}(ln(x^4)-ln(y^2)) \\= 2(ln(x)+3ln(y))-\frac{1}{2}(4ln(x)-2ln(y)) \\= 2ln(x)+6ln(y)-2ln(x)+ln(y) \\= 7ln(y)$ | |||
==Oppgave 3== | |||
Vi har punktene <i> A(-2,-1), B(-1, -3), C(3, -1) og D(t,t^2+2) </i> der $t\in R$. | |||
===a)=== | |||
$\vec{AB} = [-1-(-2), -3-(-1)] = [1, -2]$ | |||
$\vec{BC} = [3-(-1), -1-(-3)] = [4, 2]$ | |||
===b)=== | |||
$[1,-2]\cdot[4,2] = 1\cdot 4 + (-2)\cdot 2 = 4-4 = 0$ | |||
Skalarproduktet av $\vec{AB}$ og $\vec{BC}$ er 0, og vi har derfor $\vec{AB}\perp\vec{BC}$ | |||
===c)=== | |||
$\vec{CD}=[t-3, t^2+2-(-1)] = [t-3, t^2+3]$ | |||
Dersom $\vec{CD}\| \vec{AB}$, så er $\vec{CD} = k\cdot\vec{AB}$ | |||
$[t-3,t^2+3]=k\cdot[1,-2]$ | |||
Vi får likningssettet: | |||
$I \quad t-3 = k$ | |||
$II \quad t^2+3=-2k$ | |||
$II \quad t^2+3 = -2 (t-3) \\ \quad t^2 + 3 = -2t+6 \\ \quad t^2 + 2t -3 = 0 \\ \quad (t+3)(t-1) = 0 \\ \quad t = -3 \vee t = 1$ | |||
$\vec{CD}\| \vec{AB}$ når $ t = -3 \vee t = 1$. | |||
==Oppgave 4== | |||
Vi har $f(x)=x^3+k\cdot x + 12$ | |||
===a)=== | |||
Dersom $f(x):(x-1)$ skal gå opp, er x=1 et nullpunkt. | |||
$f(1)=0 \\ 1^3+k\cdot 1 + 12 = 0 \\ k+13 = 0 \\ k=-13$ | |||
===b)=== | |||
Vi har nå $f(x)=x^3-13x+12$ | |||
Utfører polynomdivisjonen: | |||
[[File: R1_V18_del1_4b.png]] | |||
$f(x)=(x^2+x-12)(x-1) = (x-3)(x-1)(x+4)$ | |||
===c)=== | |||
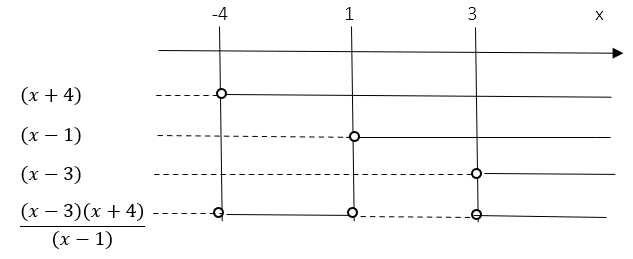
$\frac{x^2+x-12}{x-1} \geq 0 \\ \frac{(x-3)(x+4)}{x-1} \geq 0$ | |||
[[File: R1_V18_del1_4c.png]] | |||
$\frac{x^2+x-12}{x-1} \geq 0$ nå $x\in [-4,1]\cup [3,\rightarrow \rangle$ | |||
==Oppgave 5== | |||
D = defekt | |||
===a)=== | |||
$P(A \cap D) = 0,40 \cdot 0,03 = 0,012 = 1,2 \%$ | |||
Sannsynligheten for at laderen kommer fra leverandør A og er defekt, er 1,2%. | |||
===b)=== | |||
$P(D)=P(D|A)\cdot P(A) + P(D|B)\cdot P(B) \\= 0,03\cdot 0,40 + 0,02 \cdot 0,60 = 0,012 + 0,012 = 0,024$ | |||
$P(A | D) = \frac{P(A) \cdot P(D|A)}{P(D)} = \frac{0,40 \cdot 0,03}{0,024} = \frac{0,012}{0,024} = 0,5 = 50\%$ | |||
Sannsynligheten for at en lader som er defekt, kommer fra leverandør A, er 50%. | |||
==Oppgave 6== | |||
Vi har $f(x)=e^{2x}-4e^x+3$ | |||
===a)=== | |||
$f(x)=0 \\ e^{2x}-4e^x+3 = 0 \\ \text{Setter} \,u = e^x \\ u^2 - 4u + 3 = 0 \\ (u-1)(u-3)=0 \\ u= 1 \vee u = 3 \\ e^x = 1 \vee e^x = 3 \\ x = ln 1 \vee x = ln 3 \\ x = 0 \vee x \approx 1,10 $ | |||
Nullpunktene til <i>f</i> er (0,0) og (1.10, 0). | |||
===b)=== | |||
$f'(x)= 2e^{2x}-4e^x$ | |||
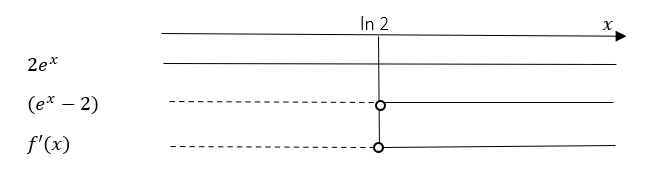
$f'(x)=0 \\ 2e^{2x}-4e^x = 0 \\ 2e^x(e^x-2)\\ 2e^x = 0 \vee e^x = 2 \\ \xcancel{x = ln 0} \vee x = ln 2 \\ x = ln 2 \approx 0,69$ | |||
Forkaster $x = ln 0$ da $ln 0 $ ikke er definert. | |||
[[File: R1_V18_del1_6b.png ]] | |||
Finner funksjonsverdien i x = ln 2. | |||
$f(ln 2) = e^{2(ln2)}-4e^{ln2} + 3 = e^{ln2^2}-4\cdot 2 + 3 = 4-8+3 = -1$ | |||
Grafen til <i>f</i> har et bunnpunkt i (0.69, -1). | |||
===c)=== | |||
$f' '(x)=4e^{2x}-4e^x = 4e^x(e^x-1)$ | |||
$f' '(x)=0 \\ 4e^x(e^x-1) = 0 \\ 4e^x = 0 \vee e^x = 1 \\ \xcancel{x = ln0} \vee x=ln1 \\ x=0$ | |||
Finner funksjonsverdien i x = 0. | |||
$f(0)=e^{2\cdot 0}-4e^0+3 = 1-4+3 = 0$ | |||
Grafen til <i>f</i> har et vendepunkt i (0,0). | |||
===d)=== | |||
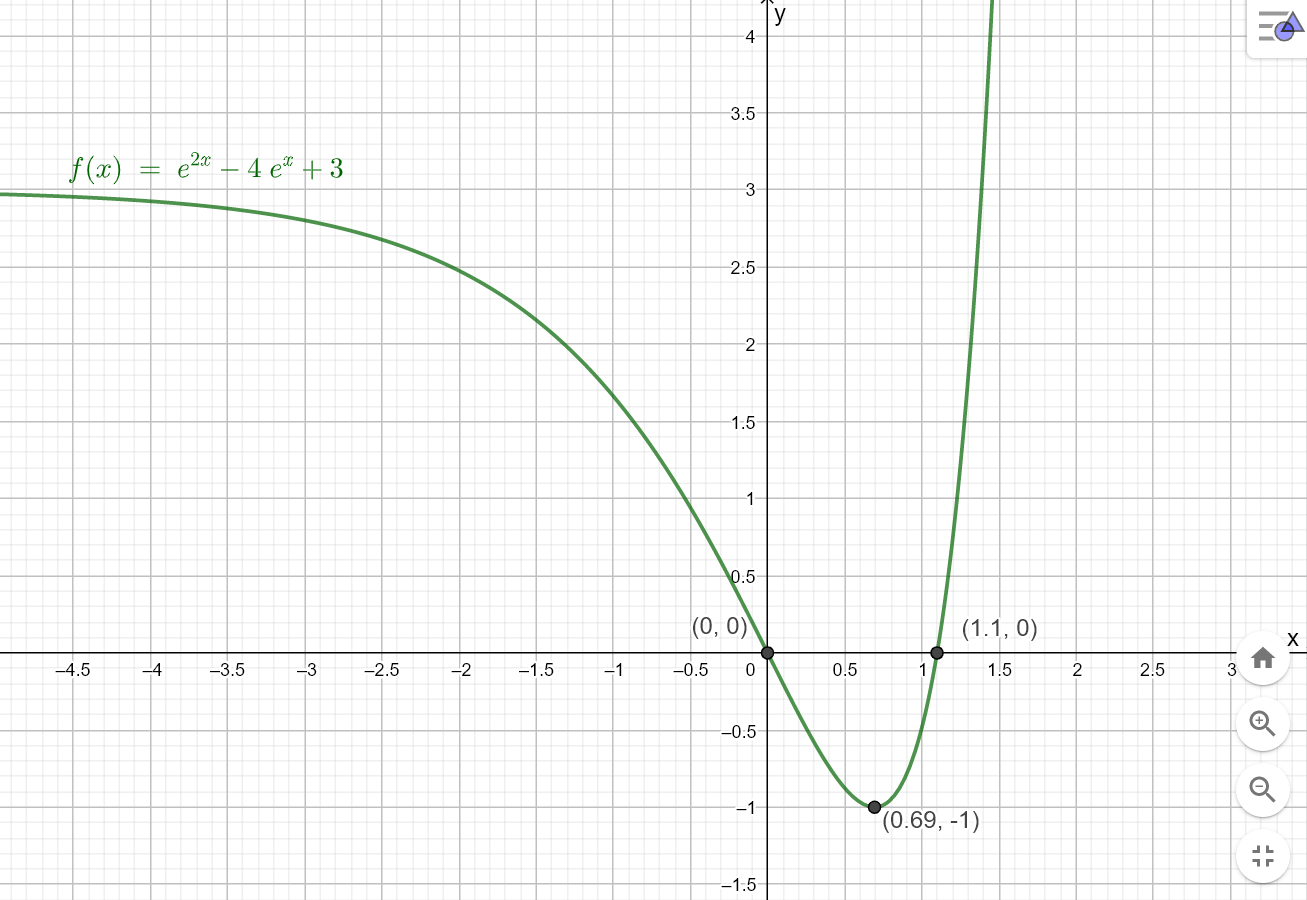
Du må tegne for hånd. Bruk nullpunktene og bunnpunktet fra de forrige oppgavene. Du regne noen omtrentlige funksjonsverdier for å få hjelp til å vite hvordan grafen går. I tillegg har vi at: | |||
$\lim\limits_{x \to - \infty} f(x) = 3$ | |||
$\lim\limits_{x \to \infty} f(x) = \infty$ | |||
[[File: R1_V18_del1_6d.png]] | |||
==Oppgave 7== | |||
===a)=== | |||
For alle par av trekanter, har trekantene parvis like store vinkler, og forholdet mellom alle samsvarende sider er det samme. Alle trekantene er derfor formlike. | |||
===b)=== | |||
Vi tar utgangspunkt i trekant ABD. Vinkelsummen i en trekant er 180 grader, altså er $\angle DAB + \angle BDA + \angle ABD = 180^{\circ}$. | |||
Vi har $\angle DAB = \angle ADE$ fordi disse er samsvarende vinkler. Av samme grunn er $\angle ABD = \angle CDB$. | |||
Det vil si at $\angle ADE + \angle BDA + \angle CDB = 180^{\circ}$, og punkt E, D og C ligger derfor på en rett linje. | |||
===c)=== | |||
Alle trekantene er rettvinklede (gitt i oppgave a). Vi har $\angle E=90^{\circ}$ og $\angle C=90^{\circ}$. | |||
Vi har allerede vist at $\angle ADE$ og $\angle DAB$ er samsvarende, og dermed like store vinkler. $\angle CDB$ og $\angle ABD$ er også samsvarende, og dermed like store vinkler. | |||
Dette gir oss $\angle EAD + \angle ADE = \angle EAD + \angle DAB = \angle A = 90^{\circ}$. På samme måte er $\angle DBC + \angle CDB = \angle DBC + \angle ABD = \angle B = 90^{\circ}$. | |||
Alle vinklene i firkanten er rettvinklede, og firkanten er derfor et rektangel (eventuelt et kvadrat, som er et spesialtilfelle av rektangel). | |||
Vi må se på lengden av sidene for å se at Pytagoras' setning gjelder. I et rektangel er sidene parvis like lange, derfor er $EC = AB$, det vil si $ED+DC = AB$, altså $a^2+b^2 = c^2$. | |||
a og b er katetene i den rettvinklede trekanten i starten av oppgaven, og c er hypotenusen. Vi har vist at $a^2+b^2 = c^2$, altså gjelder Pytagoras' setning. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
Sirkelen har to sentralvinkler, $u$ og $v=360^{\circ}-u$. Periferivinkelen $\angle DCB$ spenner over samme buelengde som sentralvinkelen $v$, og er derfor (ifølge periferivinkelsetningen) halvparten så stor. | |||
$\angle DCB = \frac{v}{2} = \frac{360^{\circ}-u}{2} = 180^{\circ}-\frac{1}{2}u$ | |||
===b)=== | |||
Periferivinklene $\angle BAD$ og $\angle DCB$ spenner til sammen over samme bue som sentralvinklene $u$ og $v$ til sammen. Summen av de to periferivinklene er da halvparten av summen til de to sentralvinklene. | |||
$\angle BAD + \angle DCB = \frac{u+v}{2} = \frac{360^{\circ}}{2} = 180^{\circ}$ | |||
Periferivinklene $\angle CBA$ og $\angle ADC$ spenner til sammen over hele sirkelens omkrets, slik som en sentralvinkel på $360^{\circ}$ også gjør. Summen av disse periferivinklene er derfor halvparten av en sentralvinkel på $360^{\circ}$ | |||
$ \angle CBA + \angle ADC = \frac{360^{\circ}}{2}=180^{\circ}$. | |||
Vi har vist at $\angle BAD + \angle DCB = \angle CBA + \angle ADC = 180^{\circ}$ | |||
==Oppgave 2== | |||
Siste sideversjon per 9. mai 2021 kl. 11:18
Diskusjon av denne oppgaven på matteprat
Løsningsforslag (pdf) (open source, meld fra om forbedringer eller feil her)
Løsningsforslag av LektorNilsen (pdf)
Løsning som video av Lektor Håkon Raustøl
Løsning del 1 som video av Lainz
Løsning del 2 som video av Lainz
DEL 1
Oppgave 1
a)
$f(x)=x^4-x+2$
$f'(x)=4x^3-1$
b)
$g(x)=x^3\cdot ln(x)$
$g'(x)=3x^2\cdot ln(x) + x^3 \cdot \frac{1}{x} = 3x^2ln(x)+x^2$
c)
$h(x)=e^{2x^2+x}$
$h'(x)=(4x+1)e^{2x^2+x}$
Oppgave 2
a)
$\frac{1}{2x-2}+\frac{2}{x-3}-\frac{x-2}{x^2-4x+3} \\ = \frac{1\cdot \color{blue}{(x-3)}}{2(x-1)\color{blue}{(x-3)}}+\frac{2\cdot \color{red}{2(x-1)}}{\color{red}{2(x-1)}(x-3)}-\frac{\color{orange}{2}(x-2)}{\color{orange}{2}(x-1)(x-3)} \\ =\frac{ (x-3) + (4x-4) - (2x-4)}{2(x-1)(x-3)} \\ = \frac{x+4x-2x -3-4+4}{2(x-1)(x-3)} \\ = \frac{3x-3}{2(x-1)(x-3)} \\ = \frac{3(x-1)}{2(x-1)(x-3)} \\ = \frac{3}{2(x-3)} \\ = \frac{3}{2x-6}$
b)
$2ln(x\cdot y^3)-\frac{1}{2}ln(\frac{x^4}{y^2}) \\ = 2(ln(x)+ln(y^3))-\frac{1}{2}(ln(x^4)-ln(y^2)) \\= 2(ln(x)+3ln(y))-\frac{1}{2}(4ln(x)-2ln(y)) \\= 2ln(x)+6ln(y)-2ln(x)+ln(y) \\= 7ln(y)$
Oppgave 3
Vi har punktene A(-2,-1), B(-1, -3), C(3, -1) og D(t,t^2+2) der $t\in R$.
a)
$\vec{AB} = [-1-(-2), -3-(-1)] = [1, -2]$
$\vec{BC} = [3-(-1), -1-(-3)] = [4, 2]$
b)
$[1,-2]\cdot[4,2] = 1\cdot 4 + (-2)\cdot 2 = 4-4 = 0$
Skalarproduktet av $\vec{AB}$ og $\vec{BC}$ er 0, og vi har derfor $\vec{AB}\perp\vec{BC}$
c)
$\vec{CD}=[t-3, t^2+2-(-1)] = [t-3, t^2+3]$
Dersom $\vec{CD}\| \vec{AB}$, så er $\vec{CD} = k\cdot\vec{AB}$
$[t-3,t^2+3]=k\cdot[1,-2]$
Vi får likningssettet:
$I \quad t-3 = k$
$II \quad t^2+3=-2k$
$II \quad t^2+3 = -2 (t-3) \\ \quad t^2 + 3 = -2t+6 \\ \quad t^2 + 2t -3 = 0 \\ \quad (t+3)(t-1) = 0 \\ \quad t = -3 \vee t = 1$
$\vec{CD}\| \vec{AB}$ når $ t = -3 \vee t = 1$.
Oppgave 4
Vi har $f(x)=x^3+k\cdot x + 12$
a)
Dersom $f(x):(x-1)$ skal gå opp, er x=1 et nullpunkt.
$f(1)=0 \\ 1^3+k\cdot 1 + 12 = 0 \\ k+13 = 0 \\ k=-13$
b)
Vi har nå $f(x)=x^3-13x+12$
Utfører polynomdivisjonen:
$f(x)=(x^2+x-12)(x-1) = (x-3)(x-1)(x+4)$
c)
$\frac{x^2+x-12}{x-1} \geq 0 \\ \frac{(x-3)(x+4)}{x-1} \geq 0$
$\frac{x^2+x-12}{x-1} \geq 0$ nå $x\in [-4,1]\cup [3,\rightarrow \rangle$
Oppgave 5
D = defekt
a)
$P(A \cap D) = 0,40 \cdot 0,03 = 0,012 = 1,2 \%$
Sannsynligheten for at laderen kommer fra leverandør A og er defekt, er 1,2%.
b)
$P(D)=P(D|A)\cdot P(A) + P(D|B)\cdot P(B) \\= 0,03\cdot 0,40 + 0,02 \cdot 0,60 = 0,012 + 0,012 = 0,024$
$P(A | D) = \frac{P(A) \cdot P(D|A)}{P(D)} = \frac{0,40 \cdot 0,03}{0,024} = \frac{0,012}{0,024} = 0,5 = 50\%$
Sannsynligheten for at en lader som er defekt, kommer fra leverandør A, er 50%.
Oppgave 6
Vi har $f(x)=e^{2x}-4e^x+3$
a)
$f(x)=0 \\ e^{2x}-4e^x+3 = 0 \\ \text{Setter} \,u = e^x \\ u^2 - 4u + 3 = 0 \\ (u-1)(u-3)=0 \\ u= 1 \vee u = 3 \\ e^x = 1 \vee e^x = 3 \\ x = ln 1 \vee x = ln 3 \\ x = 0 \vee x \approx 1,10 $
Nullpunktene til f er (0,0) og (1.10, 0).
b)
$f'(x)= 2e^{2x}-4e^x$
$f'(x)=0 \\ 2e^{2x}-4e^x = 0 \\ 2e^x(e^x-2)\\ 2e^x = 0 \vee e^x = 2 \\ \xcancel{x = ln 0} \vee x = ln 2 \\ x = ln 2 \approx 0,69$
Forkaster $x = ln 0$ da $ln 0 $ ikke er definert.
Finner funksjonsverdien i x = ln 2.
$f(ln 2) = e^{2(ln2)}-4e^{ln2} + 3 = e^{ln2^2}-4\cdot 2 + 3 = 4-8+3 = -1$
Grafen til f har et bunnpunkt i (0.69, -1).
c)
$f' '(x)=4e^{2x}-4e^x = 4e^x(e^x-1)$
$f' '(x)=0 \\ 4e^x(e^x-1) = 0 \\ 4e^x = 0 \vee e^x = 1 \\ \xcancel{x = ln0} \vee x=ln1 \\ x=0$
Finner funksjonsverdien i x = 0.
$f(0)=e^{2\cdot 0}-4e^0+3 = 1-4+3 = 0$
Grafen til f har et vendepunkt i (0,0).
d)
Du må tegne for hånd. Bruk nullpunktene og bunnpunktet fra de forrige oppgavene. Du regne noen omtrentlige funksjonsverdier for å få hjelp til å vite hvordan grafen går. I tillegg har vi at:
$\lim\limits_{x \to - \infty} f(x) = 3$
$\lim\limits_{x \to \infty} f(x) = \infty$
Oppgave 7
a)
For alle par av trekanter, har trekantene parvis like store vinkler, og forholdet mellom alle samsvarende sider er det samme. Alle trekantene er derfor formlike.
b)
Vi tar utgangspunkt i trekant ABD. Vinkelsummen i en trekant er 180 grader, altså er $\angle DAB + \angle BDA + \angle ABD = 180^{\circ}$.
Vi har $\angle DAB = \angle ADE$ fordi disse er samsvarende vinkler. Av samme grunn er $\angle ABD = \angle CDB$.
Det vil si at $\angle ADE + \angle BDA + \angle CDB = 180^{\circ}$, og punkt E, D og C ligger derfor på en rett linje.
c)
Alle trekantene er rettvinklede (gitt i oppgave a). Vi har $\angle E=90^{\circ}$ og $\angle C=90^{\circ}$.
Vi har allerede vist at $\angle ADE$ og $\angle DAB$ er samsvarende, og dermed like store vinkler. $\angle CDB$ og $\angle ABD$ er også samsvarende, og dermed like store vinkler.
Dette gir oss $\angle EAD + \angle ADE = \angle EAD + \angle DAB = \angle A = 90^{\circ}$. På samme måte er $\angle DBC + \angle CDB = \angle DBC + \angle ABD = \angle B = 90^{\circ}$.
Alle vinklene i firkanten er rettvinklede, og firkanten er derfor et rektangel (eventuelt et kvadrat, som er et spesialtilfelle av rektangel).
Vi må se på lengden av sidene for å se at Pytagoras' setning gjelder. I et rektangel er sidene parvis like lange, derfor er $EC = AB$, det vil si $ED+DC = AB$, altså $a^2+b^2 = c^2$.
a og b er katetene i den rettvinklede trekanten i starten av oppgaven, og c er hypotenusen. Vi har vist at $a^2+b^2 = c^2$, altså gjelder Pytagoras' setning.
DEL 2
Oppgave 1
a)
Sirkelen har to sentralvinkler, $u$ og $v=360^{\circ}-u$. Periferivinkelen $\angle DCB$ spenner over samme buelengde som sentralvinkelen $v$, og er derfor (ifølge periferivinkelsetningen) halvparten så stor.
$\angle DCB = \frac{v}{2} = \frac{360^{\circ}-u}{2} = 180^{\circ}-\frac{1}{2}u$
b)
Periferivinklene $\angle BAD$ og $\angle DCB$ spenner til sammen over samme bue som sentralvinklene $u$ og $v$ til sammen. Summen av de to periferivinklene er da halvparten av summen til de to sentralvinklene.
$\angle BAD + \angle DCB = \frac{u+v}{2} = \frac{360^{\circ}}{2} = 180^{\circ}$
Periferivinklene $\angle CBA$ og $\angle ADC$ spenner til sammen over hele sirkelens omkrets, slik som en sentralvinkel på $360^{\circ}$ også gjør. Summen av disse periferivinklene er derfor halvparten av en sentralvinkel på $360^{\circ}$
$ \angle CBA + \angle ADC = \frac{360^{\circ}}{2}=180^{\circ}$.
Vi har vist at $\angle BAD + \angle DCB = \angle CBA + \angle ADC = 180^{\circ}$