Cosinussetningen: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| (7 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
I en trekant med vinkler A, B og C og sider a, b og c (a motstående til A osv.) er <br> | |||
[[Bilde:costre.gif]]<br> | |||
<div style="padding: 1em; border: 1px blue; background-color: #C9EFF8;"> | |||
< | <math>a^2 =b^2+ c^2 - 2bc \cdot cosA </math><br> | ||
eller | eller<br> | ||
< | <math>b^2 =a^2+ c^2 - 2ac \cdot cosB </math><br> | ||
eller<br> | |||
<math>c^2 =a^2+ b^2 - 2ab \cdot cosC </math><br> | |||
</div> | |||
Setningen kalles også den utvidede pytagoreiske læresetning.<br> | |||
Dersom man kjenner alle tre sidene i en trekant kan man bruke cosinussetningen til å finne vinklene. Man kan også bruke cosinussetningen til å finne en side, dersom man kjenner to sider og motstående vinkel til den ukjente siden. | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel :''' | |||
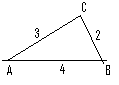
<br> En trekant har sider med lengde 4,3 og 2. Hva er vinklene i trekanten? Trekanten kan se slik ut:<br>[[Bilde:cos1.PNG]]<br> | |||
<math>a^2 =b^2+ c^2 - 2bc \cdot cosA \Rightarrow Cos A = \frac{a^2 -b^2- c^2}{-2bc} = | |||
\frac{4-9-16}{-2\cdot 3 \cdot 4}= \frac{21}{24}\Rightarrow A = 29 ^\circ</math> | |||
<br><br> | |||
<math>b^2 =a^2+ c^2 - 2ac \cdot cosB \Rightarrow Cos B = \frac{b^2 -a^2- c^2}{-2ac} = | |||
\frac{9-4-16}{-2\cdot 2 \cdot 4}= \frac{11}{16}\Rightarrow B = 46,6 ^\circ</math> | |||
</blockquote> | |||
[[Bevis for cosinussetningen]] | [[Bevis for cosinussetningen]] | ||
| Linje 21: | Linje 36: | ||
[[Category:Trigonometri]] | [[Category:Trigonometri]] | ||
[[Category:1T]][[Category:Ped]] | [[Category:1T]][[Category:Ped]] | ||
Siste sideversjon per 15. apr. 2021 kl. 06:30
I en trekant med vinkler A, B og C og sider a, b og c (a motstående til A osv.) er
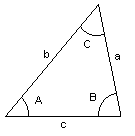
<math>a^2 =b^2+ c^2 - 2bc \cdot cosA </math>
eller
<math>b^2 =a^2+ c^2 - 2ac \cdot cosB </math>
eller
<math>c^2 =a^2+ b^2 - 2ab \cdot cosC </math>
Setningen kalles også den utvidede pytagoreiske læresetning.
Dersom man kjenner alle tre sidene i en trekant kan man bruke cosinussetningen til å finne vinklene. Man kan også bruke cosinussetningen til å finne en side, dersom man kjenner to sider og motstående vinkel til den ukjente siden.
Eksempel :
En trekant har sider med lengde 4,3 og 2. Hva er vinklene i trekanten? Trekanten kan se slik ut:
<math>a^2 =b^2+ c^2 - 2bc \cdot cosA \Rightarrow Cos A = \frac{a^2 -b^2- c^2}{-2bc} = \frac{4-9-16}{-2\cdot 3 \cdot 4}= \frac{21}{24}\Rightarrow A = 29 ^\circ</math>
<math>b^2 =a^2+ c^2 - 2ac \cdot cosB \Rightarrow Cos B = \frac{b^2 -a^2- c^2}{-2ac} = \frac{9-4-16}{-2\cdot 2 \cdot 4}= \frac{11}{16}\Rightarrow B = 46,6 ^\circ</math>