Figurer i planet: Forskjell mellom sideversjoner
| (98 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 26: | Linje 26: | ||
<p></p> | <p></p> | ||
[[Bilde: | [[Bilde:Paralinjer_1.png]]<p></p> | ||
| Linje 33: | Linje 33: | ||
== Vinkler == | == Vinkler == | ||
Rette linjer som ikke er parallelle vil før eller siden krysse hverandre (i planet). Da vil de danne en vinkel. Symbolet for en vinkel er . Dette tegnet må ikke forveksles med < som betyr "mindre enn". Vinkelen ABC kan skrives slik: ABC, eller noen ganger bare som B. Vinkelen kan se slik ut: | Rette linjer som ikke er parallelle vil før eller siden krysse hverandre (i planet). Da vil de danne en vinkel. Symbolet for en vinkel er<math>\angle </math> . Dette tegnet må ikke forveksles med < som betyr "mindre enn". Vinkelen ABC kan skrives slik: ABC, eller noen ganger bare som B. Vinkelen kan se slik ut: | ||
<p></p> | |||
[[Bilde:Vink_1.png]]<p></p> | |||
| Linje 39: | Linje 42: | ||
En vinkel består av to vinkelbein og et toppunkt. Toppunktet er der hvor vinkelbeina møtes (eller krysser hverandre). AB og BC er vinkelbein og B er toppunktet. I denne figuren kunne vi kalt vinkelen for B, men vi skal senere se at vi av og til må kalle vinklene med vinkelbein, altså ABC, for å unngå missforståelser. | En vinkel består av to vinkelbein og et toppunkt. Toppunktet er der hvor vinkelbeina møtes (eller krysser hverandre). AB og BC er vinkelbein og B er toppunktet. I denne figuren kunne vi kalt vinkelen for B, men vi skal senere se at vi av og til må kalle vinklene med vinkelbein, altså ABC, for å unngå missforståelser. | ||
Lengde måles i meter og tid i sekunder eller timer. Vinkler måles i grader. Dette har ingen ting med temperatur å gjøre, men symbolet vi bruker er det samme. 30 grader skrives 30º. En sirkel måler 360°. Gradeskiven din (også kalt transportør) kan du bruke når du tegner eller måler vinkler. Den går vanligvis opp til 180°. | Lengde måles i meter og tid i sekunder eller timer. Vinkler måles i grader. Dette har ingen ting med temperatur å gjøre, men symbolet vi bruker er det samme. 30 grader skrives 30º. En sirkel måler 360°. Gradeskiven din (også kalt transportør) kan du bruke når du tegner eller måler vinkler. Den går vanligvis opp til 180°. | ||
| Linje 45: | Linje 47: | ||
Det er forskjellige navn på forskjellige typer vinkler. Vi skal se på disse. | Det er forskjellige navn på forskjellige typer vinkler. Vi skal se på disse. | ||
Definisjoner: | '''Definisjoner:''' | ||
<p></p> | |||
[[Bilde:Vinkler_1.png]]<p></p> | |||
| Linje 56: | Linje 62: | ||
=== | ===Nabovinkler=== | ||
Summen av to nabovinkler er 180º | Summen av to nabovinkler er 180º | ||
<p></p> | |||
[[Bilde:nabovink_1.png]]<p></p> | |||
===Toppvinkler=== | ===Toppvinkler=== | ||
Når to linjer krysser hverandre dannes det fire vinkler som parvis er like store. | Når to linjer krysser hverandre dannes det fire vinkler som parvis er like store. | ||
<p></p> | |||
[[Bilde:toppvink_1.png]]<p></p> | |||
| Linje 72: | Linje 83: | ||
Vinkler som har forskjellig toppunkt, men et vinkelbein felles, kalles samsvarende vinkler. | Vinkler som har forskjellig toppunkt, men et vinkelbein felles, kalles samsvarende vinkler. | ||
<p></p> | |||
[[Bilde:Samsvar.png]]<p></p> | |||
Dersom man vet, eller kan vise at linjen l er parallell med linjen m er vinkel a lik vinkel b, vinkel c lik vinkel d, osv. | |||
== Speiling & symmetri == | == Speiling & symmetri == | ||
Speiling om en Linje | ===Speiling om en Linje=== | ||
Når du betrakter deg selv i speilet vil du se følgende: Dersom du beveger deg mot speilet, vil speilbildet bevege seg mot deg. Dersom du rygger vil speilbildet trekke seg tilbake. Tenk deg at vi kunne observere dette fra siden, da ville vi ha ditt hode og speilbildet i profil, og speilet ville bare være en strek (fordi vi ser det fra siden). Dette kan se noe slik ut: | Når du betrakter deg selv i speilet vil du se følgende: Dersom du beveger deg mot speilet, vil speilbildet bevege seg mot deg. Dersom du rygger vil speilbildet trekke seg tilbake. Tenk deg at vi kunne observere dette fra siden, da ville vi ha ditt hode og speilbildet i profil, og speilet ville bare være en strek (fordi vi ser det fra siden). Dette kan se noe slik ut: | ||
<p></p> | |||
[[Bilde:Speil_1.png]]<p></p> | |||
Når vi i matematikken skal speile noe om en akse eller linje gjør vi følgende: Vi trekker linjer fra punkt på det objekt som skal speiles. Disse linjene skal stå normalt på linjen man speiler om. Mål avstanden fra punktet på objektet til speilingslinjen. Denne avstanden Legger du så til på andre siden av speilingslinjen. Der merker du av punktet som blir et punkt på speilbildet. Dersom vi har en figur med et punkt A, kaller vi tilsvarende punkt på speilbildet for A'. Dette kan foreksempel se slik ut: | Når vi i matematikken skal speile noe om en akse eller linje gjør vi følgende: Vi trekker linjer fra punkt på det objekt som skal speiles. Disse linjene skal stå normalt på linjen man speiler om. Mål avstanden fra punktet på objektet til speilingslinjen. Denne avstanden Legger du så til på andre siden av speilingslinjen. Der merker du av punktet som blir et punkt på speilbildet. Dersom vi har en figur med et punkt A, kaller vi tilsvarende punkt på speilbildet for A'. Dette kan foreksempel se slik ut: | ||
<p></p> | |||
[[Bilde:Speil_2.png]]<p></p> | |||
| Linje 88: | Linje 105: | ||
Om vi starter med situasjonen til venstre | Om vi starter med situasjonen til venstre | ||
<p></p> | |||
[[Bilde:Speil_4.png]]<p></p> | |||
blir resultatet av speilingen situasjonen til høyre. Dersom figuren vi skal speile ligger delvis over speilingslinjen kan det se slik ut: | |||
<p></p> | |||
[[Bilde:Speil_5.png]]<p></p> | |||
[http://www.matematikk.net/emner/applets/ggbApplet.php?appid=16 speiling om linje] | |||
Symmetriakser | ===Symmetriakser=== | ||
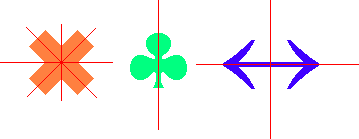
Noen eksempler på symmetriakser er vist nedenfor. Vi observerer at forskjellige former har forskjellig antall symmetriakser. | Noen eksempler på symmetriakser er vist nedenfor. Vi observerer at forskjellige former har forskjellig antall symmetriakser. | ||
<p></p> | |||
[[Bilde:Sym_1.png]]<p></p> | |||
Dersom vi bretter disse figurene langs en symmetriakse, de røde strekene, ser vi at delene på hver side av aksen vil overlappe hverandre fullstendig. | Dersom vi bretter disse figurene langs en symmetriakse, de røde strekene, ser vi at delene på hver side av aksen vil overlappe hverandre fullstendig. | ||
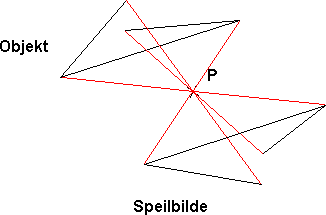
Speiling om et Punkt | ===Speiling om et Punkt=== | ||
Når vi speiler om et punkt trekker vi linjer fra objektet som skal speiles, gjennom punktet. Avstanden fra objektet til punktet er lik avstanden fra punktet til speilbildet. | Når vi speiler om et punkt trekker vi linjer fra objektet som skal speiles, gjennom punktet. Avstanden fra objektet til punktet er lik avstanden fra punktet til speilbildet. | ||
Eks: | Eks: | ||
<p></p> | |||
[[Bilde:Speilpunkt_1.png]]<p></p> | |||
[http://www.matematikk.net/emner/applets/ggbApplet.php?appid=0 speiling om punkt] | |||
== Kongruente Former == | == Kongruente Former == | ||
| Linje 115: | Linje 141: | ||
Geometriske figurer som dekker hverandre helt når vi legger den oppå hverandre kalles for kongruente. Det kan tenkes at vi må rotere figurene for at de skal dekke hverandre. | Geometriske figurer som dekker hverandre helt når vi legger den oppå hverandre kalles for kongruente. Det kan tenkes at vi må rotere figurene for at de skal dekke hverandre. | ||
<p></p> | |||
[[Bilde:kongr_1.png]]<p></p> | |||
| Linje 122: | Linje 150: | ||
En trekant har tre vinkler og tre sidekanter. | En trekant har tre vinkler og tre sidekanter. | ||
[[Bilde:Trekant.png]]<p></p> | |||
<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
Vinkelsummen i en trekant er 180° | |||
A + B + C = 180° | |||
</blockquote> | |||
Arealet av en trekant er | Arealet av en trekant er: | ||
<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
<math>Areal = \frac{Gh}{2} </math> | |||
</blockquote> | |||
| Linje 134: | Linje 171: | ||
Der G er grunnlinja og h er høyden av trekanten. | Der G er grunnlinja og h er høyden av trekanten. | ||
Figuren under viser hvorfor formelen for arealet er slik. | Figuren under viser hvorfor formelen for arealet er slik.<p></p> | ||
[[Bilde:Trekant2.png]]<p></p> | |||
=== Rettvinklet Trekant === | === Rettvinklet Trekant === | ||
| Linje 141: | Linje 178: | ||
En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten. | En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten. | ||
[[Bilde:Rettvinklet.png]]<p></p> | |||
En rett vinkel er 90 grader og markeres som vist i A.<p></p> | |||
Arealet av en rettvinklet trekant er katet ganger katet delt på to. Fordi det ene katetet gir høyden i trekanten, og det andre grunnlinjen. Det er selvsagt mulig å bruke hypotenusen som grunnlinjen, men det vil ogfe føre til noe mer komplisert regning fordi man da må finne høyden fra hypotenusen til motstående vinlel. | |||
=== Likebeint Trekant === | === Likebeint Trekant === | ||
| Linje 147: | Linje 187: | ||
Dersom to av sidene i en trekant er like lange er trekanten likebeint. "Pinnene" på sidene AC og BC markere at disse sidene er like lange. Når to sider i en trekant er like lange medfører det at to vinkler er like store. I dette eksempelet er vinkel A og vinkel B like store. | Dersom to av sidene i en trekant er like lange er trekanten likebeint. "Pinnene" på sidene AC og BC markere at disse sidene er like lange. Når to sider i en trekant er like lange medfører det at to vinkler er like store. I dette eksempelet er vinkel A og vinkel B like store. | ||
[[Bilde:Likebeint.png]]<p></p> | |||
=== Likesidet Trekant === | === Likesidet Trekant === | ||
| Linje 154: | Linje 194: | ||
I en likesidet trekant er alle sidene like lange og alle vinklene er 60° | I en likesidet trekant er alle sidene like lange og alle vinklene er 60° | ||
[[Bilde:Likesidet.png]]<p></p> | |||
== Pythagoras == | |||
<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
Pythagoras setning kan i hovedsak brukes til tre ting; | |||
<p></p>'''1. finne lengden av hypotenusen i en rettvinklet trekant''' | |||
<p></p>'''2. finne lengden av et katet i en rettvinklet trekant''' | |||
<p></p>'''3. finne ut om en trekant er rettvinklet''' <p></p><p></p> | |||
</blockquote> | |||
I en rettvinklet trekant er arealet av kvadratet på hypotenusen lik summen av arealet til kvadratene på katetene. | |||
[[Bilde:Pyt.png]]<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
<math>c^2 = a^2 + b^2 </math><p></p> | |||
Setningen gjelder kun for rettvinklede trekanter. | |||
</blockquote> | |||
<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel 1:''' (hypotenus og et katet kjent)<p></p> | |||
[[Bilde:Pyt31.png]]<p></p> | |||
Hva er lengden av AC? | Hva er lengden av AC? | ||
<p></p> <math>(AB)^2 +(AC)^2 = (BC)^2 \\(5cm)^2 + (AC)^2 = (10cm)^2 \\25cm^2 + (AC)^2 = 100cm^2 \\AC = \sqrt {75cm^2} = 8,7 cm </math> | |||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel 2:''' (begge kateter kjent) | |||
<p></p> | |||
[[Bilde:Pyt32-.png]]<p></p> | |||
Hva er lengden av BC? | Hva er lengden av BC? | ||
<p></p> <math>(AB)^2 +(AC)^2 = (BC)^2 \\(3cm)^2 + (4cm)^2 = (BC)^2 \\9cm^2 + 16cm^2 = (BC)^2 \\BC = \sqrt {25cm^2} = 5 cm </math> | |||
</blockquote> | |||
I en rettvinklet trekant der vinklene er 30° ,60° og 90° vil alltid hypotenusen være dobbelt så lang som det korteste katetet. Det korteste katetet vil alltid være det motstående til vinkelen på 30°. Dette medfører blant annet at vi er i stand til å finne to sider i en rettvinklet trekant, når betingelsene er som over og vi kjenner en side. | I en rettvinklet trekant der vinklene er 30° ,60° og 90° vil alltid hypotenusen være dobbelt så lang som det korteste katetet. Det korteste katetet vil alltid være det motstående til vinkelen på 30°. Dette medfører blant annet at vi er i stand til å finne to sider i en rettvinklet trekant, når betingelsene er som over og vi kjenner en side. | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel 3:'''(spesialtilfelle)<p></p> | |||
[[Bilde:Pyt33.png]]<p></p> | |||
Finn AC og BC. | Finn AC og BC. | ||
| Linje 194: | Linje 266: | ||
Siden vi har 30°,60° og 90° i trekanten vet vi at BC = 2 AC. La oss sette AC = x | Siden vi har 30°,60° og 90° i trekanten vet vi at BC = 2 AC. La oss sette AC = x | ||
<p></p> <math>(AB)^2 +(AC)^2 = (BC)^2 \\(8cm)^2 + x^2 = (2x)^2 \\64cm^2 + x^2 = 4x^2 \\3x^2 = 64cm^2\\x^2 = 21,3cm^2\\x=4,6cm </math> | |||
<p></p> AC = 4,6 cm og BC = 9,2 cm. | |||
</blockquote> | |||
Man kan bruke Pytagoras til å sjekke om en gitt trekant er rettvinklet. Man sjekker om kvadratet utspendt av den lengste siden er lik summen av kvadratene utspendt av de to korteste. | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
'''Eksempel 4:'''(spesialtilfelle)<p></p> | |||
I en trekant er siden 3 meter, 4 meter og 5,5 meter. Er trekanten rettvinklet?<p></p> | |||
'''LØSNING''':<p></p> | |||
Dersom trekanten er rettvinklet må den lengste siden være hypotenusen. Det betyr at <math>3^2 + 4^2 = 25</math> må være lik <math>5,5^2</math>. Det er ikke tilfellet, derfor er trekanten ikke rettvinklet. | |||
</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A94%2BA95%2BA96%2BA97%2BA98%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
== Firkanter == | == Firkanter == | ||
| Linje 206: | Linje 290: | ||
Et kvadrat er en firkant hvor alle sidene er like lange og alle vinklene er 90°. Diagonalene er markert med røde linjer. En diagonal er en rett linje som går fra et hjørne i firkanten til motstående hjørne. | Et kvadrat er en firkant hvor alle sidene er like lange og alle vinklene er 90°. Diagonalene er markert med røde linjer. En diagonal er en rett linje som går fra et hjørne i firkanten til motstående hjørne. Et kvadrat er et spesialtilfelle av et rektangel. | ||
<p></p> | |||
[[Bilde:kvadrat_1.png]]<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
Arealet av kvadratet er: A = a | Arealet av kvadratet er:<p></p> | ||
<math> A = a \cdot a = a^2</math> | |||
</blockquote> | |||
Omkretsen er: O = a + a + a + a = 4a. | <blockquote style="padding: 1em; border: 3px dotted blue;"> | ||
Omkretsen av kvadratet er:<p></p> | |||
<math> O = a + a + a + a = 4a.</math></blockquote> | |||
<p></p> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A34%2BA35%2BA36%2BA37%2BA38%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
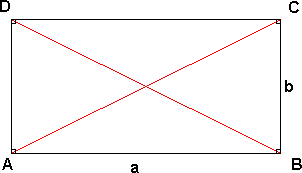
===Rektangel=== | ===Rektangel=== | ||
<p></p> | |||
[[Bilde:rektangel_1.png]]<p></p> | |||
Et rektangel er en firkant der sidene er parvis like lange. Vinklene er 90°. | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
Arealet av rektangelet er: A = ab | Arealet av rektangelet er: A = ab | ||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
Omkretsen er: O = a + a + b + b = 2a + 2b.</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=A2F%2BA30%2BA31%2BA32%2BA33%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
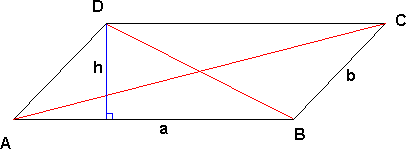
===Parallellogram=== | ===Parallellogram=== | ||
<p></p> | |||
[[Bilde:parallellogram_1.png]]<p></p> | |||
Et parallellogram er en firkant hvor sidene er parvis parallelle. | Et parallellogram er en firkant hvor sidene er parvis parallelle. | ||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
'''Areal:''' | |||
<p></p> A = ah <p></p></blockquote> | |||
<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
'''Omkrets''' | |||
<p></p> | |||
O = 2(a+b) | |||
<p></p></blockquote> | |||
===Rombe=== | ===Rombe=== | ||
<p></p> | |||
[[Bilde:rombe_1.png]]<p></p> | |||
En rombe er en firkant der alle sidene er like lange og parvis parallelle. En rombe er et spesialtilfelle av et parallellogram. | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
'''Areal:''' | |||
<p></p> A = ah <p></p></blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
'''Omkrets:''' | |||
<p></p> | |||
Da alle sidene er like lange er<p></p> | |||
a = b = c = d | |||
<p></p> | |||
Da blir | |||
O = 4a | |||
</blockquote> | |||
[http://www.matematikk.net/ressurser/oppgaver/kari/vis_oppgaver.php?q=B54%2BB55%2BB56%2BB57%2BB58%7Ctimer_off%7Cshow_all%7Cnq%5B5%5D%7Ccat%5B35%5D%7Cdiff%5B0%5D%26quser_submit_step3 Test deg selv] | |||
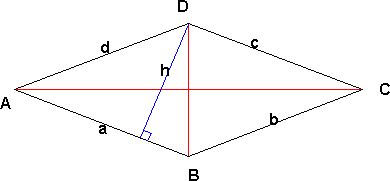
===Trapes=== | ===Trapes=== | ||
<p></p> | |||
[[Bilde:trapes_1.png]]<p></p> | |||
I et trapes er to av sidene parallelle | I et trapes er to av sidene parallelle. [[ Trapes ]] | ||
'''Areal:''' | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
<p></p> | |||
<math> A= \frac{h \cdot (AB+CD)}{2}</math> | |||
</blockquote> | |||
'''Omkrets:'''<p></p> | |||
<blockquote style="padding: 1em; border: 3px dotted blue;"> | |||
O = AB + BC + CD + DA | |||
</blockquote> | |||
<blockquote style="padding: 1em; border: 3px dotted red;"> | |||
<p></p> | |||
</blockquote> | |||
---- | |||
[[Ungdomstrinn Hovedside | Tilbake til Ungdomstrinn Hovedside]]<p></p> | |||
[[Hovedside| Tilbake til hovedside]] | |||
[[Category:Geometri]] | |||
[[Category:U - trinn]] [[Category:Ped]] | |||
Siste sideversjon per 27. aug. 2020 kl. 04:17
Punkt
Et punkt markeres med et kryss. Punktet P kan markeres slik:
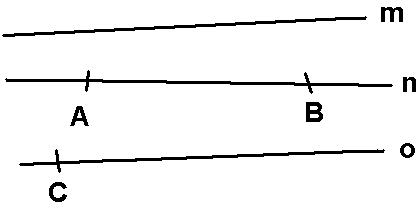
Linjer
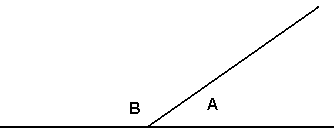
Linjen m har uendelig utstrekning, den fortsetter i begge retninger. Linjestykket AB ligger på linjen n. Linjen n er uendelig lang, men linjestykket AB har en målbar lengde. Linjen o er uendelig lang, det er også linjestrålen som slutter i C.
Dette kan markeres slik:
Parallelle Linjer
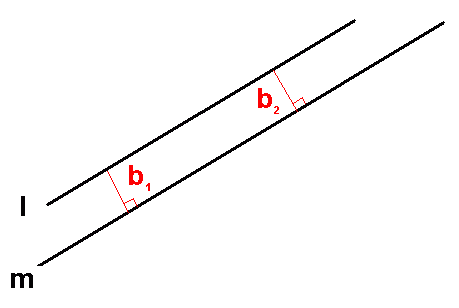
Dersom linjen l er parallell med linjen m betyr det at disse to linjene aldri vil krysse hverandre. Vi skriver det slik:
m || n
Linjene kan se slik ut:
Dersom linjene er parallelle betyr det at avstanden mellom dem er den samme hele veien. Det betyr at avstanden b1 er den samme som b2.
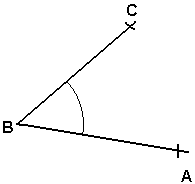
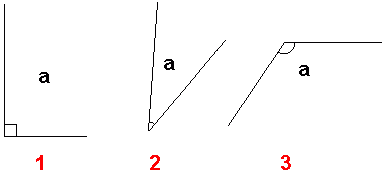
Vinkler
Rette linjer som ikke er parallelle vil før eller siden krysse hverandre (i planet). Da vil de danne en vinkel. Symbolet for en vinkel er<math>\angle </math> . Dette tegnet må ikke forveksles med < som betyr "mindre enn". Vinkelen ABC kan skrives slik: ABC, eller noen ganger bare som B. Vinkelen kan se slik ut:
En vinkel består av to vinkelbein og et toppunkt. Toppunktet er der hvor vinkelbeina møtes (eller krysser hverandre). AB og BC er vinkelbein og B er toppunktet. I denne figuren kunne vi kalt vinkelen for B, men vi skal senere se at vi av og til må kalle vinklene med vinkelbein, altså ABC, for å unngå missforståelser.
Lengde måles i meter og tid i sekunder eller timer. Vinkler måles i grader. Dette har ingen ting med temperatur å gjøre, men symbolet vi bruker er det samme. 30 grader skrives 30º. En sirkel måler 360°. Gradeskiven din (også kalt transportør) kan du bruke når du tegner eller måler vinkler. Den går vanligvis opp til 180°.
Det er forskjellige navn på forskjellige typer vinkler. Vi skal se på disse.
Definisjoner:
1: Rett vinkel, er en vinkel som er 90°. Kalles også for 90 graders vinkel.
2: Spiss vinkel, er en vinkel som er mindre enn 90º.
3: Stomp vinkel, er en vinkel som er større enn 90º.
Nabovinkler
Summen av to nabovinkler er 180º
Toppvinkler
Når to linjer krysser hverandre dannes det fire vinkler som parvis er like store.
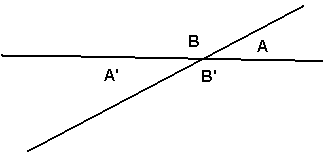
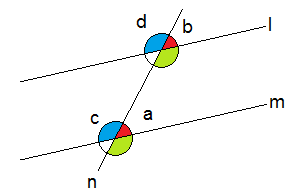
Samsvarende vinkler
Vinkler som har forskjellig toppunkt, men et vinkelbein felles, kalles samsvarende vinkler.
Dersom man vet, eller kan vise at linjen l er parallell med linjen m er vinkel a lik vinkel b, vinkel c lik vinkel d, osv.
Speiling & symmetri
Speiling om en Linje
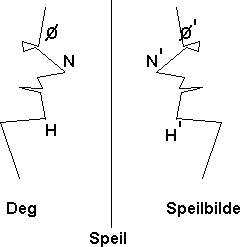
Når du betrakter deg selv i speilet vil du se følgende: Dersom du beveger deg mot speilet, vil speilbildet bevege seg mot deg. Dersom du rygger vil speilbildet trekke seg tilbake. Tenk deg at vi kunne observere dette fra siden, da ville vi ha ditt hode og speilbildet i profil, og speilet ville bare være en strek (fordi vi ser det fra siden). Dette kan se noe slik ut:
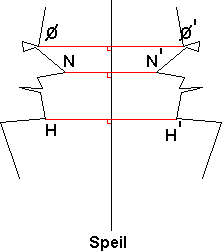
Når vi i matematikken skal speile noe om en akse eller linje gjør vi følgende: Vi trekker linjer fra punkt på det objekt som skal speiles. Disse linjene skal stå normalt på linjen man speiler om. Mål avstanden fra punktet på objektet til speilingslinjen. Denne avstanden Legger du så til på andre siden av speilingslinjen. Der merker du av punktet som blir et punkt på speilbildet. Dersom vi har en figur med et punkt A, kaller vi tilsvarende punkt på speilbildet for A'. Dette kan foreksempel se slik ut:
Legg merke till at avstanden fra Ø til speil er lik avstanden fra speil til Ø', avstanden fra N til speil er lik avstanden fra speil til N', osv.
Om vi starter med situasjonen til venstre
blir resultatet av speilingen situasjonen til høyre. Dersom figuren vi skal speile ligger delvis over speilingslinjen kan det se slik ut:
Symmetriakser
Noen eksempler på symmetriakser er vist nedenfor. Vi observerer at forskjellige former har forskjellig antall symmetriakser.
Dersom vi bretter disse figurene langs en symmetriakse, de røde strekene, ser vi at delene på hver side av aksen vil overlappe hverandre fullstendig.
Speiling om et Punkt
Når vi speiler om et punkt trekker vi linjer fra objektet som skal speiles, gjennom punktet. Avstanden fra objektet til punktet er lik avstanden fra punktet til speilbildet.
Eks:
Kongruente Former
Geometriske figurer som dekker hverandre helt når vi legger den oppå hverandre kalles for kongruente. Det kan tenkes at vi må rotere figurene for at de skal dekke hverandre.
Dersom figur B roteres 90º med klokka, ser vi at figur A og B dekker hverandre helt. A og B er kongruente figurer.
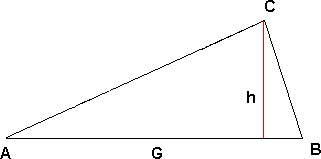
Trekanter
En trekant har tre vinkler og tre sidekanter.
Vinkelsummen i en trekant er 180° A + B + C = 180°
Arealet av en trekant er:
<math>Areal = \frac{Gh}{2} </math>
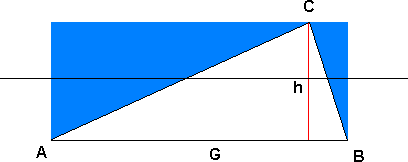
Der G er grunnlinja og h er høyden av trekanten.
Figuren under viser hvorfor formelen for arealet er slik.
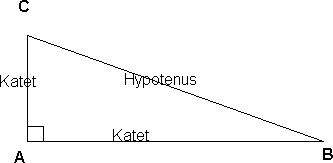
Rettvinklet Trekant
En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten.
En rett vinkel er 90 grader og markeres som vist i A.
Arealet av en rettvinklet trekant er katet ganger katet delt på to. Fordi det ene katetet gir høyden i trekanten, og det andre grunnlinjen. Det er selvsagt mulig å bruke hypotenusen som grunnlinjen, men det vil ogfe føre til noe mer komplisert regning fordi man da må finne høyden fra hypotenusen til motstående vinlel.
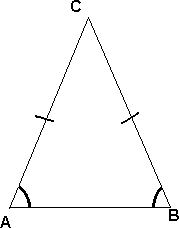
Likebeint Trekant
Dersom to av sidene i en trekant er like lange er trekanten likebeint. "Pinnene" på sidene AC og BC markere at disse sidene er like lange. Når to sider i en trekant er like lange medfører det at to vinkler er like store. I dette eksempelet er vinkel A og vinkel B like store.
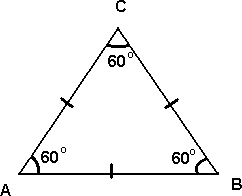
Likesidet Trekant
I en likesidet trekant er alle sidene like lange og alle vinklene er 60°
Pythagoras
Pythagoras setning kan i hovedsak brukes til tre ting;
1. finne lengden av hypotenusen i en rettvinklet trekant
2. finne lengden av et katet i en rettvinklet trekant
3. finne ut om en trekant er rettvinklet
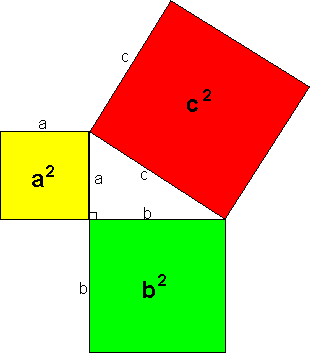
I en rettvinklet trekant er arealet av kvadratet på hypotenusen lik summen av arealet til kvadratene på katetene.
<math>c^2 = a^2 + b^2 </math>
Setningen gjelder kun for rettvinklede trekanter.
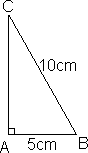
Eksempel 1: (hypotenus og et katet kjent)
Hva er lengden av AC?
<math>(AB)^2 +(AC)^2 = (BC)^2 \\(5cm)^2 + (AC)^2 = (10cm)^2 \\25cm^2 + (AC)^2 = 100cm^2 \\AC = \sqrt {75cm^2} = 8,7 cm </math>
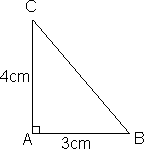
Eksempel 2: (begge kateter kjent)
Hva er lengden av BC?
<math>(AB)^2 +(AC)^2 = (BC)^2 \\(3cm)^2 + (4cm)^2 = (BC)^2 \\9cm^2 + 16cm^2 = (BC)^2 \\BC = \sqrt {25cm^2} = 5 cm </math>
I en rettvinklet trekant der vinklene er 30° ,60° og 90° vil alltid hypotenusen være dobbelt så lang som det korteste katetet. Det korteste katetet vil alltid være det motstående til vinkelen på 30°. Dette medfører blant annet at vi er i stand til å finne to sider i en rettvinklet trekant, når betingelsene er som over og vi kjenner en side.
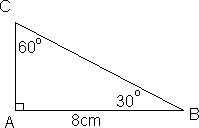
Eksempel 3:(spesialtilfelle)
Finn AC og BC.
Siden vi har 30°,60° og 90° i trekanten vet vi at BC = 2 AC. La oss sette AC = x
<math>(AB)^2 +(AC)^2 = (BC)^2 \\(8cm)^2 + x^2 = (2x)^2 \\64cm^2 + x^2 = 4x^2 \\3x^2 = 64cm^2\\x^2 = 21,3cm^2\\x=4,6cm </math>
AC = 4,6 cm og BC = 9,2 cm.
Man kan bruke Pytagoras til å sjekke om en gitt trekant er rettvinklet. Man sjekker om kvadratet utspendt av den lengste siden er lik summen av kvadratene utspendt av de to korteste.
Eksempel 4:(spesialtilfelle)
I en trekant er siden 3 meter, 4 meter og 5,5 meter. Er trekanten rettvinklet?
LØSNING:
Dersom trekanten er rettvinklet må den lengste siden være hypotenusen. Det betyr at <math>3^2 + 4^2 = 25</math> må være lik <math>5,5^2</math>. Det er ikke tilfellet, derfor er trekanten ikke rettvinklet.
Firkanter
Kvadrat
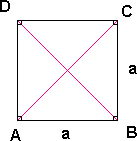
Et kvadrat er en firkant hvor alle sidene er like lange og alle vinklene er 90°. Diagonalene er markert med røde linjer. En diagonal er en rett linje som går fra et hjørne i firkanten til motstående hjørne. Et kvadrat er et spesialtilfelle av et rektangel.
Arealet av kvadratet er:
<math> A = a \cdot a = a^2</math>
Omkretsen av kvadratet er:
<math> O = a + a + a + a = 4a.</math>
Rektangel
Et rektangel er en firkant der sidene er parvis like lange. Vinklene er 90°.
Arealet av rektangelet er: A = ab
Omkretsen er: O = a + a + b + b = 2a + 2b.
Parallellogram
Et parallellogram er en firkant hvor sidene er parvis parallelle.
Areal:
A = ah
Omkrets
O = 2(a+b)
Rombe
En rombe er en firkant der alle sidene er like lange og parvis parallelle. En rombe er et spesialtilfelle av et parallellogram.
Areal:
A = ah
Omkrets:
Da alle sidene er like lange er
a = b = c = d
Da blir
O = 4a
Trapes
I et trapes er to av sidene parallelle. Trapes
Areal:
<math> A= \frac{h \cdot (AB+CD)}{2}</math>
Omkrets:
O = AB + BC + CD + DA