2P 2018 høst LØSNING: Forskjell mellom sideversjoner
| (66 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 4: | Linje 4: | ||
=DEL EN= | =DEL EN= | ||
==Oppgave 1== | ==Oppgave 1== | ||
1, 5 | 1, 5, 1, 3, 3, 1, 4, 2, 4, 0 | ||
I stigende rekkefølge: | I stigende rekkefølge: | ||
0 | 0, 1, 1, 1, 2, 3, 3, 4, 4, 5 | ||
Medianverdi blir gjennomsnittet av tall fem og seks, altså: $\frac{ | Medianverdi blir gjennomsnittet av tall fem og seks, altså: $\frac{2+3}{2} = 2,5$ | ||
Typetall: 1 (den verdi det er mest av) | Typetall: 1 (den verdi det er mest av) | ||
Gjennomsnitt, Summen av verdier, delt på antall verdier. $\frac{0 | Gjennomsnitt, Summen av verdier, delt på antall verdier. $\frac{0+1+1+1+2+3+3+4+4+5}{10}= \frac{24}{10}= 2,4$ | ||
Variasjonsbredde er største verdi minus minste verdi: 5 - 0 = 5. | Variasjonsbredde er største verdi minus minste verdi: 5 - 0 = 5. | ||
==Oppgave 2== | ==Oppgave 2== | ||
Dersom 5% tilsvarer 40 kroner er 1% $\frac{40}{5} = 8$kr. Varen kostet $100 \cdot 8\, kr = 800 \, kr.$ før den ble satt opp. | Dersom 5% tilsvarer 40 kroner er 1% $\frac{40}{5} = 8$kr. Varen kostet $100 \cdot 8\, kr = 800 \, kr.$ før den ble satt opp. | ||
| Linje 44: | Linje 42: | ||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | ===a)=== | ||
| Linje 55: | Linje 52: | ||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | |||
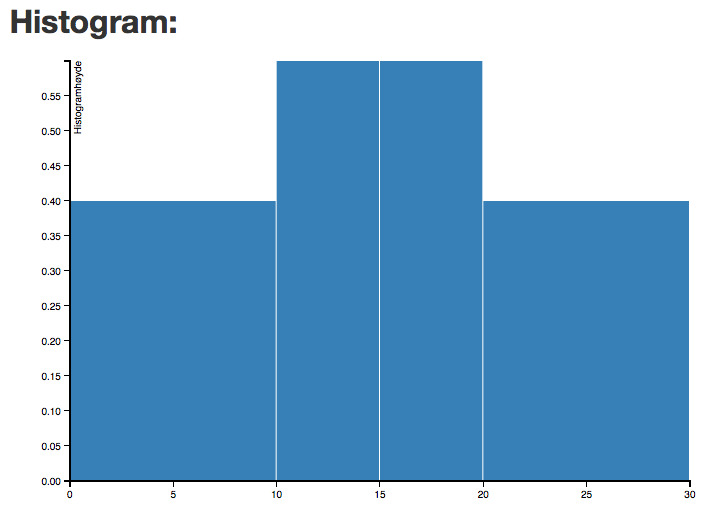
For å finne en tilnærmet verdi for gjennomsnittet i klassedelt materiale må vi anta at verdiene fordeler seg jevnt i hver klasse. | |||
Vi multipliserer klassemidtpunktene med frekvensene, summerer og dividerer på det totale antall, som i dette tilfelle er 14: | |||
$5 \cdot 4 = 20 \\ 12,5 \cdot 3 = 37,5 \\ 17,5 \cdot 3 =52,5 \\ 25 \cdot 4 = 100 \\ 20 + 37,5 + 52,5 + 100 = 210 \\ 210:14 =15$ | |||
===b)=== | |||
[[File:hist6a2ph2018.png]] | |||
$Histogramhøyde = \frac{Frekvens}{Klassebredde}$ | |||
Husk at det er arealet av "søylene" som er viktig. Høyde gange bredde gir frekvensen i hver enkelt klasse. | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
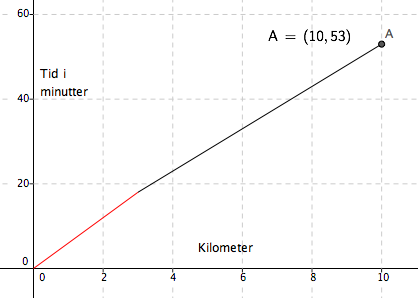
Dersom man løper med 10 km/h bruker man $\frac{1}{10}$ time på 1 km. 1/10 time tilsvar 6 min, siden det er 60 min i en time. | |||
===b)=== | |||
$\frac{1}{12}$ time gir 5 min på en km. | |||
===c)=== | |||
[[File: loepetur2ph2018.png ]] | |||
===d)=== | |||
Hun bruker 53 min på 10 km. altså brukte hun i snitt 5,3 min per km, eller 5 min og 18 sekunder. | |||
==Oppgave 8== | ==Oppgave 8== | ||
===a)=== | |||
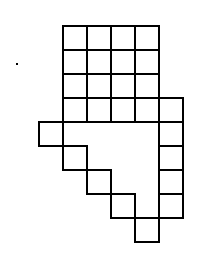
[[File: figurtegning2ph2018.png]] | |||
Figur 4. | |||
===b)=== | |||
Små kvadrater i figur fem: | |||
I denne type oppgave ser jeg alltid etter systemer. Vi ser at alle figurene har et kvadrat der sidekantene tilsvarer figurnummer i antall små kvadrater. Det blir 5 gange 5 som er 25. I tillegg har figuren to rader med små kvadrater som begge har ett mere enn figurtallet, altså 6 +6 = 12. | |||
25 + 12 = 37 små kvadrater i figur 5. | |||
===c)=== | |||
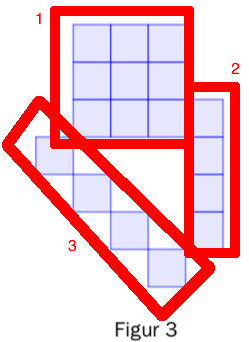
[[File:fork.png ]] | |||
Vi tar utgangspunkt i figur nr. 3. Vi ser at vi kan dele alle figurene inn i tre områder, 1, 2 og 3. Fordi vi har figur nr.3 prøver vi nå å uttrykke antall små kvadrater med 3. Vi ser at: | |||
Område 1: $3 \cdot 3$ | |||
Område 2: 3 + 1 | |||
Område 3: 3 + 1 | |||
For å finne et uttrykk for figur n, erstatter vi alle 3 tall med n og legger sammen: | |||
$(n \cdot n) + (n+1) + (n+1) = n^2 +2n + 2 $ | |||
Vi kan døpe utrykket over til A, antall som funksjon av n og får: | |||
$A(n) = n^2 +2n +2$ | |||
===d)=== | |||
$A(n) = n^2 +2n +2 \\ A(100) = 100^2 + 2 \cdot 100 + 2 \\ A(100)= 10000 + 200 +2 \\ A(100)=10202 $ | |||
=DEL TO= | =DEL TO= | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
[[File:funk2ph18.png ]] | |||
===b)=== | |||
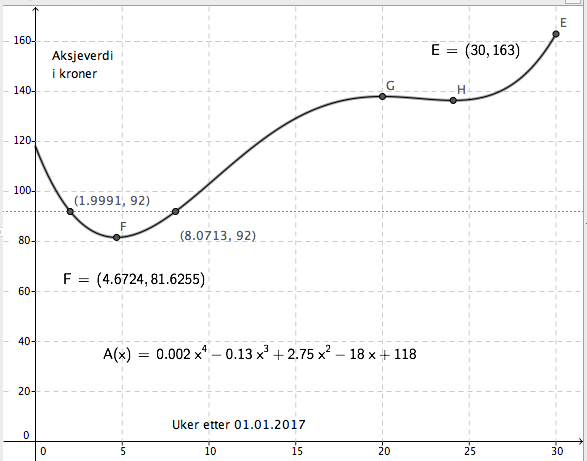
Verdien var lavere enn 92 kroner i ca. 6 uker, fra slutten av uke to til starten av uke ni. | |||
===c)=== | |||
Verdien varierte mellom 81,6 kroner og 163 kroner. Forskjellen var 81, 4 kroner. | |||
===d)=== | |||
163 - 118 = 45 | |||
Aksjen steg med 45 kroner denne perioden. Gjennomsnittlig vekst per uke blir $\frac{45 \, kr }{30 \, uker} = 1,5$ kroner/uke. | |||
===e)=== | |||
[[File:momentan2ph2018.png]] | |||
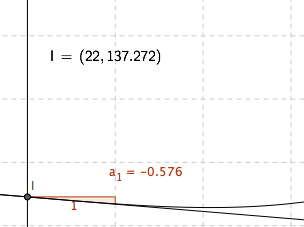
Dag nr. 154 $(22 \cdot 7) $ i 2017 avtar verdien av aksjen med 0,58 kroner. | |||
==Oppgave 2== | ==Oppgave 2== | ||
Her må man lese av diagrammet så godt man kan. Så lenge man viser utregningen og tankegang er det ikke så farlig om man leser av litt feil. Diagrammet er i utgangspunktet ikke svært nøyaktig. | |||
2006 : ca. 155 minutter. | |||
2016: ca. 65 minutter. | |||
(lest av fra blågrå kurve) | |||
Dersom du har litt andre tall vil utregningen bli litt forskjellig, men det gjør ikke noe da dette er sånn cirka hele veien. | |||
Nedgang i seertid var ca. 90 minutter. | |||
I prosent blir nedgangen da $\frac{90}{155} = 0,58$, som er 58%. | |||
==Oppgave 3== | ==Oppgave 3== | ||
[[File:exel2ph2018.png]] [[File:exel2ph20182.png]] | |||
===a)=== | |||
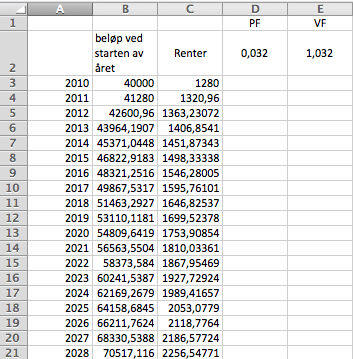
Når rente for 2018 er godskrevet , vil han i starten på 2019 ha 53 110 kroner på konto (se figur over). | |||
===b)=== | |||
I starten på 2023, når rentene for 2022 er godskrevet, passerer han 60 000 kroner. | |||
Det går altså ca. 12 år. | |||
===c)=== | |||
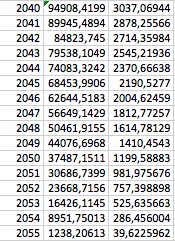
[[File:exe42p2018.png]] | |||
Han kan ta 16 uttak. Det første i 2040 og det siste i 2055. | |||
==Oppgave 4== | ==Oppgave 4== | ||
===a)=== | |||
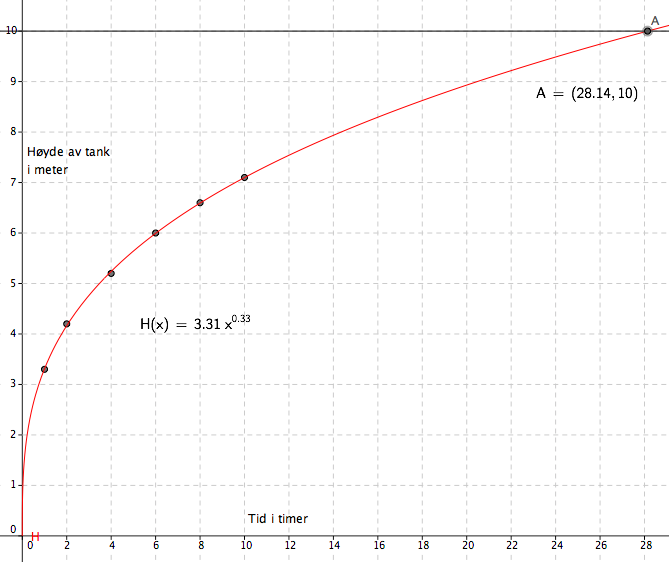
[[File:reg2ph18.png ]] | |||
Modellen passer godt. | |||
===b)=== | |||
Tanken er full når vannhøyden er 10 meter. Det tar 28,14 timer, se figur i a. | |||
Det pumpes inn $18 m^3 = 18 000$ liter per time. Når den er full er det $18000 \frac{liter}{time}\cdot 28,14 timer = 506520 $ liter i tanken. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
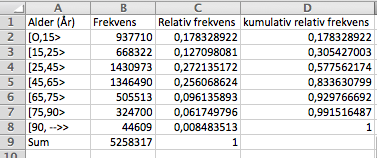
[[File:5a2ph2018.png]] [[File:5a22ph2018.png]] | |||
===b)=== | |||
99,15% er under 90 år. Finner det ved å lese av kumulativ relativ frekvens. | |||
===c)=== | |||
Medianverdien finner man i gruppen 25 - 45 år (30,5% - 57%. fra kumulativ relativ frekvens). | |||
===d)=== | |||
Dersom antallet fordeler seg jevnt i intervallet 25 - 45 er dette ett brukbart estimat på antallet under 30 år. Tallet er summen av alle fra 0 til 25 pluss en fjerdedel i intervallet 25-45 år. | |||
==Oppgave 6== | ==Oppgave 6== | ||
Sjekk skalaene på y aksene, her er det lett å bli lurt!! | |||
===a)=== | |||
[[File: nedbør.png ]] | |||
===b)=== | |||
Se punkt a. (Bruker funksjoner for gjennomsnitt og standardavvik i regnearket). | |||
===c)=== | |||
Det regner mye mere i Brekke (ett av landets mest nedbørrike områder). Derfor er det naturlig at gjennomsnittet her ligger på ca. 250 mm (meningsløst å gi gjennomsnitt og standardavvik med to desimaler som jeg gjorde i a, fordi jeg sikkert har lest litt feil av verdiene i diagrammet). | |||
I brekke er variasjonene store, i Mai måned er nedbørsmengden under 100 mm, mens den i November er nesten 500 mm. At det er store variasjoner i nedbørsmengde fører til et stort standardavvik. | |||
Dersom man ikke sjekker skalaen på y aksen ser det ut som variasjonene i Skjåk er større, men slik er det altså ikke. | |||
==Oppgave 7== | ==Oppgave 7== | ||
'''Situasjon 1''' | |||
Når noe vokser med en gitt PROSENT per tidsrom er det eksponentiell vekst. Grafen vil stige, sakte i begynnelsen, så brattere og brattere. Dette passer med figur A. | |||
'''Situasjon 2''' | |||
Dersom noe minker (avtar , synker) med et gitt ANTALL per tidsrom har vi en lineær sammenheng ( rett linje). Siden det minker er linjen avtagende mot høyre (når tiden øker), altså figur D. | |||
'''Situasjon 3''' | |||
Dersom noe vokser hele tiden vil grafen alltid stige. I denne situasjonen vokser det, men veksten blir mindre med tiden. Det betyr at grafen "flater ut" (ikke helt). Dett passer til figur B. | |||
'''Situasjon 4''' | |||
Når noe avtar med en fast PROSENT per tidsenhet er det eksponentiell vekst (negativ). Grafen synker mye i begynnelsen og mindre etter som tiden går, men den synker hele tiden. Dette passer med figur F. | |||
Siste sideversjon per 4. mai 2019 kl. 10:13
Diskusjon av oppgaven på matteprat
Løsning laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
1, 5, 1, 3, 3, 1, 4, 2, 4, 0
I stigende rekkefølge:
0, 1, 1, 1, 2, 3, 3, 4, 4, 5
Medianverdi blir gjennomsnittet av tall fem og seks, altså: $\frac{2+3}{2} = 2,5$
Typetall: 1 (den verdi det er mest av)
Gjennomsnitt, Summen av verdier, delt på antall verdier. $\frac{0+1+1+1+2+3+3+4+4+5}{10}= \frac{24}{10}= 2,4$
Variasjonsbredde er største verdi minus minste verdi: 5 - 0 = 5.
Oppgave 2
Dersom 5% tilsvarer 40 kroner er 1% $\frac{40}{5} = 8$kr. Varen kostet $100 \cdot 8\, kr = 800 \, kr.$ før den ble satt opp.
Oppgave 3
Kaffe i norge: 1 920 000 liter
Kopp: 1,5 desiliter
1 920 000 l = 19 200 000 dl = $1,92 \cdot 10^7$
Deler totalvolumet på volumet av en kopp:
Det drikkes $\frac{1,92 \cdot 10^7}{1,5} = 1,28 \cdot 10^7$ kopper kaffe i Norge daglig.
Oppgave 4
$3^3 \cdot \frac 19 - 2^3(4-1) = \\ 27 \cdot \frac 19 - 8 \cdot 3 = \\ 3 - 24 = - 21$
Oppgave 5
a)
I kamp nr. 4 scoret hun 21 - 15 = 6 mål.
b)
På 6 kamper scoret hun totalt 30 mål. Det blir i snitt $\frac{30}{6} = 5$ mål per kamp.
Oppgave 6
a)
For å finne en tilnærmet verdi for gjennomsnittet i klassedelt materiale må vi anta at verdiene fordeler seg jevnt i hver klasse.
Vi multipliserer klassemidtpunktene med frekvensene, summerer og dividerer på det totale antall, som i dette tilfelle er 14:
$5 \cdot 4 = 20 \\ 12,5 \cdot 3 = 37,5 \\ 17,5 \cdot 3 =52,5 \\ 25 \cdot 4 = 100 \\ 20 + 37,5 + 52,5 + 100 = 210 \\ 210:14 =15$
b)
$Histogramhøyde = \frac{Frekvens}{Klassebredde}$
Husk at det er arealet av "søylene" som er viktig. Høyde gange bredde gir frekvensen i hver enkelt klasse.
Oppgave 7
a)
Dersom man løper med 10 km/h bruker man $\frac{1}{10}$ time på 1 km. 1/10 time tilsvar 6 min, siden det er 60 min i en time.
b)
$\frac{1}{12}$ time gir 5 min på en km.
c)
d)
Hun bruker 53 min på 10 km. altså brukte hun i snitt 5,3 min per km, eller 5 min og 18 sekunder.
Oppgave 8
a)
Figur 4.
b)
Små kvadrater i figur fem:
I denne type oppgave ser jeg alltid etter systemer. Vi ser at alle figurene har et kvadrat der sidekantene tilsvarer figurnummer i antall små kvadrater. Det blir 5 gange 5 som er 25. I tillegg har figuren to rader med små kvadrater som begge har ett mere enn figurtallet, altså 6 +6 = 12.
25 + 12 = 37 små kvadrater i figur 5.
c)
Vi tar utgangspunkt i figur nr. 3. Vi ser at vi kan dele alle figurene inn i tre områder, 1, 2 og 3. Fordi vi har figur nr.3 prøver vi nå å uttrykke antall små kvadrater med 3. Vi ser at:
Område 1: $3 \cdot 3$
Område 2: 3 + 1
Område 3: 3 + 1
For å finne et uttrykk for figur n, erstatter vi alle 3 tall med n og legger sammen:
$(n \cdot n) + (n+1) + (n+1) = n^2 +2n + 2 $
Vi kan døpe utrykket over til A, antall som funksjon av n og får:
$A(n) = n^2 +2n +2$
d)
$A(n) = n^2 +2n +2 \\ A(100) = 100^2 + 2 \cdot 100 + 2 \\ A(100)= 10000 + 200 +2 \\ A(100)=10202 $
DEL TO
Oppgave 1
a)
b)
Verdien var lavere enn 92 kroner i ca. 6 uker, fra slutten av uke to til starten av uke ni.
c)
Verdien varierte mellom 81,6 kroner og 163 kroner. Forskjellen var 81, 4 kroner.
d)
163 - 118 = 45
Aksjen steg med 45 kroner denne perioden. Gjennomsnittlig vekst per uke blir $\frac{45 \, kr }{30 \, uker} = 1,5$ kroner/uke.
e)
Dag nr. 154 $(22 \cdot 7) $ i 2017 avtar verdien av aksjen med 0,58 kroner.
Oppgave 2
Her må man lese av diagrammet så godt man kan. Så lenge man viser utregningen og tankegang er det ikke så farlig om man leser av litt feil. Diagrammet er i utgangspunktet ikke svært nøyaktig.
2006 : ca. 155 minutter.
2016: ca. 65 minutter.
(lest av fra blågrå kurve) Dersom du har litt andre tall vil utregningen bli litt forskjellig, men det gjør ikke noe da dette er sånn cirka hele veien.
Nedgang i seertid var ca. 90 minutter.
I prosent blir nedgangen da $\frac{90}{155} = 0,58$, som er 58%.
Oppgave 3
a)
Når rente for 2018 er godskrevet , vil han i starten på 2019 ha 53 110 kroner på konto (se figur over).
b)
I starten på 2023, når rentene for 2022 er godskrevet, passerer han 60 000 kroner.
Det går altså ca. 12 år.
c)
Han kan ta 16 uttak. Det første i 2040 og det siste i 2055.
Oppgave 4
a)
Modellen passer godt.
b)
Tanken er full når vannhøyden er 10 meter. Det tar 28,14 timer, se figur i a.
Det pumpes inn $18 m^3 = 18 000$ liter per time. Når den er full er det $18000 \frac{liter}{time}\cdot 28,14 timer = 506520 $ liter i tanken.
Oppgave 5
a)
b)
99,15% er under 90 år. Finner det ved å lese av kumulativ relativ frekvens.
c)
Medianverdien finner man i gruppen 25 - 45 år (30,5% - 57%. fra kumulativ relativ frekvens).
d)
Dersom antallet fordeler seg jevnt i intervallet 25 - 45 er dette ett brukbart estimat på antallet under 30 år. Tallet er summen av alle fra 0 til 25 pluss en fjerdedel i intervallet 25-45 år.
Oppgave 6
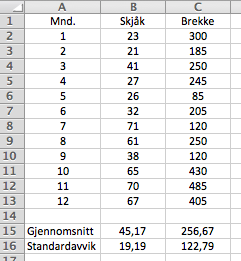
Sjekk skalaene på y aksene, her er det lett å bli lurt!!
a)
b)
Se punkt a. (Bruker funksjoner for gjennomsnitt og standardavvik i regnearket).
c)
Det regner mye mere i Brekke (ett av landets mest nedbørrike områder). Derfor er det naturlig at gjennomsnittet her ligger på ca. 250 mm (meningsløst å gi gjennomsnitt og standardavvik med to desimaler som jeg gjorde i a, fordi jeg sikkert har lest litt feil av verdiene i diagrammet).
I brekke er variasjonene store, i Mai måned er nedbørsmengden under 100 mm, mens den i November er nesten 500 mm. At det er store variasjoner i nedbørsmengde fører til et stort standardavvik.
Dersom man ikke sjekker skalaen på y aksen ser det ut som variasjonene i Skjåk er større, men slik er det altså ikke.
Oppgave 7
Situasjon 1
Når noe vokser med en gitt PROSENT per tidsrom er det eksponentiell vekst. Grafen vil stige, sakte i begynnelsen, så brattere og brattere. Dette passer med figur A.
Situasjon 2
Dersom noe minker (avtar , synker) med et gitt ANTALL per tidsrom har vi en lineær sammenheng ( rett linje). Siden det minker er linjen avtagende mot høyre (når tiden øker), altså figur D.
Situasjon 3
Dersom noe vokser hele tiden vil grafen alltid stige. I denne situasjonen vokser det, men veksten blir mindre med tiden. Det betyr at grafen "flater ut" (ikke helt). Dett passer til figur B.
Situasjon 4
Når noe avtar med en fast PROSENT per tidsenhet er det eksponentiell vekst (negativ). Grafen synker mye i begynnelsen og mindre etter som tiden går, men den synker hele tiden. Dette passer med figur F.