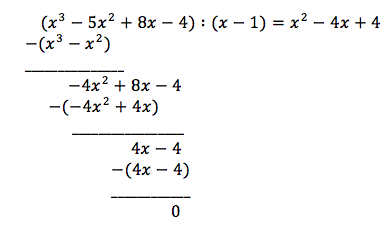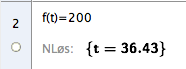S2 2018 høst LØSNING: Forskjell mellom sideversjoner
| (127 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[https://www.matematikk.net/matteprat/viewtopic.php?f=13&t=48351 Diskusjon av oppgaven på matteprat] | [https://www.matematikk.net/matteprat/viewtopic.php?f=13&t=48351 Diskusjon av oppgaven på matteprat] | ||
[https://www.matematikk.net/matteprat/download/file.php?id=2359 Løsning som pdf laget av Svein Arneson pensjonert lektor] [https://www.matematikk.net/matteprat/download/file.php?id=2360 (og som docx)] | |||
=DEL 1= | =DEL 1= | ||
| Linje 16: | Linje 17: | ||
$h(x)=x^3 \cdot ln\, x \\ h'(x)=3x^2 \cdot ln \, x + x^3 \cdot \frac{1}{x} \\ = 3x^2 \cdot ln \, x + x^2$ | $h(x)=x^3 \cdot ln\, x \\ h'(x)=3x^2 \cdot ln \, x + x^3 \cdot \frac{1}{x} \\ = 3x^2 \cdot ln \, x + x^2$ | ||
==Oppgave 2== | |||
Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer. | |||
I slike tilfeller er $\lim_{n\to\infty}S_n=\lim_{n\to\infty}\sum_{i=1}^n a_i=\frac{a_1}{1-k}$ | |||
===a)=== | |||
Vi har rekken $a_n=54 \cdot \frac{1}{3}^{n-1}$. I denne rekka er $k= \frac{1}{3}$. Det vil si at rekken konvergerer. Summen er gitt ved: | |||
$\lim_{n\to\infty}S_n=\frac{54}{1-\frac{1}{3}} = \frac{54}{\frac{2}{3}} = \frac{54 \cdot 3}{2} = 81$ | |||
===b)=== | |||
Vi har rekken $a_n=4 \cdot (-2)^{n-1}$. I denne rekka er $k= -2$. Det vil si at rekken ikke konvergerer. | |||
==Oppgave 3== | ==Oppgave 3== | ||
| Linje 28: | Linje 45: | ||
<td>3 </td> | <td>3 </td> | ||
<td>4 </td> | <td>4 </td> | ||
<td> | <td>$n$ </td> | ||
</tr> | </tr> | ||
| Linje 37: | Linje 54: | ||
<td>20</td> | <td>20</td> | ||
<td>25</td> | <td>25</td> | ||
<td> | <td>$F_n$</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>utregning for å finne formel </td> | <td>utregning for å finne formel </td> | ||
<td>5 | <td>$5\cdot 2$</td> | ||
<td>5 | <td>$5\cdot 3$</td> | ||
<td>5 | <td>$5\cdot 4$</td> | ||
<td>5 | <td>$5\cdot 5$</td> | ||
<td>5 | <td>$5\cdot(n+1) = 5n+5$</td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Inntekten per runde | Inntekten per runde $F_n$ er gitt ved $F_n=5n+5$, der ''n'' er antall runder løpt og $n>0$. Setter $F_n=100$ | ||
$ | $5n+5=100 \\ n+1 = 20 \\ n=19$ | ||
Lise må løpe 19 runder for å tjene 100 kroner på den siste runden. | Lise må løpe 19 runder for å tjene 100 kroner på den siste runden. | ||
| Linje 58: | Linje 75: | ||
===b)=== | ===b)=== | ||
$ S=\sum_{n=1}^{25} 5n+5 \\ = \frac{(5\cdot 1 + 5)+(5\cdot 25 + 5)}{2} \cdot 25 \\ = \frac{10+130}{2} \cdot 25 \\ = 70 \cdot 25 = 1750 $ | |||
Bedriften må gi totalt 1750 kroner dersom Lise løper 25 runder. | |||
==Oppgave 4== | |||
===a)=== | |||
$f(x)=x^3-5x^2+8x-4 \\ f(1)=1^3-5\cdot 1^2 + 8 \cdot 1 - 4=1 -5 + 8 -4 =0$ | |||
Siden $x=1$ er et nullpunkt, så er $(x-1)$ en faktor i $f(x)$. | |||
===b)=== | |||
Vi har allerede funnet en faktor, nemlig (x-1). Utfører polynomdivisjon for å finne resten. | |||
[[File: poldiv.png]] | |||
Faktoriserer nå resten ved å kjenne igjen andre kvadratsetning: | |||
$x^2-4x+4=x^2-2\cdot 2 + 2^2=(x-2)(x-2)$ | |||
Vi har da: | |||
$f(x)=x^3-5x^2+8x-4=(x-1)(x-2)(x-2)$ | |||
===c)=== | |||
Kjenner igjen konjugatetningen i nevneren. | |||
$\frac{x^3-5x^2+8x-d}{x^2-4}=\frac{x^3-5x^2+8x-d}{(x+2)(x-2)}$ | |||
Brøken kan forkortes for $d=-4$, slik vi hadde for $f(x)$, hvor $(x-2)$ var en faktor. | |||
Brøken kan også forkortes derom $(x+2)$ er en faktor, og da er $x=-2$. Finner ut hvilken verdi $d$ må ha for at $(x+2)$ skal være en faktor: | |||
$(-2)^3-5\cdot (-2)^2+8\cdot (-2)+d=0 \\ -8-20-16+d=0 \\ d=44$ | |||
Brøken kan forkortes for $d=-4$ eller $d=44$. | |||
==Oppgave 5== | |||
===a)=== | |||
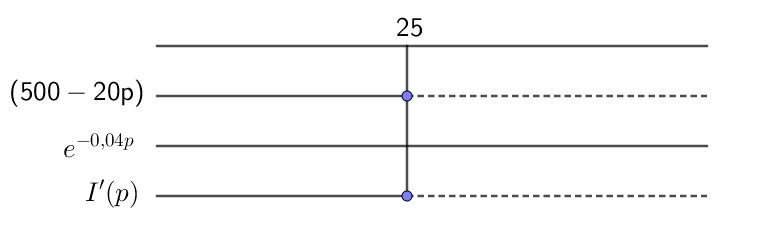
$I(p)=p\cdot q(p)=p\cdot 500\cdot e^{-0,04p}$ | |||
Finner størst inntekt ved derivasjon: | |||
$I'(p)=500 \cdot e^{-0,04p} + 500p \cdot (-0,04) \cdot e^{-0,04p} \\ = 500 \cdot e^{-0,04p} -20p \cdot e^{-0,04p} \\ =(500-20p)\cdot e^{-0,04p}$ | |||
$I'(p)=0 \\ (500-20p)\cdot e^{-0,04p}=0 \quad \Rightarrow \quad (500-20p)=0 \\ p=\frac{500}{20}=25 $ | |||
[[File: S2_H18_Del1_5.png]] | |||
Vi har et toppunkt i p=25. Det vil si at en pris på 25 kr gir maksimal inntekt. | |||
===b)=== | |||
$q=500\cdot e^{-0,04p} \\ \frac{q}{500}=e^{-\frac{1}{25} p} \\ ln \lgroup \frac{q}{500} \rgroup=-\frac{1}{25} p \\ -25\, ln \lgroup \frac{q}{500}\rgroup=p \\ p(q)=-25\, ln \lgroup \frac{q}{500}\rgroup$ | |||
===c)=== | |||
$p(q)=-25\, ln \lgroup \frac{q}{500}\rgroup$ | |||
$p(q)=g(u(q))= -25 \, ln(u) \quad , u=\frac{q}{500}$ | |||
$p'(q)=g'(u)\cdot u'(q)$ | |||
$p'(q)=-25 \cdot \frac{1}{u} \cdot u'$ | |||
$p'(q)=-25 \cdot \frac{1}{\frac{q}{500}} \cdot \frac{1}{500} =-\frac{25}{q} \\ p'(25)=-\frac{25}{25}=-1$ | |||
Svaret forteller oss at ved en etterspørsel på 25 enheter, vil prisen synke med 1 krone per enhet. | |||
==Oppgave 6== | |||
===a)=== | |||
Vi har $f(x)=ax^3+bx^2+cx+d$, der a,b,c og d er konstanter. | |||
* x=1 er et nullpunkt, det vil si at $f(1)=0$ . | |||
$\quad f(1)=a\cdot 1^3 + b \cdot 1^2 + c\cdot 1 + d = a+b+c+d=0$ | |||
* x=-2 er et nullpunkt, det vil si at $f(-2)=0$. | |||
$\quad f(-2)=a\cdot(-2)^3+b\cdot(-2)^2+c\cdot(-2)+d=-8a+4b-2c+d=0$ | |||
* x=1 er ekstremalpunktet, det vil si at $f'(1)=0$. | |||
$\quad f'(x)=3ax^2+2bx+c\\ \quad f'(1)=3a\cdot 1^2 + 2b\cdot 1+c=3a+2b+c=0$ | |||
* At grafen til ''f'' skjærer y-aksen i y=2 forteller oss at konstantleddet d=2. | |||
===b)=== | |||
$I \quad \quad a+b+c+d=0 \\ II \quad -8a+4b-2c+2=0 \\ III \quad 3a+2b+c=0 \\ IV \quad d=2 $ | |||
Bruker at d=2 og trekker likning I fra likning III. | |||
$3a-a+2b-b+c-c-2=0 \\ 2a+b=2 \\ b=-2a+2$ | |||
Ganger likning I med 2, og legger dette sammen med likning III. | |||
$2a-8a+2b+4b+2c-2c+4+2=0 \\ -6a+6b+6=0 \quad :6 \\ -a+b+1=0$ | |||
Setter inn $b=-2a+2$ | |||
$-a-2a+2+1=0 \\ 3a=3 \\ a=1$ | |||
$b=-2\cdot 1 + 2 = 0$ | |||
Bruker at d=2, og bruker likning $I$ til å finne et uttrykk for c: | |||
$a+b+c+d=0 \quad \Rightarrow \quad c=-a-b-2 = -1-0-2=-3$ | |||
Vi har $a=1,\,b=0,\,c=-3$ | |||
Bestemmer uttrykket for f(x): | |||
$f(x)=ax^3+bx^2+cx+6 \\ f(x)=x^3-3x+2$ | |||
==Oppgave 7== | |||
===a)=== | |||
La X være gevinsten spilleren får når terningen kastes én gang. | |||
{| | |||
!x | |||
!0 | |||
!20 | |||
!60 | |||
!200 | |||
|- | |||
!$P(X=x)$ | |||
|$\frac{1}{3}$ | |||
|$\frac{1}{3}$ | |||
|$\frac{1}{6}$ | |||
|$\frac{1}{6}$ | |||
|} | |||
===b)=== | |||
Finner forventningsverdien $E(x)=\mu$ | |||
$\mu=0\cdot P(X=0) + 20\cdot P(X=20) + 60\cdot P(X=60)+ 200\cdot P(X=200) \\ = 0 + 20\cdot \frac{1}{3} + 60\cdot \frac{1}{6} + 200\cdot \frac{1}{6} \\ = \frac{20}{3}+\frac{30}{3} +\frac{100}{3} = \frac{150}{3} = 50 $ | |||
Forventningsverdien er 50 kroner. | |||
Finner variansen $Var(X)$ | |||
$Var(X)=(0-\mu)^2\cdot P(X=0) + (20-\mu)^2\cdot P(X=20) + (60-\mu)^2\cdot P(X=60)+ (200-\mu)^2\cdot P(X=200) \\ = (0-50)^2 \cdot \frac{1}{3} + (20-50)^2 \cdot \frac{1}{3} +(60-50)^2 \cdot \frac{1}{6} + (200-50)^2 \cdot \frac{1}{6} \\ = \frac{2500}{3}+\frac{900}{3} +\frac{100}{6} + \frac{22500}{6}\\ = \frac{2500}{3}+\frac{900}{3} +\frac{50}{3} + \frac{11250}{3}\\ =\frac{14700}{3}=4900$ | |||
Finner $SD(X)=\sqrt{Var(X)}$ | |||
$SD(X)=\sqrt{4900} = 70$ | |||
===c)=== | |||
Prisen per spill må være 60 kroner dersom jeg som arrangør i det lange løp skal få et overskudd på 10 kroner per spill. | |||
===d)=== | |||
S er ifølge sentralgrensesetningen tilnærmet normalfordelt, fordi vi gjentar spillet 100 ganger. Sentralgrensesetningen sier følgende: | |||
La ''X'' være en stokastisk variabel med forventningsverdi $\mu$ og standardavvik $\sigma$. | |||
La $\Sigma_n X$ være summen av ''n'' uavhengige forsøk med ''X''. | |||
For store verdier av ''n'' er $\Sigma_n X$ tilnærmet normalfordelt. | |||
===e)=== | |||
$E(X)=-10$ fordi forventningsverdien for spilleren er -10 kroner per spill. | |||
$E(S)=\mu=n\cdot \mu = 100\cdot (-10) = -1000$ | |||
Det betyr at forventningsverdien for 100 spill er -1000 kroner. | |||
Standardavviket for gevinst er det samme som før, SD(X)=70. | |||
$SD(S)=\sigma =\sqrt{n} \cdot \sigma = \sqrt{100} \cdot 70 = 10 \cdot 70 = 700$ | |||
Det betyr at standardavviket for 100 spill er 700 kroner. | |||
===f)=== | |||
$z=\frac{0-\mu}{\sigma} = \frac{0-(-1000)}{700} = \frac{10}{7}=1,43$ | |||
$P(S>0)=P((Z>0) =1-P(Z<1,43)=1-0,9236=0,0764$ | |||
Sannsynligheten for at spilleren går i overskudd med de 100 spillene er 0,0764 = 7,64%. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
Bruker CAS i Geogebra til å finne et uttrykk for overskuddet, O(x) | |||
[[File: S2_H18_del2_1a1.png]] | |||
Bruker Geogebra til å tegne grafen til $O_2(x)$. | |||
[[File: S2_H18_del2_1a3.png]] | |||
===b)=== | |||
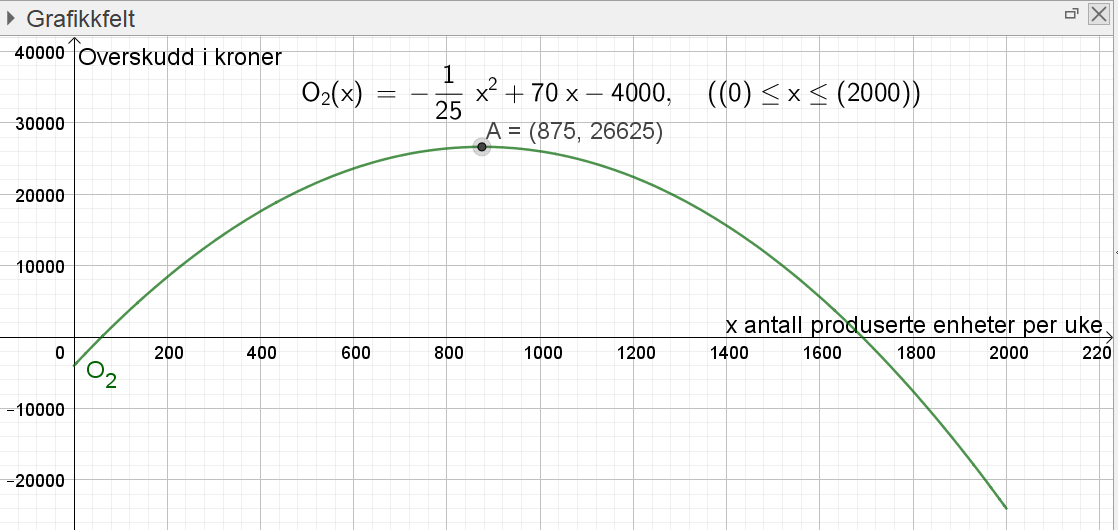
Bruker kommandoen $Ekstremalpunkt[O_2]$ til å bestemme den produksjonsmengden som gir størst overskudd. | |||
[[File: S2_H18_del2_1b.png]] | |||
Den produksjonsmengden som gir størst overskudd er 875 enheter i uka, se punkt A. | |||
===c)=== | |||
[[File: S2_H18_del2_1c.png]] | |||
Jeg finner ekstremalpunkt for a(x), kostnad per enhet, i x=400 og x=-400. Forkaster x=-400, siden vi bare ser på $x\in \langle 0 , 2000 \rangle$. Sjekker at det er et bunnpunkt (og ikke et toppunkt) i x=400 ved å se at funksjonen synker i x=350 og øker i x=450. | |||
Den produksjonsmengden som gir lavest kostnad per enhet, er 400 enheter i uka. | |||
==Oppgave 2== | |||
===a)=== | |||
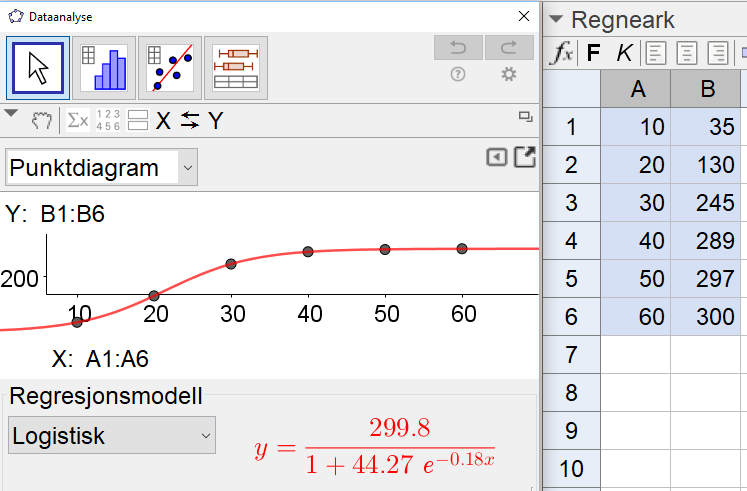
Bruker Geogebra til å utføre en regresjonsanalyse. Velger logistisk regresjonsmodell. | |||
[[File: S2_H18_del2_2a.png]] | |||
En funksjon som beskriver sammenhengen mellom tiden ''t'' og antall skadedyr i dette huset, er | |||
$g(t)=\frac{299,8}{1+44,27e^{-0,18t}}$ | |||
===b)=== | |||
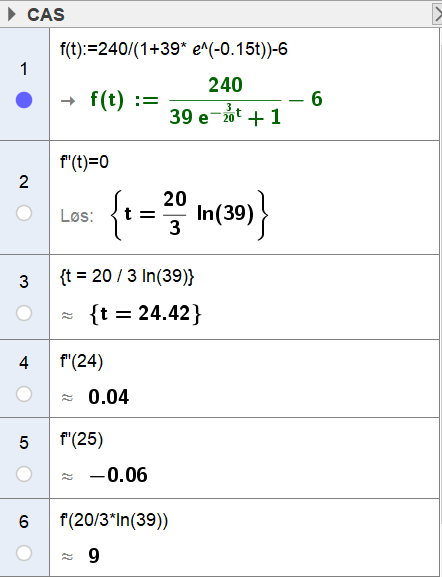
Bruker CAS i Geogebra til å løse oppgaven. | |||
[[File: S2_H18_del2_2b2.png]] | |||
Antall skadedyr økte raskest i $t=\frac{20}{3} \cdot ln(39) \approx 24$ dager etter at huset ble invadert. Dette er vendepunktet til $f(t)$. Sjekker i linje 4 og 5 at $f ' '(t) $ skifter fortegn slik at $ f(t) $ har et vendepunkt. Da var vekstfarten på 9 skadedyr per dag. | |||
===c)=== | |||
Bruker CAS i Geogebra til å løse oppgaven. | |||
[[File: S2_H18_del2_2c2.png]] | |||
Det hadde vært skadedyr i ca. 36 dager da huset ble kontrollert. Denne oppgaven kan også løses grafisk. | |||
==Oppgave 3== | |||
===a)=== | |||
La S være summen av ''n'' poengskårer ''X''. Da er forventningsverdien av summen: | |||
$E(S) = n\cdot E(X)$ | |||
Følgelig er | |||
$E(\overline{X})=E(\frac{S}{n})=\frac{n\cdot E(X)}{n}=E(X)=50$ | |||
Variansen av summen er: | |||
$Var(S) = n\cdot Var(X)$ | |||
Standardavviket av summen er da: | |||
$SD(S)=\sqrt{Var(S)}=\sqrt{n\cdot Var(X)}=\sqrt{n}\cdot SD(X)$ | |||
Følgelig er | |||
$SD(\overline{X})=SD\lgroup \frac{S}{n} \rgroup= \frac{\sqrt{n}\cdot SD(X)}{n}=\frac {\sqrt{100}\cdot 8}{100}=0,8$ | |||
===b)=== | |||
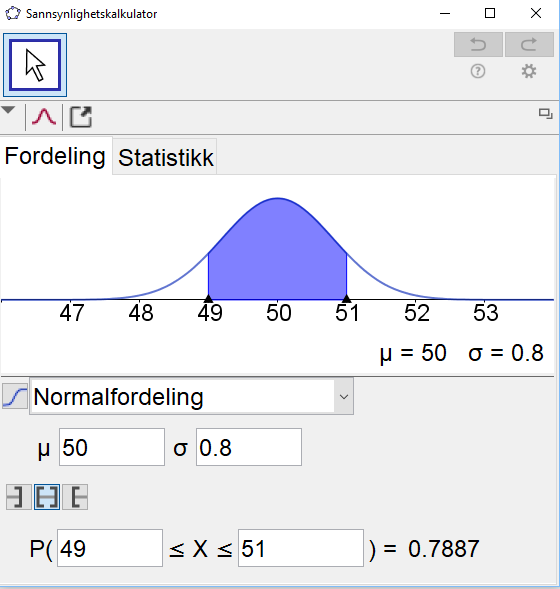
Oppgaven kan løses i sannsynlighetskalkulatoren på Geogebra. Vi har $\mu=E (\overline{X})=50$ og $\sigma= SD(\overline{X})=0,8$. | |||
[[File: S2_H18_del 2_3b.png]] | |||
Sannsynligheten for at gjennomsnittsskåren til de 100 elevene blir mellom 49 og 51 poeng er 78,87%. | |||
===c)=== | |||
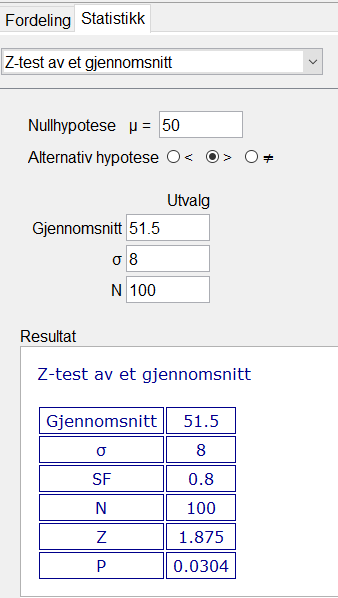
Nullhypotesen er at elevene dette året var like flinke som normalt, med gjennomsnittsskår på 50 poeng på matematikktesten, og standardavvik på 8 poeng. | |||
$H_0: \mu=50$ | |||
Alternativ hypotese er at elevene på denne skolen er flinkere enn normalt. | |||
$H_A: \mu>50$. | |||
Bruker sannsynlighetskalkulatoren i Geogebra for å gjennomføre en Z-test av et gjennomsnitt. | |||
[[File: S2_H18_del2_3c.png]] | |||
P-verdien er 3,04%, som er lavere enn signifikansnivået på 5%. Vi kan dermed forkaste nullhypotesen, og si at elevene dette året var flinkere enn normalt. | |||
==Oppgave 4== | |||
===a)=== | |||
Dette kan uttrykkes som summen av en geometrisk rekke hvor mengden virkestoff fra én tablett etter n døgn er | |||
$a_n=a_1 \cdot k^{n-1}=2,4\cdot 0,75^{n-1}$ | |||
Summen av virkestoff etter 7 døgn kan regnes ut på denne måten: | |||
$S_7=a_1\frac{k^7-1}{k-1}=2,4\cdot \lgroup \frac{0,75^{7}-1}{0,75-1} \rgroup = 8,32$ | |||
Etter 7 døgn har Mads 8,32 mg virkestoff i kroppen. | |||
===b)=== | |||
Denne rekken vil etterhvert konvergere mot følgende verdi: | |||
$\lim_{n\to\infty}S_n=\frac{a_1}{1-k}=\frac{2,4}{1-0,75}=9,6$ | |||
Mads vil maksimalt ha 9,6 mg virkestoff i kroppen i det lange løp hvis han fortsetter medisineringen. | |||
===c)=== | |||
Bruker CAS i Geogebra til å løse oppgaven. Beregner først hva vekstfaktoren må være dersom rekken skal konvergere mot 5,5 mg (se rad 1). Beregner deretter hvor mange døgn det tar før én tablett har blitt brutt ned til $\frac{31}{55}$ av opprinnelig dose på 2,4 mg (se rad 2). | |||
[[File: S2_H18_del2_4d.png]] | |||
Det må minst gå $1,99 \approx 2$ døgn, det vil si omtrent 48 timer mellom hver gang Mads tar en tablett. | |||
Siste sideversjon per 23. mar. 2019 kl. 19:26
Diskusjon av oppgaven på matteprat
Løsning som pdf laget av Svein Arneson pensjonert lektor (og som docx)
DEL 1
Oppgave 1
a)
$f(x)=e^{2x} \\ f'(x)=2e^{2x}$
b)
$g(x)=\frac{x^4-1}{x^2} \\ g'(x)=\frac{4x^3 \cdot x^2 - (x^4-1) \cdot 2x }{(x^2)^2} \\ =\frac{4x^5-2x^5+2x}{x^4} \\ =\frac{2x^5+2x}{x^4} \\ = \frac{2x^4+2}{x^3}$
c)
$h(x)=x^3 \cdot ln\, x \\ h'(x)=3x^2 \cdot ln \, x + x^3 \cdot \frac{1}{x} \\ = 3x^2 \cdot ln \, x + x^2$
Oppgave 2
Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1k^{n-1}$ sier vi at den konvergerer.
I slike tilfeller er $\lim_{n\to\infty}S_n=\lim_{n\to\infty}\sum_{i=1}^n a_i=\frac{a_1}{1-k}$
a)
Vi har rekken $a_n=54 \cdot \frac{1}{3}^{n-1}$. I denne rekka er $k= \frac{1}{3}$. Det vil si at rekken konvergerer. Summen er gitt ved:
$\lim_{n\to\infty}S_n=\frac{54}{1-\frac{1}{3}} = \frac{54}{\frac{2}{3}} = \frac{54 \cdot 3}{2} = 81$
b)
Vi har rekken $a_n=4 \cdot (-2)^{n-1}$. I denne rekka er $k= -2$. Det vil si at rekken ikke konvergerer.
Oppgave 3
a)
| x runder løpt | 1 | 2 | 3 | 4 | $n$ |
| f(x) kroner tjent per runde | 10 | 15 | 20 | 25 | $F_n$ |
| utregning for å finne formel | $5\cdot 2$ | $5\cdot 3$ | $5\cdot 4$ | $5\cdot 5$ | $5\cdot(n+1) = 5n+5$ |
Inntekten per runde $F_n$ er gitt ved $F_n=5n+5$, der n er antall runder løpt og $n>0$. Setter $F_n=100$
$5n+5=100 \\ n+1 = 20 \\ n=19$
Lise må løpe 19 runder for å tjene 100 kroner på den siste runden.
b)
$ S=\sum_{n=1}^{25} 5n+5 \\ = \frac{(5\cdot 1 + 5)+(5\cdot 25 + 5)}{2} \cdot 25 \\ = \frac{10+130}{2} \cdot 25 \\ = 70 \cdot 25 = 1750 $
Bedriften må gi totalt 1750 kroner dersom Lise løper 25 runder.
Oppgave 4
a)
$f(x)=x^3-5x^2+8x-4 \\ f(1)=1^3-5\cdot 1^2 + 8 \cdot 1 - 4=1 -5 + 8 -4 =0$
Siden $x=1$ er et nullpunkt, så er $(x-1)$ en faktor i $f(x)$.
b)
Vi har allerede funnet en faktor, nemlig (x-1). Utfører polynomdivisjon for å finne resten.
Faktoriserer nå resten ved å kjenne igjen andre kvadratsetning:
$x^2-4x+4=x^2-2\cdot 2 + 2^2=(x-2)(x-2)$
Vi har da:
$f(x)=x^3-5x^2+8x-4=(x-1)(x-2)(x-2)$
c)
Kjenner igjen konjugatetningen i nevneren.
$\frac{x^3-5x^2+8x-d}{x^2-4}=\frac{x^3-5x^2+8x-d}{(x+2)(x-2)}$
Brøken kan forkortes for $d=-4$, slik vi hadde for $f(x)$, hvor $(x-2)$ var en faktor.
Brøken kan også forkortes derom $(x+2)$ er en faktor, og da er $x=-2$. Finner ut hvilken verdi $d$ må ha for at $(x+2)$ skal være en faktor:
$(-2)^3-5\cdot (-2)^2+8\cdot (-2)+d=0 \\ -8-20-16+d=0 \\ d=44$
Brøken kan forkortes for $d=-4$ eller $d=44$.
Oppgave 5
a)
$I(p)=p\cdot q(p)=p\cdot 500\cdot e^{-0,04p}$
Finner størst inntekt ved derivasjon:
$I'(p)=500 \cdot e^{-0,04p} + 500p \cdot (-0,04) \cdot e^{-0,04p} \\ = 500 \cdot e^{-0,04p} -20p \cdot e^{-0,04p} \\ =(500-20p)\cdot e^{-0,04p}$
$I'(p)=0 \\ (500-20p)\cdot e^{-0,04p}=0 \quad \Rightarrow \quad (500-20p)=0 \\ p=\frac{500}{20}=25 $
Vi har et toppunkt i p=25. Det vil si at en pris på 25 kr gir maksimal inntekt.
b)
$q=500\cdot e^{-0,04p} \\ \frac{q}{500}=e^{-\frac{1}{25} p} \\ ln \lgroup \frac{q}{500} \rgroup=-\frac{1}{25} p \\ -25\, ln \lgroup \frac{q}{500}\rgroup=p \\ p(q)=-25\, ln \lgroup \frac{q}{500}\rgroup$
c)
$p(q)=-25\, ln \lgroup \frac{q}{500}\rgroup$
$p(q)=g(u(q))= -25 \, ln(u) \quad , u=\frac{q}{500}$
$p'(q)=g'(u)\cdot u'(q)$
$p'(q)=-25 \cdot \frac{1}{u} \cdot u'$
$p'(q)=-25 \cdot \frac{1}{\frac{q}{500}} \cdot \frac{1}{500} =-\frac{25}{q} \\ p'(25)=-\frac{25}{25}=-1$
Svaret forteller oss at ved en etterspørsel på 25 enheter, vil prisen synke med 1 krone per enhet.
Oppgave 6
a)
Vi har $f(x)=ax^3+bx^2+cx+d$, der a,b,c og d er konstanter.
- x=1 er et nullpunkt, det vil si at $f(1)=0$ .
$\quad f(1)=a\cdot 1^3 + b \cdot 1^2 + c\cdot 1 + d = a+b+c+d=0$
- x=-2 er et nullpunkt, det vil si at $f(-2)=0$.
$\quad f(-2)=a\cdot(-2)^3+b\cdot(-2)^2+c\cdot(-2)+d=-8a+4b-2c+d=0$
- x=1 er ekstremalpunktet, det vil si at $f'(1)=0$.
$\quad f'(x)=3ax^2+2bx+c\\ \quad f'(1)=3a\cdot 1^2 + 2b\cdot 1+c=3a+2b+c=0$
- At grafen til f skjærer y-aksen i y=2 forteller oss at konstantleddet d=2.
b)
$I \quad \quad a+b+c+d=0 \\ II \quad -8a+4b-2c+2=0 \\ III \quad 3a+2b+c=0 \\ IV \quad d=2 $
Bruker at d=2 og trekker likning I fra likning III.
$3a-a+2b-b+c-c-2=0 \\ 2a+b=2 \\ b=-2a+2$
Ganger likning I med 2, og legger dette sammen med likning III.
$2a-8a+2b+4b+2c-2c+4+2=0 \\ -6a+6b+6=0 \quad :6 \\ -a+b+1=0$
Setter inn $b=-2a+2$
$-a-2a+2+1=0 \\ 3a=3 \\ a=1$
$b=-2\cdot 1 + 2 = 0$
Bruker at d=2, og bruker likning $I$ til å finne et uttrykk for c:
$a+b+c+d=0 \quad \Rightarrow \quad c=-a-b-2 = -1-0-2=-3$
Vi har $a=1,\,b=0,\,c=-3$
Bestemmer uttrykket for f(x):
$f(x)=ax^3+bx^2+cx+6 \\ f(x)=x^3-3x+2$
Oppgave 7
a)
La X være gevinsten spilleren får når terningen kastes én gang.
| x | 0 | 20 | 60 | 200 |
|---|---|---|---|---|
| $P(X=x)$ | $\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{6}$ |
b)
Finner forventningsverdien $E(x)=\mu$
$\mu=0\cdot P(X=0) + 20\cdot P(X=20) + 60\cdot P(X=60)+ 200\cdot P(X=200) \\ = 0 + 20\cdot \frac{1}{3} + 60\cdot \frac{1}{6} + 200\cdot \frac{1}{6} \\ = \frac{20}{3}+\frac{30}{3} +\frac{100}{3} = \frac{150}{3} = 50 $
Forventningsverdien er 50 kroner.
Finner variansen $Var(X)$
$Var(X)=(0-\mu)^2\cdot P(X=0) + (20-\mu)^2\cdot P(X=20) + (60-\mu)^2\cdot P(X=60)+ (200-\mu)^2\cdot P(X=200) \\ = (0-50)^2 \cdot \frac{1}{3} + (20-50)^2 \cdot \frac{1}{3} +(60-50)^2 \cdot \frac{1}{6} + (200-50)^2 \cdot \frac{1}{6} \\ = \frac{2500}{3}+\frac{900}{3} +\frac{100}{6} + \frac{22500}{6}\\ = \frac{2500}{3}+\frac{900}{3} +\frac{50}{3} + \frac{11250}{3}\\ =\frac{14700}{3}=4900$
Finner $SD(X)=\sqrt{Var(X)}$
$SD(X)=\sqrt{4900} = 70$
c)
Prisen per spill må være 60 kroner dersom jeg som arrangør i det lange løp skal få et overskudd på 10 kroner per spill.
d)
S er ifølge sentralgrensesetningen tilnærmet normalfordelt, fordi vi gjentar spillet 100 ganger. Sentralgrensesetningen sier følgende:
La X være en stokastisk variabel med forventningsverdi $\mu$ og standardavvik $\sigma$.
La $\Sigma_n X$ være summen av n uavhengige forsøk med X.
For store verdier av n er $\Sigma_n X$ tilnærmet normalfordelt.
e)
$E(X)=-10$ fordi forventningsverdien for spilleren er -10 kroner per spill.
$E(S)=\mu=n\cdot \mu = 100\cdot (-10) = -1000$
Det betyr at forventningsverdien for 100 spill er -1000 kroner.
Standardavviket for gevinst er det samme som før, SD(X)=70.
$SD(S)=\sigma =\sqrt{n} \cdot \sigma = \sqrt{100} \cdot 70 = 10 \cdot 70 = 700$
Det betyr at standardavviket for 100 spill er 700 kroner.
f)
$z=\frac{0-\mu}{\sigma} = \frac{0-(-1000)}{700} = \frac{10}{7}=1,43$
$P(S>0)=P((Z>0) =1-P(Z<1,43)=1-0,9236=0,0764$
Sannsynligheten for at spilleren går i overskudd med de 100 spillene er 0,0764 = 7,64%.
DEL 2
Oppgave 1
a)
Bruker CAS i Geogebra til å finne et uttrykk for overskuddet, O(x)
Bruker Geogebra til å tegne grafen til $O_2(x)$.
b)
Bruker kommandoen $Ekstremalpunkt[O_2]$ til å bestemme den produksjonsmengden som gir størst overskudd.
Den produksjonsmengden som gir størst overskudd er 875 enheter i uka, se punkt A.
c)
Jeg finner ekstremalpunkt for a(x), kostnad per enhet, i x=400 og x=-400. Forkaster x=-400, siden vi bare ser på $x\in \langle 0 , 2000 \rangle$. Sjekker at det er et bunnpunkt (og ikke et toppunkt) i x=400 ved å se at funksjonen synker i x=350 og øker i x=450.
Den produksjonsmengden som gir lavest kostnad per enhet, er 400 enheter i uka.
Oppgave 2
a)
Bruker Geogebra til å utføre en regresjonsanalyse. Velger logistisk regresjonsmodell.
En funksjon som beskriver sammenhengen mellom tiden t og antall skadedyr i dette huset, er
$g(t)=\frac{299,8}{1+44,27e^{-0,18t}}$
b)
Bruker CAS i Geogebra til å løse oppgaven.
Antall skadedyr økte raskest i $t=\frac{20}{3} \cdot ln(39) \approx 24$ dager etter at huset ble invadert. Dette er vendepunktet til $f(t)$. Sjekker i linje 4 og 5 at $f ' '(t) $ skifter fortegn slik at $ f(t) $ har et vendepunkt. Da var vekstfarten på 9 skadedyr per dag.
c)
Bruker CAS i Geogebra til å løse oppgaven.
Det hadde vært skadedyr i ca. 36 dager da huset ble kontrollert. Denne oppgaven kan også løses grafisk.
Oppgave 3
a)
La S være summen av n poengskårer X. Da er forventningsverdien av summen:
$E(S) = n\cdot E(X)$
Følgelig er
$E(\overline{X})=E(\frac{S}{n})=\frac{n\cdot E(X)}{n}=E(X)=50$
Variansen av summen er:
$Var(S) = n\cdot Var(X)$
Standardavviket av summen er da:
$SD(S)=\sqrt{Var(S)}=\sqrt{n\cdot Var(X)}=\sqrt{n}\cdot SD(X)$
Følgelig er
$SD(\overline{X})=SD\lgroup \frac{S}{n} \rgroup= \frac{\sqrt{n}\cdot SD(X)}{n}=\frac {\sqrt{100}\cdot 8}{100}=0,8$
b)
Oppgaven kan løses i sannsynlighetskalkulatoren på Geogebra. Vi har $\mu=E (\overline{X})=50$ og $\sigma= SD(\overline{X})=0,8$.
Sannsynligheten for at gjennomsnittsskåren til de 100 elevene blir mellom 49 og 51 poeng er 78,87%.
c)
Nullhypotesen er at elevene dette året var like flinke som normalt, med gjennomsnittsskår på 50 poeng på matematikktesten, og standardavvik på 8 poeng.
$H_0: \mu=50$
Alternativ hypotese er at elevene på denne skolen er flinkere enn normalt.
$H_A: \mu>50$.
Bruker sannsynlighetskalkulatoren i Geogebra for å gjennomføre en Z-test av et gjennomsnitt.
P-verdien er 3,04%, som er lavere enn signifikansnivået på 5%. Vi kan dermed forkaste nullhypotesen, og si at elevene dette året var flinkere enn normalt.
Oppgave 4
a)
Dette kan uttrykkes som summen av en geometrisk rekke hvor mengden virkestoff fra én tablett etter n døgn er
$a_n=a_1 \cdot k^{n-1}=2,4\cdot 0,75^{n-1}$
Summen av virkestoff etter 7 døgn kan regnes ut på denne måten:
$S_7=a_1\frac{k^7-1}{k-1}=2,4\cdot \lgroup \frac{0,75^{7}-1}{0,75-1} \rgroup = 8,32$
Etter 7 døgn har Mads 8,32 mg virkestoff i kroppen.
b)
Denne rekken vil etterhvert konvergere mot følgende verdi:
$\lim_{n\to\infty}S_n=\frac{a_1}{1-k}=\frac{2,4}{1-0,75}=9,6$
Mads vil maksimalt ha 9,6 mg virkestoff i kroppen i det lange løp hvis han fortsetter medisineringen.
c)
Bruker CAS i Geogebra til å løse oppgaven. Beregner først hva vekstfaktoren må være dersom rekken skal konvergere mot 5,5 mg (se rad 1). Beregner deretter hvor mange døgn det tar før én tablett har blitt brutt ned til $\frac{31}{55}$ av opprinnelig dose på 2,4 mg (se rad 2).
Det må minst gå $1,99 \approx 2$ døgn, det vil si omtrent 48 timer mellom hver gang Mads tar en tablett.