2P 2017 vår LØSNING: Forskjell mellom sideversjoner
| (35 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 35: | Linje 35: | ||
For å finne antall molekyler i 1,5 dL, deler vi på 100 og ganger med 1,5: | For å finne antall molekyler i 1,5 dL, deler vi på 100 og ganger med 1,5: | ||
$3,0 \cdot 10^{25} \cdot \frac{1,5}{100} = 3,0 \cdot 1,5 \cdot \frac{10^{25}}{100}= 4,5 \cdot 10^{23}$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
| Linje 69: | Linje 69: | ||
===b)=== | ===b)=== | ||
For å finne gjennomsnitt eller median må vi ANTA at verdiene er jevnt fordelt i hver klasse. Viktig å huske det når man bruker resultatene. De vil bare være sånn halveis gode, men det beste vi har og trolig gode nok. | |||
Gjennomsnitt = | Gjennomsnitt = $ \frac{15 \cdot 100 + 40 \cdot 100 + 60 \cdot600 + 85 \cdot 200}{1000}= 58,50$ | ||
Gjennomsnittet er 58,5. | |||
===c)=== | ===c)=== | ||
Dersom det er medianeleven er 3525 : 2 = 1762,5, hvilket betyr at median er 1763. Vi ser at de ligger i klassen 50 - 70 poeng. | |||
De to klassene før har 563 + 700 = 1263 elementer. Vi skal altså 500 elementer "inn" i 50- 70 klassen. Forutsatt jevn fordeling i klassen tilsvarer det ca 55 poeng. | |||
Median er ca. 55 poeng. | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 79: | Linje 91: | ||
===a)=== | ===a)=== | ||
Vi trenger to pinner | Vi trenger to pinner mer enn i figur tre, altså 9 pinner. | ||
Omkretsen av figur 4 er summen av lengdene til seks pinner, altså | Omkretsen av figur 4 er summen av lengdene til seks pinner, altså | ||
| Linje 86: | Linje 98: | ||
Vi setter figurnummer lik n. | Vi setter figurnummer lik n. | ||
Figur | Figur 1 har en mer enn det dobbelte av figurnummeret: 1 + 2 | ||
Figur 2: | Figur 2: 1 + 2 | ||
Figur 5: 1 | Figur 5: 1 + 2 | ||
Figur n: 2n+1. | Figur n: 1 + 2 | ||
Uttrykket vil atlså være 2n + 1. | |||
===c)=== | ===c)=== | ||
| Linje 102: | Linje 116: | ||
Finner antall pinner i omkretsen ved å dele på 2,5. | Finner antall pinner i omkretsen ved å dele på 2,5. | ||
$\frac{105}{2,5} = 42$ pinner | |||
Fra oppgave c ser man at det er snakk om figur nr. 40. Fra oppgave b finner man antall pinner totalt til å være 2n+1 = 81 pinner. | Fra oppgave c ser man at det er snakk om figur nr. 40. Fra oppgave b finner man antall pinner totalt til å være 2n+1 = 81 pinner. | ||
| Linje 118: | Linje 132: | ||
Vi ser ar f(1) er ca. - 40 cm (markert) og at f(12) er ca. 31 cm (ikke markert), fra | Vi ser ar f(1) er ca. - 40 cm (markert) og at f(12) er ca. 31 cm (ikke markert), fra figuren i a. | ||
===c)=== | ===c)=== | ||
Fra | Vi finner største forskjell ved å ta største verdi og trekke fra minste verdi. Fra figuren i a får vi da $59,72 - (-81,51) = 141,23$. Altså er det ca. 141 cm i forskjell mellom høyeste og laveste vannstand. | ||
===d)=== | ===d)=== | ||
Lager en tangent til grafen ved x=7. Fra den ser vi at den momentane veksten er 26,14cm/time. Det betyr at vannet stiger med en hastighet på ca. 26 cm/time kl 07:00. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 139: | Linje 153: | ||
Hun arvet 750 | Hun arvet 750 000 kroner. | ||
== Oppgave 4== | == Oppgave 4== | ||
| Linje 165: | Linje 179: | ||
Summerer | Summerer resultatene og deler på total frekvens (230). | ||
Gjennomsnitt= | Gjennomsnitt= | ||
Gjennomsnittet er ca 28,5. | Gjennomsnittet er ca. 28,5 poeng. | ||
==Oppgave 6== | ==Oppgave 6== | ||
| Linje 182: | Linje 196: | ||
===b)=== | ===b)=== | ||
Galdhøpiggen ligger 2 469 m - 1 106 m = 1 363 m over Spiterstulen. Temperaturen på Galdhøpiggen er altså 3,14 grader. (Pi grader ;-) ).Se figur i a. | |||
===c)=== | ===c)=== | ||
Endring per 100 meter stigning kan finnes fra figren over, eller ved regning: | |||
Temperaturen faller med 0,65 grader per 100 meter stigning, i følge modellen. | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 191: | Linje 211: | ||
[[File:2p17-7a2.png]] | [[File:2p17-7a2.png]] | ||
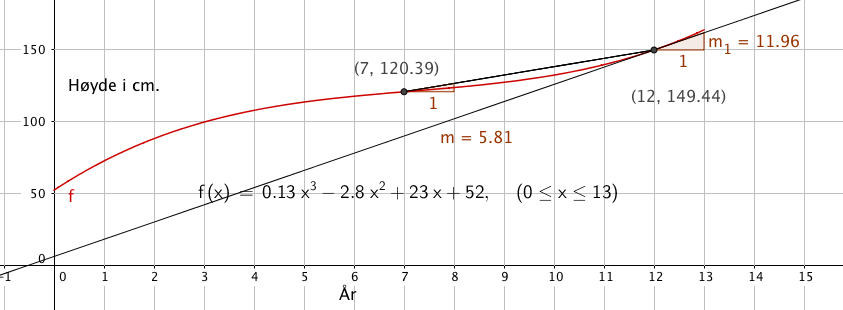
Bruker regresjonsanalyse i GeoGebra for å bestemme funksjonen. | |||
===b)=== | ===b)=== | ||
| Linje 200: | Linje 222: | ||
===c)=== | ===c)=== | ||
Modellen gir en momentan vekst på ca 12 cm ved tolv år. Etter det øker vekstem betydelig. Modellen er derfor ikke egnet til å vise | Modellen gir en momentan vekst på ca 12 cm ved tolv år. Etter det øker vekstem betydelig. Modellen er derfor ikke egnet til å vise Espens høyde etter fylte 12 år. | ||
==Oppgave 8== | ==Oppgave 8== | ||
| Linje 207: | Linje 229: | ||
===a)=== | ===a)=== | ||
Vi bruker 2P kalkulatoren til matematikk.net, se under | Vi bruker 2P kalkulatoren til matematikk.net, se under Ressurser. | ||
Liverpool FC: | Liverpool FC: | ||
| Linje 215: | Linje 237: | ||
Newcastle FC: | Newcastle FC: | ||
[[File:2p-17-813.png]] | |||
[[File:2p-17-812.png]] | [[File:2p-17-812.png]] | ||
| Linje 231: | Linje 256: | ||
==Oppgave 9== | ==Oppgave 9== | ||
===a)=== | |||
[[File:2p-17-2-9abc.png]] | |||
[[File:2p-17-2-9abc-2.png]] | |||
===b)=== | |||
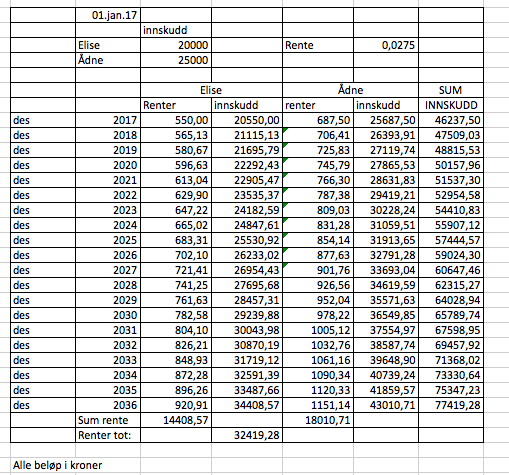
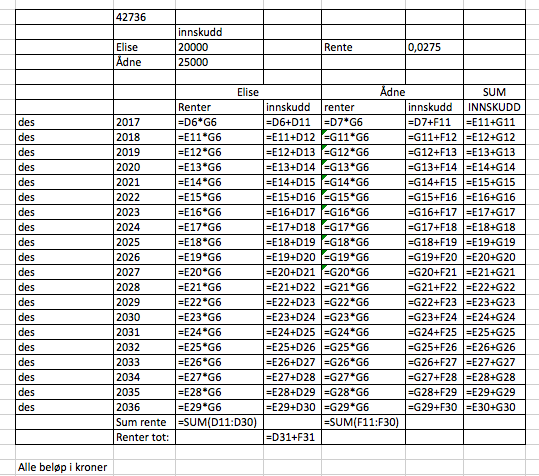
I desember 2033 passerer de 70 000 kroner i banken. Det er det 17 ende året. (se tab i a). | |||
===c)=== | |||
De vil få 32 419,28 kr. i renter til sammen. Se tabell i a. | |||
Siste sideversjon per 26. sep. 2017 kl. 19:48
Løsning bidratt av Lektor Ørjan Augedal, Fana privat gymnas
DEL EN
Oppgave 1
0,0,0,0,0,1,1,1,1,1,1,2,2,3,3,4
Variasjonsbredde: 4 -0 =4 ( største minus minste)
Typetall: 1 (den det er mest av)
Median 1 ( den i midten når materialet er organisert stigende)
Gjennomsnitt; Sum søsken delt påantall elever:
Oppgave 2
20% tok bussen den dagen.
Oppgave 3
Oppgave 4
I 10 liter vann, som er det samme som 100 dL vann er det ca.
For å finne antall molekyler i 1,5 dL, deler vi på 100 og ganger med 1,5:
Oppgave 5
a)
Dersom noe vokser periodisk med en fast størrelse har man en lineær sammenheng:
b)
Dersom noe vokser periodisk med en fast prosent er veksten eksponentiell. Vekstfaktoren her er 1,08:
c)
B er rettlinjet og KAN beskrive f.
A later til å være eksponentiell og KAN beskrive g.
Både A og C vokser, men ved eksponentiell positiv vekst vil den momentane veksten øke med tiden. Det er tillfelle i A. I graf C avtar den.
Oppgave 6
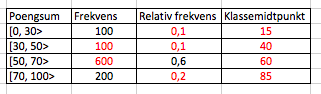
a)
b)
For å finne gjennomsnitt eller median må vi ANTA at verdiene er jevnt fordelt i hver klasse. Viktig å huske det når man bruker resultatene. De vil bare være sånn halveis gode, men det beste vi har og trolig gode nok.
Gjennomsnitt =
Gjennomsnittet er 58,5.
c)
Dersom det er medianeleven er 3525 : 2 = 1762,5, hvilket betyr at median er 1763. Vi ser at de ligger i klassen 50 - 70 poeng.
De to klassene før har 563 + 700 = 1263 elementer. Vi skal altså 500 elementer "inn" i 50- 70 klassen. Forutsatt jevn fordeling i klassen tilsvarer det ca 55 poeng.
Median er ca. 55 poeng.
Oppgave 7
a)
Vi trenger to pinner mer enn i figur tre, altså 9 pinner.
Omkretsen av figur 4 er summen av lengdene til seks pinner, altså
b)
Vi setter figurnummer lik n.
Figur 1 har en mer enn det dobbelte av figurnummeret: 1 + 2
Figur 2: 1 + 2
Figur 5: 1 + 2
Figur n: 1 + 2
Uttrykket vil atlså være 2n + 1.
c)
Omkretsen er hele tiden to mere enn figurnummeret. Altså n+2.
d)
Finner antall pinner i omkretsen ved å dele på 2,5.
Fra oppgave c ser man at det er snakk om figur nr. 40. Fra oppgave b finner man antall pinner totalt til å være 2n+1 = 81 pinner.
DEL TO
Oppgave 1
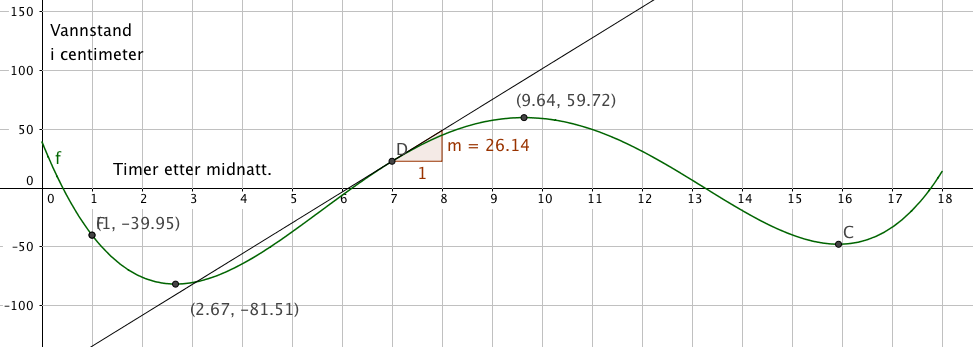
a)
b)
Vi ser ar f(1) er ca. - 40 cm (markert) og at f(12) er ca. 31 cm (ikke markert), fra figuren i a.
c)
Vi finner største forskjell ved å ta største verdi og trekke fra minste verdi. Fra figuren i a får vi da
d)
Lager en tangent til grafen ved x=7. Fra den ser vi at den momentane veksten er 26,14cm/time. Det betyr at vannet stiger med en hastighet på ca. 26 cm/time kl 07:00.
Oppgave 2
Prisantydning var på 3 220 000 kr.
Oppgave 3
Hun arvet 750 000 kroner.
Oppgave 4
Et legeme beveger seg med konstant hastighet bort fra utgangspunktet. Etter en stund beveger det seg tilbake til utgangspunktet med en konstant hastighet som er ca. dobbelt så stor som hastigheten bort fra utgangspunktet.
Oppgave 5
a)
Vi vet at søylehøyde er frekvens delt på klassebredde. Søylehøyden leser vi av i figuren. Vi har tre søyler og får:
Summen blir 230.
b)
Vi forutsetter at resultatene fordeler seg jevnt i hver klasse.
Multipliserer hvert enkelt klassemidtpunkt med respektive frekvens:
Summerer resultatene og deler på total frekvens (230).
Gjennomsnitt=
Gjennomsnittet er ca. 28,5 poeng.
Oppgave 6
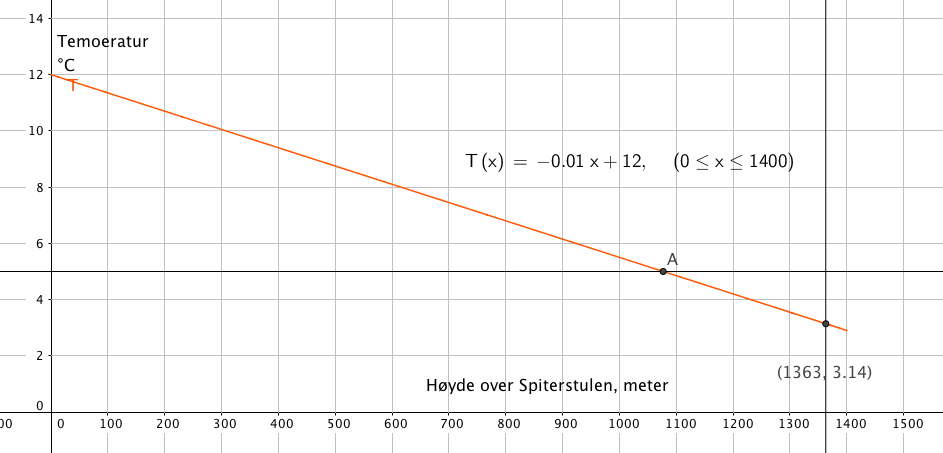
a)
Da er man ca. 1077 meter over Spiterstulen (A).
b)
Galdhøpiggen ligger 2 469 m - 1 106 m = 1 363 m over Spiterstulen. Temperaturen på Galdhøpiggen er altså 3,14 grader. (Pi grader ;-) ).Se figur i a.
c)
Endring per 100 meter stigning kan finnes fra figren over, eller ved regning:
Temperaturen faller med 0,65 grader per 100 meter stigning, i følge modellen.
Oppgave 7
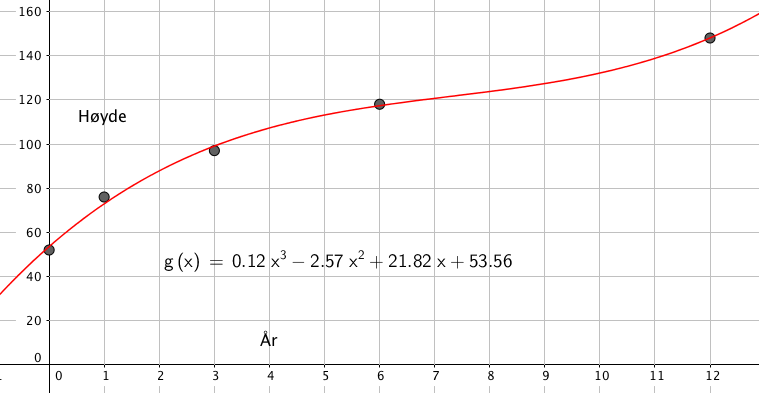
a)
Bruker regresjonsanalyse i GeoGebra for å bestemme funksjonen.
b)
Den gjennomsnittlige veksten er 5,8 cm per år, i tidsrommet 7 - 12 år.
c)
Modellen gir en momentan vekst på ca 12 cm ved tolv år. Etter det øker vekstem betydelig. Modellen er derfor ikke egnet til å vise Espens høyde etter fylte 12 år.
Oppgave 8
a)
Vi bruker 2P kalkulatoren til matematikk.net, se under Ressurser.
Liverpool FC:
Newcastle FC:
b)
Liverpool FC
Newcastle FC
Et lavt standardavvik betyr liten spredning rundt gjennomsnittet. Liverpool har et høyere standardavvik fordi de har flere kamper hvor de skårer mange mål.
Oppgave 9
a)
b)
I desember 2033 passerer de 70 000 kroner i banken. Det er det 17 ende året. (se tab i a).
c)
De vil få 32 419,28 kr. i renter til sammen. Se tabell i a.