1P 2016 vår LØSNING: Forskjell mellom sideversjoner
| (32 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 32: | Linje 32: | ||
==Oppgave 3== | ==Oppgave 3== | ||
2000 kr tilsvarer en indeks på 80. x tilsvarer en indeks på 60. Dersom det er | 2000 kr tilsvarer en indeks på 80. x tilsvarer en indeks på 60. Dersom det er samsvar mellom pris og indeks: | ||
$\frac{80}{60} = \frac{2000}{x} \\ 80x= 120000\\ x= 1500$ | $\frac{80}{60} = \frac{2000}{x} \\ 80x= 120000\\ x= 1500$ | ||
| Linje 54: | Linje 54: | ||
$y= kx \\ k= \frac yx$ | $y= kx \\ k= \frac yx$ | ||
k er den samme hele tiden og i dette | k er den samme hele tiden og i dette tilfellet blir $k = \frac{50}{2,5} = 20$ | ||
{| width="auto" | {| width="auto" | ||
| Linje 137: | Linje 137: | ||
===a)=== | ===a)=== | ||
Dette er et serielån. Fast avdrag hver termin og dyrest i starten av låneperioden. (Et | Dette er et serielån. Fast avdrag hver termin og dyrest i starten av låneperioden. (Et annuitetslån har et fast terminbeløp gjennom hele låneperioden). | ||
===b)=== | ===b)=== | ||
| Linje 181: | Linje 182: | ||
$O = 1200000 \cdot 1,035^{10} = 1 692 718,51$ | $O = 1200000 \cdot 1,035^{10} = 1 692 718,51$ | ||
Da vil | Da vil omsetningen være 1 692 719 kroner. | ||
===b)=== | ===b)=== | ||
| Linje 193: | Linje 194: | ||
===a)=== | ===a)=== | ||
{| width="auto" | |||
| | |||
|Sosialkunnskap | |||
|Ikke Sosialkunnskap | |||
|Total | |||
|- | |||
|Internasjonal engelsk | |||
|16 | |||
|0 | |||
|16 | |||
|- | |||
|Ikke Internasjonal engelsk | |||
|4 | |||
|6 | |||
|10 | |||
|- | |||
|Total | |||
|20 | |||
|6 | |||
|26 | |||
|} | |||
===b)=== | ===b)=== | ||
P ( sosialkunnskap, men ikke internasjonal engelsk) $= \frac{4}{26} = \frac{2}{13}$ | |||
Det er 2/13 sannsynlig at en tilfeldig utvalgt har Sosialkunnskap, men ikke Internasjonal engelsk. | |||
===c)=== | ===c)=== | ||
Alle som har valgt Internasjonal engelsk har også valgt Sosialkunnskap. Sannsynligheten er derfor 1, eller 100%. | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | ===a)=== | ||
Utbetalt: | |||
1996: 3 måneder, | |||
1997- 2013: $12 \cdot 17 = 204$ måneder, | |||
2014 : 8 måneder | |||
Totalt utbetalt: $215 \cdot 970= 208550$ kroner. | |||
===b)=== | ===b)=== | ||
Dersom indeksregulert: | |||
$\frac{970}{95,3} = \frac{x}{139,8} \Rightarrow x=14422,94 \approx 1423 $ kroner. | |||
===c)=== | ===c)=== | ||
[[File:1p-v16-2-5c.png]][[File:1p-v16-2-5c2.png]] | |||
Dersom barnetrygden hadde vært indeksregulert ville de fått utbetalt 255.346 kroner. | |||
==Oppgave 6== | ==Oppgave 6== | ||
===a)=== | ===a)=== | ||
[[File:1p-v16-2-6a.png]][[File:1p-v16-2-6a2.png]] | |||
===b)=== | ===b)=== | ||
Hun tar skattetrekk delt på bruttolønn og multipliserer med 100. Det gir gjennomsnittlig trekkprosent. | |||
[[File:1p-v16-2-6b1.png]][[File:1p-v16-2-6b2.png]] | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 216: | Linje 270: | ||
===b)=== | ===b)=== | ||
$\frac{26}{39} = \frac{CE}{36} \\ CE = 24$ | |||
Lengden av CE er 24. | |||
===c)=== | ===c)=== | ||
| Linje 223: | Linje 282: | ||
Forholdet mellom arealene av trekantene blir da: | Forholdet mellom arealene av trekantene blir da: | ||
$\frac{\triangle {ABC}}{\triangle CED}$ | $\frac{\triangle {ABC}}{\triangle CED} = \frac{\frac 12 \cdot \frac 32 \cdot \frac 32}{\frac 12 \cdot 1 \cdot 1} = \frac 94$ | ||
==Oppgave 8== | ==Oppgave 8== | ||
===a)=== | ===a)=== | ||
$V= \pi r^2 \cdot 2 \pi R \\ V= 2 \pi^2\cdot (5,1cm)^2 \cdot 20,4 cm \\ V = 10473,7 cm^3 = 10,474$ | |||
Volumet er 10,474 liter. | |||
===b)=== | ===b)=== | ||
For å finne den indre radius (AB) må vi først finne r, siden AB = R - r. | |||
$ r = \big | \sqrt{\frac{V}{2\pi^2 R}} \big | \\ r = \big | \sqrt{\frac{8600cm^3}{2\pi^2 \cdot 10,2 cm}} \big | =3,6644 cm $ | |||
Da blir AB = 10,2 cm - 6,53 cm = 3,67 cm | |||
Omkrets av sirkel med radius AB blir da : $O= 2\pi \cdot (AB) = 23,0 cm$ | |||
Siste sideversjon per 13. sep. 2016 kl. 15:34
Løsning laget av mattepratbruker Dolandyret
DEL EN
Oppgave 1
a)
Økning i prosentpoeng: 4,5 - 3,6 = 0.9
Økningen var på 0,9 prosentpoeng.
b)
$\frac{0,9}{3,6} = \frac {9}{36} = \frac {3}{12} = 25$%
Økningen var på 25%.
Oppgave 2
Volum prisme:
$V= b\cdot h \cdot l = \\ V= 40 \cdot 90 \cdot 30 \cdot cm ^3 = \\ v= 108000 cm^3 = \\ 108 dm^3= \\ 108 liter.$
Tanken rommer 108 liter.
Oppgave 3
2000 kr tilsvarer en indeks på 80. x tilsvarer en indeks på 60. Dersom det er samsvar mellom pris og indeks:
$\frac{80}{60} = \frac{2000}{x} \\ 80x= 120000\\ x= 1500$
I 2016 ville varen kostet 1500 kroner, dersom den følger indeksen.
Oppgave 4
$240 km = 240000m = 2400000dm = 24000000cm$
Målestokk: $\frac{12}{24000000}= \frac{1}{2000000}$
Målestokken er 1: 2 000 000.
Oppgave 5
For proporsjonale størrelser gjelder :
$y= kx \\ k= \frac yx$
k er den samme hele tiden og i dette tilfellet blir $k = \frac{50}{2,5} = 20$
| x | 2,5 | 7,5 | 10 |
| y | 50 | 150 | 200 |
Oppgave 6
a)
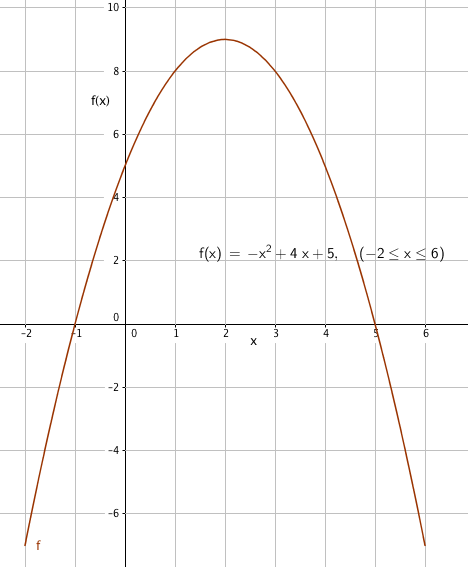
$f(x)= -x^2 +4x+5$
| x | $-2$ | $-1$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | $-7$ | 0 | 5 | 8 | 9 | 8 | 5 | 0 | $-7$ |
b)
Oppgave 7
a)
Tre blå: $P(tre blå)= \frac{6}{10} \cdot \frac{5}{9} \cdot \frac {4}{8} = \frac 16 $
b)
Det "motsatte" av minst en rosa er ingen rosa, altså bare blå, som vi fant sannsynligheten for i a. Vi får da:
P( minst en rosa)=$ 1- \frac{1}{6} =\frac56$
c)
Den rosa ballongen kan trekkes første, andre eller tredje gang:
P(en rosa)= $\frac{4}{10} \cdot \frac{6}{9} \cdot \frac{5}{8} +\frac{6}{10} \cdot \frac{4}{9} \cdot \frac{5}{8} + \frac{6}{10} \cdot \frac{5}{9} \cdot \frac{4}{8} = \frac 12 $
Oppgave 8
a)
Man ser at når antall bilder øker fra 8 til 14, altså med 6, øker prisen med 300 kroner. Prisen per bilde blir 50 kroner. Dette stemmer også med økningen fra 14 til 24.
8 bildet koster 400 kroner, det betyr at boken uten bilder koster 600 kroner. Vi får:
y = 50x + 600
b)
a = 50 kroner, altså prisen per bilde (stigningstallet).
b = 600 kroner, pris på bok uten bilder (konstantleddet).
Oppgave 9
a)
Dette er et serielån. Fast avdrag hver termin og dyrest i starten av låneperioden. (Et annuitetslån har et fast terminbeløp gjennom hele låneperioden).
b)
Summerer vi alle avdragene ser man at lånesummen er 100.000 kroner. Det første året betaler hun 4000 kroner i rente. Den årlige renter er derfor 4%.
Oppgave 10
Bruker pytagoras og finner at AC = 6.
Areal av grå halvsirkel: $A= \frac{\pi r^2}{2} = \frac{25 \pi}{2}$
Sum av areal av grønn og blå halvsirkel:$A= \frac{16 \pi }{2} + \frac{9 \pi}{2}= \frac{25 \pi}{2}$
DEL TO
Oppgave 1
a)
b)
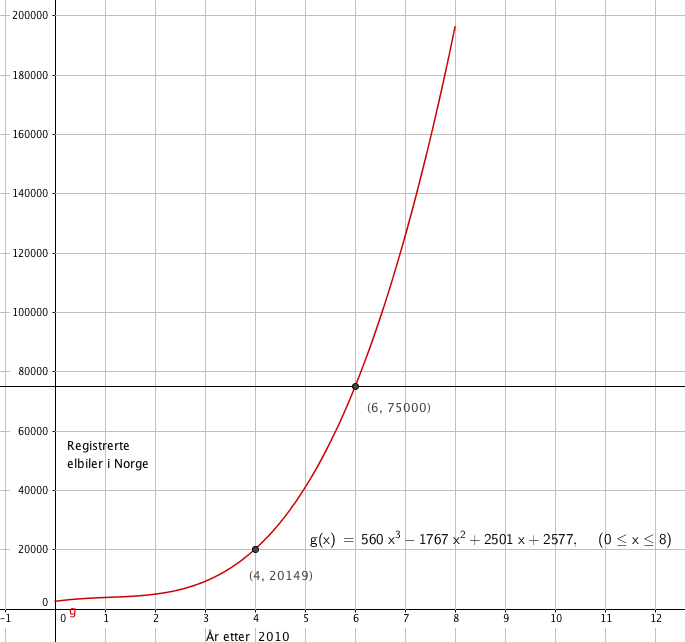
Det skjer i 2016, i følge modellen.
c)
g(4) forteller oss at i 2014 var det 20149 registrerte elbiler i Norge. (se figur i a).
Oppgave 2
Dersom kjøpekraften skal opprettholdes må lønnsutviklingen følge konsumprisindeksen:
$ \frac{450000}{128,8} = \frac{x}{139,8} \\ x= \frac{450000 \cdot 139,8}{128,8} \\ x= 488431,68$
Han må ha en lønn på 488 432 for å opprettholde kjøpekraften i 2015, i forhold til 2010.
Oppgave3
a)
$O = 1200000 \cdot 1,035^{10} = 1 692 718,51$
Da vil omsetningen være 1 692 719 kroner.
b)
$x \cdot 1,4 \cdot 0,8 \cdot 0,8 = 560 \\ 0,896x =560 \\ x = 625$
Produktet koster 625 kroner før endringene.
Oppgave 4
a)
| Sosialkunnskap | Ikke Sosialkunnskap | Total | |
| Internasjonal engelsk | 16 | 0 | 16 |
| Ikke Internasjonal engelsk | 4 | 6 | 10 |
| Total | 20 | 6 | 26 |
b)
P ( sosialkunnskap, men ikke internasjonal engelsk) $= \frac{4}{26} = \frac{2}{13}$
Det er 2/13 sannsynlig at en tilfeldig utvalgt har Sosialkunnskap, men ikke Internasjonal engelsk.
c)
Alle som har valgt Internasjonal engelsk har også valgt Sosialkunnskap. Sannsynligheten er derfor 1, eller 100%.
Oppgave 5
a)
Utbetalt:
1996: 3 måneder, 1997- 2013: $12 \cdot 17 = 204$ måneder, 2014 : 8 måneder
Totalt utbetalt: $215 \cdot 970= 208550$ kroner.
b)
Dersom indeksregulert:
$\frac{970}{95,3} = \frac{x}{139,8} \Rightarrow x=14422,94 \approx 1423 $ kroner.
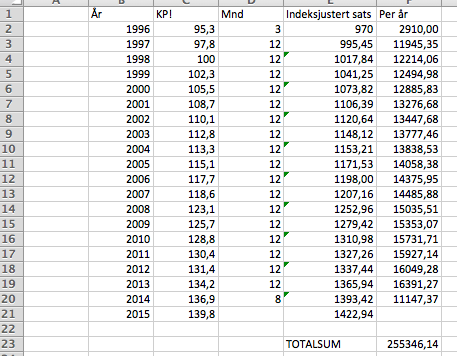
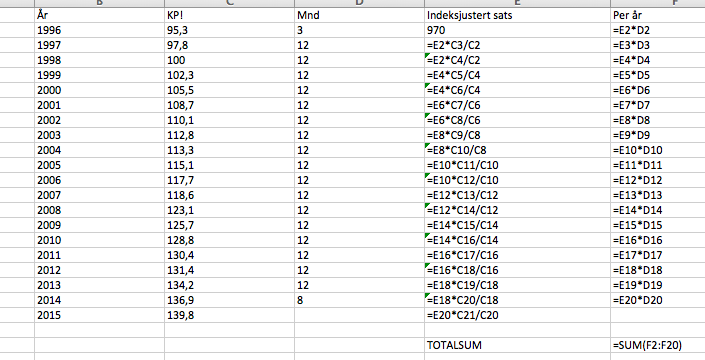
c)
Dersom barnetrygden hadde vært indeksregulert ville de fått utbetalt 255.346 kroner.
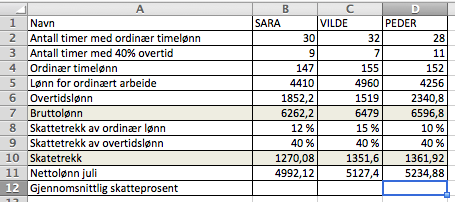
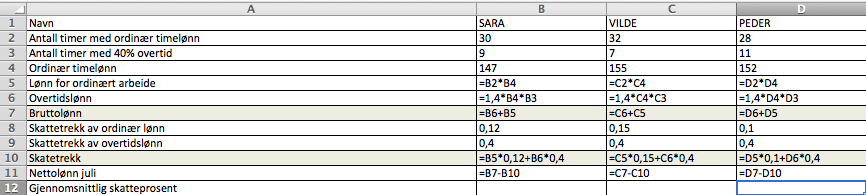
Oppgave 6
a)
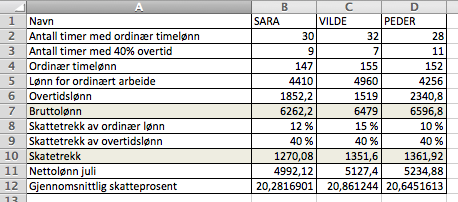
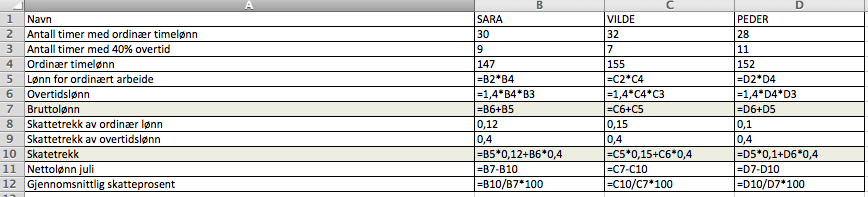
b)
Hun tar skattetrekk delt på bruttolønn og multipliserer med 100. Det gir gjennomsnittlig trekkprosent.
Oppgave 7
a)
Trekantene er formlike fordi vinklene er parvis like. Vinkel C er felles i begge. Begge har en rett vinkel. Vinkel A er da like stor som vinkel D i trekanten CED.
b)
$\frac{26}{39} = \frac{CE}{36} \\ CE = 24$
Lengden av CE er 24.
c)
Forholdet mellom sidene i trekantene er $\frac{39}{26} = \frac 32$
Forholdet mellom arealene av trekantene blir da:
$\frac{\triangle {ABC}}{\triangle CED} = \frac{\frac 12 \cdot \frac 32 \cdot \frac 32}{\frac 12 \cdot 1 \cdot 1} = \frac 94$
Oppgave 8
a)
$V= \pi r^2 \cdot 2 \pi R \\ V= 2 \pi^2\cdot (5,1cm)^2 \cdot 20,4 cm \\ V = 10473,7 cm^3 = 10,474$
Volumet er 10,474 liter.
b)
For å finne den indre radius (AB) må vi først finne r, siden AB = R - r.
$ r = \big | \sqrt{\frac{V}{2\pi^2 R}} \big | \\ r = \big | \sqrt{\frac{8600cm^3}{2\pi^2 \cdot 10,2 cm}} \big | =3,6644 cm $
Da blir AB = 10,2 cm - 6,53 cm = 3,67 cm
Omkrets av sirkel med radius AB blir da : $O= 2\pi \cdot (AB) = 23,0 cm$