R1 2013 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (38 mellomliggende versjoner av 4 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://matematikk.net/ | {{EksLenker|1= | ||
*[http://matematikk.net/res/eksamen/R1/R1_H13.pdf Oppgaven som pdf] | |||
*[http://udl.no/r1-matematikk/r1-eksamen-host-2013 Løsning som video fra UDL.no] | |||
*[http://ndla.no/nb/node/138584?fag=57933 Løsning fra NDLA] | |||
* [http://matematikk.net/matteprat/viewtopic.php?f=13&t=36386 Matteprat: Diskusjon omkring denne oppgaven] | |||
*[http://www.matematikk.net/res/eksamen/R1/sensur/2013H_Vurderingsskjema_REA3022_MatematikkR1_H13.pdf Vurderingsskjema] | |||
*[http://www.matematikk.net/res/eksamen/R1/sensur/2013H_Sensorveiledning_REA3022_MatematikkR1_H13.pdf Sensorveiledning] | |||
}} | |||
| Linje 9: | Linje 15: | ||
===a)=== | ===a)=== | ||
$f(x) = 2e^{3x} \\ | $f(x) = 2e^{3x} \\ f'(x) = 2(3x)'e^{3x} = 6e^{3x}$ | ||
===b)=== | ===b)=== | ||
$g(x) = 2x \cdot \ln(3x) \\ | $g(x) = 2x \cdot \ln(3x) \\ g'(x) = 2 ln(3x) + 2x \cdot \frac{1}{3x} \cdot (3x)' \\ g'(x) = 2( \ln(3x)+1)$ | ||
===c)=== | ===c)=== | ||
$h(x)= \frac {2x-1}{x+1} \\ | $h(x)= \frac {2x-1}{x+1} \\ h'(x) = \frac{2(x+1) - (2x-1)}{(x+1)^2} \\ h'(x) = \frac {3}{(x+1)^2} $ | ||
==Oppgave 2:== | ==Oppgave 2:== | ||
| Linje 43: | Linje 50: | ||
*Avsett linjestykket AB lik 10 cm | *Avsett linjestykket AB lik 10 cm | ||
*Konstruer en halvsirkel med diameter 10 cm, med sentrum midt mellom A og B. | *Konstruer en halvsirkel med diameter 10 cm, med sentrum midt mellom A og B. | ||
*Konstruere en linje | *Konstruere en linje parallell med AB, med avstand 4 cm. Denne linjen skjærer halvsirkelen i to punkter. | ||
[[File:3-r1-h2013.png]] | [[File:3-r1-h2013.png]] | ||
| Linje 93: | Linje 100: | ||
$S_2 : (x-a)^2+y^2=9$ Setter a=6. Sirkelen | $S_2 : (x-a)^2+y^2=9$ Setter a = 6. Sirkelen har sentrum i (6, 0) og radius 3 | ||
| Linje 100: | Linje 107: | ||
===b)=== | ===b)=== | ||
$S_2$ kan tangere $S_1$ både utvendig og | $S_2$ kan tangere $S_1$ både utvendig og innvendig. Det er bare forskyvning i x rettning, og det finnes fire muligheter. | ||
$a = \pm r_2 \pm r_1 \\ a = \pm 5 \pm 3 \\ a=-8 \vee a= -2 \vee a= 2 \vee a= 8$ | $a = \pm r_2 \pm r_1 \\ a = \pm 5 \pm 3 \\ a=-8 \vee a= -2 \vee a= 2 \vee a= 8$ | ||
| Linje 124: | Linje 131: | ||
===c)=== | ===c)=== | ||
$ (x-2)^2 (x+2) = \\(x^2-4x+4)(x^2+4x+4)$ | $ (x-2)^2 (x+2)^2 = \\(x^2-4x+4)(x^2+4x+4)$ | ||
Man observerer at konstantleddet i uttrykket over | Man observerer at konstantleddet i uttrykket over blir 16. h skjærer y-aksen i 8, man må derfor multiplisere med en halv. h(x) blir da: | ||
$h(x) = \frac 12 (x-2)^2(x+2)^2$ | $h(x) = \frac 12 (x-2)^2(x+2)^2$ | ||
| Linje 172: | Linje 179: | ||
===b)=== | ===b)=== | ||
Vi har | Vi har sirkellikningen: $x^2 + y^2 = r^2$ | ||
Dersom vinkel APB er nitti grader, må vektorene PA og PB stå normalt på hverandre. Da er skalarproduktet av vektorene null. | Dersom vinkel APB er nitti grader, må vektorene PA og PB stå normalt på hverandre. Da er skalarproduktet av vektorene null. | ||
| Linje 215: | Linje 222: | ||
$ \vec{AB} = [6,4] \\ \vec{AD} = [1,5] \\ | \vec{AB}| = \sqrt{36+16} = \sqrt {52} \\ |\vec{AD}| = \sqrt{25+1} = \sqrt{26} \\ \vec {AB} \cdot \vec{AD} = | \vec{AB} | \cdot | \vec{AD} | \cdot \cos (BAD) \\ \cos(BAD) = \frac { \vec {AB} \cdot \vec{AD}}{| \vec{AB} | \cdot | \vec{AD}| } \\ \cos (BAD) = \frac{[6,4] \cdot [1,5]}{\sqrt {52} \cdot \sqrt{26}} \\ \cos (BAD) = \frac{26}{ \sqrt{26 \cdot 26 \cdot 2}} \\ \cos(BAD)= \frac {\sqrt 2}{2}$ | $ \vec{AB} = [6,4] \\ \vec{AD} = [1,5] \\ | \vec{AB}| = \sqrt{36+16} = \sqrt {52} \\ |\vec{AD}| = \sqrt{25+1} = \sqrt{26} \\ \vec {AB} \cdot \vec{AD} = | \vec{AB} | \cdot | \vec{AD} | \cdot \cos (BAD) \\ \cos(BAD) = \frac { \vec {AB} \cdot \vec{AD}}{| \vec{AB} | \cdot | \vec{AD}| } \\ \cos (BAD) = \frac{[6,4] \cdot [1,5]}{\sqrt {52} \cdot \sqrt{26}} \\ \cos (BAD) = \frac{26}{ \sqrt{26 \cdot 26 \cdot 2}} \\ \cos(BAD)= \frac {\sqrt 2}{2}$ | ||
Vinkel (BAD) = $ \cos^{-1} (\frac{\sqrt 2}{2} =45^{\circ}$ | Vinkel (BAD) = $ \cos^{-1} (\frac{\sqrt 2}{2} ) =45^{\circ}$ | ||
Areal av trekanten; | |||
$A = \frac 12 | \vec{AB} | \cdot | \vec{AD} | \sin(BAD) = \frac 12 \cdot \sqrt{26} \cdot \sqrt{26 \cdot 2} \cdot \frac{\sqrt{2} }{2} =13 $ | |||
===b)=== | ===b)=== | ||
$\vec{DC} || \vec {AB} , \quad \quad D (x,y) \\ k \vec{DC} = \vec{AB} \\ k[x+2, y-2] = [6,4] \\ kx+2k=6 \wedge ky-2k = 4 \\ x = \frac{6-2k}{k} \wedge y = \frac{4+2k}{k}$ | |||
Skalarproduktet mellom AB og BC vektor er null. | |||
$[6,4] \cdot [x-3, y-1] = 0 \\ 6x -18 + 4y -4 = 0 \\ 6x-4y - 22 =0 \\ 6 ( \frac{6-2k}{k}) + 4(\frac{4+2k}{k}) -22 =0 \\ \frac{52}{k} = 26 \\ k =2$ | |||
Setter inn i uttrykkene for x og y: | |||
$ x = \frac{6-2k}{k} \wedge y = \frac{4+2k}{k} \\ x = \frac{6-2 \cdot 2}{2} \wedge y = \frac{4+2\cdot 2}{2 } \\ x= 1 \wedge y = 4 $ | |||
Dvs. C (1, 4) | |||
===c)=== | ===c)=== | ||
E ( s, 2s-2) | |||
$x= -2+3t \wedge y = 2+2t \\ s = -2+3t \wedge 2s-2 = 2+2t \\ 2(-2+3t) - 2 =2+2t \\ -4+ 4t = 4 \\ t= 2 \\ x = -2+6 \wedge y = 2+4 \\ x=4 \wedge y= 6$ | |||
Dvs, s = 4 | |||
[[File:6c-r1-h2014.png]] | |||
E (4, 6) | |||
===d)=== | ===d)=== | ||
Dersom E skal ligge på l og AE vektor være like lang som BE vektor, ser man fra figuren over at E må sammenfalle med D, altså må E ha koordinatene (-2, 2) | |||
Ved regning: | |||
$\vec{AE} = [3t+1, 2t+5] \\ \vec{BE} = [3t-5, 2t+1] \\ |\vec{AE}| = |\vec{AB}| \\ \sqrt{(3t+1)^2 + (2t+5)^2} = \sqrt{(3t-5)^2 +(2t-1)^2 } \\ t=0$ | |||
Innsatt i parameterfremstillingen for l gir det (-2, 2) som er sammenfallende med D. | |||
==Oppgave 7== | ==Oppgave 7== | ||
Siste sideversjon per 15. feb. 2016 kl. 14:24
DEL EN
Oppgave 1:
a)
$f(x) = 2e^{3x} \\ f'(x) = 2(3x)'e^{3x} = 6e^{3x}$
b)
$g(x) = 2x \cdot \ln(3x) \\ g'(x) = 2 ln(3x) + 2x \cdot \frac{1}{3x} \cdot (3x)' \\ g'(x) = 2( \ln(3x)+1)$
c)
$h(x)= \frac {2x-1}{x+1} \\ h'(x) = \frac{2(x+1) - (2x-1)}{(x+1)^2} \\ h'(x) = \frac {3}{(x+1)^2} $
Oppgave 2:
a)
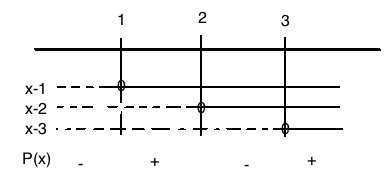
$P(x)= x^3-6x^2+11x-6 \\ P(1)= 1^3 - 6 \cdot 1^2 + 11 \cdot 1 -6 =0$
b)
$ \quad( x^3-6x^2+11x-6) : (x-1) =x^2 - 5x + 6\\ -(x^3 -x^2) \\ \quad \quad -5x^2 \\ \quad \quad -(-5x^2 +5x) \\ \quad \quad \quad \quad \quad \quad 6x-6$
$x^2-5x+6=0 \\ x= \frac{5 \pm \sqrt{25-24}}{2} \\ x= 2 \vee x=3$
$P(x)=x^3-6x^2+11x-6 = (x-1)(x-2)(x-3)$
$P(x) \geq 0$
$x \in [1,2] \cup [3, \rightarrow>$
Oppgave 3:
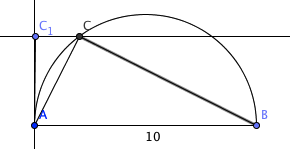
- Avsett linjestykket AB lik 10 cm
- Konstruer en halvsirkel med diameter 10 cm, med sentrum midt mellom A og B.
- Konstruere en linje parallell med AB, med avstand 4 cm. Denne linjen skjærer halvsirkelen i to punkter.
Oppgave 4:
$2^{3x-1} = 2^2+2^2+2^2+2^2 \\ 2^{3x+1} = 4 \cdot 2^2 \\ 2^{3x-1} = 2^4 \\3x-1 =4 \\ x = \frac 53$
Oppgave 5:
a)
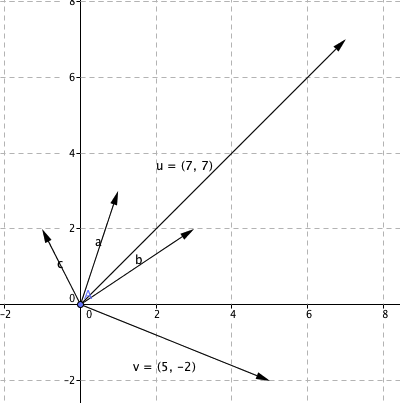
b)
$\vec u \cdot \vec v = [7,7] \cdot [5, -2] = 5\cdot 7 + (-2) \cdot 7 = 35-14 =21$
Vektorene u og v står ikke vinkelrett på hverandre.
Oppgave 6:
a)
$f(x)= - \frac 13 x^3+2x^2, \quad D_f \in \R \\ f´(x)= -x^2 +4x \\ f´´(x) = -2x+4$
b)
Ekstremalpunkter:
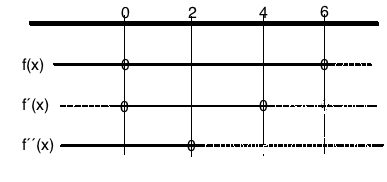
$f ´(x)=0 \\ -x^2+4x=0 \\ x(-x+4)=0 \\ x=0 \vee x= 4 \\ f(0) = 0 \wedge f(4) = \frac{32}{3} \\ (0,0) \wedge ( 4, \frac{32}{3})$
Vendepunkt:
$f´´(x)=0 \\ -2x+4 =0 \\ x= 2 \\ f(2) = - \frac {8}{3} + \frac{24}{3} = \frac {16}{3} \\ (2, \frac{16}{3})$
Fortegnslinjer:
c)
Oppgave 7:
a)
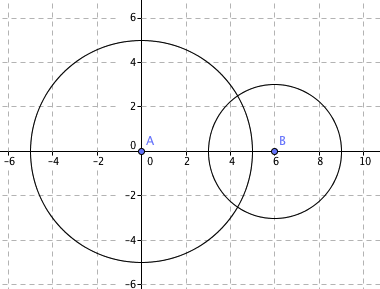
$S_1 : x^2+y^2=25$ Sirkelen har sentrum i origo og radius 5
$S_2 : (x-a)^2+y^2=9$ Setter a = 6. Sirkelen har sentrum i (6, 0) og radius 3
b)
$S_2$ kan tangere $S_1$ både utvendig og innvendig. Det er bare forskyvning i x rettning, og det finnes fire muligheter.
$a = \pm r_2 \pm r_1 \\ a = \pm 5 \pm 3 \\ a=-8 \vee a= -2 \vee a= 2 \vee a= 8$
DEL TO
Oppgave 1
a)
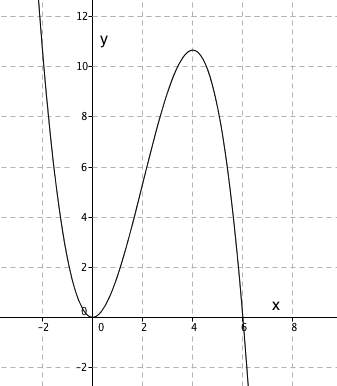
Grafen tangerer x- aksen for x=2, derfor $(x-2)^2$
$f(x) = 2(x-2)^2 = 2(x^2-4x+4 )= 2x^2-8x+8$
Man observer at konstantleddet 8 stemmer med grafen skjæring med y aksen. Uttrykket for f(x) er derfor riktig.
b)
$(x-3)^2(x+1) = x^3-5x^2-6x+9$
Man observerer at g skjærer y-aksen i 9, dvs. k = 1.
c)
$ (x-2)^2 (x+2)^2 = \\(x^2-4x+4)(x^2+4x+4)$
Man observerer at konstantleddet i uttrykket over blir 16. h skjærer y-aksen i 8, man må derfor multiplisere med en halv. h(x) blir da:
$h(x) = \frac 12 (x-2)^2(x+2)^2$
Oppgave 2
a)
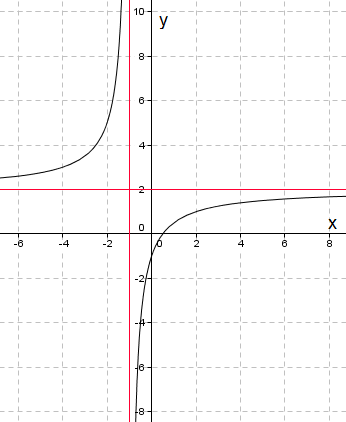
Asymptoter:
Horisontal: $ lim_{x \to \pm \infty} f(x)= lim_{x \to \pm \infty} \frac {2x-1}{x+1} = lim_{x \to \pm \infty} \frac {\frac {2x}{x}- \frac1x}{\frac xx+ \frac 1x} =2 $
Vertikal: x + 1 = 0, x = -1
b)
$f(x)=g(x) \\ \frac{2x-1}{x+1} = x-1 \\ 2x-1 = x^2-1 \\ x^2-2x=0 \\x=0 \vee x=2$
Oppgave 3
a)
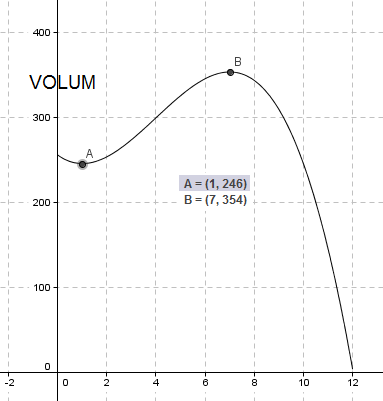
Areal av rektangel;
$A = b \cdot h \\ A= (12-x) \cdot f(x) \\ A= (12-x) \cdot (x^2+21) \\ A = 12x^2-3x^3+252-21x \\ A(x)= -x^3+12x^2-21x + 252$
b)
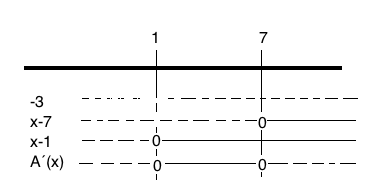
$A(x)= -x^3+12x^2-21x + 252 \\ A´(x) = -3x^2+24x-21 \\ x= \frac {-24 \pm \sqrt{24^2 -4 \cdot (-3) \cdot (-21)}}{-6} \\x=1 \vee x=7 $
c)
Oppgave 4
a)
$A = (-r, 0) \\ B = (r,0)$
$\vec{PA} = [-r-x, -y] \\ \vec {PB} = [r-x, -y]$
b)
Vi har sirkellikningen: $x^2 + y^2 = r^2$
Dersom vinkel APB er nitti grader, må vektorene PA og PB stå normalt på hverandre. Da er skalarproduktet av vektorene null.
$[ -r-x, -y] \cdot [r-x, -y] = -r^2 +rx -rx +x^2 +y^2 \\ x^2 + y^2-r^2 =0$
Som vi viste på forhånd (sentralvinkel / periferivinkel) er vinkelen 90 grader.
Oppgave 5
a)
Sannsynlighet for matematikk og fysikk:
$P(M \cap F) = P(M) + P(F) - P(M \cup F) = 0,64 + 0,32 - 0,70 = 0,26$
Sannsynlighet for matematikk og ikke fysikk:
$P(M\cap \overline F) = P(M) - P(M \cap F) = 0,64 - 0,26 = 0,38$
b)
Sannsynlighet for fysikk, gitt matematikk:
$P(F | M) = \frac{P(F \cap M)}{P(M)} = \frac{0,26}{0,64} =0,41 $
Nei, hendelsenne er avhengige fordi $P(F) \neq P(F|M)$.
c)
Sannsynligheten for matematikk, gitt fysikk;
$P(M | F ) = \frac{P(F | M ) \cdot P(M)}{P(F)} = \frac {0,41 \cdot 0,64}{0,32} = 0,82$
Oppgave 6
a)
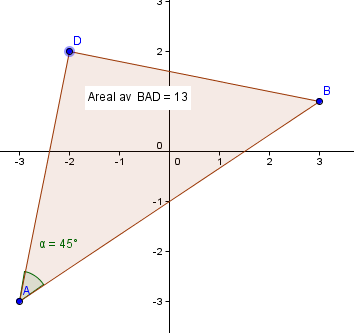
$ \vec{AB} = [6,4] \\ \vec{AD} = [1,5] \\ | \vec{AB}| = \sqrt{36+16} = \sqrt {52} \\ |\vec{AD}| = \sqrt{25+1} = \sqrt{26} \\ \vec {AB} \cdot \vec{AD} = | \vec{AB} | \cdot | \vec{AD} | \cdot \cos (BAD) \\ \cos(BAD) = \frac { \vec {AB} \cdot \vec{AD}}{| \vec{AB} | \cdot | \vec{AD}| } \\ \cos (BAD) = \frac{[6,4] \cdot [1,5]}{\sqrt {52} \cdot \sqrt{26}} \\ \cos (BAD) = \frac{26}{ \sqrt{26 \cdot 26 \cdot 2}} \\ \cos(BAD)= \frac {\sqrt 2}{2}$
Vinkel (BAD) = $ \cos^{-1} (\frac{\sqrt 2}{2} ) =45^{\circ}$
Areal av trekanten;
$A = \frac 12 | \vec{AB} | \cdot | \vec{AD} | \sin(BAD) = \frac 12 \cdot \sqrt{26} \cdot \sqrt{26 \cdot 2} \cdot \frac{\sqrt{2} }{2} =13 $
b)
$\vec{DC} || \vec {AB} , \quad \quad D (x,y) \\ k \vec{DC} = \vec{AB} \\ k[x+2, y-2] = [6,4] \\ kx+2k=6 \wedge ky-2k = 4 \\ x = \frac{6-2k}{k} \wedge y = \frac{4+2k}{k}$
Skalarproduktet mellom AB og BC vektor er null.
$[6,4] \cdot [x-3, y-1] = 0 \\ 6x -18 + 4y -4 = 0 \\ 6x-4y - 22 =0 \\ 6 ( \frac{6-2k}{k}) + 4(\frac{4+2k}{k}) -22 =0 \\ \frac{52}{k} = 26 \\ k =2$
Setter inn i uttrykkene for x og y:
$ x = \frac{6-2k}{k} \wedge y = \frac{4+2k}{k} \\ x = \frac{6-2 \cdot 2}{2} \wedge y = \frac{4+2\cdot 2}{2 } \\ x= 1 \wedge y = 4 $
Dvs. C (1, 4)
c)
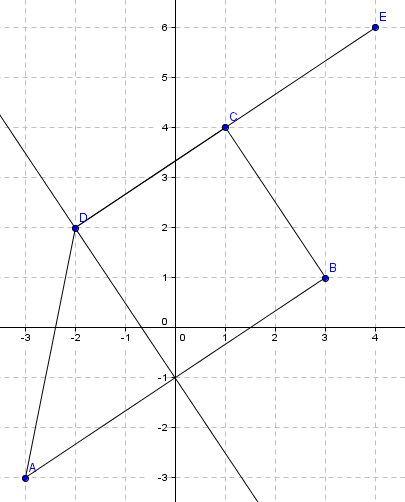
E ( s, 2s-2)
$x= -2+3t \wedge y = 2+2t \\ s = -2+3t \wedge 2s-2 = 2+2t \\ 2(-2+3t) - 2 =2+2t \\ -4+ 4t = 4 \\ t= 2 \\ x = -2+6 \wedge y = 2+4 \\ x=4 \wedge y= 6$
Dvs, s = 4
E (4, 6)
d)
Dersom E skal ligge på l og AE vektor være like lang som BE vektor, ser man fra figuren over at E må sammenfalle med D, altså må E ha koordinatene (-2, 2)
Ved regning:
$\vec{AE} = [3t+1, 2t+5] \\ \vec{BE} = [3t-5, 2t+1] \\ |\vec{AE}| = |\vec{AB}| \\ \sqrt{(3t+1)^2 + (2t+5)^2} = \sqrt{(3t-5)^2 +(2t-1)^2 } \\ t=0$
Innsatt i parameterfremstillingen for l gir det (-2, 2) som er sammenfallende med D.
Oppgave 7
$n^2 \cdot (\frac{x}{n})^{ln(x) - 2} = x^2 \quad x> 0 \wedge n>0 \\ (\frac{x}{n})^{ln(x) - 2} = (\frac{x}{n})^2 \\ ln(x) =4 \\ x= 10 000 $
Når x er lik n er brøken lik en og likningen stemmer. Derfor er x = n også en løsning av likningen. Dvs:
x = 10 000 eller x = n.