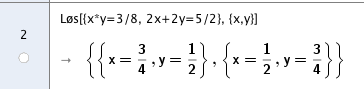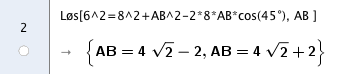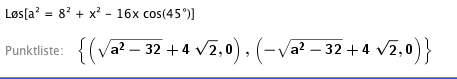1T 2015 høst LØSNING: Forskjell mellom sideversjoner
| (42 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 19: | Linje 19: | ||
<math> \left[ \begin{align*}-4x-6y = -26 \\ 4x-2y=2 \end{align*}\right] </math> | <math> \left[ \begin{align*}-4x-6y = -26 \\ 4x-2y=2 \end{align*}\right] </math> | ||
Legger sammen | Legger sammen likningene og x forsvinner: | ||
<math> \left[ \begin{align*}-8y= -24 \end{align*}\right] </math> | <math> \left[ \begin{align*}-8y= -24 \end{align*}\right] </math> | ||
Det gir y = 3. Innsatt i en av | Det gir y = 3. Innsatt i en av likningene gir det x = 2. Løsning er altså $x=2 \wedge y=3$ | ||
===Oppgave 3=== | ===Oppgave 3=== | ||
| Linje 87: | Linje 87: | ||
===b)=== | ===b)=== | ||
Koeffisienten foran andregradsleddet er positiv, det betyr at grafen vender sin hule side opp, og har et minimumspunkt. Dette ligger på symmetrilinja som er x= 0,5. | |||
| Linje 160: | Linje 160: | ||
===b)=== | ===b)=== | ||
P(pos | smittet) = $\frac{58}{60} = \frac{29}{30}$ | P( pos | smittet) = $\frac{58}{60} = \frac{29}{30}$ | ||
===c)=== | ===c)=== | ||
P( ikke smittet | pos test) = $\frac{10}{68} = \frac{5}{34}$ | |||
===Oppgave 13=== | ===Oppgave 13=== | ||
| Linje 176: | Linje 178: | ||
$Sin B = \frac{h}{20} \\ \frac{3}{5} = \frac{h}{20} \\ h = 12$ | $Sin B = \frac{h}{20} \\ \frac{3}{5} = \frac{h}{20} \\ h = 12$ | ||
Bruker | Bruker Pytagoras to ganger, for å finne grunnlinja AB: | ||
AB = AD + DB = $\sqrt{13^2 - 12^2} + \sqrt{20^2-12^2} = 5+16= 21$ | |||
Areal: $A= \frac{21 \cdot 12}{2} = 126$ | |||
==DEL TO== | ==DEL TO== | ||
| Linje 196: | Linje 201: | ||
===Oppgave 2=== | ===Oppgave 2=== | ||
[[File:1t-h2015-22.png]] | |||
De tre skraverte trekantene har samme areal (selv om det ikke ser slik ut :-)) | |||
Setter arealet av den likebeinte skraverte trekanten lik arealet til en av de andre skraverte: | |||
$ \frac{x^2}{2} = \frac 12 \cdot 6(6-x) \\ x^2+6x-36 = 0 \\ x= \frac{-6 \pm \sqrt{36+ 144}}{2}\\ x = \frac{-6 \pm \sqrt{180}}{2}\\ x= \frac{-6 \pm \sqrt{36 \cdot 5}}{2} \\ x= -3 \pm 3\sqrt3 $ | |||
Vi er bare interessert i den positive verdien, siden dette er lengden av et linjestykke: | |||
$x = 3 \sqrt5 -3$ | |||
Areal av hvit trekant blir: | |||
$A = 6^2 - 3 \cdot \frac 12 \cdot ( 3\sqrt5 - 3)^2= \\ 36- \frac 32 (45 -18 \sqrt 5 +9)= \\36-(81- 27 \sqrt 5) = \\ 27 \sqrt 5 - 45$ | |||
===Oppgave 3=== | ===Oppgave 3=== | ||
| Linje 204: | Linje 226: | ||
===b)=== | ===b)=== | ||
[[File:1t-h2015-23b.png]] | |||
Begge har stigningstall 2c-1, altså er de parallelle. | |||
===Oppgave 4=== | ===Oppgave 4=== | ||
[[File:1T-h2015-4.png]] | [[File:1T-h2015-4.png]] | ||
Lengde: $\frac 34$ | |||
Bredde: $\frac 12$ | |||
===Oppgave 5=== | ===Oppgave 5=== | ||
| Linje 213: | Linje 244: | ||
===a)=== | ===a)=== | ||
Antall kjøretøy i telleperioden: 1350 + 120 + 100 = 1570. | |||
Andel elbiler: $\frac{1350}{1570} =0,86$ | |||
Ja, det gir grunnlag for overskriften, men journalisten hadde hatt belegg for å skrive 9 av 10, noe som ville vært en enda større sensasjon. | |||
===b)=== | ===b)=== | ||
Binomisk fordeling: | |||
Elbil eller ikke elbil | |||
Kommer uavhengig av hverandre | |||
p= 0,8599 | |||
[[File:1T-h2015-25b.png]] | |||
Det er 5% sannsynlig at det er nøyaktig en elbil, av tre kjøretøy, som passerer. | |||
===c)=== | ===c)=== | ||
[[File:1T-h2015-25c.png]] | |||
Det er ca 95% sannsynlig at to eller tre biler som passerer er elbiler. | |||
===Oppgave 6=== | ===Oppgave 6=== | ||
| Linje 222: | Linje 274: | ||
===a)=== | ===a)=== | ||
Bruker Cosinussetningen: | |||
$6^2= 8^2 + (AB)^2 - 2 \cdot 8 \cdot AB \cdot Cos (45^{\circ})$ | |||
[[File:1T-h2015-26a.png]] | |||
Begge løsninger er mulige. | |||
===b)=== | ===b)=== | ||
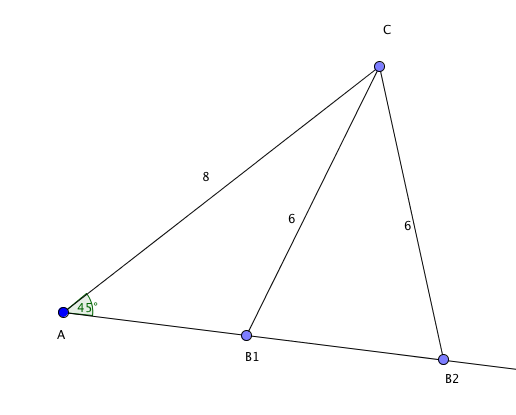
[[File:1T-h2015-26b.png]] | |||
Skisse av trekanten(e) i oppgave a. | |||
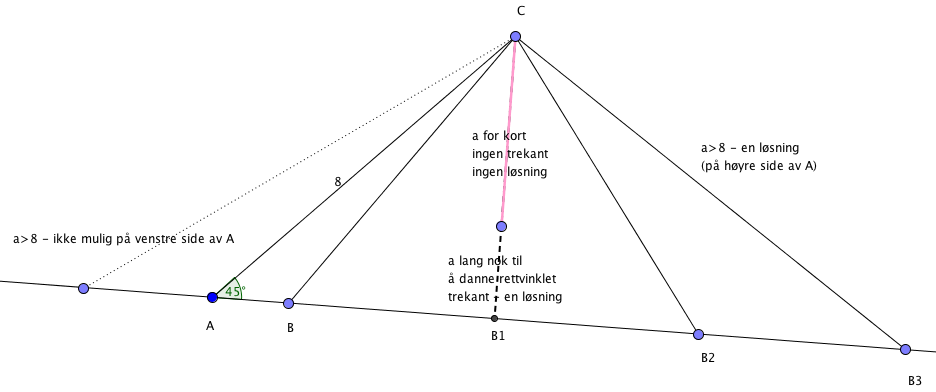
[[File:1T-h2015-26b2.png]] | |||
Generell skisse som viser ingen løsning, en løsning, og to løsninger. | |||
===c)=== | ===c)=== | ||
Vinkel A er 45 grader og AC = 8. Det betyr at største lengde BC kan ha er mindre enn 8, dersom to løsninger. En løsning har man dersom BC er større enn 8 og dersom BC har lengden som gjør at vinkel B er rettvinklet. Desom BC er kortere enn denne lengden har man ingen trekant, dvs. ingen løsning. | |||
[[File:1T-h2015-26c.png]] | |||
Den korteste lengden a kan ha er $a = 4 \sqrt2 \approx 5,66$. vi får da en rettvinklet trekant, altså bare en løsning. Trekanten er likebeint, dvs. at AB (x) er lik BC (a). | |||
Man tar ikke kvadratroten av negative tall (ikke her i alle fall) så: | |||
$a^2-32>0 \\ a^2 >32 \\ a> 4 \sqrt 2$ | |||
Det gir følgende: | |||
Ingen løsning: $a< 4 \sqrt2$ | |||
En løsning: $a= 4\sqrt2 \wedge a>8$ | |||
To løsninger: $4\sqrt 2 < a < 8$ | |||
===d)=== | ===d)=== | ||
Det stemmer. | |||
Siste sideversjon per 18. jan. 2016 kl. 04:19
DEL EN
Oppgave 1
$1,8 \cdot 10^{12} \cdot 0,0005 = \\ 1,8 \cdot 10^{12} \cdot 5 \cdot 10^{-4} = \\ 1,8 \cdot 5 \cdot 10^{12-4} = \\ 9,0 \cdot 10^{8}$
Oppgave 2
<math> \left[ \begin{align*}2x+3y = 13 \\ 4x-2y=2 \end{align*}\right] </math>
Ganger første likning med -2:
<math> \left[ \begin{align*}-4x-6y = -26 \\ 4x-2y=2 \end{align*}\right] </math>
Legger sammen likningene og x forsvinner:
<math> \left[ \begin{align*}-8y= -24 \end{align*}\right] </math>
Det gir y = 3. Innsatt i en av likningene gir det x = 2. Løsning er altså $x=2 \wedge y=3$
Oppgave 3
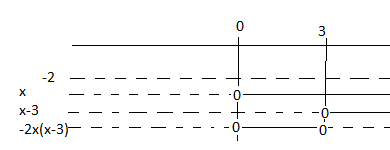
$-2x^2+6x<0 \\ -2x(x- 3)<0$
Fortegnsskjema:
$x \in < \leftarrow, 0> \cup < 3, \rightarrow>$
Oppgave 4
$( \sqrt 2 )^2+ \frac {\sqrt8}{2} +\sqrt[3]{8} - \frac{\sqrt[3]{128}}{\sqrt[3]{2}}= \\ 2 - \sqrt 2 + 2 - \frac{\sqrt[3]{2^7}}{\sqrt[3]{2}} = \\2 - \sqrt 2 + 2 - \frac{4\sqrt[3]{2}}{\sqrt[3]{2}} = \\ -\sqrt 2 $
Oppgave 5
$x^2+bx +c=0$ Løsninger $x_1= -4 \wedge x_2=2$
Setter inn for x:
$16-4b+c=0 \wedge 4+2b+c=0$
Multipliserer den siste med -1 og legger dem sammen:
12- 6b = 0 gir b = 2. Ved innsetting finner man c = -8
$x^2+2x - 8=0$
Oppgave 6
$\frac{x+1}{x-1} - \frac{x-3}{2x-2} + \frac 12 =\\ \frac{2x+2-x+3+x-1}{2(x-1)}=\\ \frac{2x+4}{2(x-1)} = \\ \frac{x+2}{x-1} $
Oppgave 7
$\frac{x^2-4xy+4y^2}{3xy- 6y^2} = \\\frac{(x-2y)^2}{3y(x-2y)} = \\ \frac{x-2y}{3y}$
Oppgave 8
$2^{4x} \cdot 2^{x^2} = 32 \\ 2^{x^2+4x} = 2^5 \\ x^2+4x-5=0 \\ x= \frac{-4 \pm \sqrt{16+20}}{2} = \\ x= -5 \vee x = 1$
Oppgave 9
Katetene er like lange. Lengde x:
$x^2 + x^2 = ( \sqrt2)^2 \\ 2x^2=2 \\ x =1$
Arealet blir da halvparten av en ganger en. A = 0,5
Oppgave 10
a)
$f(x)= x^2-x-2$
$f(x)=0 \\ x^2-x-2 =0 \\ x= \frac{1 \pm \sqrt{1+8}}{2} \\ x= -1 \vee x = 2$
Nullpunkter er (-1,0) og (2, 0)
b)
Koeffisienten foran andregradsleddet er positiv, det betyr at grafen vender sin hule side opp, og har et minimumspunkt. Dette ligger på symmetrilinja som er x= 0,5.
Eller vi kan derivere og sette den deriverte lik null:
$f'(x): 2x -1 \\f'(x)=0 \\ x = \frac 12$
$f( \frac 12) = \frac 14 - \frac 24 - \frac 84 = - \frac 94$
Dvs. bunnpunkt i $( \frac 12, - \frac 94)$.
c)
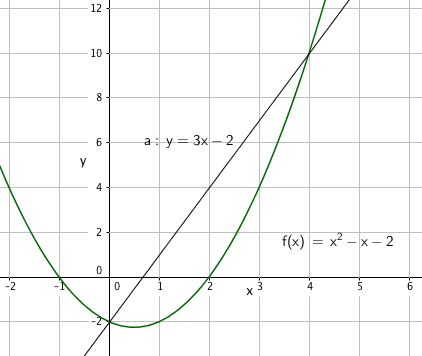
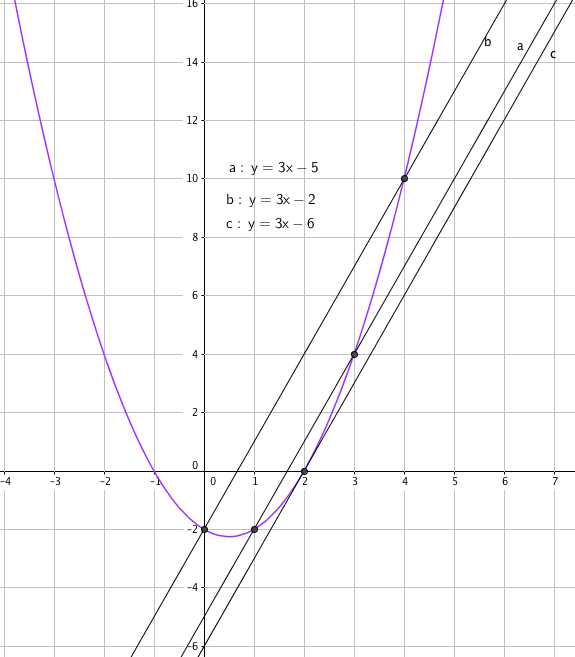
$y=ax+b \\ a = f´(2)= 3 \\ y =f(2) = 4-2-2=0 \\ y=ax+b \\ 0=3 \cdot 2 + b \Rightarrow b= -6 \\ y=3x-6 $
d)
Linje l: $y=ax+b \\7 = 3 \cdot 3 +b \Rightarrow b=-2 \\ y =3x-2$
Finner skjæring ved å sette uttrykkene lik hverandre:
$x^2-x-2=3x-2 \\ x^2-4x=0 \\ x(x-4)=0 \\ x=0 \vee x=4$
Finner y koordinatene:
$f(0)= -2 \wedge f(4) = 10$
Skjæringspunktene er (0, -2) og (4, 10).
e)
Oppgave 11
Formlikhet.
Dersom k er gjennomsnittet av lengdene til det parallelle sidene i det lille trapeset, er tilsvarende lengde i det store trapeset 3k.
Arealet av det lille trapeset er kh = A
Arealet av det store trapeset er $3k\cdot 3h = 9kh = 9A$
Oppgave 12
a)
| Smittet | Ikke smittet | sum | |
| Tester positivt | 58 | 10 | 68 |
| Tester ikke positivt | 2 | 290 | 292 |
| sum | 60 | 300 | 360 |
b)
P( pos | smittet) = $\frac{58}{60} = \frac{29}{30}$
c)
P( ikke smittet | pos test) = $\frac{10}{68} = \frac{5}{34}$
Oppgave 13
Finner først hypotenusen:
$b = \sqrt{12^2+5^2} = 13 \\ cos C = \frac{5}{13} $
Oppgave 14
Nedfeller normalen Fra C på AB. Det er høyden h i trekanten ABC. Kaller punktet normalen treffer AB på for D.
$Sin B = \frac{h}{20} \\ \frac{3}{5} = \frac{h}{20} \\ h = 12$
Bruker Pytagoras to ganger, for å finne grunnlinja AB:
AB = AD + DB = $\sqrt{13^2 - 12^2} + \sqrt{20^2-12^2} = 5+16= 21$
Areal: $A= \frac{21 \cdot 12}{2} = 126$
DEL TO
Oppgave 1
a)
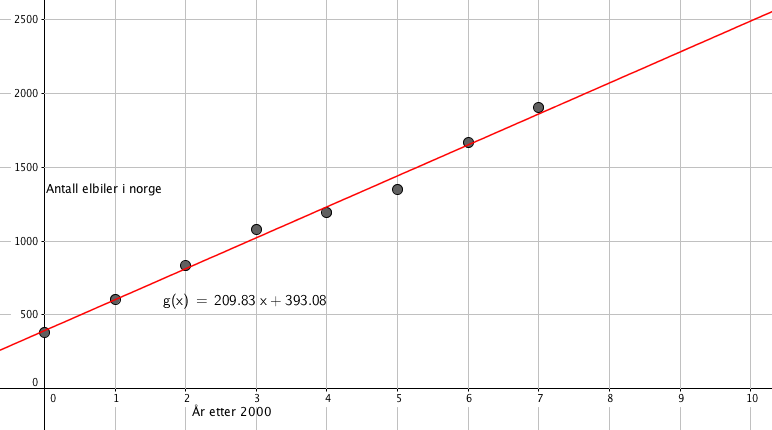
I de første åtte årene beskrives salget godt av den lineære funksjonen y = 210x + 393
b)
Allerede i 2008 underestimerer modellen betydelig. Etter hvert blir det verre da utviklingen synes eksponentiell. Modellen i a passer ikke til å si noen om fremtidig utvikling.
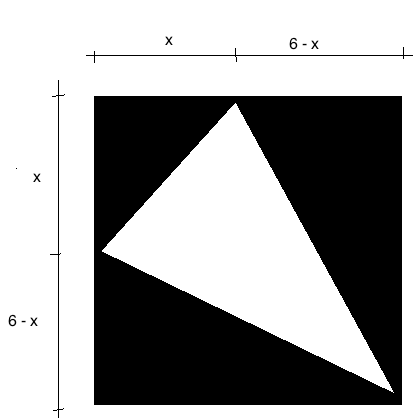
Oppgave 2
De tre skraverte trekantene har samme areal (selv om det ikke ser slik ut :-))
Setter arealet av den likebeinte skraverte trekanten lik arealet til en av de andre skraverte:
$ \frac{x^2}{2} = \frac 12 \cdot 6(6-x) \\ x^2+6x-36 = 0 \\ x= \frac{-6 \pm \sqrt{36+ 144}}{2}\\ x = \frac{-6 \pm \sqrt{180}}{2}\\ x= \frac{-6 \pm \sqrt{36 \cdot 5}}{2} \\ x= -3 \pm 3\sqrt3 $
Vi er bare interessert i den positive verdien, siden dette er lengden av et linjestykke:
$x = 3 \sqrt5 -3$
Areal av hvit trekant blir:
$A = 6^2 - 3 \cdot \frac 12 \cdot ( 3\sqrt5 - 3)^2= \\ 36- \frac 32 (45 -18 \sqrt 5 +9)= \\36-(81- 27 \sqrt 5) = \\ 27 \sqrt 5 - 45$
Oppgave 3
a)
b)
Begge har stigningstall 2c-1, altså er de parallelle.
Oppgave 4
Lengde: $\frac 34$
Bredde: $\frac 12$
Oppgave 5
a)
Antall kjøretøy i telleperioden: 1350 + 120 + 100 = 1570.
Andel elbiler: $\frac{1350}{1570} =0,86$
Ja, det gir grunnlag for overskriften, men journalisten hadde hatt belegg for å skrive 9 av 10, noe som ville vært en enda større sensasjon.
b)
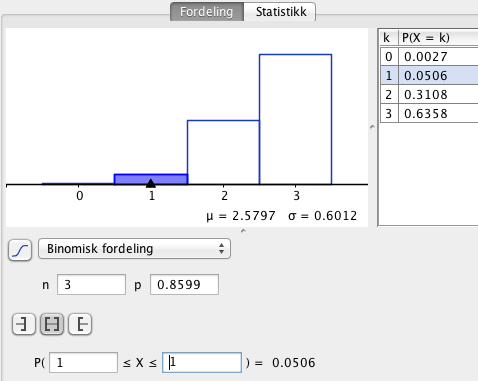
Binomisk fordeling:
Elbil eller ikke elbil
Kommer uavhengig av hverandre
p= 0,8599
Det er 5% sannsynlig at det er nøyaktig en elbil, av tre kjøretøy, som passerer.
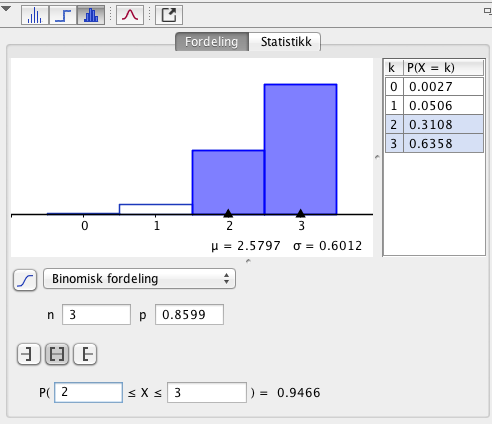
c)
Det er ca 95% sannsynlig at to eller tre biler som passerer er elbiler.
Oppgave 6
a)
Bruker Cosinussetningen:
$6^2= 8^2 + (AB)^2 - 2 \cdot 8 \cdot AB \cdot Cos (45^{\circ})$
Begge løsninger er mulige.
b)
Skisse av trekanten(e) i oppgave a.
Generell skisse som viser ingen løsning, en løsning, og to løsninger.
c)
Vinkel A er 45 grader og AC = 8. Det betyr at største lengde BC kan ha er mindre enn 8, dersom to løsninger. En løsning har man dersom BC er større enn 8 og dersom BC har lengden som gjør at vinkel B er rettvinklet. Desom BC er kortere enn denne lengden har man ingen trekant, dvs. ingen løsning.
Den korteste lengden a kan ha er $a = 4 \sqrt2 \approx 5,66$. vi får da en rettvinklet trekant, altså bare en løsning. Trekanten er likebeint, dvs. at AB (x) er lik BC (a).
Man tar ikke kvadratroten av negative tall (ikke her i alle fall) så:
$a^2-32>0 \\ a^2 >32 \\ a> 4 \sqrt 2$
Det gir følgende:
Ingen løsning: $a< 4 \sqrt2$
En løsning: $a= 4\sqrt2 \wedge a>8$
To løsninger: $4\sqrt 2 < a < 8$
d)
Det stemmer.