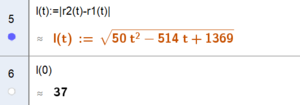R1 2024 Høst LØSNING

DEL EN

Oppgave 1

$f(x) = \frac{e^{2x}}{x}$

Deriverer f: $f'(x) = \frac{(e^{2x})' \cdot x + x' \cdot e^{2x}}{x^2} = \frac{2xe^{2x} + e^{2x}}{x^2} = \frac{e^{2x} (2x + 1)}{x^2} $

Oppgave 2

Programmet leter etter toppunktet til funksjonen $O(x) = -0,1x^2+2000x-50000$.

Programmet løper gjennom en while løkke og sjekker funksjonsverdien O(x+1) i forhold til O(x). Så lenge O(x+1)> O(x) fortsetter løkken. Når det ikke lenger er tilfellet, skriver det ut x- verdien.

Vi deriver O og setter uttrykket lik null.

$-0,2x + 2000 =0$

$x = \frac{-2000}{-0,2} = 10000 $

Programmet skriver ut 10000, som er x verdien som gir størst funksjonsverdi.

Oppgave 3

$100 ^x - 3 \cdot 10^x= 4$

$ (10^2)^x - 3 \cdot 10^x-4 =0$

$(10^x)^2 - 3 \cdot 10^x- 4 = 0$

$10^x = \frac{3 \pm \sqrt{9+16}}{2}$

$10^x = \frac{3 \pm 5}{2}$

Vi er bare interessert i den positive verdien fordi vi ikke kan opphøye 10 i noe som gir en negativ verdi.

$10^x = 4$

$x = lg(4)$

Oppgave 4

\[ \lim_{x\to \infty} \frac{x^2+x-12}{2x^2 -18} \]

\[ \lim_{x\to \infty} \frac{\frac{x^2}{x^2}+ \frac{x}{x^2}- \frac{12}{x^2}}{ \frac{2x^2}{x^2} - \frac{18}{x^2}} \]

\[ \lim_{x\to \infty} \frac{1 + \frac{1}{x}- \frac{12}{x^2}}{ 2 - \frac{18}{x^2}} = \frac 12 \]

Oppgave 5

a)

Lengden av vektorene avgjøres av koordinatenes avstand fra origo. x og y koordinatene er katetene i en trekant der hypotenusen er selve vektoren. For lengden del er vi bare interessert i absoluttverdien og ser da at u og w vektor er like lange, altså $| \vec{u}| = | \vec {w}|$.

Ortogonale er et annet ord for vinkelrett på hverandre. Da er skalarproduktet lik null.

$\vec{u} \cdot \vec{p} = (3 \cdot 8) + ((-2) \cdot 12) = 24-24 =0$

Disse to er det eneste som står vinkelrett på hverandre. Alle andre skalarprodukter her er forskjellig fra null, og da har man ikke ortogonalitet.

b)

$\vec{u} + 2 \vec{q} =[7,5]$

$[3,-2] + 2[2a - 3, 1 + 3b] = [7,5]$

$[3+4a-6, -2 + 2 + 6b] = [7, 5]$

$4a - 3 = 7 \wedge 6b = 5$

$a= \frac 52 \wedge b = \frac 56 $

Oppgave 6

Både g og f tilfredsstiller kravet om gjennomsnittlig vekstfart i intervallet [0,4]. g har derivert lik 0,5 for alle x, så det er kun f som tilfredsstiller kravene.

DEL TO

Oppgave 1

a)

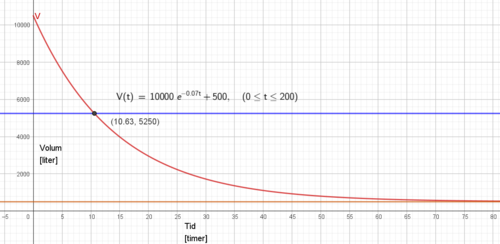
Vannmengden er halvert etter 10 timer og 38 minutter.

b)

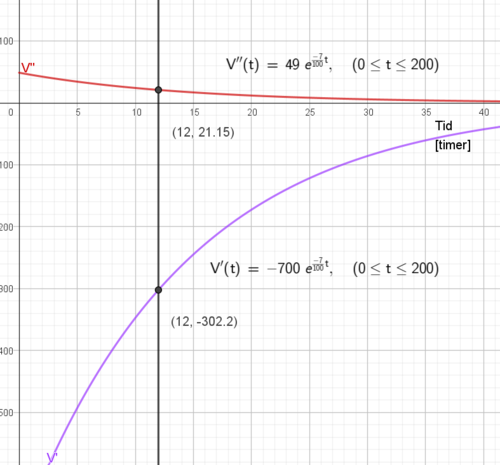
Den 12 timen reduseres vannmengden med ca 302 liter. Lekkasjen blir ca. 21 liter mindre i løpet av denne timen.

Vi ser at den deriverte av V er negativ. Det betyr at V minker. Den dobbeltderiverte av V, eller den deriverte av den deriverte, er positiv. Det betyr at den negative verdien til V derivert blir mindre negativ, altså at lekkasjen blir mindre.

c)

Fra figuren i a ser man at vannmengden nærmer seg 500 liter når tiden blir høy, så y = 500 er en horisontal asymptote.

En praktisk tolkning kan være at lekkasjen ikke er helt i bunnen, men et lite stykke oppe på reservoarveggen, slik at de 500 literne aldri renner ut.

Oppgave 2

a)

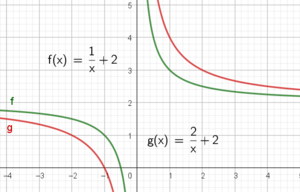
Begge går mot samme grenseverdi når x går mot pluss eller minus uendelig. Påstanden er feil.

b)

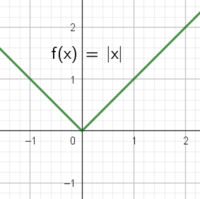
Det er riktig. Funksjonen er ikke deriverbar for X = 0.

Grafen har et knekkpunkt for x = 0 og er ikke deriverbar i dette punktet.

c)

Påstanden er feil for $a \in \mathbb{R}$

$a \in \mathbb{R} \setminus \left\{ -1, 0, 1 \right\}$ så er x = y.

a= - 1 gir løsninger når både x og y er partall, eller når begge er oddetall

$a = 0 \vee a = 1 $ er $x \neq y$ løsninger, såvel som $x = y$

Oppgave 3

a)

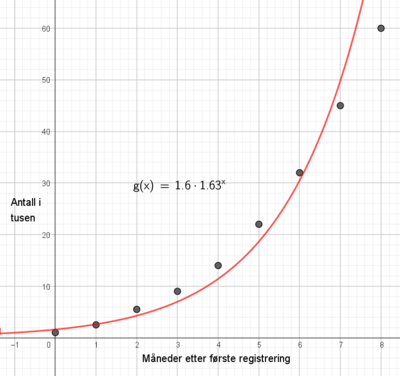
Modellen foreslår 1,6 tusen = 1600 fisk som startverdi, og en vekst på 63% per måned.

b)

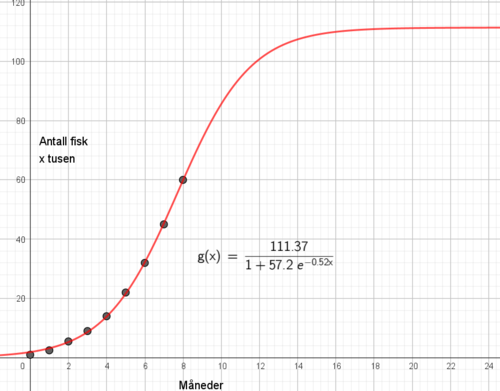
Bæreevne: B = 111 370 fisk

Vekstparameter: r = 0,52

For å finne hva modellen bruker som startverdi løser v i

$ \frac {111,37 - N_0}{N_0} = 57,2$

Det gir en startverdi på 1950 fisk.

c)

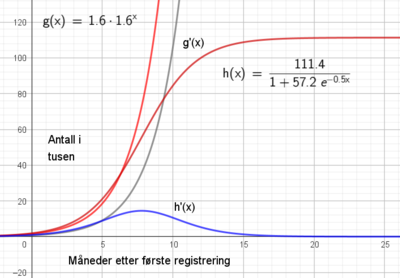
Den deriverte til g vokser i det uendelige, mens grafen til den logistiske modellen(h) har et vendepunkt etter 7- 8 måneder. Der deriverte blir mindre, veksten reduseres, for så å flate ut etter ca. 15 måneder.

d)

Den logistiske modellen er mest realistisk. Resursene er begrenset, i tette populasjoner kan sykdom opptre og enkelte individer blir også mat for andre i næringsnettet. Etter 12 mnd. er det ca. 100 000 individer.

Oppgave 4

Logaritmen til basisen for logaritmen er 1. Eksempelvis er $lg_{10}(10) = 1 $ og $ln(e) =1$. Derfor er basis her 5.

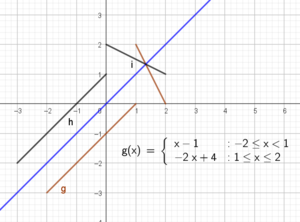
(Hvilket tall gir deg 25 dersom du opphøyer det i andre? Fra figur i oppgaven)

Oppgave 5

a)

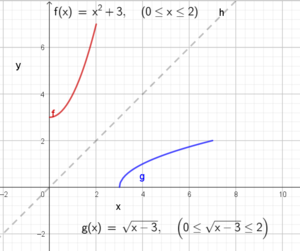
Dersom en hvilket som helst rett linje parallell med x aksen skjærer grafen i ett og bare ett punkt, er den en-entydig og kan ha en omvendt funksjon. Vi ser at h ikke oppfyller kravet. f og g har omvendte funksjoner, men ikke h.

b)

Den første funksjonen ser ut til å kunne være en andregradsfunksjon. Den skjærer y aksen i 3 og øker så med 1 når x=1 og med 4 når x=2. Det passer med funksjonen

$ f(x) = x^2 + 3 $

$y= x*2 +3$

$x^2 = y-3$

$x = \pm \sqrt{y-3}$