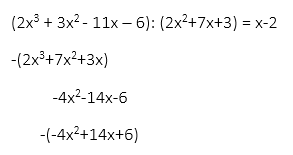Forskjell mellom versjoner av «1T 2024 vår LK20 LØSNING»
| (22 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 7: | Linje 7: | ||
=Del 1= | =Del 1= | ||
==Oppgave 1== | ==Oppgave 1== | ||
| − | |||
| − | |||
| − | $\frac{6}{8} | + | ===a)=== |
| + | Tangens til vinkelen er definert som motstående katet, delt på hosliggende katet. | ||
| + | |||
| + | $\tan(u) \cdot \tan(v) = \frac{6}{8} \cdot \frac{8}{6} = 1$ | ||
| − | |||
Dette betyr at Tom sin påstand er riktig. | Dette betyr at Tom sin påstand er riktig. | ||
| − | === | + | ===b)=== |
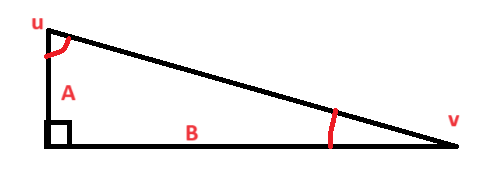
| − | I denne oppgaven skal vi avgjøre om påstanden stemmer for alle rettvinklete trekanter. | + | I denne oppgaven skal vi avgjøre om påstanden stemmer for alle rettvinklete trekanter. En generell rettvinklet trekant kan se slik ut: |
| + | |||
| + | [[File:05072024-01.png]] | ||
| + | |||
| + | |||
| + | $tan(u) \cdot tan(v) = \frac{B}{A} \cdot \frac{A}{B} = \frac{A}{A} \cdot \frac{B}{B} = 1$ | ||
| + | |||
| + | Påstanden stemmer for alle trekanter av den typen. | ||
==Oppgave 2== | ==Oppgave 2== | ||
| − | |||
| + | Dersom P(a) = 0, er P(x) delelig på (x-a) | ||
| + | |||
| + | $P(x) = 2x^3+3x^2-11x-6$ | ||
| + | |||
| + | P(0)=-6, P(-1)= 6, P(1)= -12, P(2)= 0. Vi ser også at $P(-3)= -54 + 27 + 33 -6= 0$ Vi observerer at polynomet skifter fortegn mellom P(0) og P(-1). Det kan derfor være fristende å teste om $x=- \frac{1}{2}$ er en rot i polynomet: $P(-\frac 12)= - \frac 14 + \frac 34 + 5,5 - 6 =0$ | ||
| + | |||
| + | Røttene er altså $x= -3, x= - \frac 12$ og x = 2. | ||
| + | |||
| + | Polynomet P er da delelig på (x+3), (x + 0,5) og (x-2) | ||
| + | |||
| + | Dersom man deler på (x-2): | ||
| + | |||
| + | |||
| + | [[File:05072024-02.png]] | ||
| + | |||
| + | Dersom man dividerer tredjegradspolynomet på andregradspolynomet bør man jo få (x-2) som resultat: | ||
| + | |||
| + | [[File:05072024-03.png]] | ||
| + | |||
| + | Dersom linje tre i oppgaven er riktig må det bety at andregradspolynomet kan faktoriseres. Vi tester: $2x^2+7x+3$ og ser (ved hjelp av koefisientmetoden) at $2x^2+7x+3 = 2((x+3)(x+ \frac 12))$ | ||
| + | |||
| + | |||
| + | $P(x) = 2x^3+3x^2-11x-6 = ( 2x^2+7x+3)(x-2) = 2(x-2)(x+ \frac 12)(x + 3)$ | ||
| + | |||
| + | Guri KAN ha utført de to divisjonene vist i oppgaven. Faktoriseringen hennes er riktig, men ikke fullstendig. | ||
| − | + | ==Oppgave 3== | |
| − | |||
| − | + | Stort kvadrat minus lite kvadrat: | |
| − | + | $a((a-b)+b) - (b\cdot b) = a \cdot a - b \cdot b = a^2-b^2$ | |
| − | + | Sum av stort rektangel pluss lite rektangel: | |
| − | + | $a(a-b) + b(a-b) = a^2-ab +ab - b^2 = a^2-b^2$ | |
| + | Ett eksempel på en identitet, med utgangspunkt i grønt areal er: $a(a-b) + b(a-b) = a^2 - b^2$ | ||
| − | |||
| − | + | ==Oppgave 4== | |
| − | + | ==Oppgave 5== | |
| − | + | Generelt: $f(x) = ax^2+bx+c$ | |
| − | + | Fra figuren leser vi at f(0) =24, dvs c=24 | |
| − | + | Videre har vi fra figuren at f(-3)= 0 og f(4)= 0 hvilket betyr at (x+3) og (x-4) er faktorer i funksjonen: $(x+3)(x-4) = x^2-x -12$ | |
| − | + | Vi ser fra konstantleddet c at vi må multiplisere med -2 for å få 24: | |
| − | + | $f(x) = -2(x^2-x-12)= -2x^2+2x+24$ | |
Revisjonen fra 5. jul. 2024 kl. 15:57
Diskusjon av oppgaven på matteprat
Løsning laget av Sindre Sogge Heggen
Del 1
Oppgave 1
a)
Tangens til vinkelen er definert som motstående katet, delt på hosliggende katet.
$\tan(u) \cdot \tan(v) = \frac{6}{8} \cdot \frac{8}{6} = 1$
Dette betyr at Tom sin påstand er riktig.
b)
I denne oppgaven skal vi avgjøre om påstanden stemmer for alle rettvinklete trekanter. En generell rettvinklet trekant kan se slik ut:
$tan(u) \cdot tan(v) = \frac{B}{A} \cdot \frac{A}{B} = \frac{A}{A} \cdot \frac{B}{B} = 1$
Påstanden stemmer for alle trekanter av den typen.
Oppgave 2
Dersom P(a) = 0, er P(x) delelig på (x-a)
$P(x) = 2x^3+3x^2-11x-6$
P(0)=-6, P(-1)= 6, P(1)= -12, P(2)= 0. Vi ser også at $P(-3)= -54 + 27 + 33 -6= 0$ Vi observerer at polynomet skifter fortegn mellom P(0) og P(-1). Det kan derfor være fristende å teste om $x=- \frac{1}{2}$ er en rot i polynomet: $P(-\frac 12)= - \frac 14 + \frac 34 + 5,5 - 6 =0$
Røttene er altså $x= -3, x= - \frac 12$ og x = 2.
Polynomet P er da delelig på (x+3), (x + 0,5) og (x-2)
Dersom man deler på (x-2):
Dersom man dividerer tredjegradspolynomet på andregradspolynomet bør man jo få (x-2) som resultat:
Dersom linje tre i oppgaven er riktig må det bety at andregradspolynomet kan faktoriseres. Vi tester: $2x^2+7x+3$ og ser (ved hjelp av koefisientmetoden) at $2x^2+7x+3 = 2((x+3)(x+ \frac 12))$
$P(x) = 2x^3+3x^2-11x-6 = ( 2x^2+7x+3)(x-2) = 2(x-2)(x+ \frac 12)(x + 3)$
Guri KAN ha utført de to divisjonene vist i oppgaven. Faktoriseringen hennes er riktig, men ikke fullstendig.
Oppgave 3
Stort kvadrat minus lite kvadrat:
$a((a-b)+b) - (b\cdot b) = a \cdot a - b \cdot b = a^2-b^2$
Sum av stort rektangel pluss lite rektangel:
$a(a-b) + b(a-b) = a^2-ab +ab - b^2 = a^2-b^2$
Ett eksempel på en identitet, med utgangspunkt i grønt areal er: $a(a-b) + b(a-b) = a^2 - b^2$
Oppgave 4
Oppgave 5
Generelt: $f(x) = ax^2+bx+c$
Fra figuren leser vi at f(0) =24, dvs c=24
Videre har vi fra figuren at f(-3)= 0 og f(4)= 0 hvilket betyr at (x+3) og (x-4) er faktorer i funksjonen: $(x+3)(x-4) = x^2-x -12$
Vi ser fra konstantleddet c at vi må multiplisere med -2 for å få 24:
$f(x) = -2(x^2-x-12)= -2x^2+2x+24$