Sirkellikningen

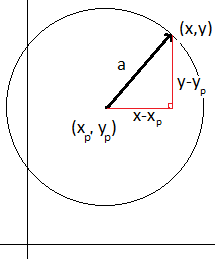
Et punkt P har koordinatene <math>(x_p,y_p)</math>. en vektor har lengden a, og en vilkårlig rettning. Vektoren ender i punktet S som har koordinatene (x,y). Dersom man holder vektoren fast i P og varierer rettningen ser man at S vil spore en sirkel med radius a og med sentrum i P.

Ved å anvende Pytagoras får man:

<math> (x-x_p)^2 + (y-y_p)^2 = a^2</math>

Vektorregning gir:

<math> \vec{PS} = [x-x_p , y-y_p]</math>

Lengden av PS vektor er

<math> |\vec{PS}| = \sqrt{(x-x_p)^2 +(y-y_p)^2} = a \\(\sqrt{(x-x_p)^2 +(y-y_p)^2})^2 = a^2 \\

(x-x_p)^2 +(y-y_p)^2 = a^2 </math>

Som er likningen for en sirkel med radius a og sentrum i <math>(x_p,y_p)</math>