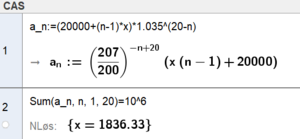S2 2023 høst LØSNING
DEL EN
Oppgave 1
$\int_{-1}^{1}(x^3+2x) dx = [\frac 14 x^4 + x^2]_{-1}^{1} = (\frac 14 +1) - ( \frac 14 +1) = 0$
Arealet avgrenset av grafen, x-aksen og linjen x=-1 er lik arealet avgrenset av linjen x =1. grafen og x-aksen. Den ene delen ligger under x-aksen, den andre over. Begge arealene er like store. Grafen går gjennom origo og vi har symmetri om origo.
Oppgave 2
a)
$S = \frac{a_1}{1-k}$
Siden rekken konverger mot 8 må k være $\frac 12 $ :
$8 = \frac{4}{1-k} \Rightarrow k= \frac 12$
$S_4 = 4+2+1+ \frac 12 = 7,5$
b)
I en aritmetisk rekke øker leddene med en fast verdi d.
$a_1 = a_4 - 3d $
$a_7 = a_4 + 3d$
$a_1 + a_4 + a_7 = 114$
$a_4 -3d + a_4 + a_4 +3d =114$
$3 a_4 = 114$
$a_4 = 38$
Oppgave 3
a)
Stigningstallet til en rett linje gjennom origo skjærer kostnadsfunksjonen i x = a. Stigningstallet gir oss enhetskostnaden ved produksjon av a enheter. I dette tilfellet har linjen som skjærer kostnadsfunksjonen i x = 40 stigningstall 81,75 kr. og er altså enhetskostnaden ved produksjon av 40 enheter.
b)
Grensekostnaden er sånn ca. hva det koster å øke produksjonen med en enhet, altså den deriverte i punktet. For 40 enheter ser man at stigningstallet til tangenten, den deriverte, er 31 kroner.
c)
Stigningstallet til den rette linjen som går gjennom origo og samtidig tangerer kostnadsfunksjonen gir den laveste enhetskostnaden, i dette tilfelle 60 kroner.
Oppgave 4
a)
Programmet regner ut arealet av flaten som er avgrenset av f(x), x- aksen, linjen x = -2 og linjen x = 2.
b)
$f(x) = x^2-1$
Funksjonen har nullpunkter for x=-1 og x= 1. Mellom disse ligger den under x aksen. Den er symmetrisk om y-aksen. Vi integrerer fra -2 til -1 og fra -1 til 0. Til slutt multipliserer vi med 2, for å finne hele arealet.
$A= 2 \cdot ( \int_{-2}^{-1}(x^2-1)dx +| \int_{-1}^{-0}(x^2-1))dx | $
$ = 2 \cdot ( [\frac 13 x^3- x ]_{-2}^{-1} + | [ \frac 13 x^3 - x]_{-1}^{0}) | $
$= 2 \cdot ( (\frac {-1}{3}+1) -( \frac {-8}{3} +2) + | ((0)- (\frac{-1}{3} + 1) |$
$ = 2 \cdot ( \frac 43 + \frac 23) $
$ = 2 \cdot \frac 63 $
$= 4$
Oppgave 5
a)
Forventningsverdi 𝐸(𝑋)
Siden den totale sannsynligheten må være 1, kan vi finne sannsynligheten for å trekke en kule som veier 10 kg:
$P(X=10)=1−P(X=4)−P(X=5)=1− \frac 14 - \frac 12= \frac 14$
$E(x) = \sum_i x_i \cdot P(X=x_i) = 10 \cdot \frac 14 + 5 \cdot \frac 12 + 4 \cdot \frac 14 = 2,5 + 2,5 + 1 = 6$
E(X) er 6 kg.
Varians, Var(x):
$Var(X) = E(X^2)-(E(X))^2$
$Var(X) = \sum_i x_i^2 \cdot P(X=x_i) - \mu^2$
$Var(X) =( 4^2 \cdot \frac 14 + 5^2 \cdot \frac 12 + 10^2 \cdot \frac 14) - 6^2$
$Var (x) = \frac{16}{4} + \frac{25}{2} + \frac{100}{4} -36 = 41,5 -36 = 5,5$
b)
Y er summen av vekten til to kuler.
Vi trekker en kule to ganger (med tilbakelegging), så vi må finne sannsynlighetene for summen av vektene til de to kulene. La $X_1$ og $X_2$ være vektene av de to kulene. De mulige verdiene av $𝑌 = X_1 + X_2$
Mulige Y verdier er:
$4+4= 8, \quad 4+5 = 9, \quad 4+10 = 14 $
$5+4= 9, \quad 5+5 = 10, \quad 5+10 = 15 $
$10+4= 14, \quad 10+5 = 15, \quad 10+10 = 20 $
$P(Y=8) = \frac 14 \cdot \frac 14 = \frac {1}{16}$
$P(Y=9) = \frac 14 \cdot \frac 12 + \frac 12 \cdot \frac 14 = \frac {1}{4}$
$P(Y=10) = \frac 12 \cdot \frac 12 = \frac {1}{4}$
$P(Y=14) = \frac 14 \cdot \frac 14 + \frac 14 \cdot \frac 14 = \frac {1}{8}$
$P(Y=15) = \frac 12 \cdot \frac 14 + \frac 14 \cdot \frac 12 = \frac {1}{4}$
$P(Y=20) = \frac 14 \cdot \frac 14 = \frac {1}{16}$
c)
$P(Y> 10)$
Vi summerer resultatene fra b som er større enn 10:
$P(Y=14)+ P(Y=15)+ P(Y=20) = \frac {1}{8} + \frac {1}{4} + \frac {1}{16} = \frac{7}{16}$
Sannsynligheten for at Y er større enn 10 er $ \frac {7}{16}$
DEL TO
Oppgave 1
a)
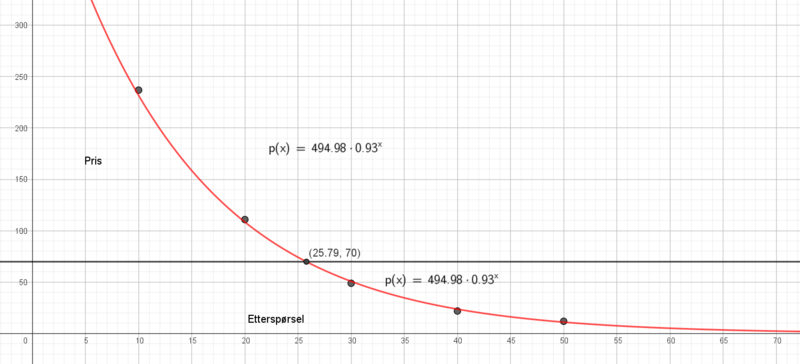
Har brukt eksponentiell regresjon. Generelt er slike modeller relativt gode mellom og nær målepunkter, men ikke nødvendigvis gode til forutse utviklinger. Er noen kunder avhengig av dette produktet? Er det mange lignende produkter i markedet? Kommer det politiske pålegg i nær framtid som kan påvirke markedet? Disse og mange andre spørsmål tar ikke regresjonen høyde for. Når det er sagt ser jo modellen lite kontroversiell ut, så det kan god være den har en viss gyldighet for alle mulige positive priser. p > 0.
b)
For å selge 70 enheter per dag bør prisen være 26 kroner (25,79).
c)
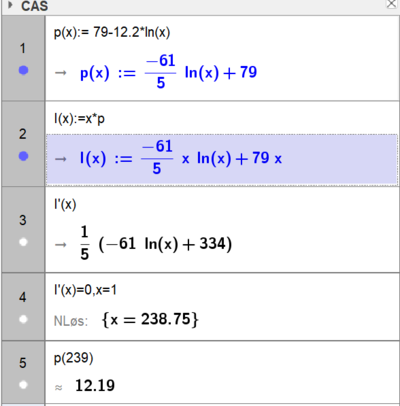
For at inntektene skal bli størst mulig må prisen være ca.12,19 kr. Da er etterspørselen ca. 239 enheter.
d)
Man bør selge 80 enheter daglig, for å maksimere overskuddet.
Oppgave 2
Miriam har bestemt seg for å sette inn 20 000 kroner på en konto i begynnelsen av hvert år. Det første sparebeløpet vil hun sette inn i begynnelsen av 2024, det andre beløpet i begynnelsen av 2025, og så videre. Anta at hun får en fast årlig rentesats på 3,5 prosent.
a)
Vis at Miriam vil ha 565 594 kroner på kontoen like etter at hun har satt inn innskudd nummer 20.
Løsn.
Vi skal finne sluttbeløpet når vi kjenner innskuddsbeløp og rente.
Dette er en rekke med 20 ledd der $a_1 = 20000$ og k = 1,035
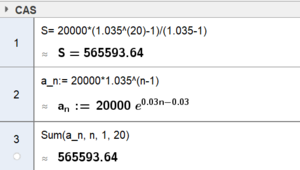
Sum: $S_{20}=20000\frac{1,035^{20}-1}{1,035-1} = 565594$
På Geogebra på to måter:
Hermod har også bestemt seg for å spare. Han vil sette inn et fast beløp i
begynnelsen av hvert år. Det første sparebeløpet setter han inn i begynnelsen av
2024. Han får også en fast årlig rentesats på 3,5 prosent. Hermod har regnet ut
at han vil ha 692 852 kroner på kontoen like etter at innskudd nummer 20 er satt
inn.
b)
Bestem beløpet Hermod må sette inn hvert år for at dette skal stemme.
Løsn.
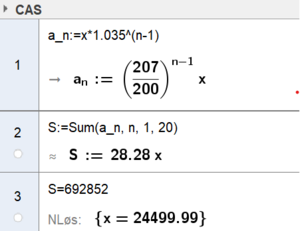
Vi skal finne innskuddsbeløp når vi kjenner sluttbeløp og rente. Vi har fortsatt en geometrisk rekke, med $a_1 = x$ og $k= 1,035$. Vi bruker Geogebra:
Han må spare 24500 kr. hvert år.
Miriam ønsker at det skal være 1 000 000 kroner på kontoen like etter at hun har satt inn innskudd nummer 20. For å få til dette, vil hun øke innskuddet med et fast beløp hvert år. Første innskudd skal være 20 000 kroner.
c)
Hvor mye må hun øke innskuddet med hvert år?
Løsn:
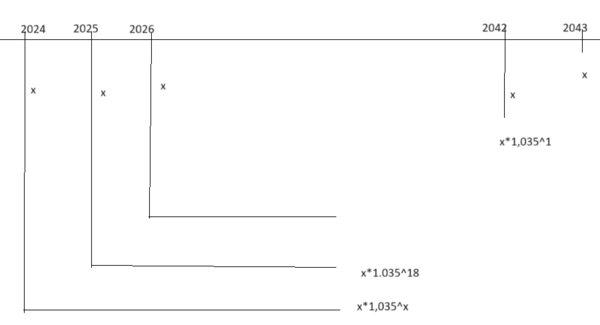
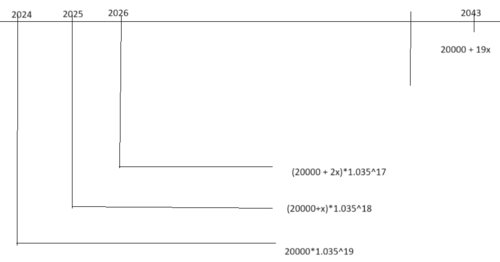
Vi har følgende situasjon:
Dette er en rekke der $a_n = (20000+(n-1)x)\cdot 1.035^{20-n}$
Vi løser med Geogebra:
Hun må årlige øke beløpet med 1836,33 kr.
Oppgave 3
Oppgave 4
a)
$a_n = a_{(n-1)}+ 5(-1)n$
b)
Oppgave 5
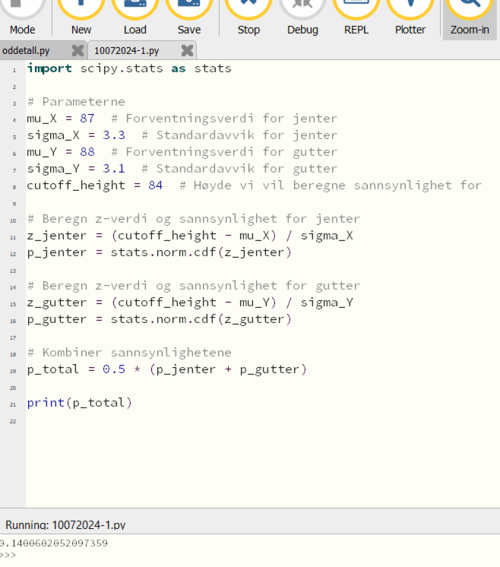
Eksempel på program som simulerer antall barn med høyden lavere enn 84 cm. på 24 måneder gamle barn.
Sannsynligheten for at et tilfeldig barn på 24 måneder er lavere enn 84 cm er ca 14%.